Neste primeiro momento, estudaremos as representações dos vetores em um espaço de até 3 dimensões (tridimensional). Além disso, veremos duas representações para os vetores, a geométrica e a algébrica. Aprenderemos, também, a realizar operações básicas entre vetores e multiplicação por escalar, o processo de normalização e verificação de igualdade entre vetores.

Tratamento Geométrico

Vetor é um segmento de reta orientado que apresenta módulo (tamanho), direção e sentido. Os vetores são usados para expressar grandezas físicas vetoriais, isto é, aquelas que são definidas pelo seu valor numérico, sua direção (horizontal e vertical), e também pelo seu sentido (para cima ou para baixo).

A representação gráfica de um vetor é dada por uma seta, e possui em suas extremidades dois pontos que o determinam (WINTERLE, 2000). Intuitivamente, seta é um segmento no qual se fixou uma orientação. E fixar uma orientação é escolher um sentido. No caso da Figura 1.1, o segmento orientado representado tem orientação de A para B.

As notações matemáticas para um vetor podem ser as mais diversas, dependendo do autor, as mais usuais são \(AB\), os dois pontos que deram origem ao vetor seguido de uma flecha sobre eles \(\overrightarrow{AB}\), uma letra minúscula seguida de uma flecha \(\vec{v}\) , uma letra minúscula em negrito \(v\).

Para fins de padronização, utilizaremos \(v\) como representação de um vetor.

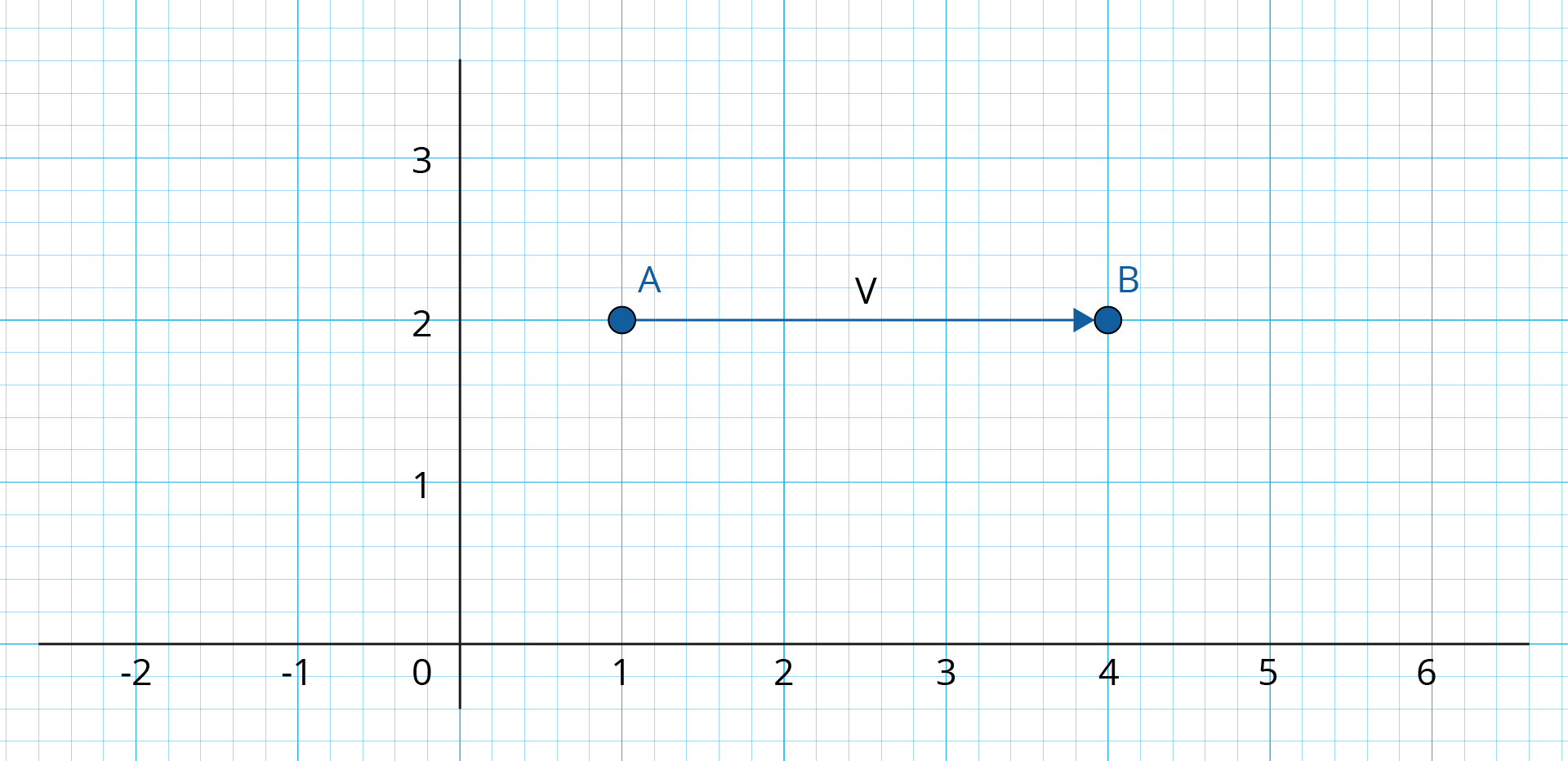
O módulo de um vetor é o comprimento dele, por exemplo, na figura 1.3 a seguir temos um vetor \(v\) com origem em (1,2) e final em (4,2). O módulo será a distância do ponto de origem até o ponto de destino. Verificamos pela figura 1.3 que o comprimento do vetor \(v\) é 3. A direção é o sentido que representamos quando desenhamos o vetor em um plano cartesiano. Observamos pela figura 1.3 que o vetor \(v\) possui direção horizontal e sentido da esquerda para direita.

O vetor que possui sua origem coincidindo com a sua extremidade é chamado vetor nulo denotado por 0 . Note que o vetor nulo é apenas um ponto no espaço.

Exemplo 1: Dados dois vetores AB e CD , dizemos que AB é equivalente a CD se B-A=D-C. Para verificarmos essa situação considere os seguintes pontos no plano:

a)  \(A=\left( 0,0 \right),~B=\left( 2,3 \right),~C=\left( 1,2 \right),~D=\left( 1,1 \right),~E=\left( 1,0 \right)~,~F=\left( -1,-1 \right).\)

Então, AD é equivalente a CB , pois

b)  \(D-A=\left( 1,1 \right)-\left( 0,0 \right)=\left( 1,1 \right)\)

c)  \(B-C=\left( 2,3 \right)-\left( 1,2 \right)=\left( 1,1 \right).\)

Contudo, podemos verificar que o vetor FE , \(E-F=\left( 1,0 \right)-\left( -1,-1 \right)=\left( 2,1 \right),\) não é equivalente a AD e CB . Os vetores AD , CB e FE são representados na figura 1.4.

Observação: A equivalência de vetores é análoga ao que ocorre com os números racionais e as frações. Duas frações representam o mesmo número racional se o numerador e o denominador de cada uma delas estiverem na mesma proporção. Por exemplo, ½ é equivalente a 2/4 e 3/6, e representam o mesmo número racional.

Operações com Vetores

Nesta seção iremos apresentar as seguintes operações vetoriais: Adição de vetores e produto de um escalar por um vetor.

Adição de Vetores

Consideremos os vetores \(u\) e \(v\), cuja soma \(u+v\) pretendemos encontrar. Para isso, tomemos um ponto A qualquer e, com origem nele, tracemos o segmento orientado AB representante do vetor \(u\). A partir de A, tracemos o segmento orientado AC representante de \(v\). O vetor representado pelo segmento orientado de origem A e extremidade D é, por definição, o vetor soma de \(u\) por \(v\). Essa regra é conhecida como regra do Paralelogramo.

Observe que a soma  \(u+v\) está na diagonal do paralelogramo determinado por \(u\) e \(v\), quando estão representados com a mesma origem.

Sendo \(u,~v\) e \(w\) vetores quaisquer, a adição admite as seguintes propriedades:

i)   Comutativa: \(u+v~=~v+u\)

ii)   Associativa: \(\left( u+v \right)+w~=~u+\left( v+w \right)\)

iii)  Elemento neutro: \(u+0~=~u\)

iv)  Elemento oposto: \(u+\left( -u \right)=0\)

O vetor \(u+(-v)\) , escreve-se \(u-v\), e é chamado de diferença entre \(u\) e \(v\).

Multiplicação por Escalar

A multiplicação de um vetor \(v~\ne ~0\) por um escalar e um escalar \(\alpha ~\ne ~0\), chama-se produto do número real 𝛂 pelo vetor \(v\), o vetor \(\alpha v\) tal que

A Figura 1.6 apresenta o vetor \(v\) e alguns de seus múltiplos.

Sejam os vetores \(u\) e \(v\) e \(\alpha \) e \(\beta \) escalares. São válidas as seguintes propriedades:

• \(\alpha \left( u+v \right)~=~\alpha u~+~\alpha v;\)
• \(\left( \alpha \beta  \right)u~=~\alpha \left( \beta u \right);\)
• \(\left( \alpha +\beta  \right)u~=~\alpha u~+~\beta u;\)
• \(1.u~=~u.\)

Tratamento Algébrico

As operações com vetores podem ser definidas utilizando um sistema de coordenadas cartesianas. Primeiramente, vamos considerar os vetores no plano.

Seja v um vetor no plano \({{R}^{2}}\). Definimos as componentes de \(v\) como sendo as coordenadas \(\left( {{v}_{1}},{{v}_{2}} \right)\) do ponto final do representante de \(v\) que tem ponto inicial na origem.

Identificamos o vetor com as suas componentes e vamos escrever simplesmente

\[v=\left( {{v}_{1}},{{v}_{2}} \right)\]

Em termos das componentes podemos realizar as operações: adição e multiplicação por escalar.

1. A adição de dois vetores \(u=\left( {{u}_{1}},{{u}_{2}} \right)\) e \(v=\left( {{v}_{1}},{{v}_{2}} \right)\) é dada por
   \[u+v~=\left( {{u}_{1}}+{{v}_{1}},~{{u}_{2}}+{{v}_{2}} \right)\]
2. A multiplicação de um vetor \(v=\left( {{v}_{1}},{{v}_{2}} \right)\) por um escalar 𝛂 é dada por
   \[\alpha v=(\alpha {{v}_{1}},\alpha {{v}_{2}})\]

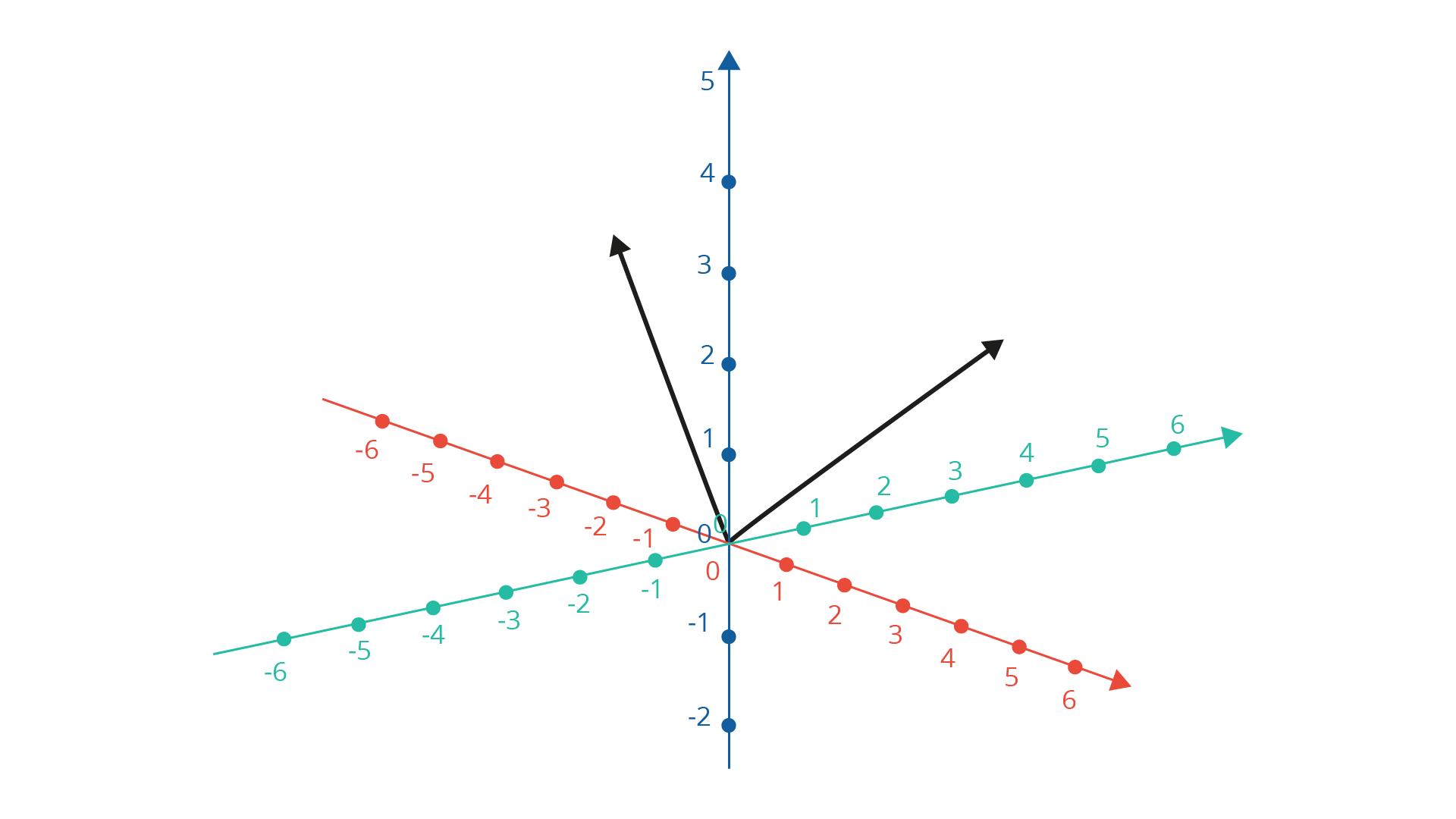
Analogamente, definimos a adição e multiplicação por escalar de um vetor v no espaço R3 (no caso os vetores têm 3 coordenadas como mostrado na figura 1.8. Como no caso de vetores no plano, definimos as componentes de \(v\) como sendo as coordenadas \(v=({{v}_{1}},{{v}_{2}},{{v}_{3}})\)

• Se \(u=({{u}_{1}},{{u}_{2}},{{u}_{3}})\) e \(v=({{v}_{1}},{{v}_{2}},{{v}_{3}})\), então a adição é definida como
  \[u+v=({{u}_{1}}+{{v}_{1}},{{u}_{2}}+{{v}_{2}},{{u}_{3}}+{{v}_{3}})\]
• Se  \(v=({{v}_{1}},{{v}_{2}},{{v}_{3}})\) e 𝛂 é um escalar, então a multiplicação por escalar é definida como
  \[\alpha v=(\alpha {{v}_{1}},\alpha {{v}_{2}},\alpha {{v}_{3}})\]

Exemplo 2: Se \(v=(2,3,0)\), \(w=(-5,0,3)\), então:

\[v+w=(2,3,0)+\left( -5,0,3 \right)=\left( 2+\left( -5 \right),3+0,0+3 \right)=\left( -3,3,3 \right)$\]

\[2v=\left( 2.\left( 2 \right),2.\left( 3 \right),2.\left( 0 \right) \right)=\left( 4,6,0 \right)\]

IGUALDADE - PARALELISMO - MÓDULO DE UM VETOR

As definições e conclusões no espaço são análogas às do plano:

I) Dois vetores \(u=\left( {{u}_{1}},{{u}_{2}},{{u}_{3}} \right)\) e \(v=\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right)\) são iguais se, e somente se, \({{u}_{1}}={{v}_{1}},~{{u}_{2}}={{v}_{2}},~{{u}_{3}}={{v}_{3}}\).

II) Se  \(u=\left( {{u}_{1}},{{u}_{2}},{{u}_{3}} \right)\) e \(v=\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right)\) são paralelos, então \(u~=~\alpha v\)  e representamos o paralelismo por \(u~//~v\).

III) O módulo do vetor \(v=\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right)\) é dado por \(\left| v \right| = \sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}+{{v}_{3}}^{2}}\).

A operação de módulo é realizada para a obtenção do valor do comprimento de um vetor \(v\).

Exemplo 3: Vamos determinar o módulo do vetor \(v~=\left( 4,3 \right)\)

Solução: O módulo de \(\left| v \right|=\sqrt{{{4}^{2}}+{{3}^{2}}}=\surd \left( 16+9 \right)=\surd 25=5\).

Ou seja, o comprimento do vetor \(v\) é de 5 unidades de comprimento. Observe na Figura a seguir que o comprimento do vetor \(v\) é calculado através do teorema de Pitágoras, o que justifica a fórmula do módulo de um vetor:

Devemos ficar atentos que o módulo do vetor sempre é um número positivo, pois indica um comprimento. Por exemplo, se os vetores têm componentes \(v=\left( -4,3 \right)\) o módulo continua sendo 5.

Vetores Unitários (versores)

Vetor é unitário quando seu módulo é igual a 1. Todo vetor que não seja unitário pode ser transformado em unitário por meio de um processo chamado de normalização, que é dada pela seguinte fórmula \(\hat{v}=v/\left| v \right|~\)

Existem vetores unitários especiais, que são \(\hat{i}=\left( 1,0,0 \right)\), \(\hat{j}=\left( 0,1,0 \right)\) e \(\hat{k}=\left( 0,0,1 \right)\).  Para o caso bidimensional, teremos apenas \(\hat{i}=\left( 1,0 \right)\), \(\hat{j}=\left( 0,1 \right)\). Qualquer vetor bidimensional ou tridimensional pode ser escrito como combinação linear desses vetores como mostrado nos exemplos abaixo:

\(\left( 2,3 \right)=2.\left( 1,0 \right)+3.\left( 0,1 \right)=2\hat{i}+3\hat{j}\) e

\(\left( 2,3,4 \right)=2.\left( 1,0,0 \right)+3.\left( 0,1,0 \right)+4.\left( 0,0,1 \right)=2\hat{i}+3\hat{j}+4\hat{k}\).

A utilização dos vetores unitários é de muita importância para a representação de vetores como mostraremos na próxima seção.

Vamos estudar, a partir de agora, as operações matemáticas de produto entre vetores. As operações que serão vistas são: produto escalar e produto vetorial. Em seguida, estudaremos as aplicações dessas operações, como na determinação de ângulo entre vetores, ortogonalidade e cálculo de área de paralelogramos.

Produto Escalar

Vamos definir, agora, um produto entre dois vetores, cujo resultado final é um escalar, por isso ele é chamado de produto escalar . Sejam \(u=\left( {{u}_{1}},{{u}_{2}},{{u}_{3}} \right)\) e \(v=\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right)\) dois vetores, o produto escalar entre \(u\) e \(v\), representado por \(u.v\) (lê-se \(u\) escalar \(v\)) é definido como

\[u.v={{u}_{1}}.{{v}_{1}}+{{u}_{2}}.{{v}_{2}}+{{u}_{3}}.{{v}_{3}}\]

Exemplo 3: Dados os vetores \(u=\hat{i}-5\hat{j}+8\hat{k}\) e \(v=4\hat{i}-2\hat{j}-\hat{k}\), calcule o produto escalar de \(u\) por \(v\).

Solução: \(~u.v=1.\left( 4 \right)+\left( -5 \right).\left( -2 \right)+8.\left( -1 \right)=4+10-8=6\)

Observe que o resultado é um escalar e não um vetor.

As propriedades do produto escalar são as seguintes: dados quaisquer vetores \(u,~v\) e \(w\) e um escalar real \(\alpha \)

1. \(u.v=v.u\)
2. \(u.\left( v+w \right)=u.v+u.w~e~\left( u+v \right).w=u.w+v.w\)
3. \(\alpha \left( u.v \right)=\left( \alpha u \right).v=u.\left( \alpha v \right)\)

Definição Geométrica do Produto Escalar

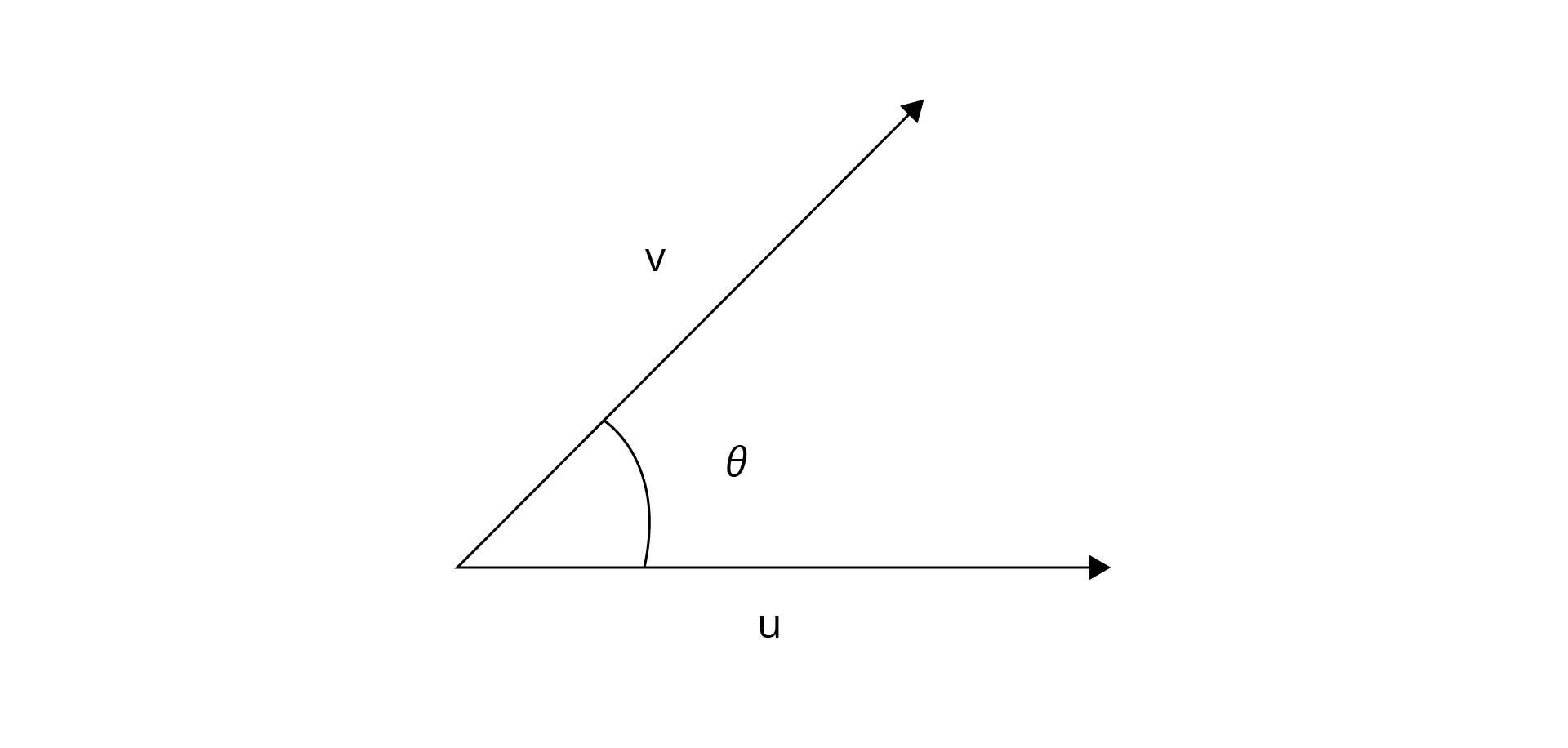
O produto escalar nos dá algumas relações entre os vetores, uma delas é o ângulo entre dois vetores. Como mostrado na figura 1.10 se u e v são vetores não nulos e 𝜽 o ângulo entre eles, então, o produto escalar de u por v nos diz que

\[u.v~=~\left| u \right|.\left| v \right|.cos\left( \theta  \right)~~~~~~(1)\]

onde \(0{}^\text{o}~\theta ~~~180{}^\text{o}\).

Através da definição dada pela equação (1) podemos calcular o ângulo θ entre dois vetores. Neste caso, isolamos o cosseno do ângulo na equação e obtemos:

\[cos\theta =\frac{u.v}{\left| u \right|\left| v \right|}~~~~~~(2)\]

Exemplo 4: Considerando os vetores \(u=\left( 1,1-1 \right)~\) e \(v=\left( 2,-1,0 \right)\), calcular o ângulo entre os dois vetores \(u\) e \(v\).

\[cos\theta =\frac{\left( 1,1,-1 \right).\left( 2,-1,0 \right)}{\sqrt{{{1}^{2}}+{{1}^{2}}+{{\left( -1 \right)}^{2}}}\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}}}\]

\[cos\theta =\frac{2-1}{\sqrt{3}\sqrt{5}}=0,26\]

\[\theta =arc\cos \left( 0,26 \right)={{75}^{0}}\]

Uma observação que podemos fazer será quando \(u.v~>~0\) o ângulo θ será agudo. Se \(u.v~<~0\), o ângulo θ será obtuso. Por fim, se \(u.v~=~0\), o ângulo será reto.

Ângulos Diretores

Outro conceito muito importante será o de ângulos diretores, por exemplo, como mostrado na figura 1.11.

Os ângulos diretores do vetor \(v\) dado pelas componentes \(\left( x,y,z \right)\) são os ângulos que o vetor forma com os eixos coordenados. Os cossenos diretores são os cossenos dos ângulos diretores que são calculados usando a definição da equação (2):

\[cos\alpha =\frac{\left( x,y,z \right).\left( 1,0,0 \right)}{\left| v \right|\left| {\hat{i}} \right|}=\frac{x}{\left| v \right|}\]

\[cos\beta =\frac{\left( x,y,z \right).\left( 0,1,0 \right)}{\left| v \right|\left| {\hat{j}} \right|}=\frac{y}{\left| v \right|}\]

\[cos\gamma =\frac{\left( x,y,z \right).\left( 0,0,1 \right)}{\left| v \right|\left| {\hat{k}} \right|}=\frac{z}{\left| v \right|}\]

Uma importante propriedade que encontramos com as definições dos cossenos diretores são:

\[co{{s}^{2}}\alpha +co{{s}^{2}}\beta +co{{s}^{2}}\gamma =1\]

Exemplo 5: Calcule os ângulos diretores do vetor \(v=\left( 1,-1,0 \right)\).

Primeiramente, vamos calcular o módulo do vetor \(v\):

\[v=\sqrt{{{1}^{2}}+{{\left( -1 \right)}^{2}}+{{0}^{2}}}=\sqrt{2}.\]

Usamos depois as definições dos cossenos diretores:

\[cos\alpha =\frac{x}{\left| v \right|}=\frac{1}{\sqrt{2}}\to \alpha ={{45}^{0}}\]

\[cos\beta =\frac{y}{\left| v \right|}=-\frac{1}{\sqrt{2}}\to \beta ={{135}^{0}}\]

\[cos\gamma =\frac{z}{\left| v \right|}=\frac{0}{\sqrt{2}}\to \gamma ={{0}^{0}}.\]

Vetores Ortogonais

Através da definição do produto escalar podemos verificar que dois vetores são ortogonais quando o produto escalar for nulo. Lembrando que dois vetores ortogonais têm um ângulo de 90º entre eles.

Exemplo 6: Considere dois vetores \(u=\left( a,-2 \right)\) e \(v=\left( 5,6 \right)\). Calcule o valor de a para que os dois vetores u e v sejam ortogonais.

\[\left( a,-2 \right).\left( 5,6 \right)=5a-12=0\to a=-12/5\]

Aplicações na parte computacional : O uso de vetores na parte computacional é de muita importância, pois na computação gráfica as posições de um objeto no espaço são representadas por vetores. Nessa parte, para que um objeto translade ou rotacione será aplicada uma matriz neste vetor posição. Entraremos em detalhes nessa parte nas unidades II e III.

Outro tipo de multiplicação de vetores chama-se produto vetorial. Nesse caso seria o produto de vetores em três dimensões R3. O módulo do resultado do produto vetorial pode ser escrito como:

\[\left| uxv \right|~=~\left| u \right|.\left| v \right|.sen\left( \theta  \right)~~~~~~(3)\]

Podemos ver na equação (3) que neste caso usamos a função trigonométrica \(sen\left( \theta  \right)\) o que implica que o módulo do produto vetorial será máximo quando o ângulo for 90º. Uma das aplicações do produto vetorial dentro da física será no contexto do cálculo do Momento da Força.

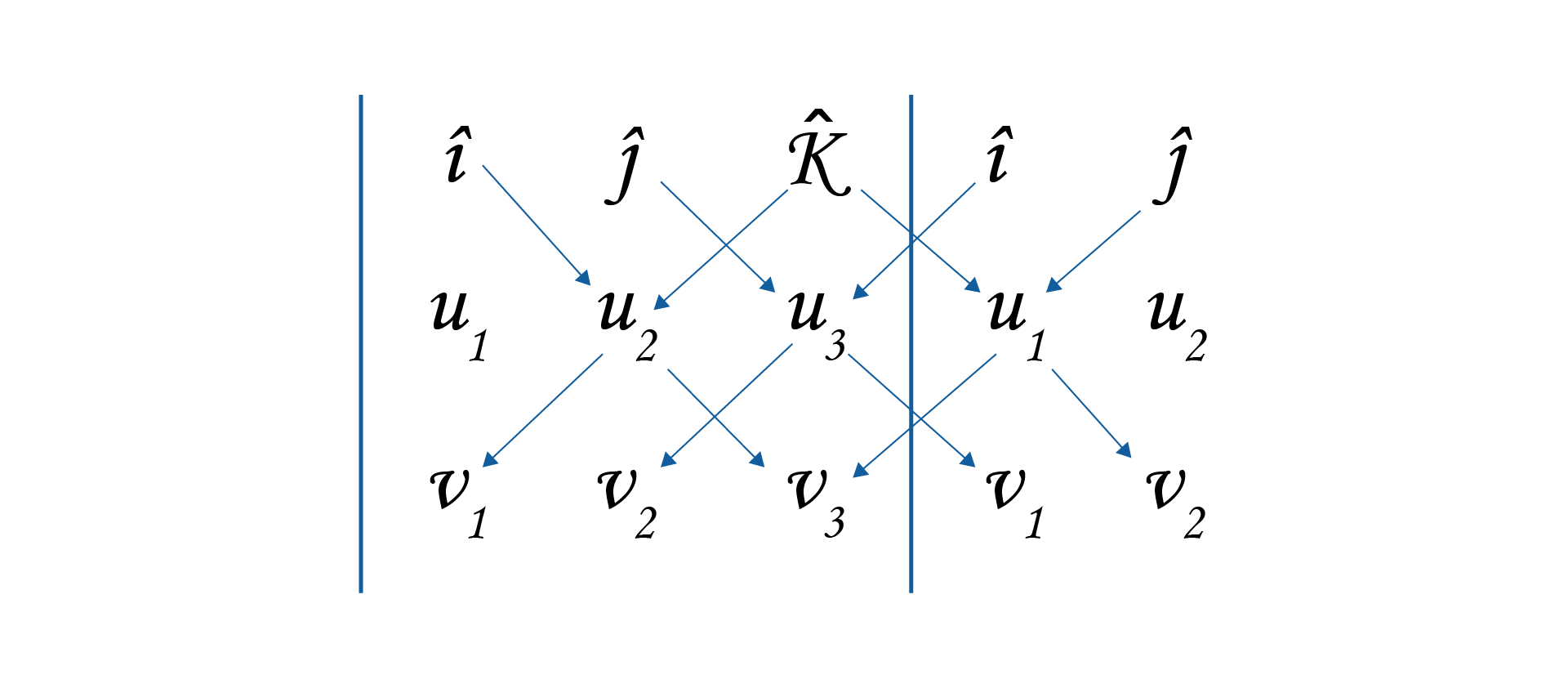
Além disso outro ponto a se destacar seria que o produto vetorial fornece como resultado outro vetor. Umas das maneiras para esse cálculo seria usar o determinante. Por exemplo, se temos dois vetores \(u=\left( {{u}_{1}},~{{u}_{2}},{{u}_{3}} \right)\) e \(v=\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right)\) o produto vetorial entre esses vetores será dado por:

\[\left| \begin{matrix}   {\hat{i}} & {\hat{j}} & {\hat{k}}  \\   {{u}_{1}} & {{u}_{2}} & {{u}_{3}}  \\   {{v}_{1}} & {{v}_{2}} & {{v}_{3}}  \\ \end{matrix} \right|~~~~~~(4)\]

Nessa situação o determinante dessa matriz será o resultado do produto vetorial. O cálculo desse determinante vai ser feito através da repetição das duas primeiras colunas e multiplicando cruzado. Esse esquema pode ser visto na figura 1.12. A multiplicação que vai da esquerda para direita consideramos positiva e da direita para esquerda negativa.

Mais precisamente se desenvolvermos esse cálculo encontraremos:

\[\hat{i}\left( {{u}_{2}}{{v}_{3}}-{{u}_{3}}{{v}_{2}} \right)+\hat{j}\left( {{u}_{3}}{{v}_{1}}-{{u}_{1}}{{v}_{3}} \right)+\hat{k}\left( {{u}_{1}}{{v}_{2}}-{{u}_{2}}{{v}_{1}} \right).~~~~(5)\]

Exemplo 7: Calcule o produto vetorial \(u~x~v\). Considere que \(u=\left( 1,2,3 \right)\) e \(v=\left( 0,1,-1 \right)\).

O resultado do produto vetorial será dado por:

\[u~x~v~=\hat{i}\left( 2.\left( -1 \right)-3.1 \right)+\hat{j}~\left( 1.\left( -1 \right)-3.0 \right)+\hat{k}\left( 1.1-2.0 \right)=-5\hat{i}+1\hat{j}+1\hat{k}.\]

O módulo desse vetor será dado por:

\[\left| u~x~v \right|=\sqrt{{{\left( -5 \right)}^{2}}+{{1}^{2}}+{{1}^{2}}=}\sqrt{27}.\]

Finalizando os conceitos de produto vetorial e escalar podemos deduzir algumas relações entre essas operações:

I.    \(~u.\left( u~x~v \right)=0\)

II.   \(v~\left( u~x~v \right)=0\)

III.  \(~u~x~\left( v~x~w \right)=\left( u.w \right)v~-~\left( u.v \right)w\)

Produto Misto

Consideremos três vetores u, v e w no espaço tridimensional. Desse modo, o produto misto desses três vetores será dado por:

\[u.\left( v~x~w \right)~~~~~~~~(6)\]

Na forma matricial teremos:

\[\left| \begin{matrix}   {{u}_{1}} & {{u}_{2}} & {{u}_{3}}  \\   {{v}_{1}} & {{v}_{2}} & {{v}_{3}}  \\   {{w}_{1}} & {{w}_{2}} & {{w}_{3}}  \\ \end{matrix} \right|\]

Assim para ter o resultado do produto misto devemos calcular o determinante.

Exemplo 8: Calcular o produto misto dos vetores \(u=~\left( 3,2,-1 \right),~v=\left( 0,2,-3 \right)~\) e \(w=\left( 2,6,-7 \right).~\)

Resolução: Colocando na forma matricial teremos:

\[\left| \begin{matrix}   3 & 2 & -1  \\   0 & 2 & -3  \\   2 & 6 & -7  \\ \end{matrix} \right|\]

O resultado do determinante desta matriz é 4.

\[u.\left( v~x~w \right)=4.\]

Nesta seção iremos apresentar as condições para a determinação de uma reta e um plano. Iremos identificar e escrever equações de retas nas formas vetorial, paramétrica e simétrica, escrever a equação geral do plano e verificar se um dado ponto pertence a uma reta ou plano.

Equação da Reta

As retas podem estar em planos (R²) ou no espaço (R³). Por exemplo, como mostrado na figura 1.13 a reta está no plano (x,y). No caso temos os pontos (0,3) e (2,5).

As retas no espaço possuem pontos com três coordenadas (x,y,z). Por exemplo na figura 1.14 temos que os pontos serão representados por três pontos.

Para determinar a equação da reta em um plano (x,y) usaremos a equação da reta:

\[y-{{y}_{0}}=m~\left( x-{{x}_{0}} \right)~~~~~~(8)\]

Onde m é o coeficiente angular da reta:

\[m=\frac{{{y}_{f}}-{{y}_{0}}}{{{x}_{f}}-{{x}_{0}}}.~~~~~~(9)\]

Para aplicar as equações acima vamos considerar o exemplo abaixo:

Exemplo 9: Escrever a equação da reta que passa pelos pontos \(\left( 0,0 \right)\) e \(\left( 2,3 \right)\).

Resolução: Primeiramente devemos calcular o coeficiente angular da reta:

\[m=\frac{3-0}{2-0}=\frac{3}{2}\]

A equação da reta vai ser dada por:

\[y-0=3/2\left( x-0 \right)\]

\[y=\frac{3}{2}x.\]

Equação Vetorial da Reta no Espaço

Uma reta pode ser determinada conhecendo-se dois de seus pontos ou conhecendo um de seus pontos e sua inclinação. Por exemplo, consideramos a seguinte equação vetorial:

\[AP=~tv\]

\[\left( x,y,z \right)=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)+t\left( a,b,c \right).~~~~~~~(10)\]

Exemplo 10: Determine a equação vetorial da reta r que passa pelo ponto A \(\left( 1,-1,4 \right)\) e tem a direção do vetor \(v=\left( 2,3,2 \right)\).

Resolução: Usando a equação 10 encontraremos

\[\left( x,y,z \right)=\left( 1,-1,4 \right)+t\left( 2,3,2 \right)~~~\]

Para obter as coordenadas de diversos pontos da reta temos que atribuir valores reais para o parâmetro t:

\[t=0~\to \left( x,y,z \right)=~\left( 1,-1,4 \right)\]

\[t=1\to \left( x,y,z \right)~=~\left( 3,2,6 \right)\]

\[t=2\to \left( x,y,z \right)~=~\left( 5,5,8 \right)\]

Equação paramétrica da reta no espaço

O conceito de equação paramétrica tem sua importância, quando precisamos determinar as coordenadas de um ponto na reta r, do qual sabemos uma de suas coordenadas. Para esse desenvolvimento considere a equação vetorial abaixo:

\[\left( x,y,z \right)=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)+t\left( a,b,c \right)\]

\[\left( x,y,z \right)=\left( {{x}_{0}}+at,{{y}_{0}}+bt,{{z}_{0}}+ct \right)\]

A partir das relações acima podemos obter as equações paramétricas:

\[x={{x}_{0}}+at\]

\[y={{y}_{0}}+bt\]

\[z={{z}_{0}}+ct.\]

Para aplicação do conjunto de equações acima faremos um exemplo:

Exemplo 11: Determine a equação paramétrica da reta que passa pelo ponto \(A\left( 3,-4,2 \right)\) e é paralela ao vetor \(v=\left( 2,1,-3 \right)\).

Resolução: Neste caso usamos o conjunto de equações paramétricas e encontramos:

\[x=3+2t~\]

\[y=-4+1t\]

\[z=2-3t.\]

Vamos supor dois pontos B e C da reta r, com os parâmetros \(t=2\) e \(t=3\) obtemos:

\[x=3+2.2=7,~~x=3+2.3=9\]

\[y=-4+1.2=-2,~~y=-4+1.3=-1\]

\[z=2-3.2=-4,~~~~~~~~~~~~z=2-3.3=-7.\]

Encontramos os seguintes pontos:  \(B=\left( 7,-2,-4 \right)\) e \(C=\left( 9,-1,-7 \right)\).

Equações Simétricas da Reta

Para obter as equações simétricas da reta podemos isolar o parâmetro t das equações paramétricas. Por exemplo, considere o conjunto de equações:

\[x=3+2t~\]

\[y=-4+1t\]

\[z=2-3t.\]

Se isolarmos o parâmetro t das equações e igualarmos cada um encontramos:

\[\left( x-3 \right)/2=y+4=\left( 2-z \right)/3.\]

Equações do Plano

Para determinação da equação geral do plano consideramos a figura 1.16. Seja um ponto A (x0,y0,z0) que pertence a um plano 𝝰 e n = (a,b,c) um vetor normal ao plano. O plano 𝝰 pode ser definido como um conjunto de todos os pontos P(x,y,z) do espaço tais que o vetor AP é ortogonal a n . O ponto P pertence a um determinado plano se, e somente se:

\[n.AP=0\]

Lembrando que a operação acima é o produto escalar entre dois vetores. Se levarmos em conta isso encontramos a equação geral do plano:

\[ax+by+cz+d=0\]

Onde \(d=-\left( a{{x}_{0}}+b{{y}_{0}}+c{{z}_{0}} \right)\).

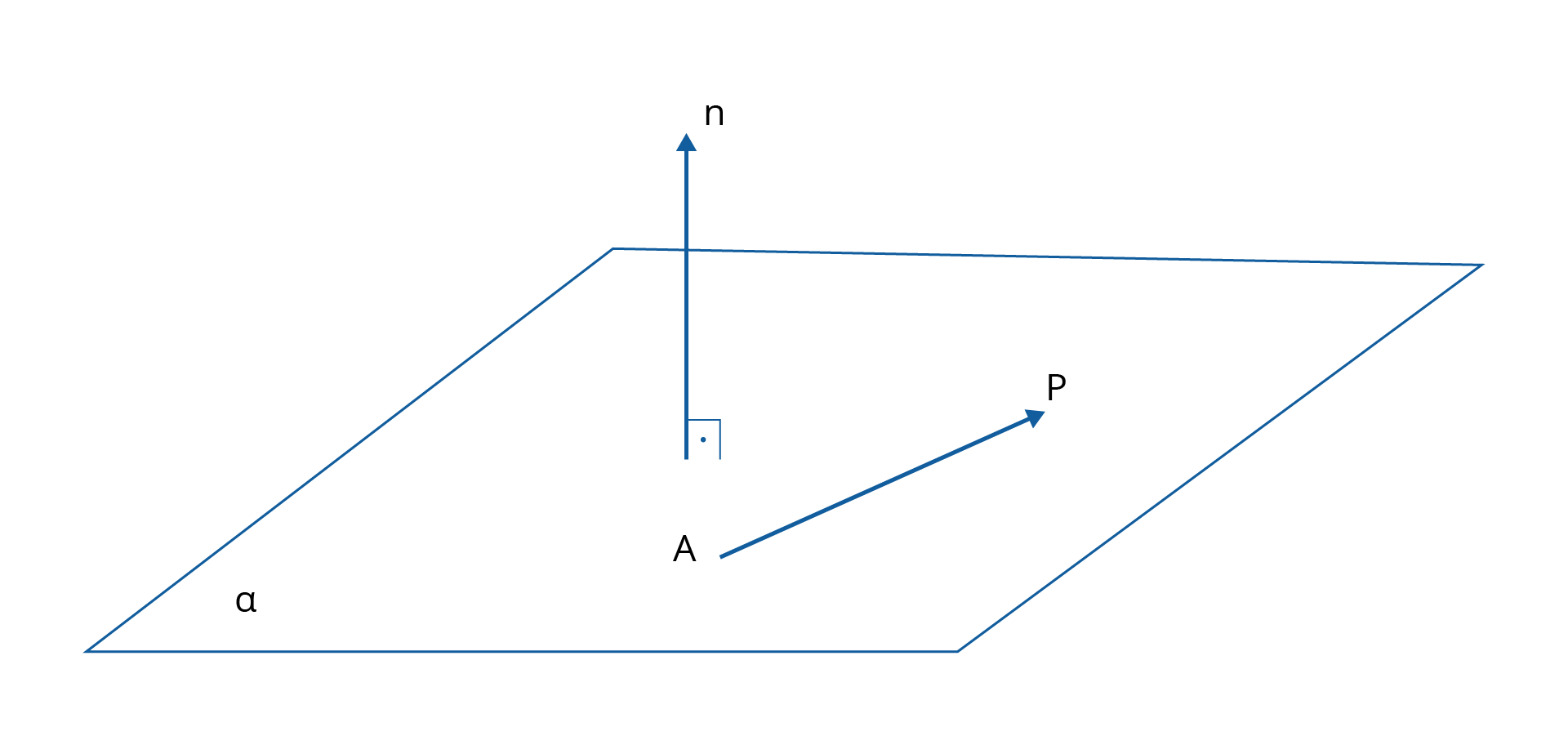
Outro conceito importante será que o vetor \(n\) ortogonal ao plano será ortogonal a qualquer outro vetor representado nesse plano.

Exemplo 12: Determine a equação paramétrica da reta que passa pelo ponto \(A\left( 3,-4,2 \right)\) sabendo que o vetor \(v=\left( 2,1,-3 \right)\) é normal ao plano.

Resolução: \(AP.v=0~\to ~\left( x-3,~y+4,~z-2 \right).\left( 2,1,-3 \right)=0~\to 2x-6+y+4-3z+6=0\to 2x+y-3z+4=0\).

Posições Relativas entre Retas e Planos

Dado um plano 𝞹 de equação geral:

\[ax+by+cz=d\]

e uma equação paramétrica da reta r:

\[\left( x,y,z \right)=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)+t\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right).\]

Nessa situação a reta e o plano serão transversais se:

\[\left( a,b,c \right).\left( {{v}_{1}},{{v}_{2}},{{v}_{3}} \right)\ne 0.\]

Se a reta r não for transversal ao plano 𝞹, teremos:

A reta r é paralela ao plano 𝞹 de forma disjunta do plano.

Ou a reta r está contida no plano 𝞹.

Exemplo 13: Mostre que a reta abaixo é paralela ao plano.

Equação da reta \(\left( x,y,z \right)=\left( -2,1,-5 \right)+t\left( 3,-4,4 \right)\)

Equação do plano \(4x-3y-6z-5=0\)

Resolução:

Vetor diretor da reta: \(v=\left( 3,-4,4 \right)\)

Vetor normal ao plano: \(n=\left( 4,-3,-6 \right)\)

Usando o produto escalar entre estes dois vetores teremos:

\[\left( 3,-4,4 \right).\left( 4,-3,-6 \right)=12+12-24=0\]

Desse modo, a reta é paralela ao plano.

Posições Relativas entre Planos

Dois planos podem ser paralelos, transversais e coincidentes. Por exemplo, sejam dois planos:

\[{{\pi }_{1}}:~{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z={{d}_{1}}\]

\[{{\pi }_{2}}:~{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z={{d}_{2}}\]

\({{\pi }_{1}}\) e \({{\pi }_{2}}\) são planos paralelos se os seus vetores normais forem paralelos.  Contudo, se:

\[\left( {{a}_{1}},{{b}_{1}},{{c}_{1}},{{d}_{1}} \right)=\lambda \left( {{a}_{2}},{{b}_{2}},{{c}_{2}},{{d}_{2}} \right)\]

onde \(\lambda \) é uma constante de proporcionalidade, temos que os planos são coincidentes.  Se não existe a proporcionalidade acima os planos são paralelos distintos.

No caso se \({{\pi }_{1}}\) e \({{\pi }_{2}}\) forem transversais temos que vetores normais não são paralelos. Ou seja, não existe a proporcionalidade entre \(\left( {{a}_{1}},{{b}_{1}},{{c}_{1}},{{d}_{1}} \right)~\) e \(\left( {{a}_{2}},{{b}_{2}},{{c}_{2}},{{d}_{2}} \right)\). Se os planos forem transversais, então a reta r determinada pela interseção dos dois planos deve ser perpendicular aos vetores normais \(\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)~\) e \(\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)\).