Cálculo Aplicado - Uma Variável
Trigonometria e Noções de Limites
Nesta unidade, estudaremos importantes conceitos da trigonometria com ênfase nas propriedades do triângulo retângulo, ciclo trigonométrico e funções trigonométricas. A trigonometria é a área da Matemática que trata dos problemas envolvendo ângulos e medidas, que podem ser aplicados na resolução de problemas relacionados a várias áreas de conhecimento. A construção de gráficos definidos por várias sentenças proporciona o entendimento das noções intuitivas de limites e continuidade de uma função em um dado ponto. Esses conceitos são importantes para entendermos os operadores derivada e integral de funções, que estudaremos em outras disciplinas. Portanto, convido-lhe a obter novos conhecimentos matemáticos, para que seja capaz de solucionar problemas diversos do dia a dia.
Desde os tempos remotos, a humanidade observava a posição dos astros celestiais, e a relação entre eles foi de suma importância para o estudo de desenvolvimento da astronomia. Nesse sentido, outros estudos foram necessários para o desenvolvimento do setor da agricultura (agrimensura) e transporte, com as navegações. Para tanto, foi de suma importância o estudo da trigonometria, cujo termo vem do grego trigonon , que significa triângulo, e metron , que significa medida. Segundo Costa (1997), há registros de que Hiparco de Nicéia (180-125 a.C.), astrônomo grego que viveu no século 2 a.C., é considerado o “pai da trigonometria”. Existem infinitas aplicações da trigonometria, desde determinação de distâncias, resolução de funções e problemas matemáticos, até o cálculo de velocidades, acelerações, entre outras grandezas vetoriais.
Segundo Demana et al . (2013), os triângulos são classificados em relação aos seus lados como: equiláteros (comprimentos dos três lados iguais), isósceles (comprimento de dois lados iguais) e escalenos (comprimento dos três lados diferentes). Observe, na Figura 1.1, o triângulo equilátero com os três lados iguais, cujos ângulos também são iguais a 60°, o triângulo isósceles com dois lados iguais e, por fim, o triângulo escaleno com os três lados diferentes. Quanto aos ângulos, os triângulos podem ser classificados como acutângulo (três ângulos internos menores que 90° – ângulos agudos), obtusângulo (um ângulo interno maior do que 90° – ângulo obtuso) ou retângulo (um ângulo interno igual a 90°). A Figura 1.1 mostra os três tipos de triângulos, evidenciando seus lados e ângulos.
Vale ressaltar que a soma dos ângulos internos de um triângulo qualquer é igual a 180°. Daremos ênfase ao estudo do triângulo retângulo que possui um ângulo reto (90°) entre dois de seus lados. Verifique que qualquer um dos triângulos – equilátero, isósceles ou escaleno – pode ser dividido em triângulos retângulos. Dessa forma podemos simplificar a resolução de uma infinidade de problemas.
Por sua vez, a Figura 1.2 mostra um triângulo retângulo em que os pontos A, B, e C representam os vértices, o lado maior é chamado de hipotenusa, e os demais de cateto oposto (CO\ (ângulo)) e o cateto adjacente (CA\ (ângulo)).
Pitágoras viveu entre 570 a.C. e 495 a.C., na Grécia Antiga. Ele foi um filósofo e matemático grego que influenciou as ciências contemporâneas. Para ele, o que interessava eram os números, sua relação com formas geométricas e padrões celestes. Além disso, ele acreditava que o próprio cosmos teria uma relação mais íntima com números. Para conhecer um pouco mais a respeito desse personagem histórico, acesse o link abaixo e leio texto “Pitágoras”, de Alexsandra Oliveira Andrade.
Fonte: Andrade (2019, on-line ).
O teorema proposto por Pitágoras (570 - 495 a.C.) relaciona a medida dos diferentes lados de um triângulo retângulo. Esse teorema afirma que:
A soma dos quadrados dos comprimentos dos catetos é igual ao quadrado do comprimento da hipotenusa.
Considere o triângulo da Figura 1.3, em que temos o cateto oposto e o cateto adjacente ao ângulo alfa. Portanto, pelo teorema de Pitágoras:
\(H^{2}{=\left[CA(\alpha)\right]^2+}{{\left[CO(\alpha)\right]^2}}\).
De forma geométrica, é possível provar o teorema de Pitágoras, como mostra a Figura 1.4. A medida do lado AC ao quadrado representa a área do quadrado definido pelo lado AC. Seguindo o mesmo raciocínio, para os outros lados verifica-se que a área do quadrado definido por AC é igual à soma das áreas dos quadrados definidos por AC e BC.
Na prática, o teorema de Pitágoras é utilizado para resolver problemas simples encontrados no nosso dia a dia. Por exemplo, um pedreiro utiliza o teorema de Pitágoras para fazer marcação de paredes que fazem um ângulo reto (90°) entre elas. Na linguagem dos pedreiros, isso é chamado de “deixar no esquadro”.
Verifique a marcação dos pilares numa construção, na Figura 1.5.
Para a = 30 cm, b = 40 cm, c = 50 cm, temos, por Pitágoras, que: 30² + 40²= 50².
Outras relações do triângulo retângulo, que envolve medidas dos seus lados e ângulos internos possibilita a resolução de uma infinidade de problemas aplicados em várias áreas de conhecimento.
Considere a Figura 1.6 e verifique as relações no Quadro 1.1, definindo o seno, cosseno, tangente, cotangente, secante e cossecante do ângulo alfa.
Além das relações trigonométricas apresentadas, há a equação fundamental trigonométrica em que \(sen^2x+cos^2x=1\). Outras equações trigonométricas muito utilizadas na resolução de problemas são apresentadas no Quadro 1.2:
É possível determinar facilmente as relações trigonométricas do triângulo retângulo para os ângulos do primeiro quadrante, 30°, 45° e 60°. Com ajuda dos triângulos apresentados a seguir, verifique os dados obtidos na tabela com indicações dos valores de seno, cosseno e tangente dos ângulos desses ângulos notáveis.
A seguir, apresentamos a tabela com as razões trigonométricas:
Utilizando os triângulos, verifique os dados obtidos na tabela com indicações dos valores de seno, cosseno e tangente dos ângulos desses ângulos notáveis.
O observador da figura a seguir tem 1,50 m de altura e vê o topo da torre segundo um ângulo de 60° com a horizontal. Ao se afastar da torre a distância de 6.√3 m, a contar de onde ele estava e ao longo da semirreta horizontal definida na figura, ele passa a ver o mesmo ponto por um ângulo de 30°, agora com a vertical.
SANTOS, A. J. de A. 1000 Testes de Matemática . 5. ed. Salvador: Colégio Anchieta, 2005. v. 3.
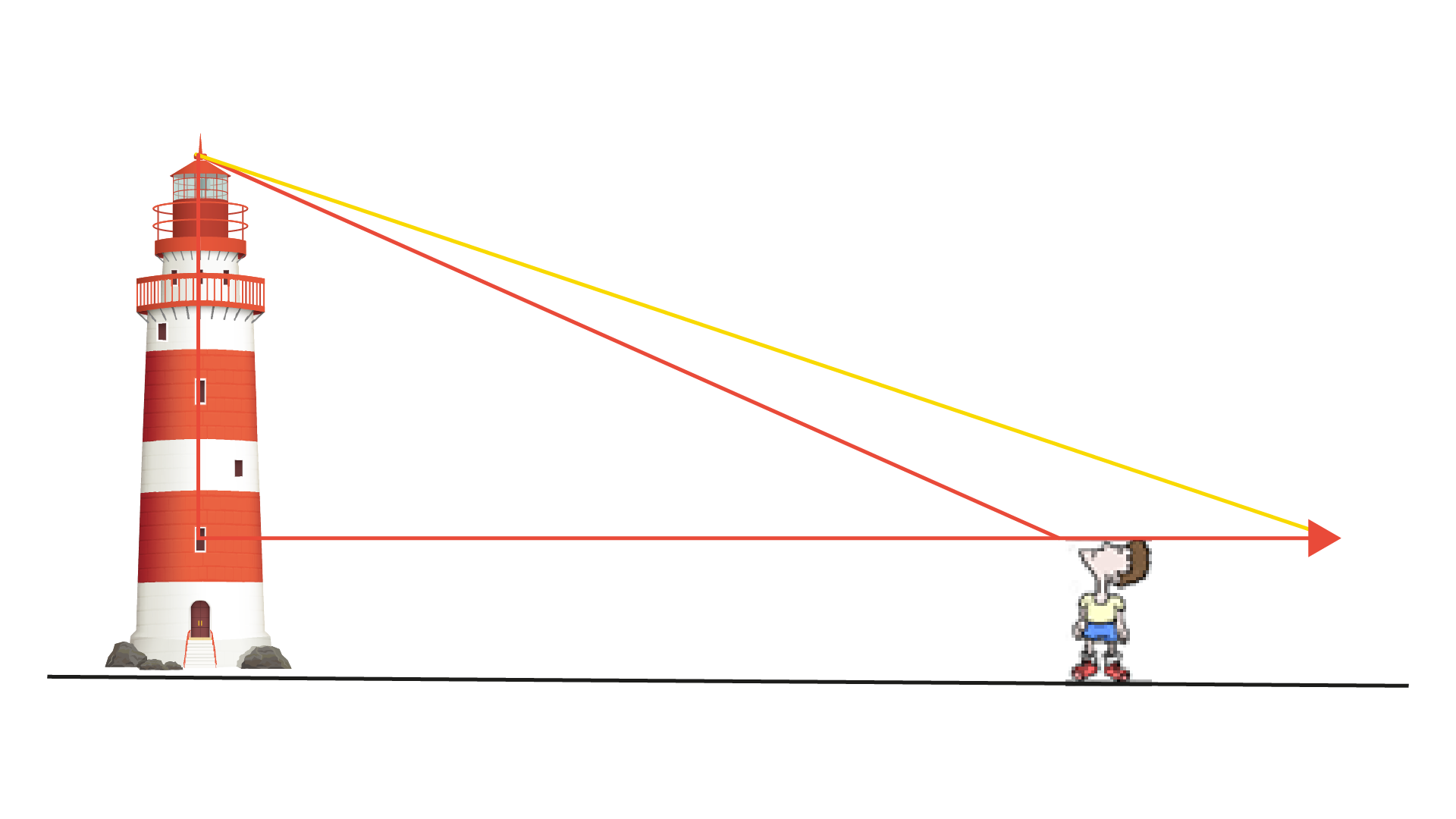
Observando as informações e a Figura 1.8, assinale a alternativa correta, que corresponde à altura da torre.
Na figura a seguir, a reta representa a trajetória de um avião que voa a 600 km/h. Um observador, parado no ponto P da superfície da Terra, num dado instante, vê o avião no ponto \(T_1\), segundo um ângulo de alfa igual a 30 graus. Um minuto depois, esse observador vê o mesmo avião, no ponto \(T_2\) , segundo outro ângulo, theta igual a 45 graus. Considere:
SANTOS, A. J. de A. 1000 Testes de Matemática . 5. ed. Salvador: Colégio Anchieta, 2005. v. 3.
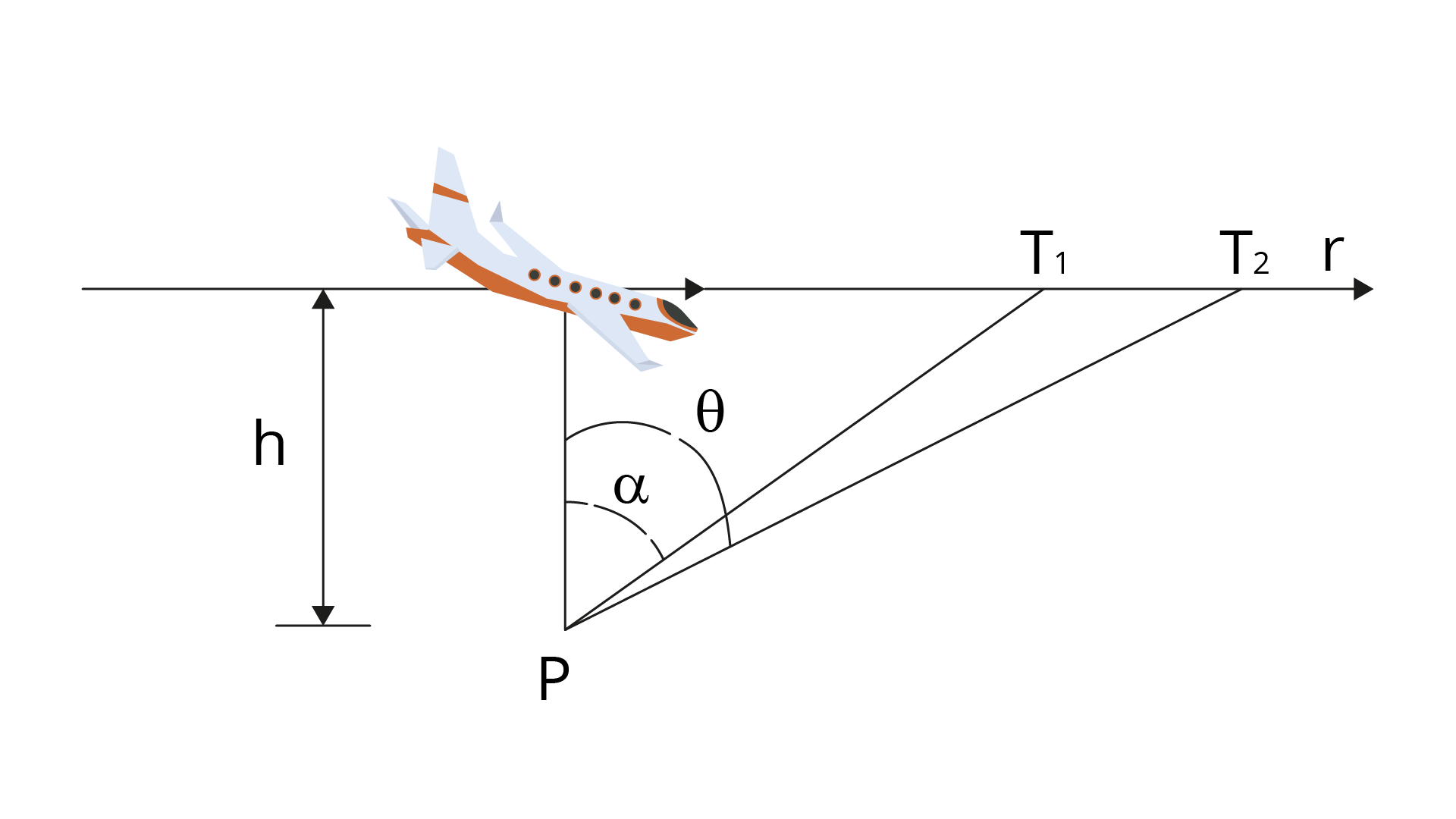
Assinale a alternativa que corresponde corretamente à altura da trajetória do avião em relação a Terra.
Nesta seção, você vai conhecer uma importante ferramenta, que o auxiliará para determinação das razões trigonométricas: o ciclo trigonométrico . Para aprender trigonometria, é necessário ter domínio do ciclo trigonométrico, em que será possível estabelecer relações entre arcos (ângulos), distâncias (radianos) e respectivas funções trigonométricas seno, cosseno e tangente que pode facilitar a resolver diversos problemas e situações que envolvam a trigonometria. Acompanhe o passo a passo.
O ciclo trigonométrico consiste no traçado de um ciclo de raio 1 centrado na origem do plano cartesiano. O eixo horizontal das abscissas fornece a medida do cosseno de um ângulo, formado a partir do ponto (1, 0) no sentido anti-horário. Já o eixo vertical das ordenadas, fornece a medida do seno do mesmo ângulo indicado (DEMANA et al., 2013).
A Figura 1.8 mostra um ciclo trigonométrico em que é possível verificar a leitura do cosseno de um ângulo através da projeção ortogonal do ângulo no eixo das abcissas, e do seno de um ângulo por meio da projeção ortogonal no eixo das ordenadas.
Observe que, no ciclo há a representação dos ângulos, variando de 0 até 360° ou em radianos que varia de 0 até 2π.
O radiano (1 rad) é definido como a medida do ângulo central, cujo arco correspondente representa o mesmo comprimento (C) do raio (R) da circunferência (Figura 1.8).
Com a observação do ciclo trigonométrico é possível determinarmos o sinal do cosseno, seno e tangente de ângulos localizados nos 4 quadrantes. Confira você mesmo, analisando a Figura 1.9. Verifique que a leitura da tangente é realizada ao prolongar o ângulo até a reta vertical.
Para converter radianos para ângulos em graus podemos usar uma regra de três simples, uma vez que 1 radiano equivale aproximadamente 57,30 graus, como a Figura 1.8 mostrou anteriormente. Por exemplo: para saber quantos radianos equivale o ângulo de 30 graus, efetuar a regra de três:
\[180° \rightarrow\ \pi\]
\[\ \ 30° \rightarrow\ x\ \ \ x=\frac{30\ \pi}{180}=\frac{\pi}{6}rad\]
Por meio do ciclo trigonométrico é possível determinar as razões trigonométricas para os ângulos principais, conforme a Tabela 1.2:
Observe que, não é possível determinar as tangentes para os ângulos de 90° e 270°. Nesse caso, a reta determinada por esses ângulos fica paralela a reta para leitura da tangente e, portanto, ao efetuar o prolongamento as retas não se encontram.
Consequentemente, para alguns ângulos também não é possível determinar a cotangente, secante e cossecante.
Com base no ciclo trigonométrico da Figura 1.4, observe os sinais das razões trigonométricas em alguns ângulos, conforme apresentados na Tabela 1.3. Basta localizar os ângulos nos quadrantes do ciclo trigonométricos e verificar o sinal correto na marcação em vermelho na tabela.
Para a determinação dos valores das funções trigonométricas de um determinado ângulo, que se encontra no 2º, 3º e 4º quadrantes, basta seguirmos os seguintes passos:
Vamos fazer a redução do 1º quadrante do ângulo, equivalente a 120°, que se encontra no 2º quadrante. Avaliando o sinal do seno e do cosseno neste quadrante, percebemos que o seno é positivo, enquanto, o cosseno é negativo, observe a Figura 1.10:
Como \(\pi<\frac{2\pi}{3}<\frac{\pi}{2}\) tomamos o intervalo superior para aplicar a redução, logo, \(\pi-\frac{2\pi}{3}=\frac{\pi}{3}\). Portanto:
A relação fundamental da trigonometria \(sen^2x+cos^2x=1\) resulta do teorema de Pitágoras (Figura 1.11):
Dividindo a expressão por \(sen^2x\), obtemos: \(1 + cotg^2x = cossec^2x\). Dividindo a expressão por \(cos^2x\), obtemos: \(tg^2x + 1 = sec^2x\).
Analisando os triângulos retângulos apresentados a seguir, verificamos os resultados de cada valor trigonométrico que foi apresentado na Figura 1.11.
Até aqui, ao estudarmos a trigonometria, envolvemos algumas funções trigonométricas e suas características. Neste tópico, abordaremos com detalhamento o estudo de tais funções, inclusive utilizando a análise gráfica.
A seguir verifique a construção gráfica de várias funções trigonométricas, assim como algumas informações importantes.
valores que a abscissa x pode assumir tal que a imagem y seja um valor real.
valores, que a ordenada y assume.
par e ímpar
comprimento do intervalo no qual a função passa por um ciclo completo de variação.
o sinal que a função assume para ângulos localizados em cada quadrante.
Intervalos em que a função é crescente e/decrescente.
Nesta seção, estudaremos as funções trigonométricas inversas: arco seno, arco cosseno, arco tangente, arco cotangente, arco secante e arco cossecante. Segundo Demana et al. (2013), essas funções trigonométricas não são injetoras, portanto, não admitem a existência de função inversa. Entretanto, é possível restringir o seu domínio de forma que sejam inversíveis. A seguir, apresentaremos cada uma dessas funções com seus domínios e imagem adequados convenientemente, de forma a garantir a existência da função inversa.
Como exemplo, em relação à função arco seno, pergunta-se: qual é o arco (ângulo) cujo seno é igual a 1? (Resposta: 90 graus).
Portanto, para as funções inversas seu domínio passa a ser a imagem da função a ser invertida e sua imagem é o domínio da função original.
Portanto, para as funções inversas seu domínio passa a ser a imagem da função a ser invertida e sua imagem é o domínio da função original.
A figura a seguir apresenta um gancho fixado na parede em que duas forças estão atuando através de dois cabos. Determine as projeções das forças representadas pelos dois vetores nas direções horizontais e verticais. Os valores das forças e ângulos estão sinalizados na figura.
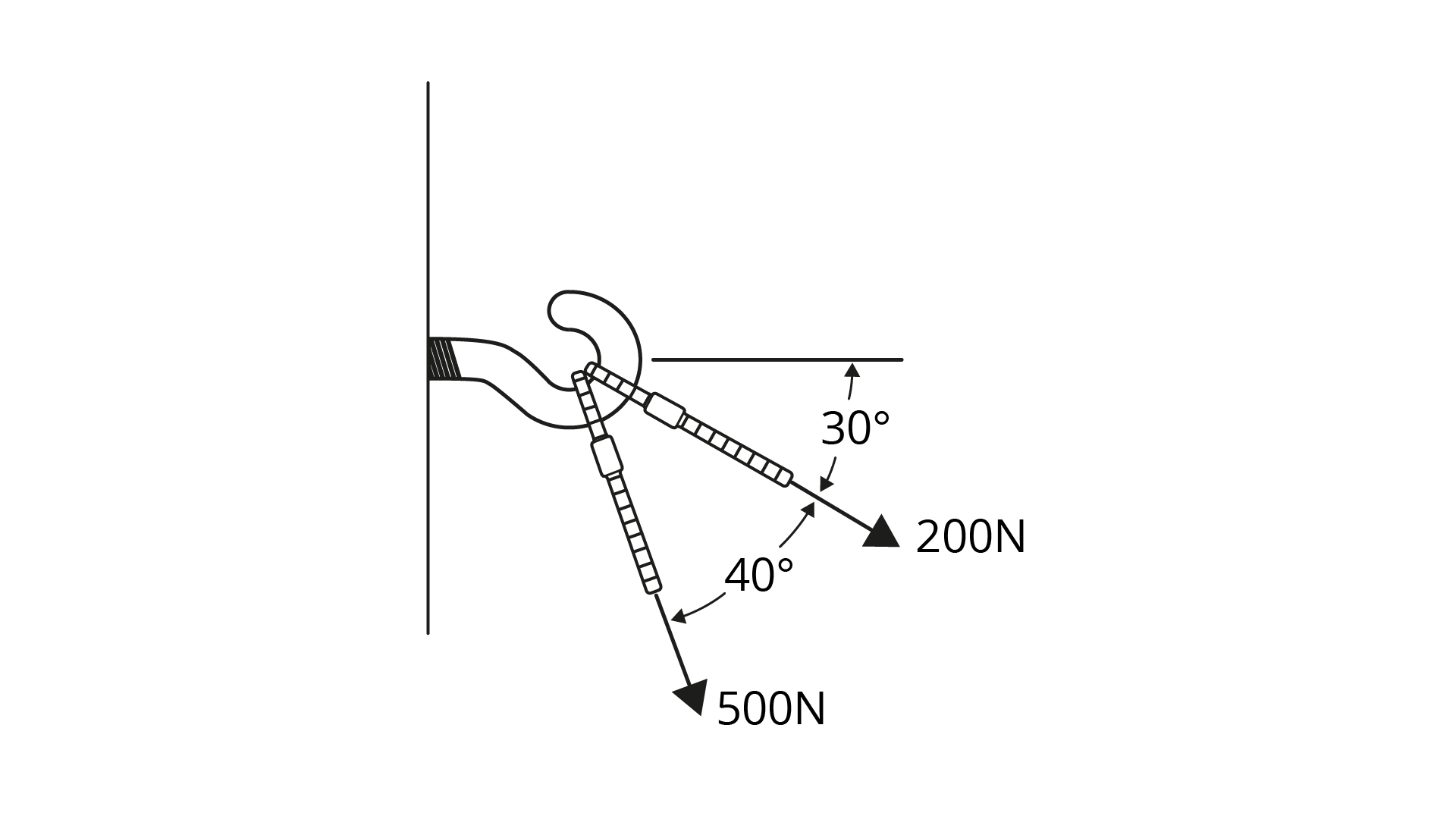
Em relação aos resultados obtidos, assinale a alternativa correta.
No ciclo trigonométrico da figura a seguir, identifique o ângulo correspondente, situado no primeiro quadrante. Após a redução ao primeiro quadrante, determine o seno desse ângulo.
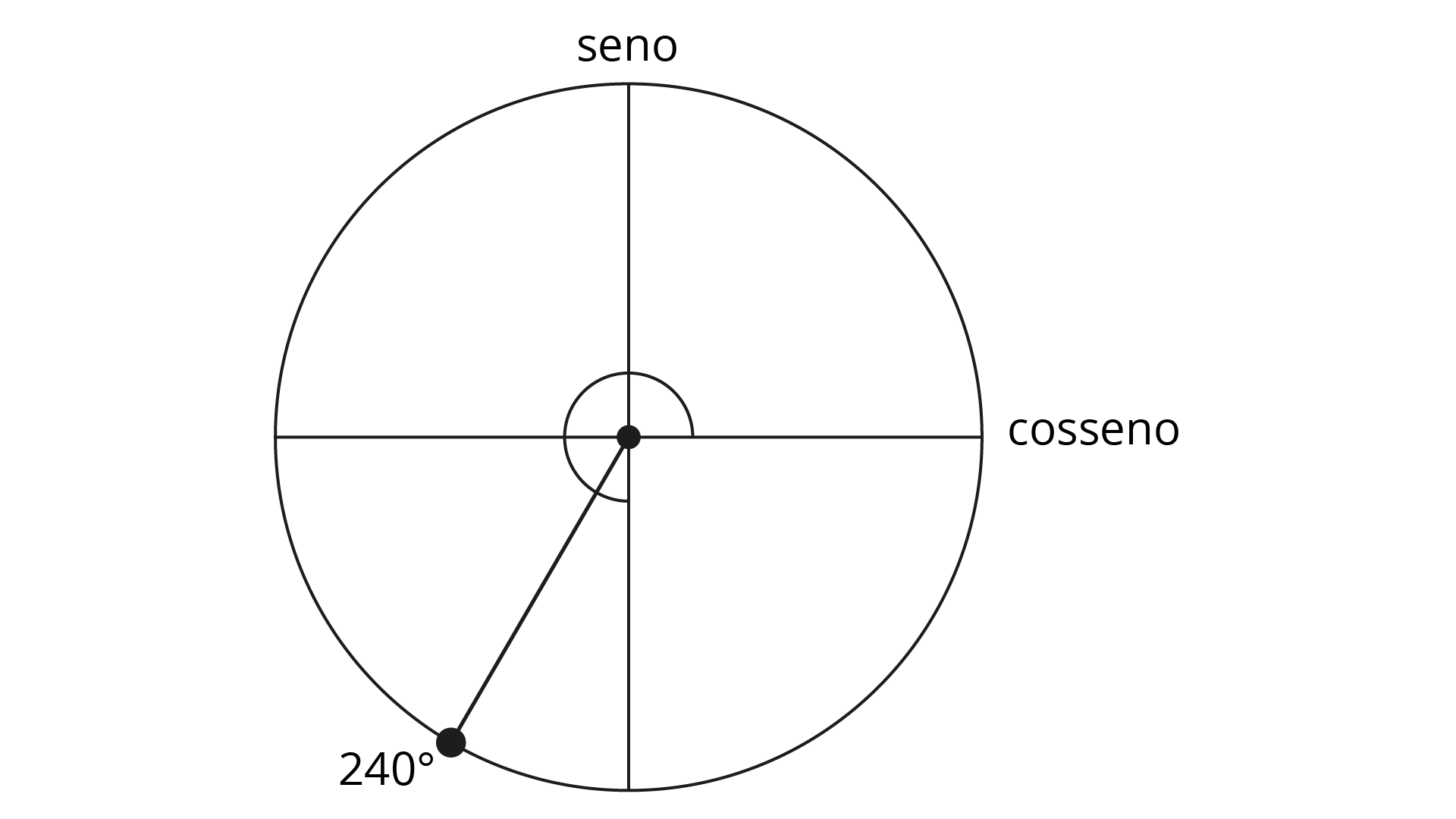
Assinale a alternativa correspondente ao seno desse ângulo.
Nesta seção, mostraremos como construir gráficos definidos por várias sentenças. Dessa forma, obtemos excelente ferramenta para trabalharmos o conceito de limites através de uma noção intuitiva. A partir disso, teremos condições de estudar a continuidade de uma função.
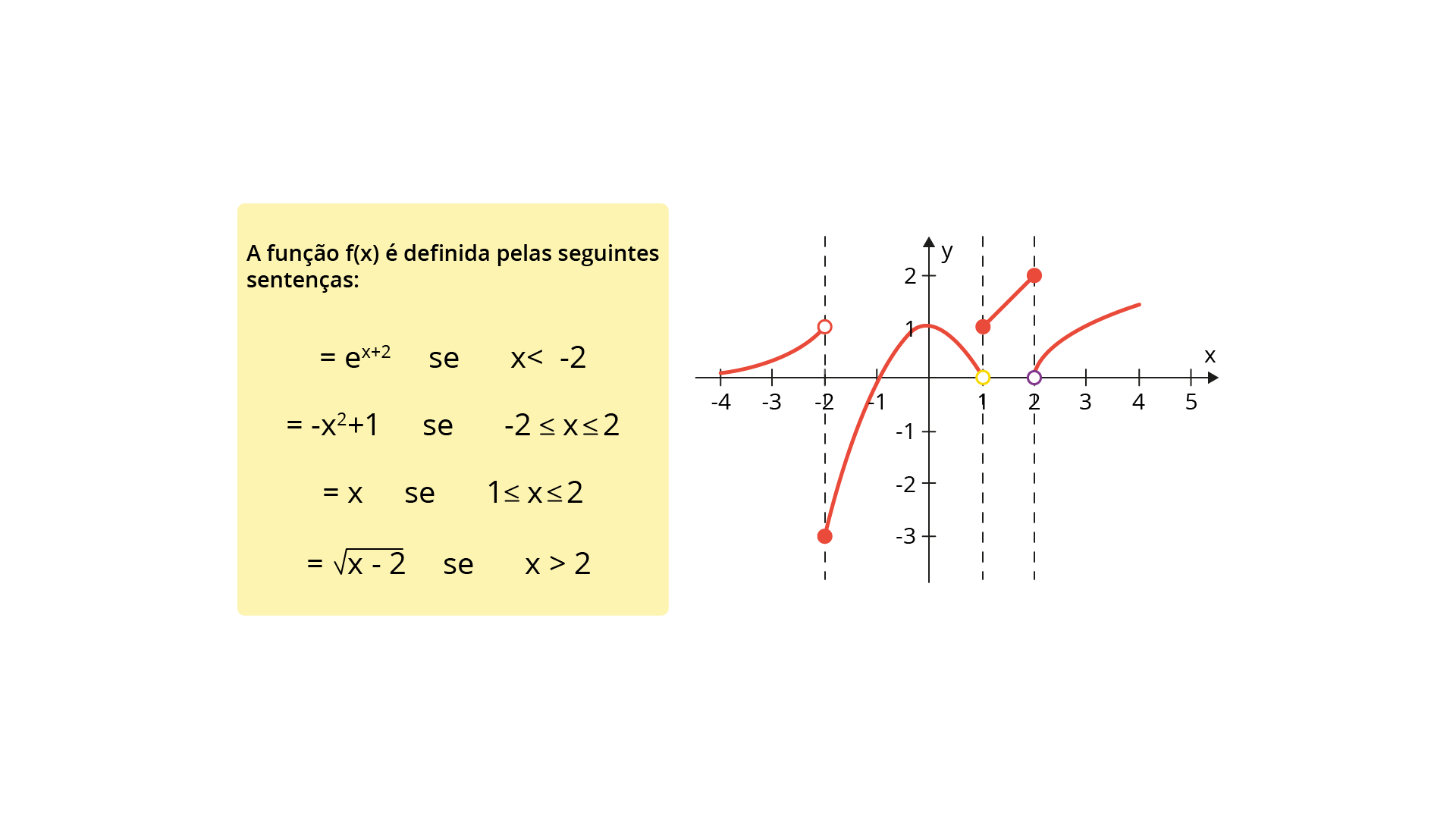
Uma função f(x) é definida em várias sentenças, como o exemplo a seguir:
Verifique que o gráfico da Figura 1.12 é representado por partes de vários gráficos de funções elementares. Nesse sentido, é importante a marcação dos pontos ao final dos intervalos, que quando fechado é representado por o ciclo cheio e, quando o intervalo é aberto, o ciclo fica vazado. Nesse exemplo, em especial, temos uma função exponencial na primeira sentença, depois uma parábola com concavidade para baixo, uma reta representada pela primeira bissetriz e, por fim, a função de uma raiz quadrada.
Para realizar a construção gráfica, é necessário que você revise a construção gráfica de cada um dos gráficos elementares e sua movimentação gráfica. Para determinar o domínio de tais funções, ou mesmo se um dado gráfico representa uma função, é necessário observar relações entre as variáveis x e y.
Verifique, nos exemplos a seguir, alguns comentários para elucidar o conceito de domínio e imagem de funções definidas por várias sentenças.
Analise a figura a seguir:
Dada a função racional \(f(x)=\frac{x^2-4}{x-2}=\frac{(x+2)(x-2)}{x-2}=x+2\), verifica-se que o gráfico da Figura 1.14 dessa função é uma reta, porém o domínio da função é \(\mathfrak{R}-\left\{2\right\}\).
Após analisar o gráfico, o que acontece com o valor da função f(x) quando x se aproxima de 2? Reflita.
O gráfico ao se aproximar de 2 pela esquerda: \(x\rightarrow2^-\) “lemos: x tende a 2 pela esquerda”, e ao se aproximar de 2 pela direita: \(x\rightarrow2^+\) “lemos: x tende a 2 pela direita”, em ambos os casos, verifica-se que o valor da função se aproxima de 4. Portanto, definimos que os “limites laterais” da função quando x tende a 2 pela esquerda e pela direita são iguais a 4, portanto, podemos afirmar que o limite da f(x) quando x tende a 2 existe e é igual a 4.
Em notação matemática, temos:
\(\lim_{x\rightarrow 2}-f(x)=\lim_{x \rightarrow 2^+}f(x)=4\rightarrow \lim_{x \rightarrow 2}f(x)=4\)
Definição: considere uma função \(f:D\subset\mathfrak{R}\rightarrow\mathfrak{R}\) definida em um intervalo aberto \(D\) e \(x_o\) pertencente a \(D\). Consideramos que ela é contínua em \(x_o\) se satisfaz as seguintes condições:
(i) \(\lim_{x\rightarrow x_0}f(x)=L\) existe. Ou seja, \(\lim_{x\rightarrow x_{0^+}} f(x)= \lim_{x \rightarrow x_{0^-}}f(x)=L\)
(ii) \(\lim_{x\rightarrow x_{0}} f(x)= f(x_0)\)
Agora, leia as duas observações a seguir e analise cada gráfico apresentado na Figura 1.15 sobre a existência de limites num dado ponto.
(1) Para que o limite de uma função exista num ponto, basta que os limites laterais existam (quando for possível determiná-los) e sejam iguais. Não é necessário que a função seja definida nesse ponto.
(2) Uma função pode ter limite num ponto e não ser contínua. Isso acontece quando os limites laterais são iguais, mas o valor da função no ponto é diferente do valor do limite.
Por meio da análise dos gráficos da Figura 1.16 você pode verificar que o limite pode existir e o seu valor ser diferente do valor da função no ponto. Nesse caso, dizemos que a função não é contínua nesse ponto.
Fisicamente podemos mostrar que as descontinuidades estão associadas a muitos processos e fenômenos que ocorrem na prática. Elas indicam a ocorrência de importantes fenômenos físicos. Nesse sentido, observe a figura a seguir.
Observe que, houve queda de voltagem para zero de maneira repentina. Nesse caso, por exemplo, podemos ter uma conexão mal feita, induzindo a uma descontinuidade na transmissão de um sinal elétrico.
É de suma importância dominar a existência de limites, através da análise dos limites laterais, relativo à um ponto, é possível determinar se uma função é contínua nesse ponto. Nesse contexto, considere uma função f: D → IR e \(x_o\) um ponto interior desse intervalo e avalie as afirmativas a seguir, sinalizando (V) para as afirmativas verdadeiras ou (F) para as afirmativas falsas.
I. ( ) Para uma função ter limite num ponto \(x_o\) é importante que ela esteja definida nesse ponto.
II. ( ) Uma função pode ter limite num ponto \(x_o\) e não ser contínua nesse ponto.
III. ( ) Para uma função ser contínua em \(x_o\) é necessário que os limites laterais sejam iguais.
IV. ( ) Quando os limites laterais são iguais no ponto \(x_o\), a função é contínua nesse ponto.
V. ( ) Pode existir uma função contínua em \(x_o\) que não tenha limites laterais iguais.
Assinale a alternativa que apresenta a sequência correta:
4) As coordenadas polares facilitam o cálculo de integrais duplas quando é complicado escrever a região na qual a função está definida em coordenadas retangulares. Utilizando as coordenadas polares, encontramos que o volume do sólido limitado pelo plano \(z=0\) e pelo paraboloide \(z = 1 - x^2 - y^2\) é igual a:
Por meio da análise gráfica, complete a tabela a seguir em relação ao limite nos pontos solicitados:

Editora: Zahar
Ano: 1972
Autor: Peter Bentley
ISBN: 978-85-378-0134-5
Comentário: esse livro reporta um resumo de muitas descobertas matemáticas aplicadas a várias áreas de conhecimento através de uma história ilustrada. Você entenderá como surgiram os números "e" (base do logaritmo neperiano), "\(\pi\)" pi , o número áureo "\(\varphi\)", além de outras curiosidades como a sequência de Fibonacci.

Ano: 1959 (EUA)
Comentário: esse vídeo mostra de forma lúdica como a matemática está presente na nossa vida. Refere-se ao retângulo de ouro, à sequência de Fibonacci, aos ângulos e de como a geometria está presente na arquitetura, na arte, nos jogos e em várias áreas de conhecimento.
Nesta unidade, você estudou importantes conceitos relacionados à trigonometria, construção gráfica, noções de limites e continuidade de uma função num ponto. Dentre os conceitos da trigonometria, inicialmente, destacamos o estudo do triângulo retângulo mostrando aplicações na resolução de situações problemas relacionados a algumas áreas de conhecimento. Em seguida, apresentamos o estudo do ciclo trigonométrico, que facilita a leitura das relações trigonométricas como seno, cosseno e tangente, dentre outras. Além disso, estudamos as características das funções trigonométricas, como: domínio, imagem, período, paridade e construção gráfica. Finalmente, por meio da construção gráfica de funções definidas por várias sentenças, foi possível entender o conceito de limite e continuidade de uma função num ponto dado.
ANDRADE, A. O. Pitágoras . Disponível em: http://www2.uesb.br/cursos/matematica/matematicavca/wp-content/uploads/cc4.pdf . Acesso em: 27 nov. 2019.
ANTON, H. Cálculo . 10. ed. Porto Alegre: Bookman, 2014. v. 1. ISBN 9788582602263.
COSTA, N. M. L. da. A História da Trigonometria . Disponível em: http://www.ufrgs.br/espmat/disciplinas/geotri/modulo3/mod3_pdf/historia_triogono.pdf . Acesso em: 27 nov. 2019.
DEMANA, F. D. et al . Pré-Cálculo . 2. ed. São Paulo: Pearson Education do Brasil, 2013.
HIBBELER, R. C. Resistência dos Materiais . Local: São Paulo. Pearson, 2009
SANTOS, A. J. de A. 1000 Testes de Matemática . 5. ed. Salvador: Colégio Anchieta, 2005. v. 3.