Circuitos Elétricos I
Conceitos Iniciais de Eletrodinâmica
A engenharia tem como ênfase fazer com que as coisas funcionem, por isso, um engenheiro está livre para utilizar qualquer técnica de qualquer área de atuação para conseguir atingir seu objetivo, o principal é resolver o problema. Essa busca em fazer com que as coisas funcionem tem muito sentido quando pensamos na disciplina de circuitos elétricos, pois ela é o fator comum de todos os campos da engenharia elétrica.
Um circuito elétrico é uma interconexão de elementos elétricos. Tendo isso em mente, começaremos definindo conceitos básicos como grandezas, unidades de medidas, elementos de circuitos, e iniciaremos as análises de circuitos.
Para iniciarmos nossos estudos de circuitos elétricos, precisamos entender os conceitos que serão sua base, envolvendo as principais grandezas e as unidades de medida, como tensão, corrente, potência e energia. Após a apresentação desses conceitos, veremos os elementos de circuitos e a conversão de sinais, como fontes, e a conversão de sinais, que será utilizada para análises futuras. Engenheiros tecnologistas trabalham com quantidades mensuráveis, então, devemos trabalhar com padrões de unidades de medidas para que todos os profissionais independentes do país onde estejam possam entender qual medida foi realizada (SADIKU; MUSA; ALEXANDER, 2014, p. 3).
O Sistema Internacional de Unidades (SI) é usado pela grande maioria dos engenheiros em todo o mundo, e elas são baseadas em sete quantidades definidas, podendo também ser combinadas formando unidades derivadas, tais como força, energia, potência, carga elétrica, entre outras (NILSSON; RIEDEL, 2009, p. 5).
Em muitos casos, a unidade do SI é muito pequena ou muito grande para ser usada em correspondência à sua potência de 10. Engenheiros costumam utilizar apenas os prefixos divisíveis por três (NILSSON; RIEDEL, 2009, p. 5).
Sendo assim, temos as sete principais unidades de medidas no Quadro 1.1, suas derivações no Quadro 1.2 e os prefixos mais utilizados no Quadro 1.3. Essas informações são essenciais para o desenvolver da disciplina, pois são nossa base para mensurar as análises e padronizá-la.
Conhecer as grandezas que serão mensuradas nas análises de circuitos elétricos é extremamente importante, pois devemos manter sempre nossos estudos com uma comunicação clara, de maneira que todos os profissionais consigam compreendê-las.
A carga elétrica é a base para descrever fenômenos elétricos, então, devemos ter em mente que: elas são bipolares (positivo e negativo), existem em cargas discretas múltiplas inteiras de 1,6022 x 10-19C, os efeitos elétricos são atribuídos à separação entre cargas e ao movimento delas (NILSSON; RIEDEL, 2009, p. 7). Segundo Nilsson e Riedel (2009, p. 7), “na teoria de circuitos, a separação entre cargas dá origem a uma força elétrica (tensão), e seu movimento dá origem a um fluxo elétrico (corrente)”.
Sadiku, Musa e Alexander (2014, p. 10) dizem que, para mover um elétron, é necessária a aplicação de uma força eletromotriz (fem) externa. Sendo essa força chamada de tensão, quando falamos sobre uma tensão Vab, estamos nos referindo à energia (ou trabalho) necessária para mover uma carga Q, de um ponto a para o ponto b. Matematicamente temos:
\[Vab=~W/Q~\] (1.1)
Nilsson (2009, p. 7) afirma que “os efeitos elétricos causados por cargas em movimento dependem da variação temporal de carga. Essa variação de cargas é conhecida como corrente elétrica”, sendo expressa pela seguinte equação, em que Q é carga, t, tempo e I, corrente:
\[I=~Q/t\] (1.2)
Esses são conceitos extremamente importantes para nosso estudo de circuitos, pois muitas de nossas análises futuras buscarão encontrar essas grandezas nos circuitos, seja em suas entradas, nas saídas, em elementos específicos ou até desconhecidos dele.
Segundo Sadiku, Musa e Alexander (2014, p. 13), a entrada e a saída de um circuito podem ser expressas em termos de potência e energia. Sendo que a potência e a energia são grandezas totalmente relacionadas à tensão e à corrente.
\[P=~W/t\] (1.3)
Sendo P a potência em watts, W é a energia e t, o tempo.
\[P=~W/t\text{}=~\left( W/Q \right)*\left( Q/t \right)=\text{ }V*I\] (1.4)
Ou
\[P=V*I\] (1.5)
Com isso, vemos que a potência é a relação entre a multiplicação entre tensão e corrente.
Em circuitos elétricos, podemos ter diversos elementos em associação. Esses elementos podem ser resistores, capacitores, fontes de corrente, fontes de tensão, entre outros.
Burian (2006, p. 2) diz que, na análise de circuitos, algumas variáveis podem ser conhecidas: tensões ou correntes das fontes, valores iniciais de tensões em capacitores e correntes em indutores, os quais são chamados de entradas. Mas o objetivo da análise é obter outros valores, chamados de saídas.
Nilsson e Riedel (2009, p. 17) classificam os elementos de um circuito como ativos e passivos. Sendo os elementos ativos dos circuitos aqueles que podem gerar energia elétrica, como as fontes, (tensão e corrente) e elementos passivos aqueles que não são, como resistores, indutores e capacitores.
Para iniciarmos nossos estudos, definiremos alguns conceitos. Uma fonte elétrica é um dispositivo capaz de converter energia não elétrica em energia elétrica, e vice-versa. Um dínamo é uma máquina que converte energia mecânica em elétrica, e vice-versa. Quando um dispositivo funciona no modelo mecânico para elétrico, este é definido como gerador. Quando um dispositivo transforma energia elétrica em energia mecânica, é definido como motor (NILSSON; RIEDEL, 2009, p. 16).
Para a análise de circuitos, foram criadas fontes ideais, sejam elas de corrente ou de tensão. Essas fontes mantêm seu funcionamento de maneira precisa independentemente da variação que possa acontecer nos circuitos (NILSSON; RIEDEL, 2009, p. 16).
Nilsson e Riedel (2009, p. 16) definem fontes ideais de tensão como um elemento do circuito em que a tensão é sempre exata, independentemente da corrente que esteja passando por ela. Fonte ideal de corrente é o elemento análogo ao anterior, mas onde a grande que não varia é corrente, independentemente da tensão aplicada. E essas características não são aplicáveis a elementos reais.
As fontes ideais podem ser descritas como fontes independentes e dependentes. Sendo as independentes aquelas que não dependem da tensão ou da corrente existente em outros pontos do circuito. As dependentes estabelecem seus valores (seja de corrente ou de tensão) dependentes da tensão ou corrente em outro lugar do circuito (NILSSON; RIEDEL, 2009, p. 16).
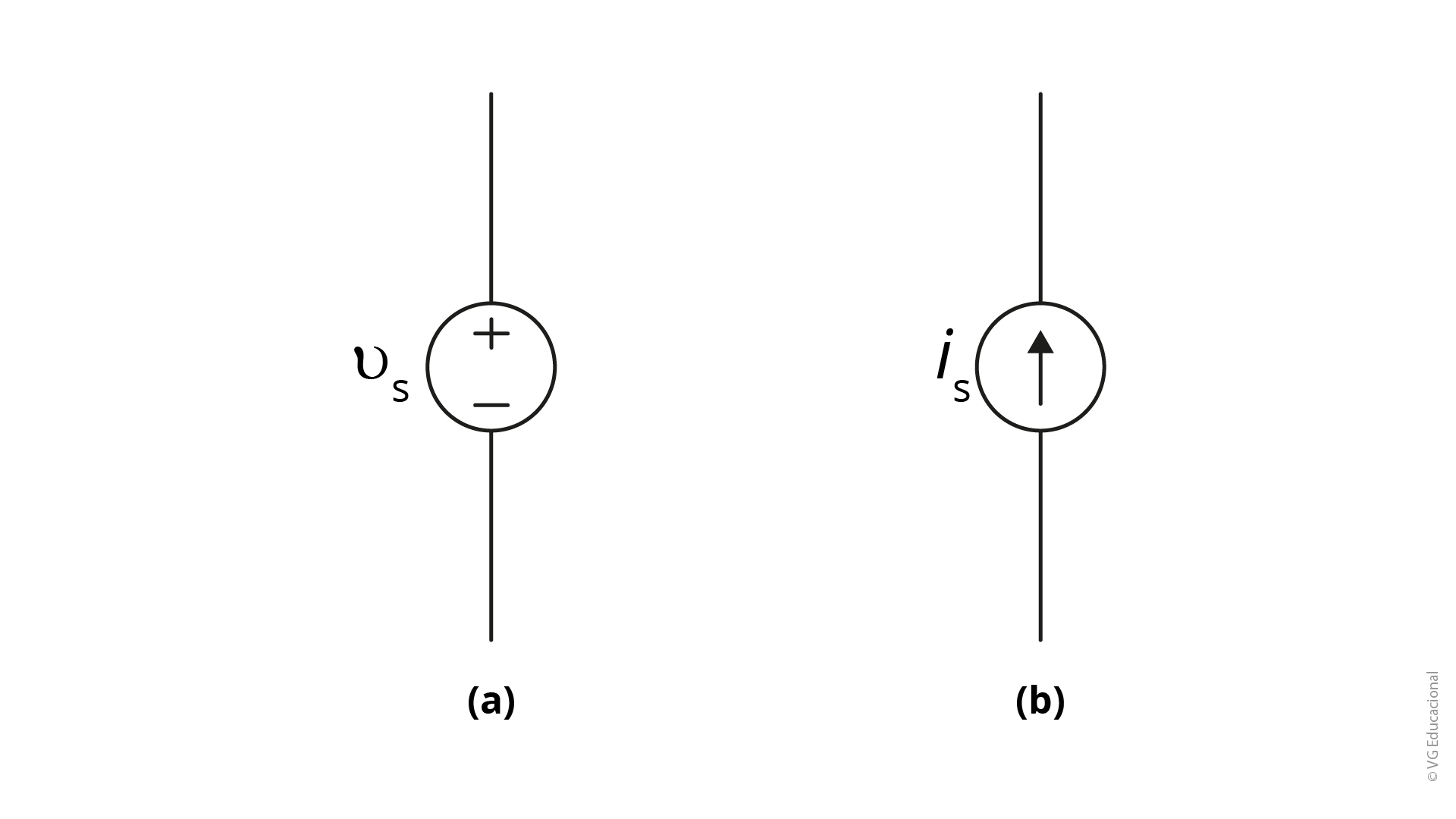
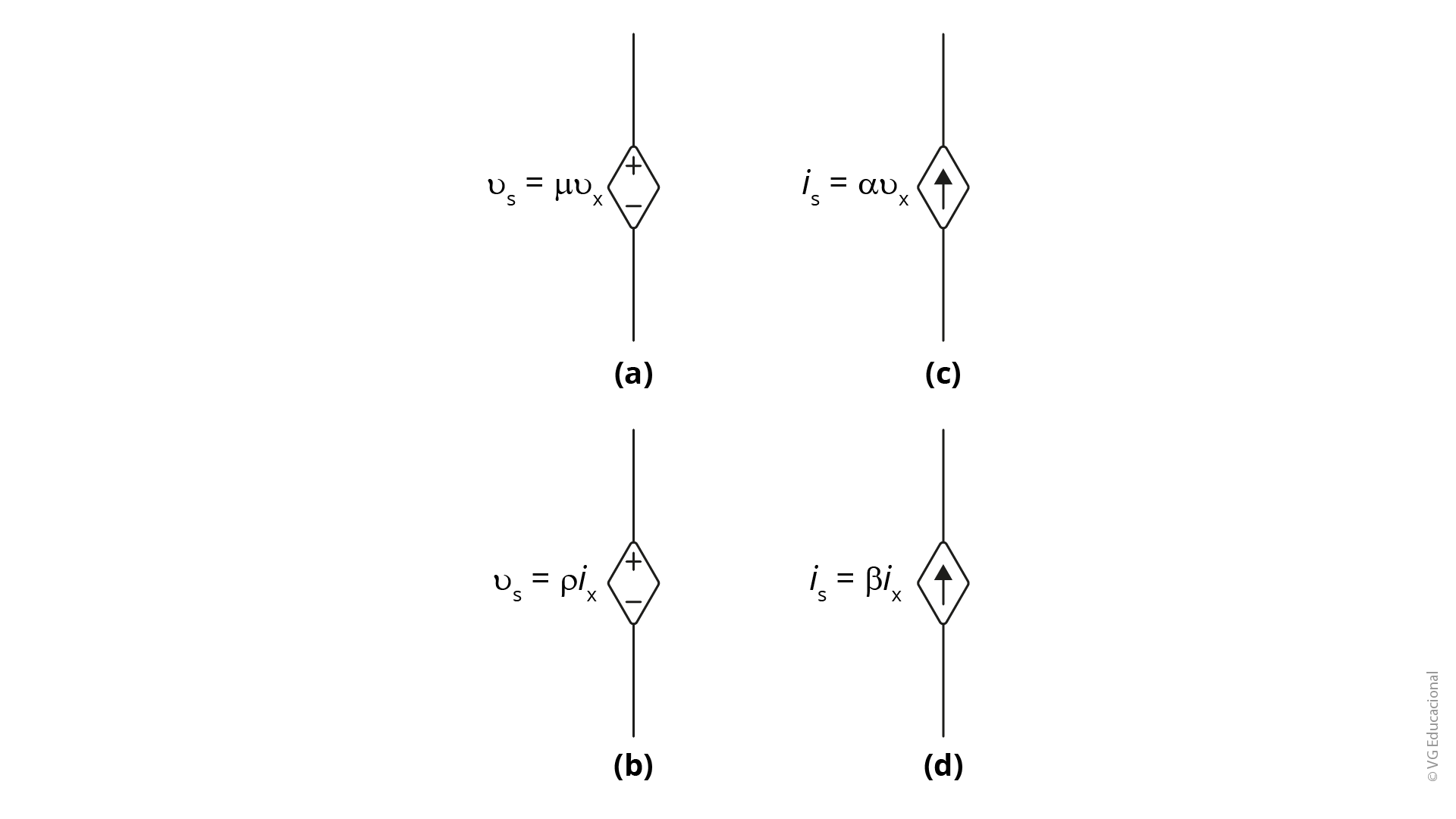
Estes são os quatro tipos de fontes que serão utilizadas em nossos estudos. A compreensão desse elemento de maneira clara auxiliará significativamente quando formos analisar circuitos.
Sadiku, Musa e Alexander (2014, p. 48) dizem que a polaridade da tensão e a direção da corrente tem um papel importante na determinação do sinal da potência. A polaridade da tensão e a direção da corrente devem estar em conformidade com a da Figura 1.3. Isso é conhecido como convenção passiva do sinal. A corrente entra pela polaridade positiva da tensão. Com isso, P = +VI ou VI > 0 significa que o elemento está absorvendo potência, e o contrário significa que ele está fornecendo potência.
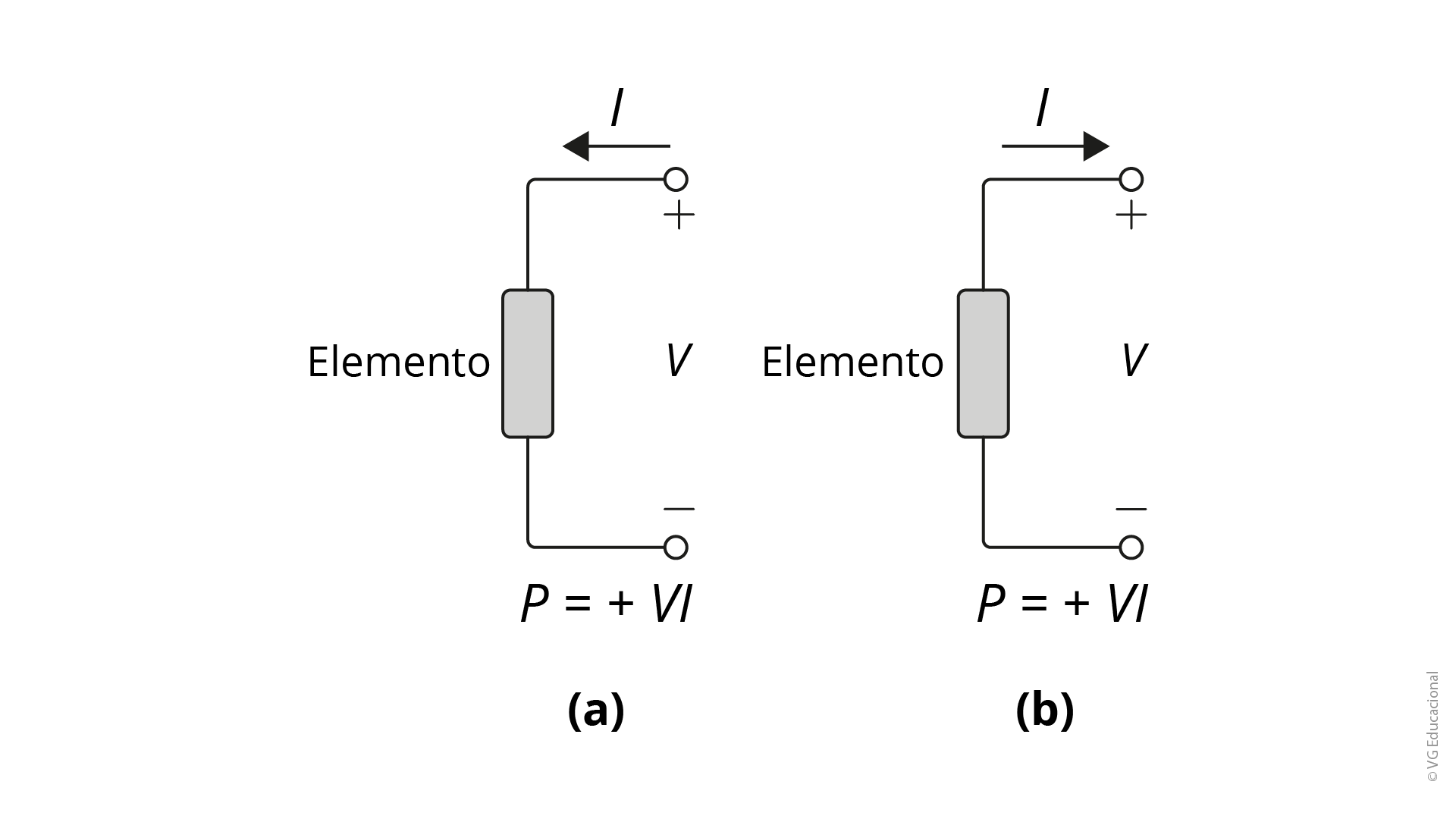
Entender a polaridade da tensão e da corrente em um circuito é essencial para uma análise correta, pois, em diversos circuitos, essas grandezas podem variar (dadas as várias alocações de fontes) mudando a polaridade em alguns ramos.
A representação de grandezas grandes ou pequenas, na engenharia, é feita utilizando as notações científicas. Dessa forma, mantém-se a representatividade dos algarismos significativos, mas ignoram-se os algarismos que não apresentam tanta influência no resultado. Assinale a alternativa que indica a notação de engenharia equivalente ao número 0,0000004587 C.
A grande maioria dos materiais tem um comportamento característico de oposição ao fluxo de carga elétrica. Essa oposição é o resultado das colisões entre elétrons que compõem o material. O símbolo da resistência ou resistor é mostrado na Figura 1.4, na qual R representa a resistência do resistor (SADIKU; MUSA; ALEXANDER, 2014, p. 22).
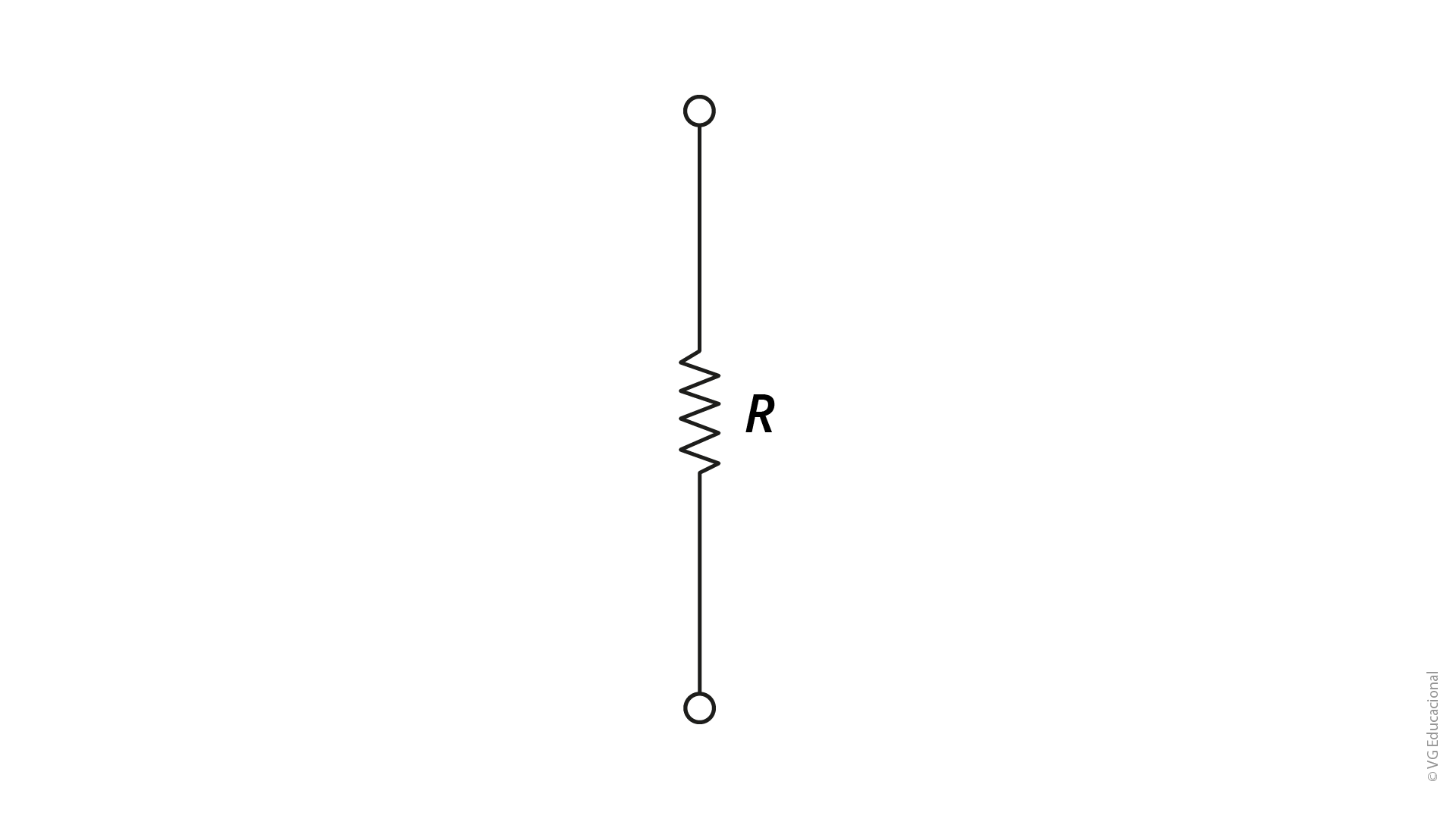
A resistência é expressa em ohms, simbolizada pela letra (Ω). Um exemplo de resistor é a resistência de um chuveiro elétrico.
Nas análises de circuitos, vamos nos referir à corrente e, no resistor, à tensão terminal. Sendo assim, a relação entre a tensão e a corrente é:
\[V\text{ }=\text{}R\text{ }*\text{ }I~\] (1.6)
Onde V é a tensão terminal, R, a resistência e I, a corrente. Esta é a lei de OHM.
O inverso da resistência é definido como condutância, simbolizado pela letra G e medido em Siemens (S).
\[G=\text{ }1/R\text{}\text[S]\] (1.7)
Durante nossas análises, usaremos resistores ideais, adjetivo que nos remete à ideia de que suas propriedades não variam de acordo com o tempo.
A potência desse elemento pode ser expressa de diversas formas, associando as equações 2.1 e 2.2.
\[P=V*I=R*{{I}^{2}}={{V}^{2}}/R\] (1.8)
Independentemente do método utilizado para calcular a potência absorvida por um resistor, o resultado será o mesmo. Quando for realizar uma análise, observe as informações dadas e escolha a equação que utilize essas informações de forma direta.
Observe a análise do circuito da Figura 1.5.
A tensão Va é uma queda na direção do resistor, sendo assim, pela Figura 1.5, temos:
\[Va=\left( 1\right)\left( 8 \right)=8V\]
A potência absorvida pelo resistor, seguindo a Equação 1.8:
\[P=V*I=8*1=8W\]
Com isso, sabemos sobre essas quatro informações sobre esse circuito, tensão no resistor, corrente da fonte, resistência e potência.
A lei de Ohm por si mesma não é suficiente para analisar circuitos. Porém, quando a utilizamos e acrescentamos as duas leis de Kirchhoff, podemos analisar vários circuitos elétricos (SADIKU; MUSA; ALEXANDER, 2014, p. 64).
Antes de falarmos das duas leis de Kirchhoff, definiremos alguns conceitos essenciais para a análise de circuitos, nós e laços (ou caminho fechado).
Um nó é um ponto no qual dois ou mais elementos se unem. Laço é um caminho fechado que começa por um nó, passa pelos elementos básicos do circuito selecionado e retorna ao nó original sem passar por qualquer nó intermediário por mais de uma vez (NILSSON; RIEDEL, 2009, p. 24).
Com esses conceitos, podemos conhecer as duas leis de Kirchhoff:
Na LCK, deve-se definir um sinal algébrico, correspondente à direção de referência para cada corrente no nó. Sendo assim, atribuir um sinal positivo a uma corrente que sai de um nó significa atribuir um sinal negativo a uma corrente que entra em um nó (NILSSON, 2009, p. 24).
A universidade de Colorado tem um simulador de circuitos gratuito. Lá você pode montar seus circuitos e fazer simulações com resistores, chaves, baterias entre outros componentes. Para saber mais, acesse o link a seguir.
Para aplicarmos a LTK, devemos definir um sinal algébrico, referente à direção de referência, a cada tensão do laço. À medida que for traçado um caminho fechado, aparecerá uma queda ou uma elevação de tensão na direção que escolhemos. Sendo assim, atribuir um sinal positivo a uma queda de tensão significa atribuir um sinal negativo à queda de tensão (NILSSON; RIEDEL, 2009, p. 24).
As leis de Kirchhoff nos acompanharão até o fim dos nossos estudos sobre circuitos, logo, uma boa compreensão sobre elas é essencial.
Analise a figura a seguir.

A associação de elementos em série é um dos arranjos básicos na análise de circuitos elétricos. Sabemos que, pela Lei de Kirchhoff das tensões, a soma das tensões no circuito deve ser igual a zero. Sendo assim, para o circuito da figura, encontre os valores de V1 e V2 utilizando a lei de ohm e as leis de Kirchhoff.
Quando trabalhamos com circuitos reais, é necessário fazer medições de tensões, correntes e resistência. Vamos ver quais são os instrumentos que fazem essa medição e como são utilizados.
Vamos ver três instrumentos de medição, para tensão, corrente e resistência, sendo eles voltímetro, amperímetro e ohmímetro. Atualmente, esses instrumentos são combinados em um instrumento conhecido como multímetro, este pode ser analógico ou digital (SADIKU; MUSA; ALEXANDER, 2014, p. 36).
Os medidores analógicos utilizam uma agulha e um medidor calibrado para exibir o valor medido. Os medidores digitais são aqueles cujo valor medido é mostrado sob forma de um mostrador digital (SADIKU; MUSA; ALEXANDER, 2014, p. 36).
Para medir tensão, conectamos o voltímetro/multímetro através do elemento para o qual é desejado se saber a tensão. Sendo assim, este é ligado em paralelo com o elemento conforme a Figura 1.6 a seguir:
Para medir a corrente, conectamos o amperímetro/multímetro em série com o elemento a ser testado. A corrente deve fluir para dentro do instrumento para que ele consiga fazer a medida, conforme a Figura 1.7 a seguir:
Para medir a resistência de um elemento, deve se conectar o ohmímetro/multímetro através dele, como mostrado na Figura 1.8 a seguir:
Estes são equipamentos essenciais nos estudos práticos de circuitos, caso o profissional que esteja fazendo a medição nos componentes a faça de maneira errada, o risco de danificar os equipamentos de medição é alto.
É possível reduzir o número de elementos dentro de um circuito desde que eles sejam da mesma natureza, com isso, diminuímos o número de variáveis do circuito. Dessa maneira, devemos entender a associação de elementos em série e em paralelo.
A associação em série de dois elementos que estão ligados a um único nó é denominada ligação em série. Esses elementos conduzirão a mesma corrente. Dessa maneira, aplicando a lei de Kirchhoff das correntes, conseguimos concluir que, tendo o valor de corrente que está circulando por um dos elementos, sabemos a corrente que está circulando nos outros (NILSSON; RIEDEL, 2009, p. 39).
A associação de paralelo de elementos se dá quando dois elementos estão ligados a um único par de nós. Eles apresentam a mesma tensão em seus terminais (NILSSON; RIEDEL, 2009, p. 39).
As imagens das Figuras 1.9 e 1.10 apresentam associação de resistores, mas podemos fazer a associação de outros elementos também, como fontes, indutores, capacitores, chaves, entre outros.
Resistores em série são frequentemente utilizados para realizar uma divisão de tensão. Desse modo, para determinar a tensão sobre um resistor, observe a Figura 1.11, sabendo que a resistência total da associação em série de resistores é:
\[Req=R1+R2+\cdots+Rn\] (1.9)
A corrente I que flui através dos resistores é:
\[I=~V/Req\] (1.10)
Logo, a tensão em cada elemento é dada por:
\[V1=~R1/Req*V,\text{}V2=~R2/Req*V,\text{ }....\text{ }Vn=~Rn/Req*V\] (1.11)
Onde Rn é o resistor no qual se deseja determinar a queda de tensão, Req é a resistência total dos resistores em série e V é a tensões sobre os resistores em série.
Sendo assim, em um divisor de tensão, a queda de tensão sobre qualquer resistor é proporcional à magnitude de sua resistência.
Um exemplo de elementos ligados em série é um secador de cabelos, onde a resistência e a ventoinha estão conectas dessa maneira.
Para fazer um divisor de tensão, é necessário fazer uma associação em paralelo de resistores.
Sabendo como a tensão e a corrente elétrica se comportam em um circuito onde existe uma associação em série e em paralelo, por que em uma residência as tomadas são ligadas em paralelo e não em série?
A associação de elementos ligados em paralelos tem a mesma tensão em seus terminais. A resistência equivalente entre resistores em paralelos corresponde à seguinte equação:
\[Req=~\left( R1*R2\right)/\left( R1+R2 \right)\] (1.12)
Sendo assim, a associação de dois resistores em paralelo é equivalente ao produto das resistências divididas por sua soma.
Tendo em mente isso para um circuito conforme o da Figura 1.12, vemos que todos os elementos estão sob a mesma tensão V. Sendo a Req a resistência equivalente a:
\[V=It*Req\text{}ou\text{ }It=~V/Req\] (1.13)
Semelhante a isso, temos que:
\[Ix=~Req/Rx\text{}It\] (1.14)
Substituindo a Equação 3.5 em 3.6, temos que:
\[Ix=~Req/Rx\text{}It\] (1.15)
A corrente Ix é o resultado do produto da resistência equivalente Req do circuito dividido pela resistência Rx multiplicada pela corrente do It.
Um exemplo de associação de elementos em paralelo são as tomadas de uma residência, ou, de modo geral, qualquer elemento que necessite receber a mesma tensão que outro.
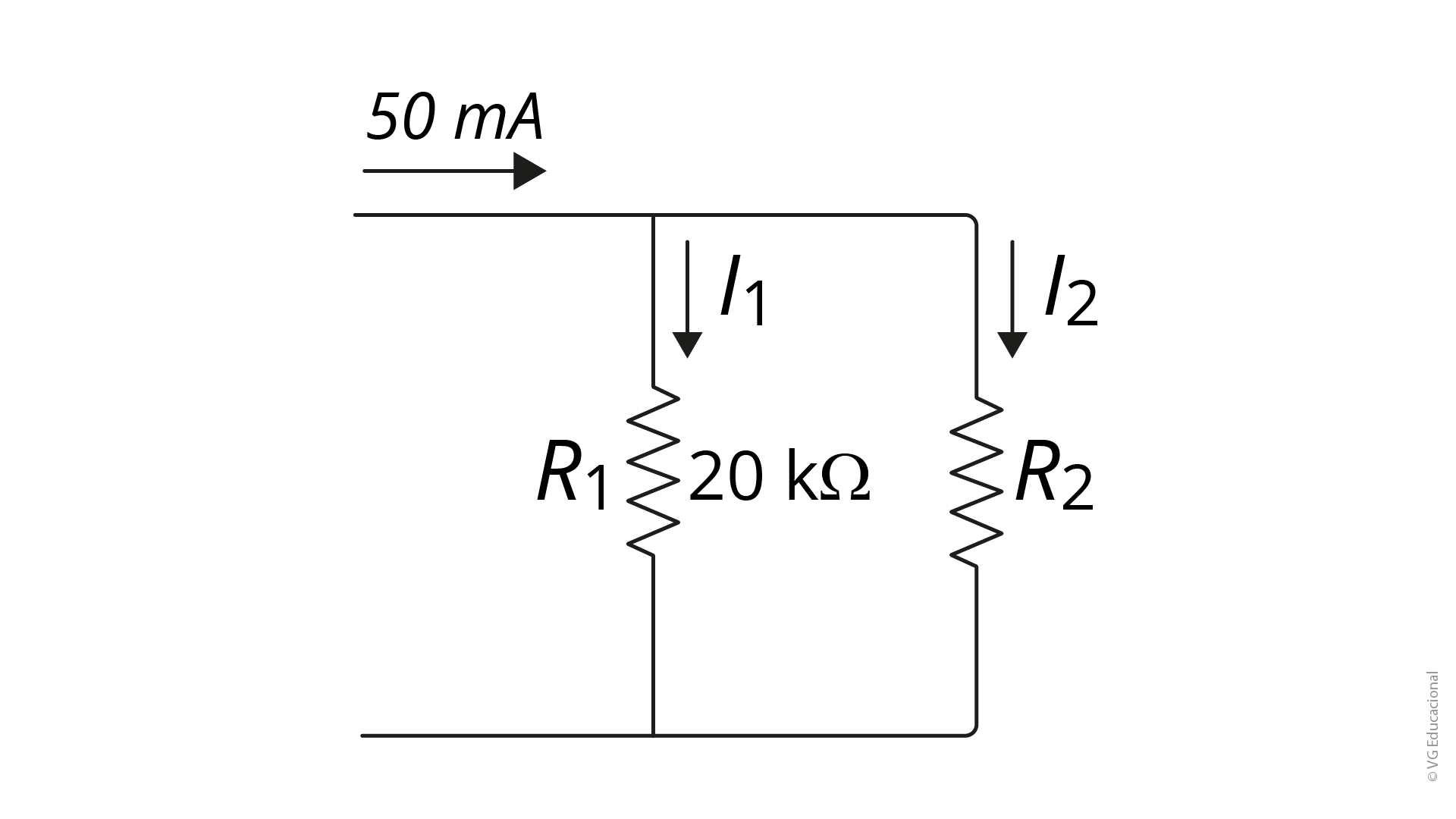
O princípio da divisão de corrente se baseia na aplicação da Lei de Kirchhoff das Correntes, onde é postulado que, para um nó, a soma das correntes que entram deve ser igual à soma das correntes que saem, ou, ainda, que a soma algébrica das correntes em um nó deve ser igual a zero. Sendo assim, analise o circuito da figura a seguir e determine o valor da resistência R2, de modo que a resistência equivalente seja 4 kΩ.
Após compreender as leis fundamentais da teoria de circuitos (Ohm e Kirchhoff), vamos iniciar a aplicação de análises profundas: análise de nodal, que é baseada na aplicação sistemática da Lei de Kirchhoff para Correntes (LKC) e a análise de malhas, que é baseada na aplicação sistemática da Lei Kirchhoff para Tensão (LKT).
A análise nodal aplica a LKC para determinar tensões desconhecidas.
Nessa análise, nosso interesse é encontrar as tensões nodais. Dado um circuito com n nós sem fontes de tensão, a análise nodal de um circuito envolve três passos.
Para iniciar a análise, é necessário selecionar o nó de referência. O nó de referência é chamado de terra, pois ele assume potencial zero. Você determina qual será esse nó.
Uma vez que foi selecionado o nó de referência, atribuímos as tensões dos outros nós. Utilizaremos a Figura 1.13 (a) como exemplo. O nó 0 é a referência (V = 0V), enquanto aos nós 1 e 2 são atribuídas as tensões V1 e V2, respectivamente. Lembrando que a tensão de nó é definida tendo como referência o nó escolhido.
No segundo passo, aplicamos a LKC para cada nó do circuito, com exceção do nó de referência. Para facilitar a interpretação, reescrevemos o circuito na Figura 1.13 (b).
Aplicando a LKC no nó 1, temos
\[Is1=Is2+I1+I2~\] (1.16)
No nó 2, temos
\[Is2+I2=I3\] (1.17)
Agora, aplicando a lei de Ohm, para encontrar as correntes desconhecidas, em termos das tensões nodais, I1, I2 e I3.
\[I=Valto-VbaixoR\] (1.18)
Com isso, temos que:
\[I1=~\left( V1\text{ }-0 \right)/R1~\] ou \[I1=G1V1\]
\[I2=~\left( V1\text{ }-V2 \right)/R2~\] ou \[I2=G2\left( V1-V2 \right)\] (1.19)
\[I3=~\left( V2\text{ }-0 \right)/R3~\] ou \[I3=G3V2\]
Substituindo as equações (1.19) em (1.17) e (1.18), temos os seguintes resultados, respectivamente:
\[Is1=Is2+~V1/R1+\left(V1-V2 \right)/R2\] (1.20)
\[Is2+~\left( V1-V2\right)/R2=~V2/R3\] (1.21)
Podemos também fazer a substituição em termos da condutância.
O terceiro passo na análise nodal é resolver as equações para as tensões nodais. Se aplicarmos a LKC para N-1 nós, teremos n-1 equações simultâneas, como as equações 1.19 e 1.20. Para obtermos as tensões nodais V1 e V2, da Figura 1.13, podemos utilizar qualquer método padrão, como o método da substituição, o da eliminação, a regra de Cramer ou a inversão de matriz.
Para iniciarmos a análise de malhas, precisamos entender a definição de malha. Uma malha é um laço que não contém qualquer outro laço dentro dele.
Na análise de malha, estamos interessados em aplicar a LKT para encontrar a corrente de malha em um determinado circuito. Sendo assim, a análise de malha segue três passos:
Para ilustrar o método, vamos utilizar na análise o circuito da Figura 1.14. O primeiro passo requer que as correntes de malhas i1 e i2 sejam atribuídas às malhas 1 e 2.
No segundo passo, ao aplicar LKT nas malhas 1 e 2, temos, respectivamente:
\[-V+R1i1+R3\left(i1-i2 \right)=0\] (1.22)
\[R2i2+V2+R3\left(i2-i1 \right)=0\] (1.23)
O terceiro passo é determinar a corrente de malha. Colocando na forma matricial, temos:
\[\left[ \begin{matrix} R1+R3 & -R3\\-R3 & R2+R3 \\\end{matrix} \right]\left[ \begin{matrix}i1\\i2 \\\end{matrix} \right]=\left[ \begin{matrix}V1\\-V2\\\end{matrix} \right]\] (1.24)
Com isso, se tem liberdade para o emprego de qualquer técnica para solução de equações simultâneas a fim de se obter os valores i1 e i2.
Observando a figura, fica claro que:
\[I1\text{ }=\text{}i1,\text{ }I2\text{ }=\text{ }i2,\text{ }I3\text{ }=\text{ }i1-i2\] (1.25)
Dessa maneira, é possível fazer uma análise de malhas em circuitos com essas características.
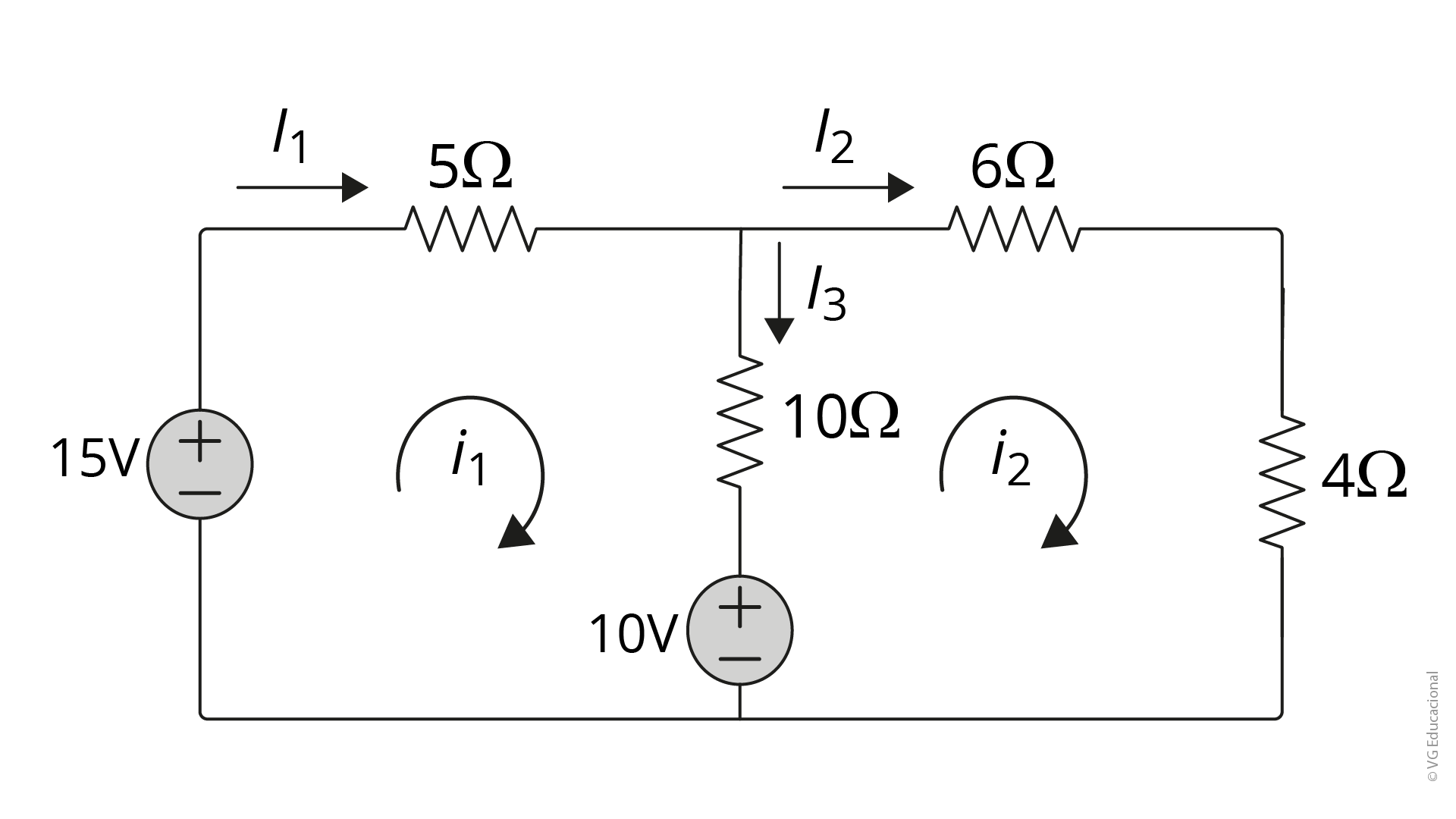
A análise de malhas é uma técnica muito poderosa para analisar circuitos, proveniente da aplicação das Leis de Kirchhoff das Correntes e das Tensões. Por meio dela, podemos obter todas as grandezas vigentes em um circuito. Dito isso, analise a figura a seguir e determine as correntes I1, I2 e I3 usando a análise de malha.
Assinale a alternativa correta.

Ano: 2017
Comentário: É possível ver a batalha entre Thomas Edison e George Westinghouse sobre como deveria ser feita a distribuição da energia elétrica, em corrente contínua ou corrente alternada, filme que ilustra temas que estudamos nesta unidade. Para conhecer mais sobre o filme, acesse o trailer em:

Editora: Pearson
Autora: James W. Nilsson
Comentário: O livro trabalha o tema circuitos elétricos de maneira clara e bem exemplificada, trazendo o passo a passo e os detalhes essenciais para o estudo de circuitos elétricos, fazendo ligação com temas propostos e apresentados nesta unidade.
Nesta unidade foi possível conhecer melhor os circuitos elétricos, seus principais fundamentos, a Lei de Ohm e as leis de Kirchhoff de tensão e corrente, além dos instrumentos de medidas necessários para fazer a medição das grandezas em circuitos. Sendo assim, já temos uma boa base para avançar nas análises de circuitos aplicando os fundamentos e as análises mais complexas como a análise nodal, que é voltada para encontrar as tensões desconhecidas de um circuito, e a análise de malhas, voltada a encontrar as correntes de malhas. Com isso, podemos notar que todos os conceitos abordados até os momentos são fundamentais e úteis em toda a análise de circuito, desde o mais simples até os mais complexos.
BURIAN JR., Y.; LYRA, A. C. C. Circuitos elétricos . São Paulo: Prentice-Hall, 2006.
NILSSON, J. W.; RIEDEL, S. A. Circuitos elétricos . 8. ed. São Paulo: Pearson Prentice Hall, 2009.
SADIKU, M. N. O.; MUSA S. M.; ALEXANDER, C. K. Análise de circuitos elétricos com aplicações . 5. ed. São Paulo: Editora AMGH, 2014.