Circuitos Elétricos I
Circuitos de Primeira Ordem
Conhecemos dispositivos que armazenam energia, indutores e capacitores. Agora vamos determinar as tensões e correntes que surgem quando a energia é fornecida ou recebida a um desses componentes quando ocorre uma variação abrupta em uma fonte de corrente ou tensão de corrente contínua. Abordaremos circuitos formados por apenas resistores e indutores ou capacitores, mas não ambos. Essas configurações são denominadas circuitos RC, resistor-capacitor e RL, resistor-indutor.
Nossa análise abordará primeiramente uma resposta natural do circuito. Em um segundo momento, consideramos a resposta ao degrau.
Os circuitos são considerados de primeira ordem, porque possuem apenas um armazenador de energia; sendo assim, suas tensões e correntes são descritas por equações diferenciais de primeira ordem.
Circuitos de primeira ordem são circuitos compostos por apenas um tipo de dispositivo armazenador de energia (indutores e capacitores); sendo assim, suas equações de tensão e correntes são compostas por derivadas de primeira ordem.
Vamos trabalhar com circuitos compostos por resistores e capacitores (circuitos RC).
Para Nilsson (2009), a resposta natural de um circuito RC pode ser descrita conforme a Figura 3.1. Iniciaremos nossa análise fazendo a suposição de que a chave estava na posição a por um longo período de tempo, o que permite considerar que o ramo formado pela fonte de tensão de corrente contínua \({{V}_{g}}\), o resistor \({{R}_{1}}\) e o capacitor C cheguem a uma condição de regime permanente. Sabe-se que um capacitor tem o comportamento equivalente a um circuito aberto quando está associado a uma tensão constante. Logo, a tensão nos terminais do capacitor é equivalente à da fonte. Quando a chave é comutada da posição a para a posição b (em t=0), a tensão nos terminais do capacitor não pode sofrer variação instantânea, então, o problema se reduz ao circuito mostrado na Figura 3.2.
Para determinar a tensão v(t), fazemos uma análise em termos de tensões de nó. Utilizando o nó inferior entre R e C como o nó de referência e somando as correntes que saem da junção superior entre R e C, fazendo a análise matemática, chegamos à seguinte equação:
\[v(t)=v(0){{e}^{(-t/(RC)}}\] (3.1)
para t maior ou igual a zero.
A tensão imediatamente antes, durante e depois do momento t = 0 é igual à tensão \({{V}_{g}}\), equivalente à tensão \({{V}_{0}}\).
A relação de RC equivale à constante de tempo. Sadiku, Musa e Alexander (2014) considera a constante de tempo, sendo esta mensurada em segundos, onde τ de um circuito é o tempo necessário para a resposta (corrente) diminuir de um fator de 36,8% do seu valor inicial.
Conforme Nilsson (2009), a constante de tempo é um parâmetro importante para circuitos de primeira ordem, sendo ela a resposta transitória do circuito, pois é o tempo necessário de que o circuito necessita para atingir o seu estado final.
Dessa maneira, a equação correspondente à constante de tempo em um circuito RC é dada pela multiplicação da resistência R pela capacitância C:
\[\tau =RC\] (3.2)
Logo, a Equação 3.1 pode ser reescrita como:
\[v\left( t \right)=v\left( 0 \right){{e}^{-t/\tau }}\] (3.3)
O que representa que a resposta natural de um circuito RC é uma queda de tensão exponencial a partir da tensão inicial.
Sendo τ a constante que determina a velocidade da queda, a Figura 3.3 representa o gráfico da Equação 3.3.
Analisando a Figura 3.3, vemos o comportamento da exponencial negativa, sendo que a mesma parte do valor inicial da tensão e tende a zero, tendo a sua inclinação dada pelo valor da constante de tempo, que é resultado dos valores de resistência e capacitância do circuito.
Sendo o pisca alerta um chaveamento exemplo de chaveamento sequencial, como dimensionar a constante de tempo para um circuito como este?
Após determinarmos v(t), podemos determinar a corrente i, potência p, e a energia w.
\[i\left( t \right)=\frac{v\left( t \right)}{R}{{e}^{-t/\tau }}\] (3.4)
\[p=vi=\frac{v{{(0)}^{2~}}}{R}{{e}^{-2t/\tau }}\] (3.5)
\[w=\frac{1}{2}Cv{{(0)}^{2~}}\left( 1-{{e}^{-t/\tau }} \right)\] (3.6)
Para t maior ou igual a zero.
Sendo assim, o cálculo da resposta natural de um circuito RC pode ser resumido da seguinte forma, segundo Nilsson (2009):
Seguindo essa sequência, é possível determinar o valor da tensão em função do tempo.
Ao se tratar da resposta ao degrau de um circuito de primeira ordem, estamos nos referindo à aplicação repentina de uma fonte de tensão ou corrente constante no circuito. Sendo assim, vamos analisar como o circuito responde quando a energia está sendo armazenada no dispositivo (Nilsson, 2009, p. 168).
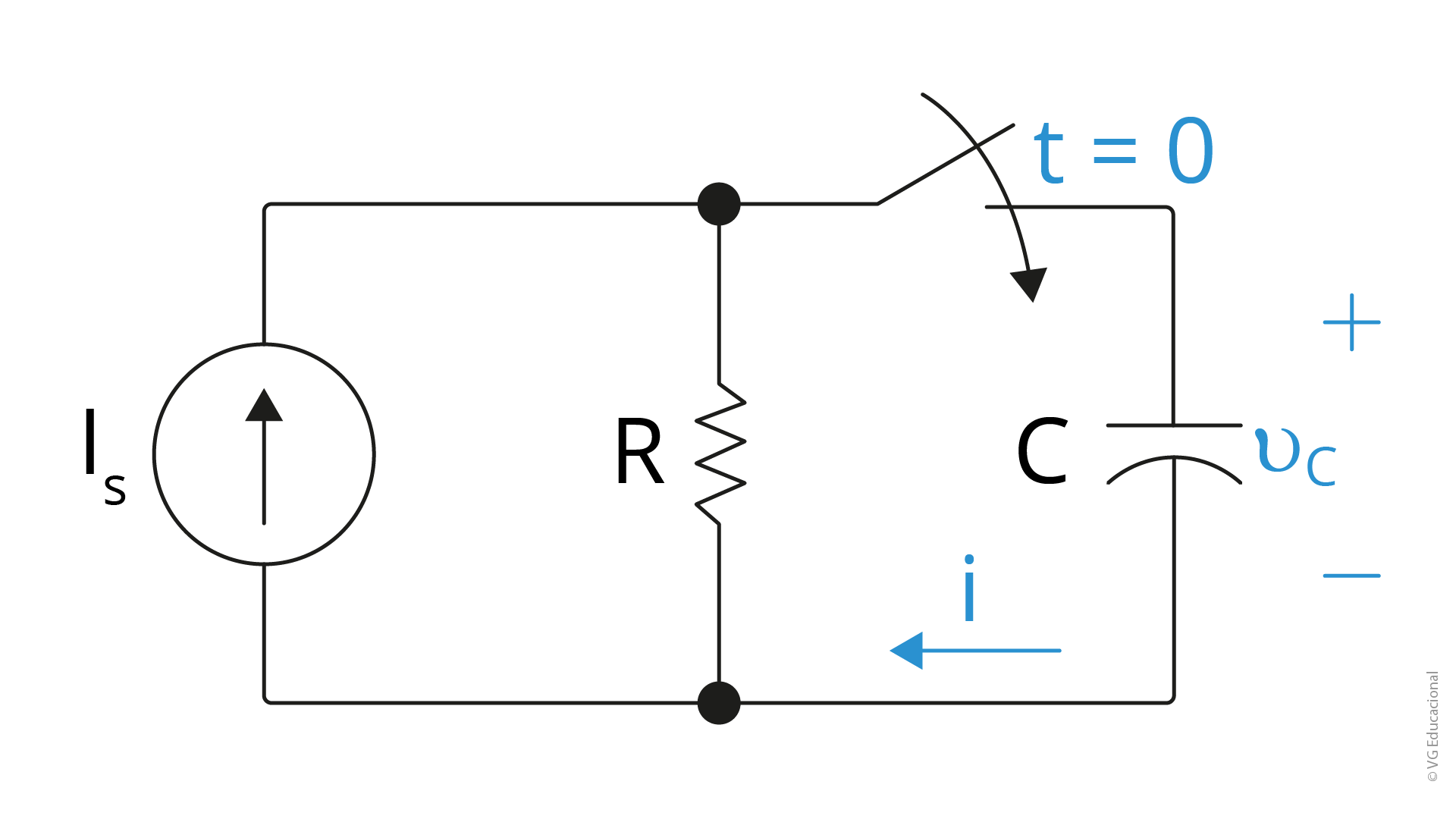
Podemos determinar a resposta a um degrau de um circuito RC, segundo Nilsson (2009), analisando a Figura 3.4. Dessa maneira, escolhemos o equivalente de Norton da rede ligada ao capacitor equivalente. Fazendo a análise matemática, temos:
\[{{v}_{C}}\left( t \right)={{I}_{s}}R+(v\left( 0 \right)-{{I}_{s}}R){{e}^{-t/\tau }}\] (3.7)
para t maior ou igual a zero.
Para determinar a corrente no capacitor, damos sequência à análise e chegamos à seguinte equação:
\[i=\left( {{I}_{s}}-\frac{v\left( 0 \right)}{R} \right){{e}^{-t/\tau }}\] (3.8)
para t maior igual a zero.
Observando a Equação 3.7, vemos que a tensão inicial do capacitor é \({{V}_{0}}\); a tensão final é \({{I}_{s}}R\); e a constante de tempo do circuito é RC. Essas observações são válidas para o comportamento de um capacitor em parelho com um resistor quando alimentados por uma fonte de cc.
A Equação 3.8 prevê que a corrente no capacitor logo após o instante em que o valor de t é igual a zero é \({{I}_{s}}-\left( V0/R \right)\), o que faz sentido, pois a tensão no capacitor não pode variar instantaneamente.
Dentre as várias aplicações de um circuito RC, como circuitos de retardo e relés, uma delas está mais próxima de você do que você imaginava, o flash de uma câmera fotográfica. Para saber mais como funciona esse mecanismo acesse o link a seguir.
Sadiku, Musa e Alexander (2014) afirmam que existem várias aplicações para circuitos de primeira ordem, sendo eles filtragem em fontes de alimentação de corrente contínua, circuitos de suavização para comunicação digital, entre outras. Logo, podemos começar a compreender o quão importante uma boa compreensão do tema é essencial para o desenvolvimento profissional.
Analise a figura a seguir.
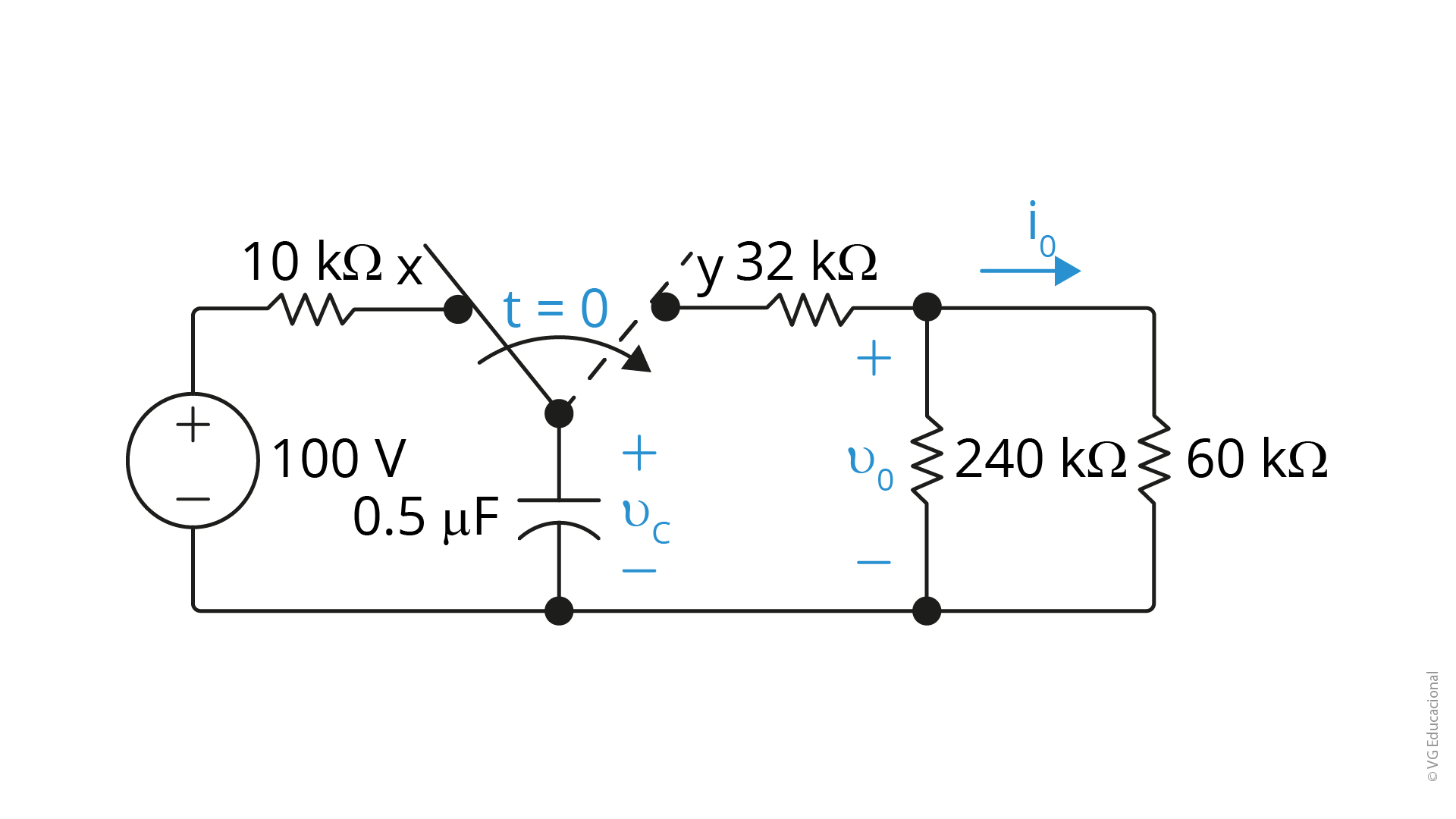
A resposta ao degrau de um circuito é muito utilizada para modelar comportamento de carga e descarga de um circuito RC. A chave do circuito da figura apresentada esteve na posição c por um longo período. No instante em que t é igual a zero, ela passa instantaneamente para a posição y. Desse modo, assinale a alternativa que apresenta o valor de Vc(t) para t maior igual a zero.
Os circuitos de primeira ordem são aqueles em que suas equações são compostas por equações diferenciais de primeira ordem. Assim, sendo compostos por apenas um tipo de dispositivos armazenadores de energia (indutores e capacitores), vamos trabalhar com circuitos compostos por resistores e indutores (circuitos RL).
Para Nilsson (2009), a resposta natural de um circuito RL pode ser descrita conforme a Figura 3.6. Para iniciar nossa análise, começaremos supondo que a chave está na posição a por um longo tempo, o que permite que o laço formado pela fonte de tensão de corrente contínua \({{V}_{g}}\),o resistor R1 e o indutor L cheguem a uma condição de regime permanente. Sabendo o elemento armazenador de energia indutivo tem comportamento equivalente a um curto circuito na presença de uma corrente constante, podemos concluir que a tensão nos terminais do indutor é nula. Quando a chave é comutada da posição a para a posição b (em t=0), a corrente nos terminais do indutor não pode sofrer variação instantânea, logo o problema se reduz ao circuito mostrado na Figura 3.7.
Para determinar a corrente i(t), fazemos uma análise em termos da lei das tensões de Kirchhoff. Somando as tensões ao longo do caminho fechado e fazendo as simplificações matemáticas, chegamos à seguinte equação.
\[i\left( t \right)=i\left( 0 \right){{e}^{-tR/L}}\] (3.9)
para todos os valores de t maior ou igual a zero.
A corrente imediatamente antes, durante e depois do momento t = 0 é igual à corrente Is .
Dessa maneira, a equação correspondente à constante de tempo em um circuito RL é dada pela divisão da indutância L pela resistência R.
\[\tau =L/R\] (3.10)
Logo, a Equação 3.9 pode ser reescrita como:
\[i\left( t \right)=i\left( 0 \right){{e}^{-t/\tau }}\] (3.11)
O que representa que a resposta natural de um circuito RL é uma queda de corrente exponencial a partir da corrente inicial. Sendo τ a constante que determina a velocidade da queda. A Figura 3.8 representa o gráfico da equação 3.11.
Após determinarmos i(t), podemos determinar a tensão v, potência p e a energia w, como:
\[v\left( t \right)=I\left( 0 \right)R{{e}^{-t/\tau }}\] (3.12)
\[p=vi=I{{(0)}^{2~}}R{{e}^{-2t/\tau }}\] (3.13)
\[w=\frac{1}{2}LI{{(0)}^{2~}}\left( 1-{{e}^{-2t/\tau }} \right)\] (3.14)
para todo t maior ou igual a zero.
Sendo assim, o cálculo da resposta natural de um circuito RL pode ser resumido da seguinte forma, segundo Nilsson (2009):
Seguindo essa forma, é possível determinar o valor da tensão em função do tempo.
A resposta ao degrau de um circuito RL é análoga à de um circuito RC, logo não faremos definições redundantes neste tópico.
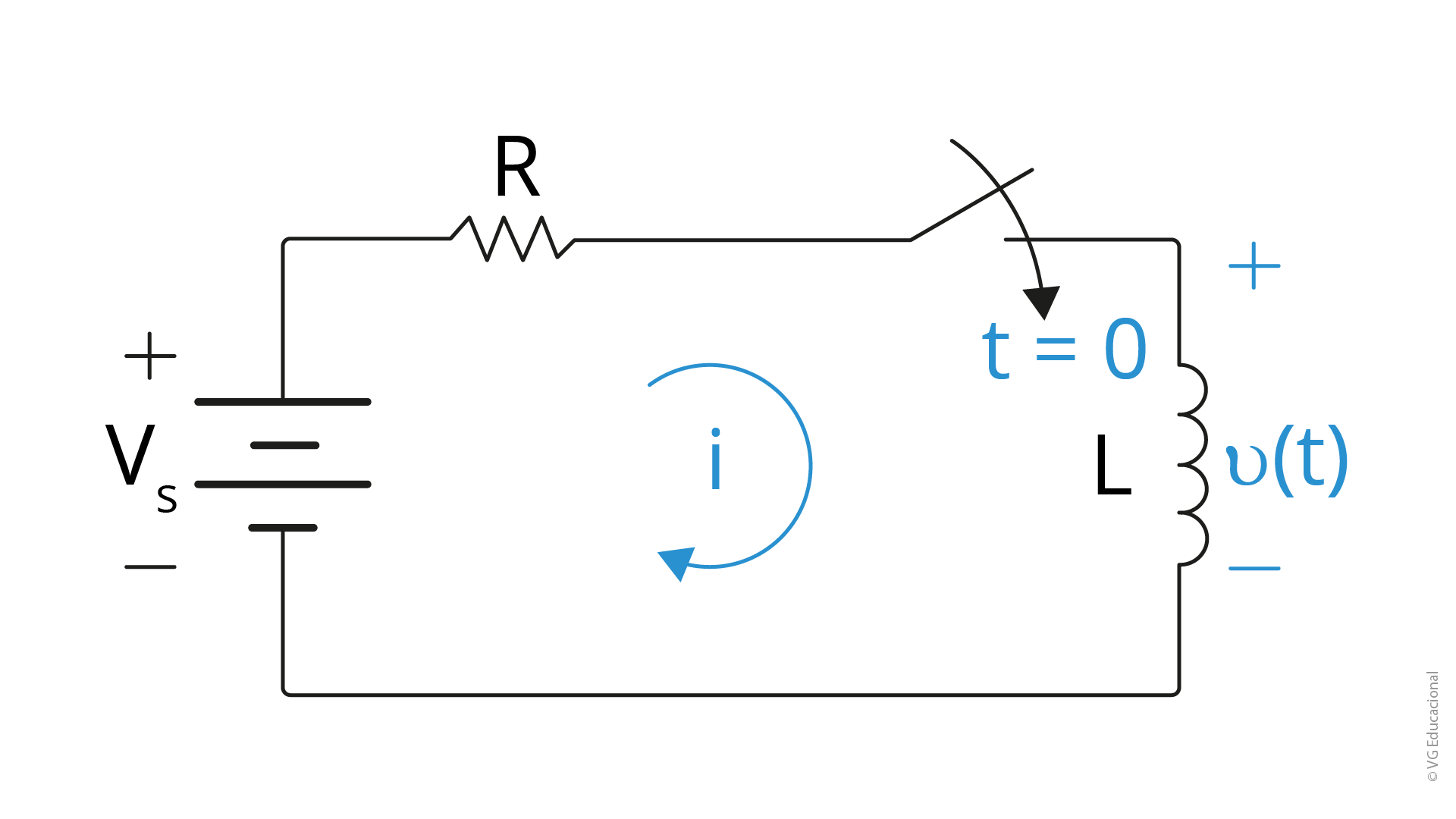
Podemos determinar a resposta a um degrau de um circuito RL, segundo Nilsson (2009) analisando a Figura 3.8. Dessa maneira, escolhemos a lei das tensões de Kirchhoff. Fazendo a análise matemática, temos:
\[i\left( t \right)=\frac{{{V}_{s}}}{R}+\left( I\left( 0 \right)-\frac{{{V}_{s}}}{R} \right){{e}^{-tR/L}}\] (3.15)
para todos os valores de t maior ou igual a zero.
Para determinar a tensão no indutor, damos sequência à análise e chegamos à seguinte equação:
\[v=L\left( \frac{-R}{L} \right)\left( I\left( 0 \right)-\frac{{{V}_{s}}}{R} \right){{e}^{-tR/L}}=({{V}_{s}}-I\left( 0 \right)R){{e}^{-tR/L}}\] (3.16)
para todos os valores de t maior ou igual a zero.
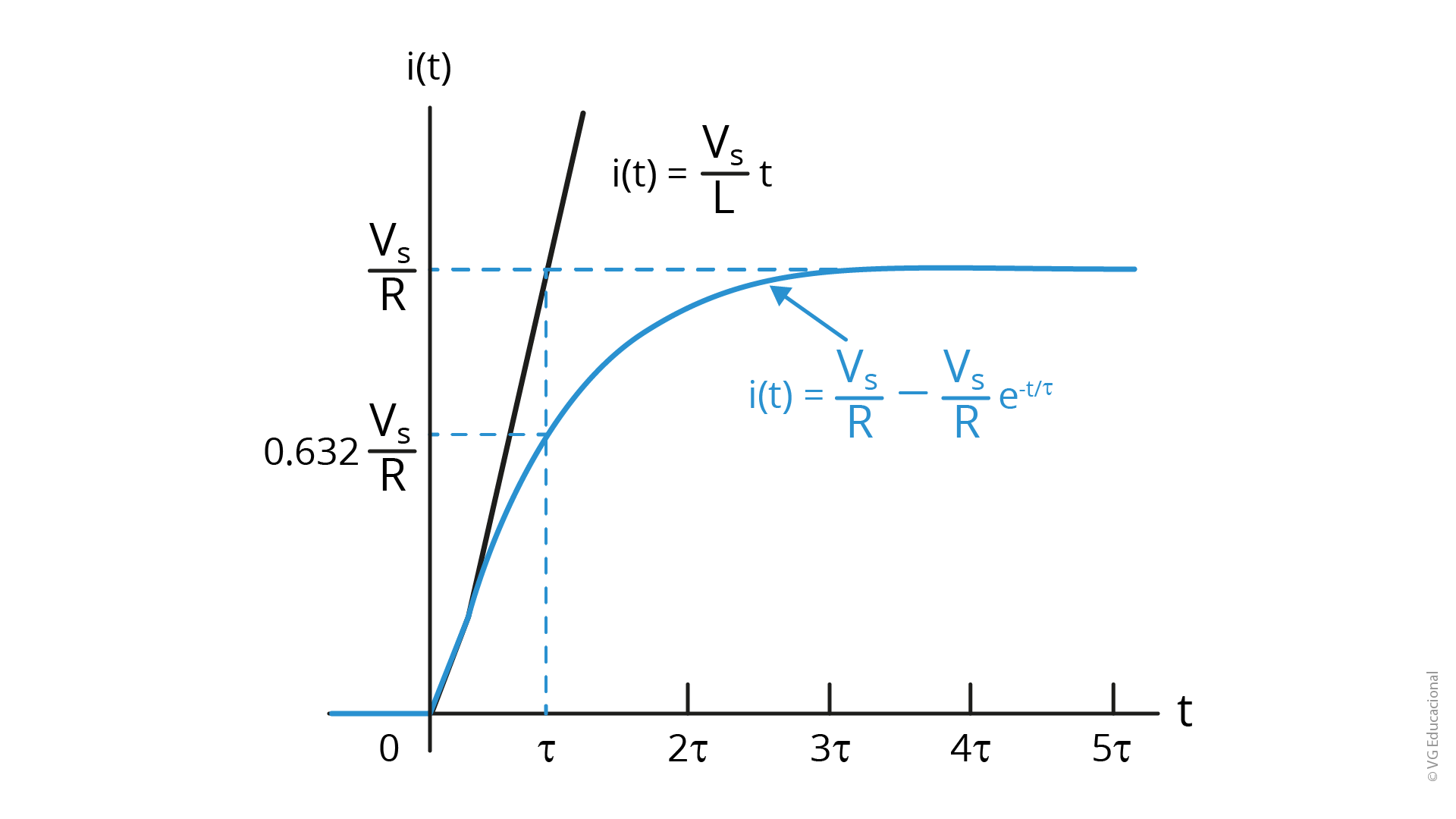
Vemos, dessa forma, que a corrente, em um circuito RL, apresenta a mesma forma de onda da tensão em um circuito RC. Analisando o gráfico, vemos que o carregamento do componente é uma exponencial, com inclinação dada pela constante de tempo, partindo do zero e chegando às grandezas equivalentes às da fonte.
Analise a figura a seguir.
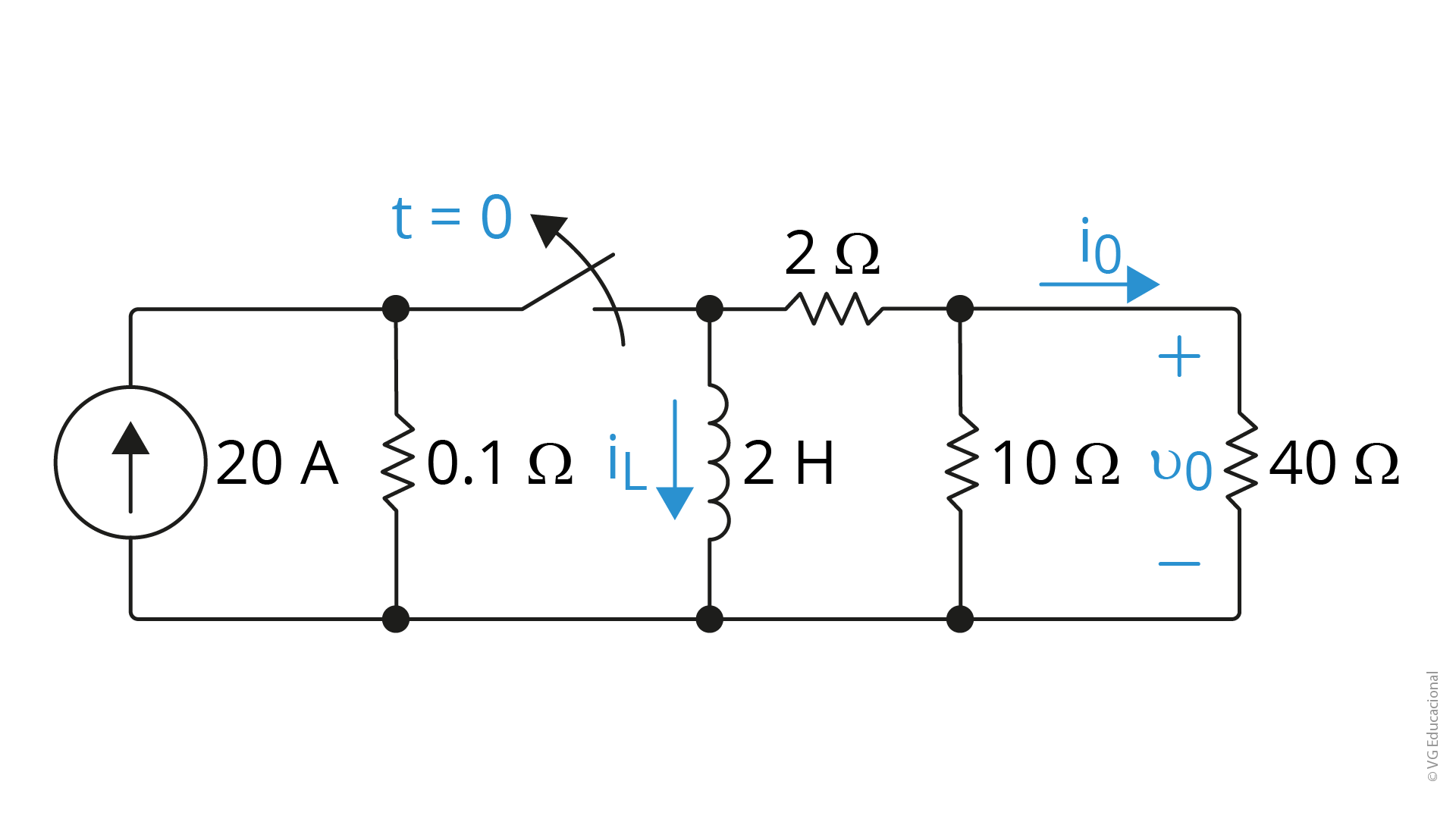
A chave do circuito da figura apresentada esteve na posição a por um longo período. No instante em que t é igual a zero, ela passa instantaneamente para a posição b. Desse modo, assinale a alternativa que apresenta o valor de iL(t) para t maior ou igual a zero.
Circuitos RC e RL respondem de maneira muito similar em seu comportamento em regime transitório e em regime permanente, levando em consideração cada uma de suas particularidades. Visto isso, vamos entender como fazer a análise quando o chaveamento é sequencial, quando existe uma resposta indefinidamente crescente e curva de carga e descarga dos elementos armazenadores de energia.
Nilsson (2009) afirma que chaveamentos que ocorrem mais de uma vez em um circuito são chamados de chaveamento sequencial. Um exemplo é uma chave de duas posições que faz a comutação de maneira sequencial. Sendo assim, a referência para todos os chaveamentos não pode ser t = 0. Determinamos as tensões e correntes geradas, utilizando as técnicas já apresentadas, e a cada novo sequenciamento usamos as expressões de tensão e corrente do circuito para determinar as condições iniciais da próxima condição.
Visto que o valor da constante de tempo não irá alterar, porque seu valor depende dos elementos do circuito, temos que sempre fazer uma atualização do valor inicial da comutação seguinte.
Um exemplo de circuito de chaveamento sequencial é a luz de pisca alerta de um automóvel, no qual a chave comuta sequencialmente.
Nilsson (2009) define que uma resposta indefinidamente crescente é aquela em que o valor da resposta do circuito, em vez de decrescer com o tempo, cresce de maneira indefinida. Essa situação se torna possível quando o circuito em questão apresenta fontes dependentes. Dessa maneira, a resistência, quando vista dos terminais dos elementos armazenadores de energia (sejam eles o indutor ou o capacitor), no equivalente de Thévenin, é negativa, sendo a constante de tempo negativa. Com o passar do tempo, a resposta alcança um valor limite em que o componente é destruído ou entra em um estado de saturação que impede qualquer aumento adicional dessas grandezas.
Para solucionar circuitos assim, derivamos a equação diferencial que descreve o circuito (que possui a resistência negativa) e resolvemos a mesma utilizando a técnica da separação de variáveis.
Um circuito capaz de resultar em correntes e tensões sempre crescentes é um fator importante para engenheiros, porém, se essa situação acontecer de maneira não intencional, o circuito corre sérios riscos de apresentar falhas, gerando um grande risco.
A fim de compreendermos melhor a relação da constante de tempo em um circuito, vamos observar a curva de carga e descarga dos elementos armazenadores de energia.
Dado um circuito conforme a Figura 3.11, assumindo que a tensão vc no momento inicial é zero:
O gráfico de carga do circuito de carga do capacitor é dado pela Figura 3.12, sendo que a carga máxima do capacitor se dá quando vc se torna equivalente a \({{V}_{s}}\).
Retirando a fonte do circuito da Figura 3.11 e assumindo que o capacitor se encontra em carga máxima no momento inicial, temos um circuito de descarga, conforme a Figura 3.13.
Sendo assim, o gráfico de descarga do circuito, dada algumas variações na constante de tempo, pode ser expresso pela Figura 3.14.
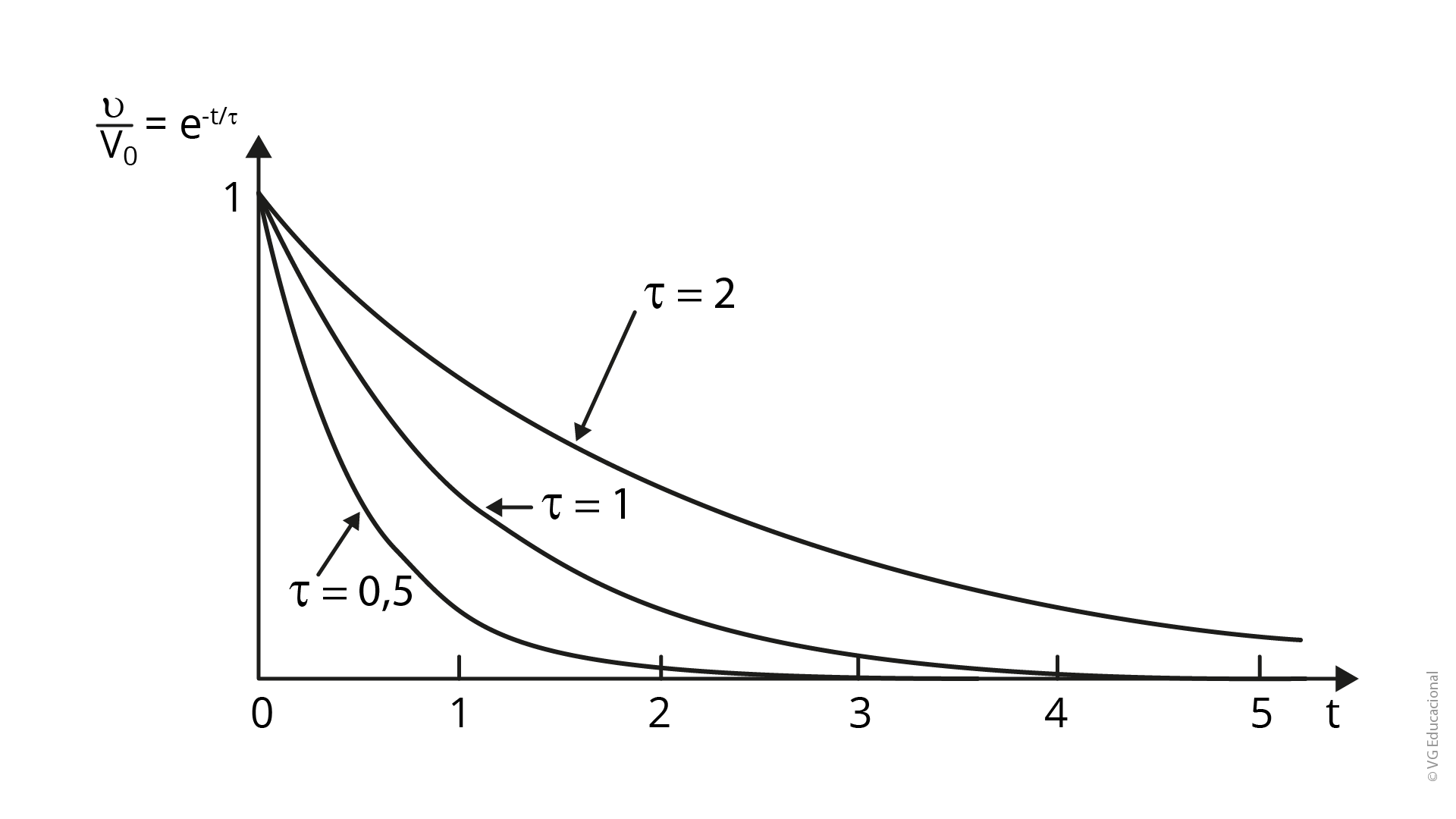
Sabendo que capacitores e indutores se comportam de maneira análoga, dadas a tensão e a corrente, assume-se que esse comportamento de carga e descarga ocorre também em um indutor, considerando que os gráficos apresentados serão para a corrente nesse componente.
Analise a figura a seguir.
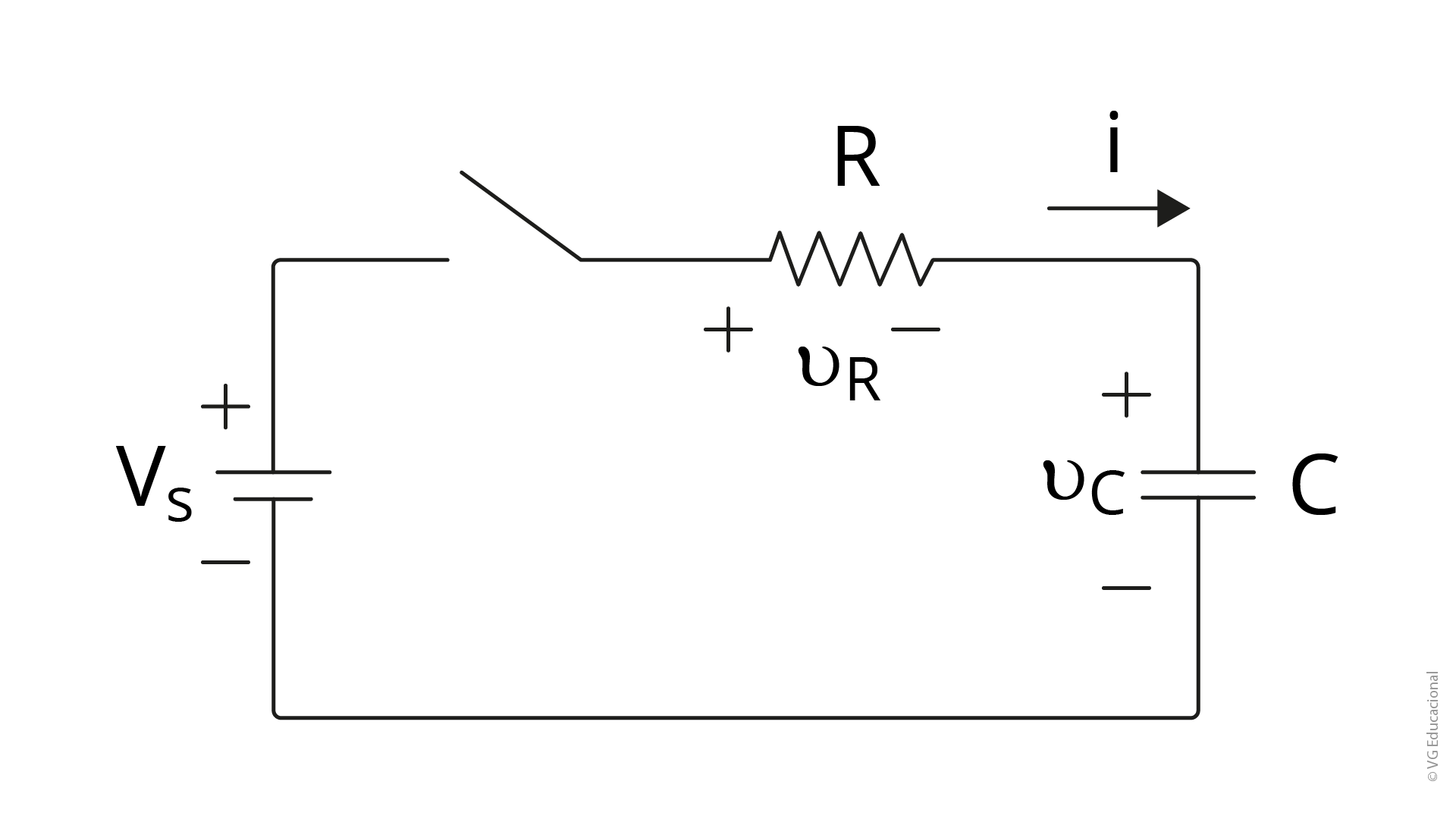
Dado um circuito RC, conforme o da figura apresentada, e considerando R=500Ω, C = 10μF e \({{V}_{s}}\) = 15V, calcule o período transitório do circuito, ou seja, o valor da constante de tempo necessário para que o mesmo esteja completamente descarregado (5τ), e assinale a alternativa correta.

Ano: 1999
Comentário: Este filme expressa o nascimento das empresas Microsoft e Apple, trazendo toda a revolução tecnologia que essas empresas trouxeram ao mundo, interligando todas as pessoas por meio da tecnologia, na qual a base são circuitos elétricos.
Para conhecer mais sobre o filme, acesse o trailer a seguir.

Editora: AMGH
Autor: Matthew N. O. Sadiku
ISBN: 8580553024
Comentário: Este livro traz, de maneira didática e com aplicações das teorias de circuitos elétricos, uma abordagem prática e profunda sobre análises de circuitos de primeira ordem e suas aplicações.
Aprendemos a fazer análise de circuitos elétricos com armazenamentos de energia, sendo eles capacitores ou indutores.
Fazendo a análise desses circuitos, vimos como os mesmos se comportam para armazenar (carregar) e descarregar a carga elétrica, conseguindo chegar a equações que descrevem o comportamento das grandezas medidas em um circuito, sendo estas tensão, corrente, potência e energia, com entradas em corrente contínua (cc).
Vimos que o comportamento da tensão e corrente e os dispositivos de armazenamento de energia, indutores e capacitores se comportam de maneira análoga; logo, ao se compreender o processo de um, conseguimos fazer uma análise rápida para o outro.
ALEXANDER, C. K.; SADIKU, M. N. O. Fundamentos de circuitos elétricos . 5. ed. São Paulo: Editora Bookman, 2013.
NILSSON, J. W.; RIEDEL, S. A. Circuitos elétricos . 8. ed. São Paulo: Pearson Prentice Hall, 2009.
SADIKU, M. N. O.; MUSA S. M.; ALEXANDER C. K. Análise de circuitos elétricos com aplicações . 5. ed. São Paulo: Editora AMGH Editora, 2014.