A fim de iniciarmos nossos estudos em circuito de 2ª ordem, iniciaremos pela análise de circuito de \(RLC\) em série, conforme a Figura 4.1, o qual contém um resistor \(R\), indutor \(L\) e um capacitor \(C\).

O circuito apresentado é excitado pela energia inicialmente armazenada nos armazenadores de energia, sendo esses elementos o indutor e o capacitor, sendo representada pela tensão inicial \(V_0\) no capacitor e pela corrente inicial \(I_0\) no indutor.

Aplicando a \(LKT\) no circuito, fazendo a análise matemática, a fim de simplificar e organizar a equação resultante, temos a seguinte equação:

\(\frac{{{d}^{2~}}i}{d{{t}^{2}}}+\frac{R}{L}\frac{di}{dt}+\frac{i}{LC}=0\) (4.1)

Sendo esta a equação diferencial de segunda ordem, é o motivo para os circuitos \(RLC\) serem chamados de circuitos de segunda ordem. A fim de resolvermos esta equação, é necessário termos duas condições iniciais: o valor de \(i\) e sua primeira derivada ou os valores iniciais de alguma \(i\) e \(v\).

A fim de solucionar a Equação 4.1, vamos utilizar a forma exponencial.

\(i=A{{e}^{st}}\) (4.2)

Substituindo em 4.1

\(A{{s}^{2~}}{{e}^{st}}+\frac{AR}{L}s{{e}^{st}}+\frac{A}{LC}{{e}^{st}}=0\) (4.3)

em que \(A\) e \(s\) são constantes a serem determinadas, assim, podemos simplificar e procurar somente a seguinte expressão:

\({{s}^{2}}+\frac{R}{L}s+\frac{1}{LC}=0\) (4.4)

Para Sadiku, Musa e Alexander  (2014, p. 283), “A equação quadrática é conhecida como equação característica da equação diferencial”, sendo esta a Equação 4.1, uma vez que as raízes da equação ditam as características básicas de \(i\). As duas raízes são definidas de forma condensada como:

\({{s}_{1}}=\alpha +\sqrt{{{\alpha }^{2}}-{{\omega }_{0}}^{2}}\)  (4.5)

\({{s}_{2}}=\alpha -\sqrt{{{\alpha }^{2}}-{{\omega }_{0}}^{2}}\) (4.6)

Em que:

\(\alpha =\frac{R}{2L}\) (4.7)

\({{\omega }_{0}}=\frac{1}{\sqrt{LC}}\) (4.8)

As raízes \(s_1\) e \(s_2\) naturais são chamadas de frequências naturais, medidas em nepers por segundo (Np/s), pois estão associadas à resposta natural do circuito; \(ω_0\) é conhecido como frequência ressonante ou frequência natural não amortecida expressa em radianos por segundo (rad/s); e \(_α\) é a frequência de neper ou fator de amortecimento expresso em nepers por segundo. Reescrevendo a Equação 4.4 em função de \(_α\) e \(ω_0\), temos:

\({{s}^{2}}+2\alpha s+{{\omega }_{0}}^{2}=0\) (4.9)

Sendo a Equação 4.1 uma equação linear, a combinação das soluções acima gera a solução completa desta, logo a resposta natural de um circuito \(RLC\) em série é:

\(i\left( t \right)={{A}_{1}}{{e}^{{{s}_{1}}t}}+{{A}_{2}}{{e}_{{}}}^{{{s}_{2}}t}\) (4.10)

Em que \(A_1\) e \(A_2\) são determinadas a partir dos valores iniciais de i(0) e di(0)/dt.

Dada as soluções \(s_1\) e \(s_2\), temos três tipos de soluções:

1. Se \(α > ω0\), temos o caso de amortecimento supercrítico;
2. Se \(α = ω0\), temos o caso de amortecimento crítico;
3. Se \(α < ω0\), temos o caso de subamortecimento.

Agora, podemos fazer a análise da resposta a um degrau de um circuito \(RLC\) em série.

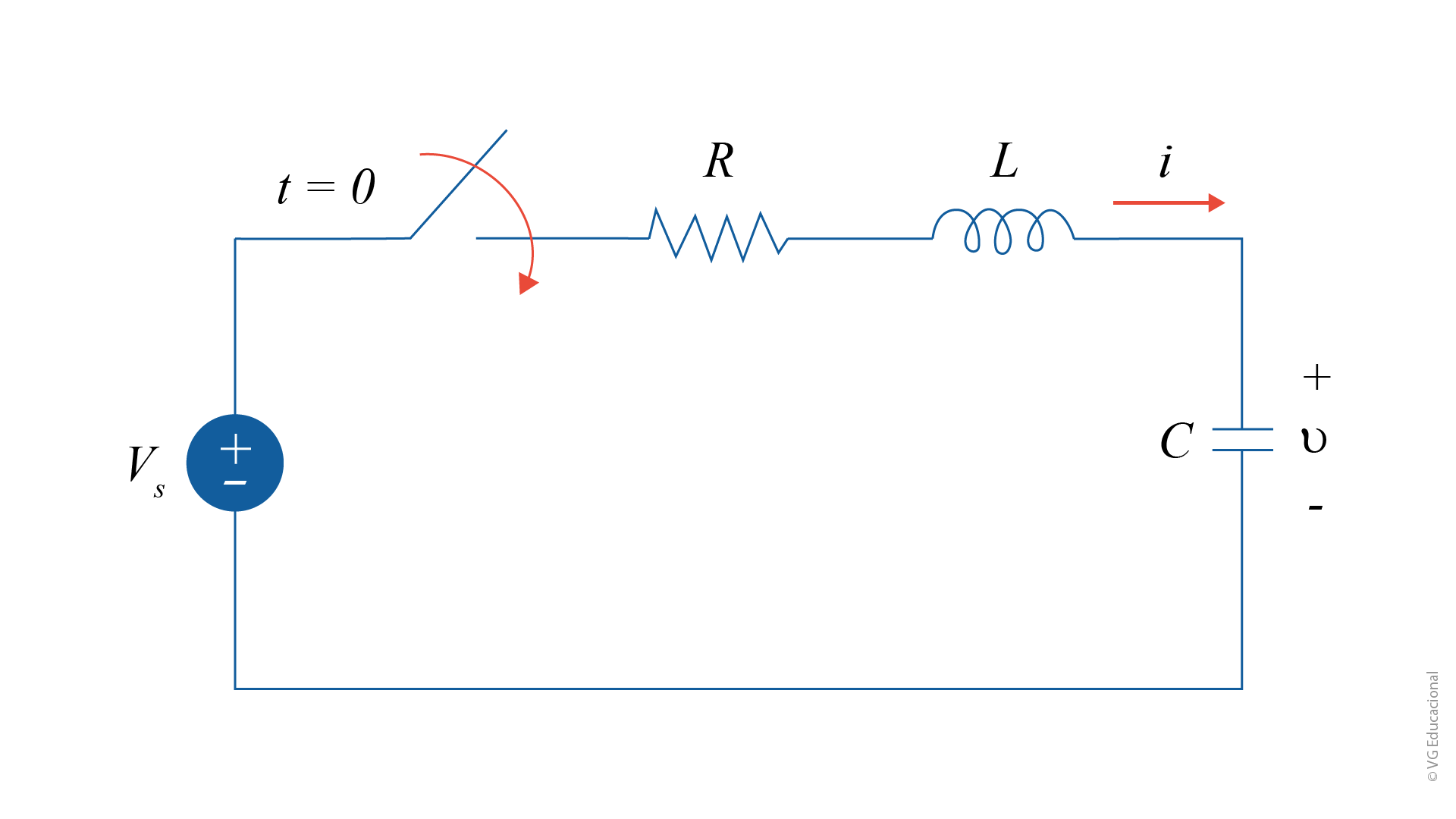
Tendo como base a Figura 4.2, aplicamos a \(LKT\) no circuito para \(t > 0\). Fazendo as simplificações matemáticas, temos:

\(\frac{{{d}^{2~}}v}{d{{t}^{2}}}+\frac{R}{L}\frac{dv}{dt}+\frac{v}{LC}=\frac{{{V}_{s~}}}{LC}\) (4.11)

Ela tem a mesma forma da Equação 4.1. Os coeficientes são os mesmos, no entanto a variável é diferente. Logo, a equação característica para o circuito \(RLC\) em série não é afetada pela presença da fonte \(CC\).

Logo, a resposta da Equação 4.11 tem duas componentes: a resposta (ou componente) transitória \(v_t(t)\) e resposta de estado estável \(v_{ss}(t)\):

\(v\left( t \right)={{v}_{t}}\left( t \right)+{{v}_{ss}}\left( t \right)\) (4.12)

Sabendo que a resposta transiente \(v_t(t)\) é a componente da resposta total que se exige com o tempo, a solução é obtida conforme a Equação 4.10. A resposta de estado estável é o valor final de \(v(t)\). Para o circuito da Figura 4.2, o valor final, então, é o mesmo da fonte \(v_s\).

A solução completa para os casos é descrita conforme:

\(v\left( t \right)={{V}_{s}}+{{A}_{1}}{{e}^{{{s}_{1}}t}}+{{A}_{2}}{{e}^{{{s}_{2}}t}}\) (Amortecimento supercrítico) (4.13)

\(v\left( t \right)={{V}_{s}}+\left( {{A}_{1}}+{{A}_{2}}t \right){{e}^{-\alpha t}}\) (Amortecimento crítico) (4.14)

\(v\left( t \right)={{V}_{s}}+({{A}_{1}}cos\left( {{\omega }_{d}}t \right)+{{A}_{2}}sen\left( {{\omega }_{d}}t \right)){{e}^{-\alpha t}}\) (Subamortecimento) (4.15)

Sendo \(A_1\) e \(A_2\) constantes obtidas das condições iniciais: \(v(0)\) e \(dv(0)/dt\).

Dessa maneira, finalizamos a obtenção da resposta de um circuito \(RLC\) em série a um degrau de tensão. Um circuito \(RLC\) em série é muito utilizado em sistemas de rádio e telecomunicações e também em sistemas de instrumentação. A característica de amortecimento e frequência de oscilação permite que o mesmo seja utilizado como um filtro de corrente, bloqueando uma determinada faixa de frequência e permitindo a passagem de outra faixa de frequência.

Sadiku, Musa e Alexander (2014) afirmam que circuitos ressonantes, sejam em série e ou em paralelo são comumente usados em receptores de TV e rádio, para separar sinais de áudio da onda portadora de radiofrequência, por exemplo.

Circuitos \(RLC\) em paralelo tem diversas aplicações, como em projetos de filtros e redes de comunicações.

A Figura 4.3 mostra um circuito \(RLC\) em paralelo, em que a resistência \(R\), o indutor \(L\) e o capacitor \(C\) estão associados em paralelo; todos os componentes têm a mesma diferença de potencial em seus nós.

Aplicando a \(LKC\) ao nó superior e fazendo a análise matemática, a fim de simplificar a equação resultante, chegamos à seguinte expressão:

\(\frac{{{d}^{2~}}v}{d{{t}^{2}}}+\frac{1}{RC}\frac{dv}{dt}+\frac{v}{LC}=0\) (4.16)

Logo, fazendo as simplificações conforme usada a análise dos circuitos \(RLC\) em série, chegamos à seguinte simplificação:

\({{s}^{2}}+\frac{1}{RC}s+\frac{1}{LC}=0\) (4.17)

As raízes dessa equação podem ser expressas pelas seguintes equações:

\({{s}_{1}}=\alpha +\sqrt{{{\alpha }^{2}}-{{\omega }_{0}}^{2}}\)  (4.18)

\({{s}_{2}}=\alpha -\sqrt{{{\alpha }^{2}}-{{\omega }_{0}}^{2}}\) (4.19)

em que:

\(\alpha =\frac{1}{2RC}\) (4.20)

\({{\omega }_{0}}=\frac{1}{\sqrt{LC}}\) (4.21)

Os nomes desses termos permanecem conforme já mencionado anteriormente. Repetindo a solução da equação de segundo grau, temos três soluções possíveis dependendo das relações de \(_α\) e \(ω_0\).

A fim de obtermos a resposta de um circuito \(RLC\) em paralelo a um degrau, tomaremos como base a Figura 4.4.

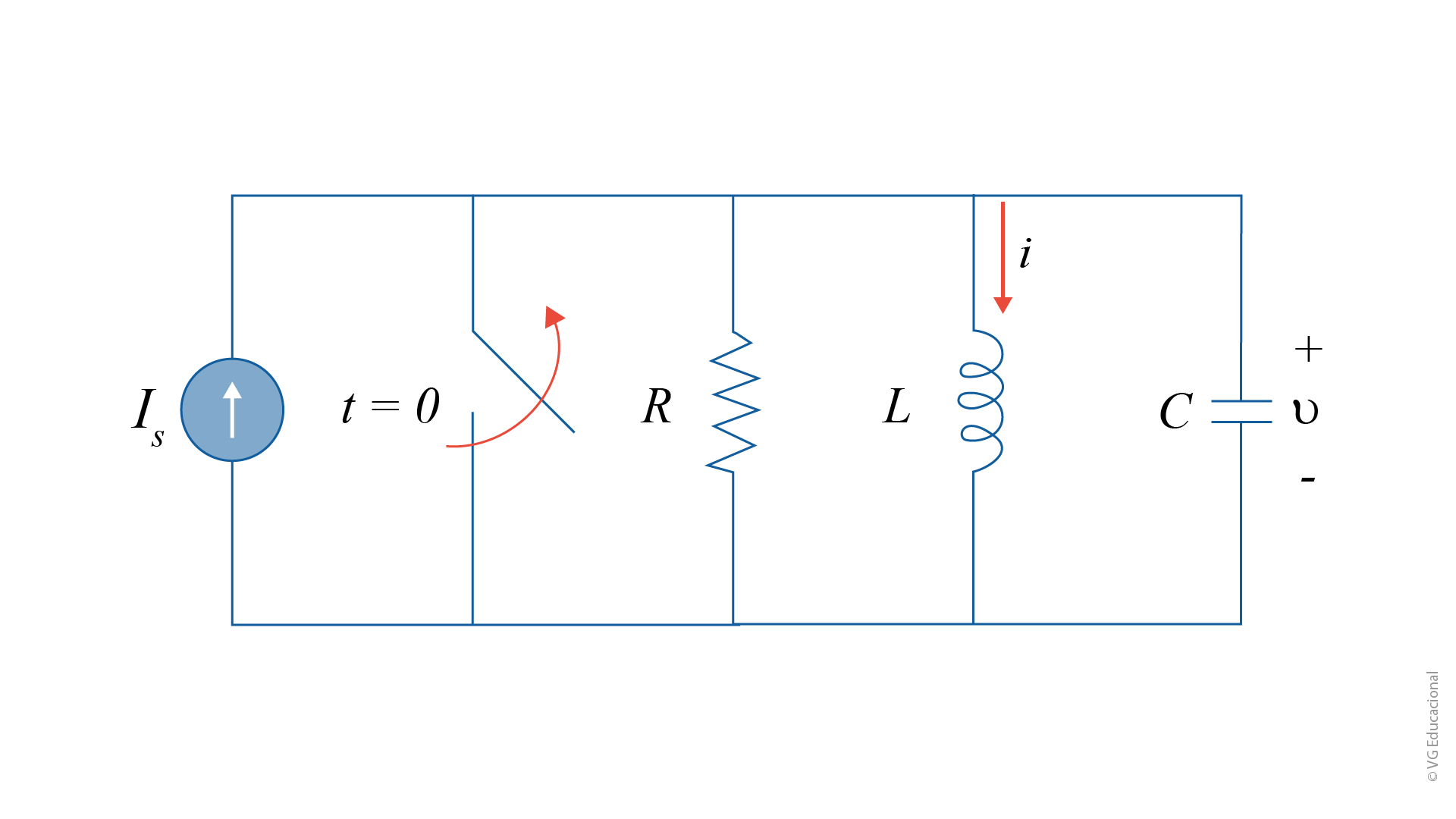
Queremos determinar \(_i\), resultante da aplicação súbita de uma corrente \(CC\). Aplicando a \(LKC\) ao nó superior para \(t > 0\) e fazendo as análises e simplificações matemáticas, chegamos à seguinte equação:

\(\frac{{{d}^{2~}}i}{d{{t}^{2}}}+\frac{1}{RC}\frac{di}{dt}+\frac{i}{LC}=\frac{{{I}_{S}}}{LC}\) (4.16)

A solução a essa equação consiste na soma da resposta transiente \(i_t(t)\) e da resposta de estado estável \(I_{ss}(t)\).

\(i\left( t \right)={{i}_{t}}\left( t \right)+{{i}_{ss}}\left( t \right)\) (4.23)

Sabendo que a resposta transiente \(i_t(t)\) é a componente da resposta total que se exige com o tempo, a resposta de estado estável é o valor final de \(i_t(t)\). Para o circuito da Figura 4.4, o valor final é o mesmo da fonte \(i_{ss}\).

A solução completa para os casos é descrita conforme:

\(i\left( t \right)={{I}_{s}}+{{A}_{1}}{{e}^{{{s}_{1}}t}}+{{A}_{2}}{{e}^{{{s}_{2}}t}}\) (Amortecimento supercrítico) (4.13)

\(i\left( t \right)={{I}_{s}}+\left( {{A}_{1}}+{{A}_{2}}t \right){{e}^{-\alpha t}}\) (Amortecimento crítico) (4.14)

\(i\left( t \right)={{I}_{s}}+({{A}_{1}}cos\left( {{\omega }_{d}}t \right)+{{A}_{2}}sen\left( {{\omega }_{d}}t \right)){{e}^{-\alpha t}}\) (Subamortecimento) (4.15)

Sendo \(A_1\) e \(A_2\) constantes obtidas das condições iniciais: \(i(0)\) e \(di(0)/dt\).

Dessa maneira, finalizamos a obtenção da resposta de um circuito \(RLC\) em paralelo a um degrau de tensão. O circuito \(RLC\) paralelo é muito encontrado (como o circuito \(RLC\) série) em sistemas de telecomunicações. Nos rádios antigos, era utilizado um arranjo \(RLC\) paralelo para efetuar a sintonia da rádio desejada, por meio de um capacitor variável (para mudar as frequências do circuito).

Posteriormente, tais capacitores variáveis foram substituídos por varicaps (que são diodos que possuem capacitância variável) e, por fim, no rádio digital, é comum que o processo de sintonia seja feito exclusivamente via software (rádios que apresentam esse sistema são chamados de SDR - Software Defined Radio ou Rádio definido por Software (tradução livre).

Para Sadiku, Musa e Alexander (2014), existem quatro etapas para determinarmos as respostas a um degrau \(x(t)\), dado um circuito de segunda ordem, sendo esse método aplicado a circuitos \(RLC\) em série ou em paralelo, com uma ou mais fontes independentes com valores constantes. Seguem os quatros passos para análise.

1. Primeiramente, determinamos as condições iniciais \(x (0)\) e \(dx (0) /dt\) e o valor final \(x (∞)\).
2. Desativamos as fontes independentes e encontramos a forma da resposta transiente \(x_t(t)\), aplicando \(LKC\) e \(LKT\). Assim que for obtida uma equação diferencial de segunda ordem, determinamos suas raízes características. Dependendo se a resposta for com amortecimento supercrítico, com amortecimento crítico ou subamortecimento, obtemos \(x_t(t)\) com duas constantes conhecidas, como fizemos anteriormente.
3. Obtemos a resposta de estado estável como \(X_{ss}(t)\) = \(X (∞)\), em que o segundo termo é o valor final de \(x\), obtido na etapa 1.
4. A resposta total agora é encontrada com a soma das respostas transientes e de estado estável. Estabelecemos as constantes associadas com a resposta transiente impondo as condições iniciais \(x(0)\) e \(dx(0)/dt\), determinadas no item 1.
   

Dessa maneira, conseguimos encontrar a resposta a um degrau de um circuito de segunda ordem, inclusive aqueles com amplificadores operacionais.

Até o presente momento, temos limitado nossos estudos a circuito de corrente contínua. Agora iniciaremos os conceitos de circuitos nos quais a tensão ou a corrente variam com o tempo. Abordaremos conceitos de circuitos com corrente alternada, cálculos de potencias e circuitos \(RLC\) em corrente alternada de maneira rápida. Por meio do cálculo de potências de um circuito \(RLC\), podemos modelar o efeito observado nas linhas de transmissão de energia, em que parte da energia transmitida é perdida em forma de campo elétrico e magnético.

Circuito de Corrente Alternada

Estudaremos particularmente a excitação senoidal com variação no tempo ou simplesmente senoide.

Sadiku,  Musa e Alexander (2014) definem uma senoide com um sinal que possui a forma da função cosseno ou seno. Dessa maneira, uma corrente senoidal é conhecida como corrente alternada (\(CA\)).

Consideremos a tensão senoidal:

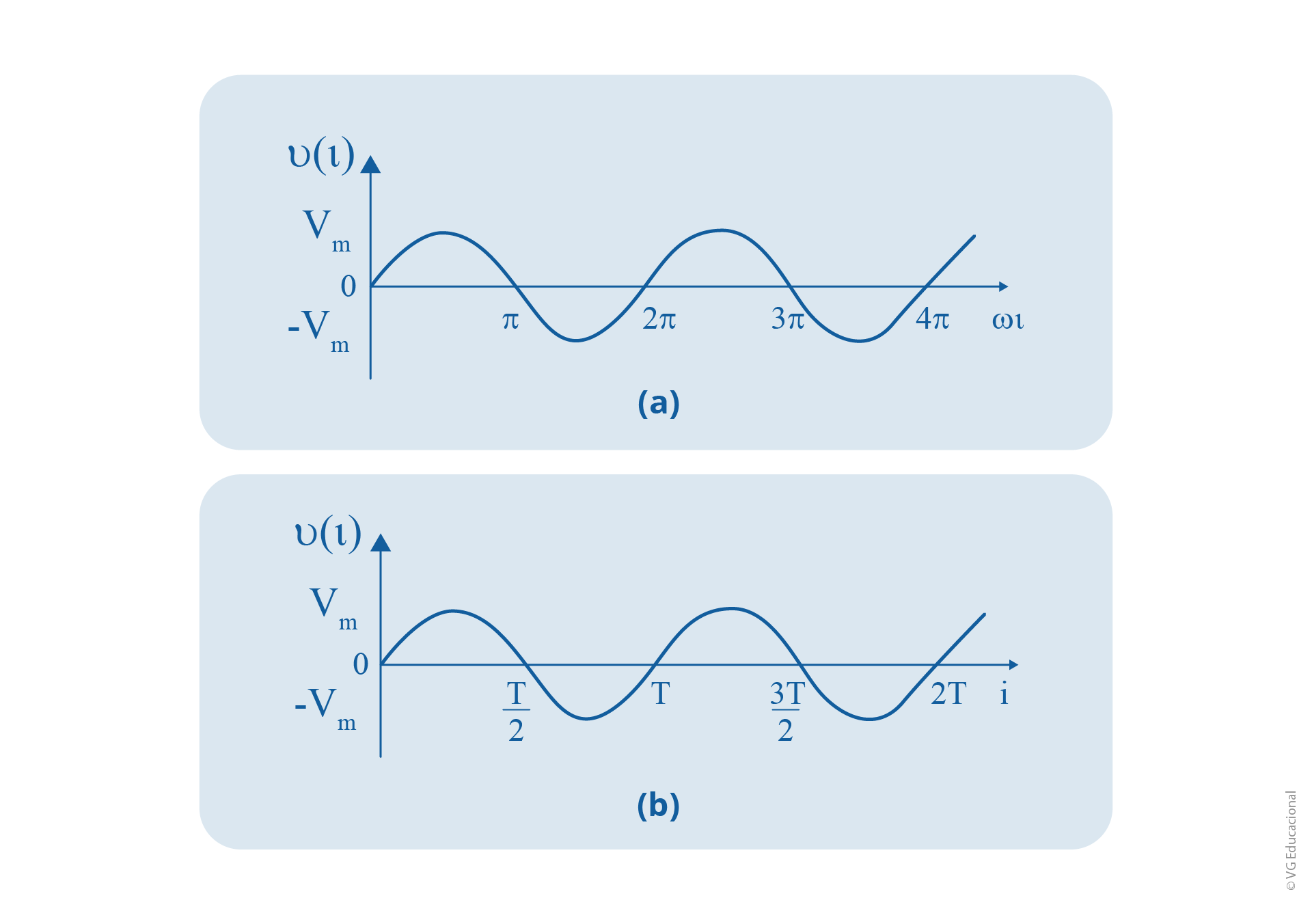
\(v\left( t \right)={{V}_{m}}sen\left( \omega t \right)\) (4.27)

em que \(V\) é a amplitude da senoide, \(ω\) é a frequência angular em radianos/s e \(ωt\) é o argumento da senoide.

Tendo um sinal senoidal, ela se repete em períodos; representaremos esse período da senoide pela letra \(T\), em que seu valor é equivalente a 2\(\pi \)\(/ω\). O inverso desse valor é conhecido com frequência cíclica, representado pela letra \(f\), sendo equivalente a \(T^{-1}\) e dada em hertz (Hz).

Sadiku,  Musa e Alexander (2014) afirmam que senoides são expressas de maneira simples em termos de fasores, que são mais convenientes de serem trabalhados que as funções seno e cosseno, sendo que um fasor é definido pelo mesmo com um número complexo que representa a amplitude e a fase de uma senoide.

Não é nosso objetivo entrar em todas as propriedades de um fasor, como também fazer operações com o mesmo, mas, sim, apresentar como as técnicas já trabalhadas, associadas a técnicas que serão trabalhadas posteriormente, permitem a análise de circuitos sujeitos a corrente contínua e alternada.

Para se realizar análises de circuitos com correntes alternadas, podemos utilizar a lei de ohm, leis de Kirchhoff e outros métodos já descritos em outras unidades, aplicando conforme a necessidade, visto que essas leis são válidas para circuitos \(CA\).

Segundo Sadiku,  Musa e Alexander (2014), a análise de circuitos \(CA\) normalmente requer três etapas:

1. transformar o circuito para o domínio de fasores ou da frequência;
2. solucionar o problema usando técnicas de circuitos;
3. transformar o fasor resultante para o domínio do tempo.

Logo, os métodos e as leis já estudados podem ser usados para nossas futuras análises. Circuitos de corrente alternada estão presentes em toda a rede elétrica de distribuição, na grande maioria das indústrias e nos grandes sistemas elétricos de potência.

Cálculos de Potência

A potência é o valor mais importante em sistemas de energia elétrica, eletrônicos e de comunicação, pois envolve a transmissão de energia de um ponto para outro.

Estudaremos a potência instantânea e a potência média de um sistema.

Para Sadiku,  Musa e Alexander (2014), a potência instantânea é a potência em qualquer instante, medida em watts, logo, ela é a taxa na qual um elemento absorve energia. Esta é dada pela seguinte equação:

\(p\left( t \right)=v\left( t \right)i\left( t \right)\) (4.28)

sendo a tensão \(v(t)\) e a corrente \(i(t)\) elementos que variam com o tempo, a potência instantânea também apresenta esse comportamento, portanto, é difícil de ser medida.

A potência média é a média da potência ao longo de um período, medida em watts, logo, fazendo a análise matemática do mesmo, em um período. Tendo os componentes em \(CA\), chegaremos à seguinte equação:

\(P=\frac{1}{2}Re\left[ VI* \right]=\frac{1}{2}{{V}_{m}}{{I}_{m}}cos\left( {{\theta }_{v}}-{{\theta }_{i}} \right)\) (4.29)

Em que \({{\theta }_{v}}\) e \({{\theta }_{i}}\) são os ângulos de defasagem da tensão e corrente, respectivamente.

Sabendo que essa equação implica em um circuito puramente resistivo, pois esse tipo de carga sempre absorve potência, enquanto uma carga reativa (\(L\) ou \(C\)) não absorve nenhuma potência média.