Controle de Sistemas
Visão Geral de um Sistema de Controle e Resposta Transitória de Sistemas Dinâmicos
Tempo de leitura do conteúdo estimado em 1h20min.
Olá, estudante! Tudo bem?
Iniciamos nossa jornada para entender como funcionam os sistemas de controle. Para isso, você verá mais detalhes, numa visão geral, desses tipos de sistemas, elementos que, frequentemente, estão presentes, como esses sistemas são representados gráfica e matematicamente e aprenderá a analisar o comportamento dos sistemas reais na prática. Dessa forma, neste seu contato com os sistemas de controle, você entenderá quais equipamentos são utilizados e terá uma visão geral de como representar os sistemas reais, seja para o desenvolvimento do sistema de controle ou mesmo para estudar o comportamento dos sistemas na prática. Além disso, focaremos nossos esforços acerca do entendimento do comportamento dinâmico, o que definimos como resposta transitória, até que o sistema se estabilize em seu comportamento ao longo do tempo. Vamos lá?
Muito se fala sobre os avanços da Indústria 4.0, e, com certeza, você já se deparou com esse termo, certo? Você sabia que uma das estratégias para colocar em prática as premissas dessa nova forma é o desenvolvimento de sistemas automatizados, que permitem o controle dos processos industriais desenvolvidos na indústria ou parte desses? Entender como controlar um sistema na prática faz parte, inclusive, de estratégias capazes de promover avanços tecnológicos à indústria, maior competitividade frente a concorrentes, maior sustentabilidade e, até mesmo, vários tipos de economias, de gastos em energia elétrica, por exemplo.
Começaremos nosso estudo reconhecendo os principais elementos de um sistema de controle, considerando ainda a evolução tecnológica ao longo da história e entendendo algumas das principais aplicações e configurações básicas.
Visão Geral
Entende-se como sistema de controle um conjunto de interconexão de componentes em busca de se obter uma resposta desejada. Também é denominado sistema um conjunto de partes conectadas e/ou relacionadas para formação de um todo, podendo ser físico, econômico etc. Para análise, utilizamos fundamentos da Teoria de Sistemas Lineares, por exemplo, caso seja possível considerar o comportamento desse sistema como linear (que satisfaz as propriedades de superposição e homogeneidade) ou linearizável. Aliás, um sistema que apresenta comportamento linear possui resposta ao longo do tempo representada por uma função linear, e outra questão importante a ser salientada é que o sistema de controle fará o controle de um dado componente ou processo, industrial ou não.
Os sistemas de controle são uma parte integrante da sociedade moderna. Inúmeras aplicações estão à nossa volta: os foguetes são acionados, e o ônibus espacial decola para orbitar a Terra; envolta em jatos de água de resfriamento, uma peça metálica é usinada automaticamente; um veículo autônomo distribuindo materiais para estações de trabalho em uma oficina de montagem aeroespacial desliza ao longo do piso buscando seu destino. [...] No interior de nossos próprios corpos existem inúmeros sistemas de controle, como o pâncreas, que regula o nosso nível de açúcar no sangue (NISE, 2017, p. 28).
Além disso, observe que um sistema de controle poderá ser formado por outros sistemas menores (ou mais simples), definidos como subsistemas, e mais de um processo (ou planta). Na saída, espera-se obter uma resposta desejada, com também um dado desempenho esperado, considerando uma entrada especificada. Geralmente, inclusive, nos referimos ao controle de uma planta industrial. Veja, na imagem adiante, a representação geral de um sistema de controle.
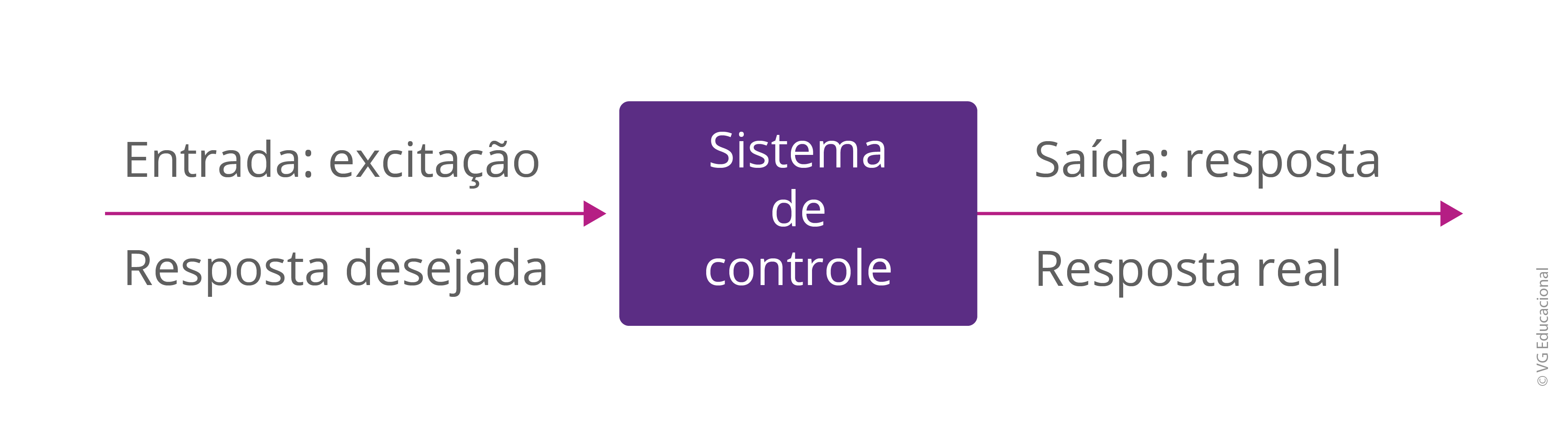
Fonte: Nise (2017, p. 28).
#PraCegoVer: diagrama com uma seta apontando da esquerda para a direita com o texto “Entrada; excitação, Resposta desejada”, seguido por um bloco com o texto “Sistema de Controle” e, por fim, uma seta apontando da esquerda para a direita com o texto “Saída; resposta, Resposta real”.
Como você pode imaginar, dadas essas premissas práticas, fica relativamente claro que existem diversas possíveis vantagens, em geral, de se utilizar um (ou mais) sistema(s) de controle. Dentre elas, é possível elencar: possibilidade de amplificar a potência do sistema real ao qual o controle estará associado; realização do controle de maneira remota (especialmente considerando os avanços tecnológicos ao longo dos anos); estabelecimento de uma entrada numa dada forma mais conveniente; atendimento a questões como a possibilidade de compensar possíveis perturbações a que o sistema pode estar sujeito.
Por fim, neste subtópico, podemos ressaltar pontos históricos gerais importantes capazes de auxiliar você, estudante, acerca do porquê utilizamos certos tipos de estratégias de controle, em específico, além de alguns equipamentos frequentemente utilizados. Nesse sentido, é importante salientar que sistemas de controle com retroação (também mais conhecidos como sistemas de controle com realimentação), os quais veremos em mais detalhes a partir do próximo tópico, possuem a primeira utilização datada de 300 anos antes da era cristã. Esses tipos de sistemas, onde há a possibilidade de associação da saída junto à entrada, basicamente, na ocasião, foram desenvolvidos com o objetivo de regular mecanismos de uma boia para controle de nível de líquidos. Além disso, a forma de controle mais próxima do que utilizamos, nos dias atuais, advém do que se conhece como o primeiro controlador automático com realimentação, utilizado num processo industrial, mais conhecido como regulador de esferas (veja a imagem adiante), desenvolvido por James Watt para controlar máquinas a vapor, de funcionamento totalmente mecânico.
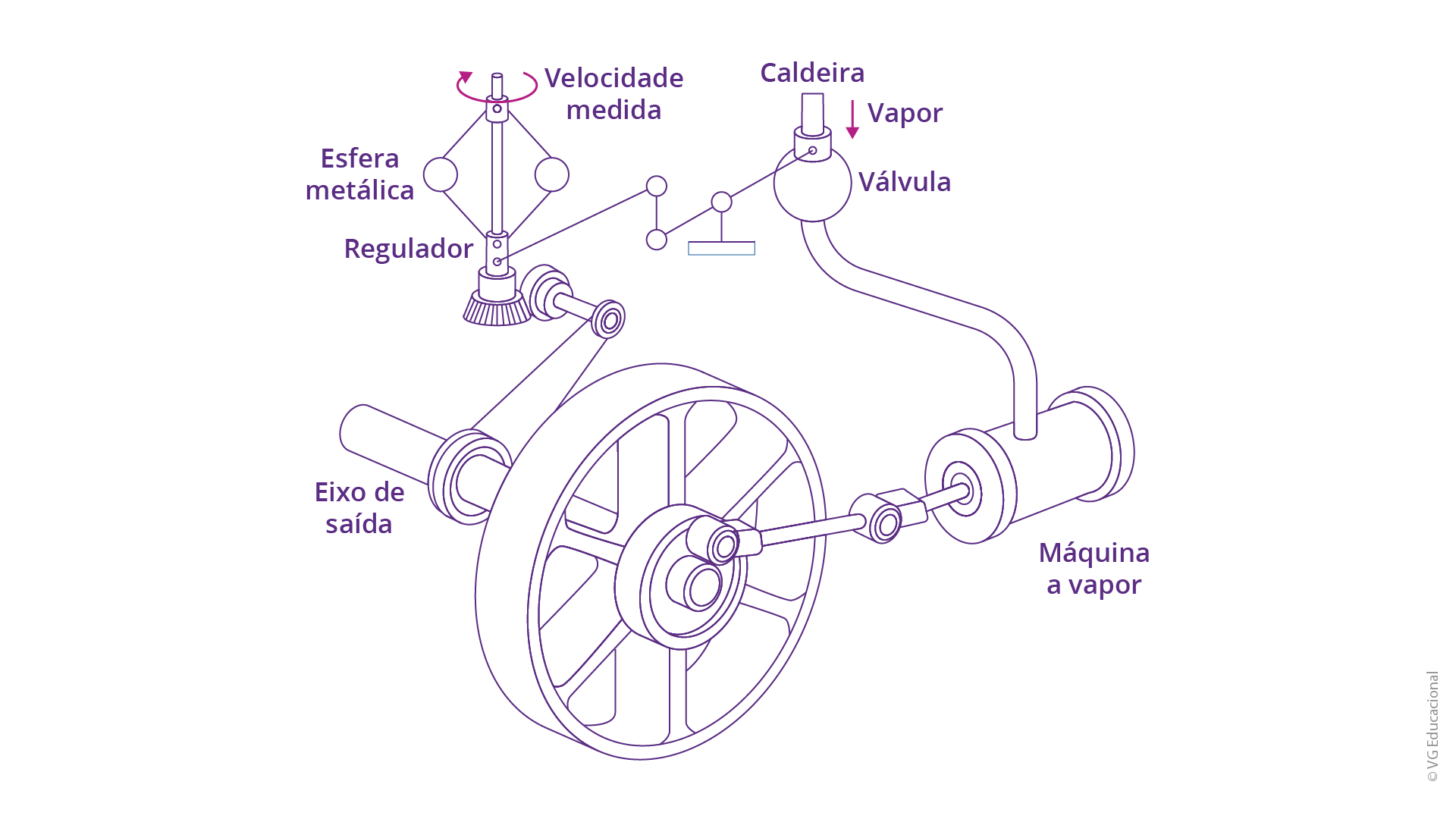
Fonte: Dorf (2018, p. 23).
#PraCegoVer: roda associada a uma máquina a vapor, que está conectada a uma caldeira que envia vapor por meio de uma válvula. Essa caldeira está diretamente ligada a um mecanismo regulador, com esferas metálicas e um ponto de medição de velocidade, associado ao eixo de saída da roda.
Além disso, assim como muitas outras tecnologias, boa parte da evolução tecnológica dos sistemas de controle está associada ao cenário de guerras, especialmente da Segunda Guerra Mundial, por estratégias como o desenvolvimento de pilotos automáticos para aviões. Em seguida, tem-se o desenvolvimento de teorias acerca da estabilidade dos sistemas na prática, estratégias de otimização aplicadas diretamente aos sistemas de controle, incorporação do comando numérico, robotização, desenvolvimento de estratégias definidas como controle robusto, incorporando necessidades a serem aplicadas por conta de variações vistas devido a perturbações constantes, até chegarmos aos sistemas de automação, com a incorporação de elementos como a interface homem/máquina, dentre outras possibilidades.
Uso atual de sistemas de controle — visão geral
Atualmente, sistemas de controle são utilizados ainda em estratégias como orientação, navegação e controle de mísseis e para uso em veículos espaciais, aviões e navios. Além disso, existem sistemas de controle aplicados em sistemas de automação residencial, e, cada vez mais, cresce mais a possibilidade de uso fora da realidade industrial.
A seguir, apresento-lhe mais detalhes de um sistema de controle em dois sistemas práticos: um sistema de controle manual de nível; um sistema de controle de direção de automóvel.
Exemplos Práticos
Como primeiro exemplo prático, suponha que seja necessário, para controle do nível de água num reservatório de um comércio, o desenvolvimento de um sistema de regulação como o apresentado na próxima imagem. A observação do nível é feita por um agente, operador, que consegue ter acesso ao reservatório.
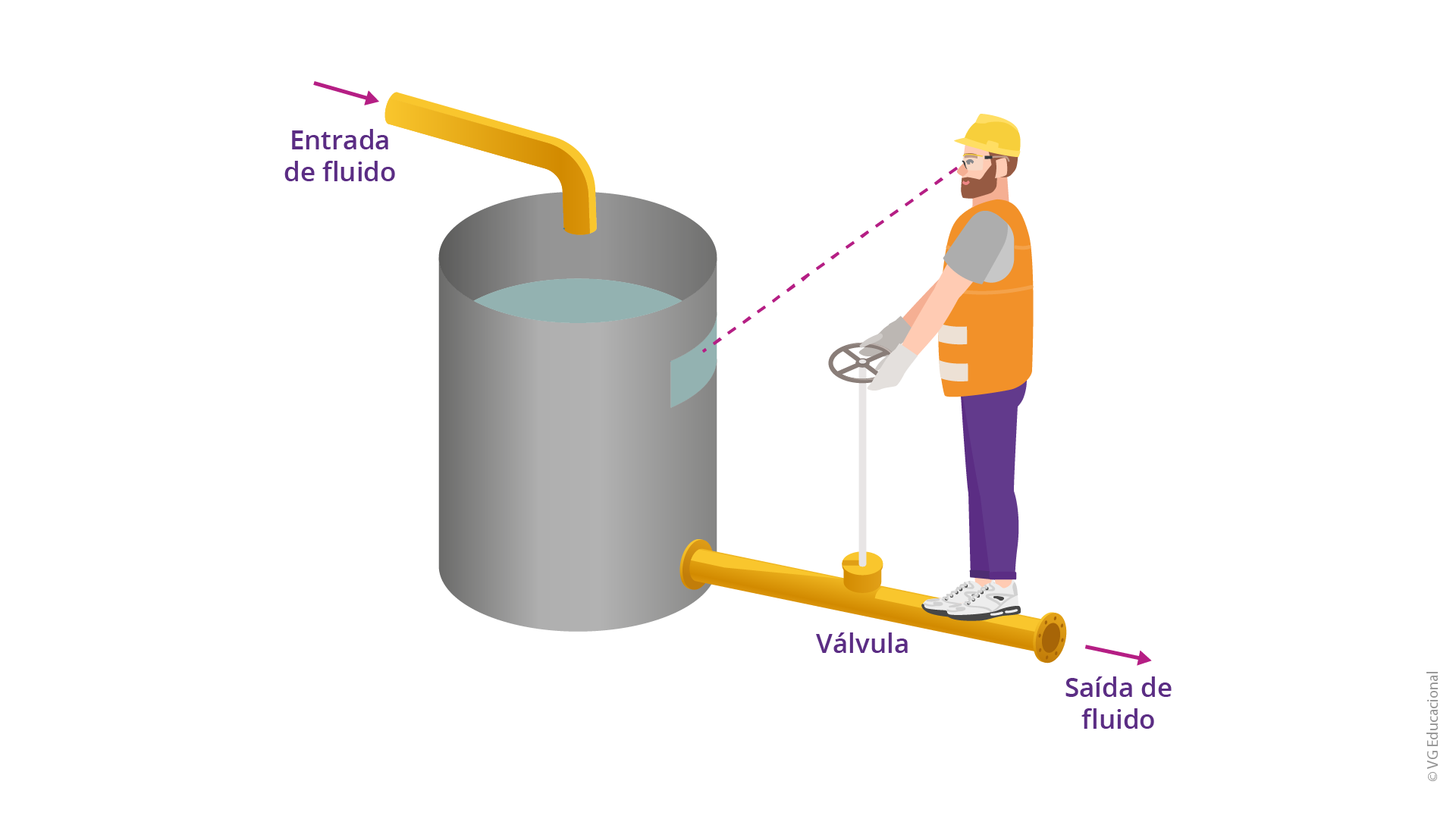
Fonte: Dorf (2018, p. 28).
#PraCegoVer: a figura apresenta a ilustração de um tanque com um cano para a entrada de fluido, e outro cano para a saída deste, associado a uma válvula, controlada por uma pessoa que visualiza o nível desse reservatório.
Observe que a entrada do sistema de controle é o nível de referência do fluido. Nesse caso (ainda em específico da água), o controlador (pessoa responsável por operar o sistema) deve atuar buscando atingi-lo, abrindo e fechando a válvula manual. Além disso, com esse exemplo relativamente simples, perceba que muitos processos que realizamos em nosso dia a dia podem ser partes de um sistema de controle.
Como segundo e último exemplo sobre esse ponto, considere o desenho da situação prática, visto na figura adiante, e o gráfico da resposta da direção de deslocamento ao longo do tempo. Deseja-se obter, para o cenário real, a direção a ser tomada pelo veículo.
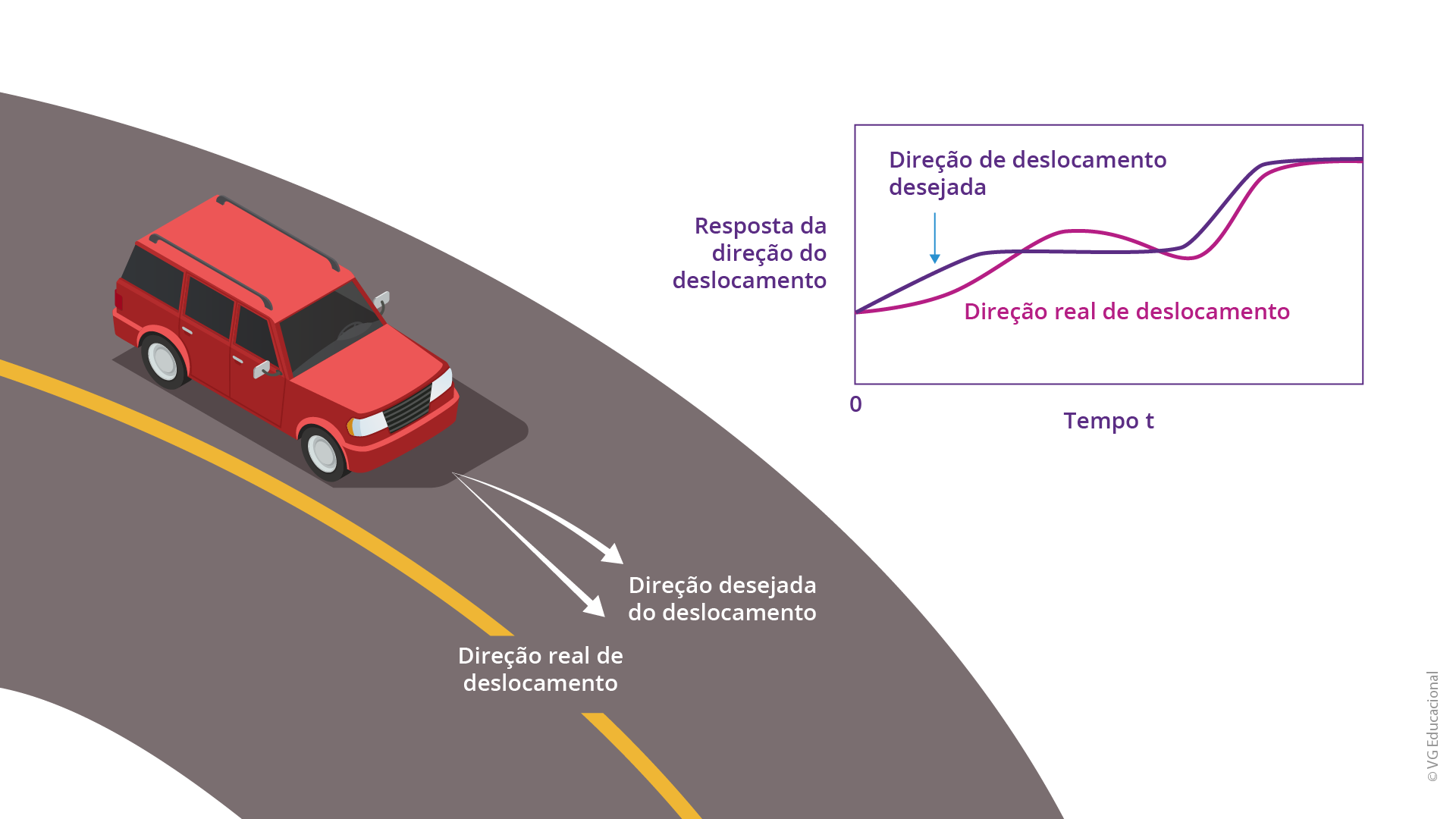
Fonte: Adaptada de Dorf (2018, p. 28).
#PraCegoVer: do lado esquerdo, está a imagem de um veículo trafegando em uma estrada, com a representação de duas trajetórias: a direção real do deslocamento e a direção desejada de deslocamento. Do lado direito, está o gráfico de tempo e resposta da direção de deslocamento, com as curvas do deslocamento desejado e do real, mostrando as variações ao longo do tempo.
Veja também, no exemplo do carro, que um dos objetivos do sistema será promover a segurança por parte do motorista, de forma que o veículo responda de maneira mais rápida possível a comandos estabelecidos pelo motorista.
Os sistemas de controle estão amplamente presentes em processos industriais, dados os avanços tecnológicos e os incentivos e esforços da Indústria 4.0, entretanto, como já visto, existem sistemas de controle que fazem parte de nosso dia a dia, incluindo alguns sistemas de aplicação residencial, por exemplo.
Nesse sentido, é correto afirmar que:
Veja, a seguir, os principais elementos utilizados num sistema de controle e as representações e estratégias de modelagem matemática aplicáveis aos sistemas na prática capazes de auxiliar, inclusive, no projeto dos controladores.
Daremos início à definição dos principais elementos utilizados em sistemas de controle em geral, além de visualizarmos, com isso, uma das principais estratégias utilizadas para fazer também o projeto dos sistemas de controle: a representação dos sistemas na prática (matemática e gráfica). Vamos lá?
Visão Geral
Matematicamente, um sistema pode ser considerado de primeira ordem, segunda ordem ou ordem superior, de acordo com questões como simplicidade, em termos mais especificamente de quantidade de equipamentos, por exemplo, de maneira geral (veremos mais detalhes dessa classificação nos próximos tópicos). Assim, os sistemas dinâmicos, sistemas cujo comportamento varia ao longo do tempo (basicamente, o caso de qualquer sistema na prática), são modelados de acordo com alguns passos gerais (DORF, 2018):
Definição do que é o sistema a ser modelado e qual(is) é(são) seu(s) componente(s).
Formulação do modelo matemático e possíveis hipóteses associadas a seu comportamento.
Escrita da(s) equação(ões) diferencial(is).
Resolução dessa(s) considerando a(s) variável(is) de saída desejável(is).
Exame da(s) solução(ões) obtida(s) junto à(s) hipótese(s) inicialmente levantada(s).
Caso necessário, repetir os passos anteriores para obter uma melhor representação.
- Definição do que é o sistema a ser modelado e qual(is) é(são) seu(s) componente(s).
- Formulação do modelo matemático e possíveis hipóteses associadas a seu comportamento.
- Escrita da(s) equação(ões) diferencial(is).
- Resolução dessa(s) considerando a(s) variável(is) de saída desejável(is).
- Exame da(s) solução(ões) obtida(s) junto à(s) hipótese(s) inicialmente levantada(s).
- Caso necessário, repetir os passos anteriores para obter uma melhor representação.
Geralmente, consideramos como base as variáveis físicas, o que pode ter especificações especiais considerando o tipo de sistema. No caso de sistemas elétricos, por exemplo, temos corrente, carga elétrica, diferença de potencial elétrico (tensão elétrica), resistência elétrica e questões como fluxo e campo magnético. No caso de sistemas mecânicos, de rotação, mais especificamente, temos torque, momento cinético, variação da velocidade angular e do deslocamento angular. No caso de um sistema de translação, força, quantidade de movimento, diferença da velocidade e do deslocamento. Num sistema com fluido, será interessante considerar parâmetros como vazão volumétrica, volume, diferença de pressão e momento dessa. Num sistema térmico, fluxo térmico, energia térmica, fluxo de calor, diferença de temperatura e variações na pressão.
Outras estratégias muito comuns na modelagem matemática envolvem dois tipos principais de representação: a função de transferência e a representação no espaço de estados. A função de transferência de um sistema, capaz de ser representada numa equação diferencial linear invariante no tempo, por exemplo, é definida com base na transformada de Laplace da entrada e da saída desse sistema, com condições iniciais nulas (OGATA, 2010). A seguir, equação diferencial genérica, por exemplo, com y sendo a saída e x sendo a entrada do sistema.
\(a_{0}^{\left( n \right)}y+a_{1}^{\left( n-1 \right)}y+...+a_{n-1}^{{}}y'+{{a}_{n}}y~=\)
\(~b_{0}^{\left( m \right)}x+b_{1}^{\left( m-1 \right)}x+{{b}_{m-1}}x'+{{b}_{m}}x~~~\) (1)
Com n \(\ge \) m, tem-se a função de transferência, G(s):
função de transferência = G(s) = L(saída)/L(entrada) (2)
Ainda:
\(G\left( s \right)~=~\frac{{{b}_{0}}{{s}^{m}}~+~{{b}_{1}}{{s}^{m-1}}+...+{{b}_{m-1}}s+{{b}_{m}}}{{{a}_{0}}{{s}^{n}}+{{a}_{1}}{{s}^{n-1}}+...+{{a}_{n-1}}s+{{a}_{n}}}~~~~~~~\) (3)
Com essa representação, conseguimos representar a dinâmica do sistema de maneira mais simplificada e caracterizar sua ordem de acordo com o polinômio obtido no denominador (OGATA, 2010). Daí surge, efetivamente, a classificação para um sistema de primeira, segunda ou ordem superior.
Já a representação no espaço de estados, amplamente utilizada em estratégias de controle robusto, por exemplo, parte do princípio de o estado de um sistema dinâmico ser o menor conjunto de variáveis (de estado), que pode ser estabelecido para determinar o comportamento do sistema para qualquer instante além do tempo inicial, que pode ser o instante t = 0 s. Além disso, as variáveis de estado não precisam ser necessariamente quantidades físicas mensuráveis ou observáveis, o que é, inclusive, uma possível vantagem de se utilizar tal representação, embora seja mais fácil representar partindo de variáveis passíveis de medição no sistema. O espaço de estados, por sua vez, permite a representação das n variáveis, e a(s) equação(ões) no espaço de estados correlaciona(m) as variáveis de entrada, de saída e de estado (OGATA, 2010). Esses conceitos ficarão mais claros a seguir. Como exemplo, considere um sistema de r entradas e m saídas, relacionadas a n integradores. As entradas são do tipo \({{u}_{1}}\left( t \right),~{{u}_{2}}\left( t \right),~...,~{{u}_{r}}\left( t \right)\); as saídas, \({{y}_{1}}\left( t \right),~{{y}_{2}}\left( t \right),~...,~{{y}_{m}}\left( t \right)\), com as n saídas dos integradores sendo \({{x}_{1}}\left( t \right),~{{x}_{2}}\left( t \right),~...,~{{x}_{n}}\left( t \right)\). Podemos descrever o sistema como:
\(x{{'}_{1}}\left( t \right)~=~{{f}_{1}}\left( {{x}_{1}},~{{x}_{2}},~...,~{{x}_{n}};~{{u}_{1}},~{{u}_{2}},~...,~{{u}_{r}},~t \right)~~~~\) (4)
\(x{{'}_{2}}\left( t \right)~=~{{f}_{2}}\left( {{x}_{1}},~{{x}_{2}},~...,~{{x}_{n}};~{{u}_{1}},~{{u}_{2}},~...,~{{u}_{r}},~t \right)\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\vdots \)
\(x{{'}_{n}}\left( t \right)~=~{{f}_{n}}\left( {{x}_{1}},~{{x}_{2}},~...,~{{x}_{n}};~{{u}_{1}},~{{u}_{2}},~...,~{{u}_{r}},~t \right)\)
As saídas podem ser dadas por:
\({{y}_{1}}\left( t \right)~=~{{g}_{1}}\left( {{x}_{1}},~{{x}_{2}},~...,~{{x}_{n}};~{{u}_{1}},~{{u}_{2}},~...,~{{u}_{r}},~t \right)~~\) (5)
\({{y}_{2}}\left( t \right)~=~{{g}_{2}}\left( {{x}_{1}},~{{x}_{2}},~...,~{{x}_{n}};~{{u}_{1}},~{{u}_{2}},~...,~{{u}_{r}},~t \right)\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\vdots \)
\({{y}_{n}}\left( t \right)~=~{{g}_{m}}\left( {{x}_{1}},~{{x}_{2}},~...,~{{x}_{n}};~{{u}_{1}},~{{u}_{2}},~...,~{{u}_{r}},~t \right)\)
Caso se defina matricialmente, tem-se ainda que:
x’(t) = f(x, u, t) e y(t) = g(x, u, t) (6)
A representação na forma matricial será conveniente especialmente considerando o projeto de controladores robustos. Caso o sistema seja do tipo não linear, podemos fazer a representação na forma linearizada.
SAIBA MAIS
Quer rever como calcular a transformada de Laplace (tanto direta quanto inversa)? Assista à videoaula a seguir, na qual são apresentados os processos feitos, passo a passo, com exemplos práticos, demonstrando como podemos utilizar essa poderosa ferramenta no contexto.
Para saber mais, acesse:
Em termos do sistema de controle mais especificamente, temos os sistemas em malha aberta e/ou fechada, de acordo com a disposição dos elementos de controle e de uma possível ligação existente (ou não) da saída.
Conceitos importantes e tipos de sistemas de controle
#PraCegoVer: o infográfico interativo, intitulado “Conceitos importantes e tipos de sistemas de controle”, apresenta sete botões interativos alinhados verticalmente. À esquerda dos botões, há uma ilustração de um velocímetro com alguns gráficos ao redor. O primeiro botão interativo, intitulado “Perturbação”, ao ser clicado, apresenta o texto “sinal de presença controlada, não controlada ou parcialmente controlada, capaz de afetar de maneira adversa o sistema a ser controlado. Pode ser interno ao sistema ou externo”. O segundo botão interativo, intitulado “Erro”, ao ser clicado, apresenta o texto “diferença matemática entre a saída do sistema controlado e a referência”. O terceiro botão interativo, intitulado “Controlador”, ao ser clicado, apresenta o texto “elemento que desempenha a(s) ação(ões) tomada(s) para obtenção da saída desejável (referência do sistema)”. O quarto botão interativo, intitulado “Variável controlada”, ao ser clicado, apresenta o texto “grandeza ou uma dada condição medida no sistema e controlada por este”. O quinto botão interativo, intitulado “Variável manipulada”, ao ser clicado, apresenta o texto “também conhecida como sinal de controle, é uma grandeza ou uma dada condição no sistema, modificada por parte do controlador, a fim de afetar o valor da variável controlada”. O sexto botão interativo, intitulado “Resposta transitória”, ao ser clicado, apresenta o texto “parcela de transição, até o comportamento permanente do sistema, na resposta dinâmica deste, que pode ocorrer até a ação completa do controlador, ou carregar comportamentos variados, de curta duração, de um sistema não controlado, por exemplo”. O sétimo botão interativo, intitulado “Resposta em regime permanente”, ao ser clicado, apresenta o texto “parcela do comportamento do sistema ao longo do tempo, após a ação completa do controlador, ou ainda durante o período, após possíveis instabilidades da ligação de equipamentos, por exemplo”.
Além disso, é importante observarmos, sobre esse ponto, que existirão basicamente duas estruturas principais de sistemas de controle: o sistema em malha aberta e o sistema em malha fechada. Um sistema em malha aberta, a ser visto na Figura 1.5, é incapaz de realizar compensações, por possuir a associação em série da entrada, controlador e planta, sem interligação com a saída.
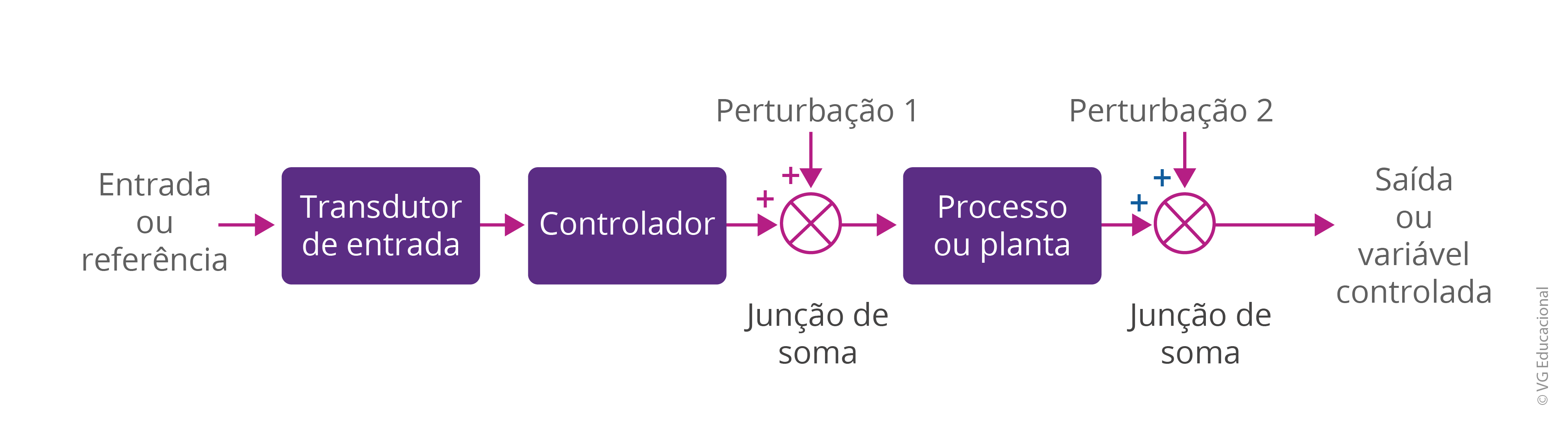
Fonte: Nise (2017, p. 36).
#PraCegoVer: na figura, há um diagrama de blocos com entrada ou referência, seguido por um bloco de transdutor de entrada, por um controlador e por um ponto para adição de perturbação, por meio de uma junção de soma. Em seguida, há o processo ou planta e um segundo ponto de junção de soma, para adição de outra perturbação, até chegar à saída ou à variável controlada.
Já um sistema em malha fechada, visto na Figura 1.6 a seguir, é um tipo de sistema de controle com conexão da saída junto à entrada do controlador (estrutura de realimentação), que permite a compensação de possível(is) perturbação(ões).
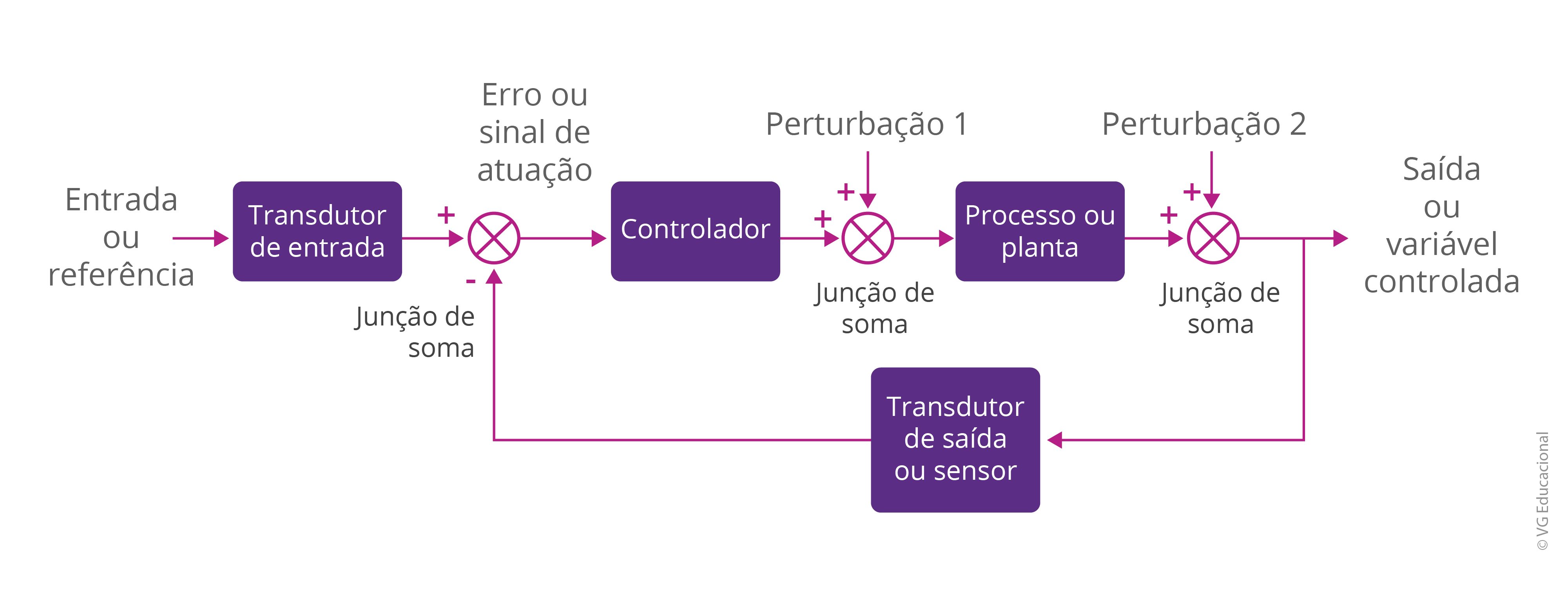
Fonte: Nise (2017, p. 36).
#PraCegoVer: na figura, há um diagrama de blocos com a entrada ou referência, seguida pelo transdutor de entrada, um ponto de junção de soma para seguir para o erro ou sinal de atuação, que está conectado ao bloco controlador. Em seguida, há outra junção de soma com a perturbação 1, o processo ou planta, outra junção de soma com a perturbação 2 e a saída. Além disso, junto à saída e interligada com a entrada, está a realimentação, no primeiro ponto de junção de soma, com a conexão do bloco transdutor de saída ou sensor.
Assim, como você pode imaginar, o uso de um sistema de controle em malha fechada pode trazer vantagens como a possibilidade de, mediante realimentação, trazer menor sensibilidade (ou quase nenhuma) a distúrbios externos e possíveis variações de parâmetros, internos no sistema. Todavia, sistemas de controle em malha fechada podem ser opções mais interessantes considerando custos e possível maior simplicidade de funcionamento, também geralmente estando menos sujeitos a perturbações na estabilidade. Na prática, este último acontece devido a ações de correção de erro que levam a oscilações na resposta do sistema. A decisão de uso por um tipo de sistema ou outro deverá considerar essas questões sob a perspectiva prática.
Exemplos Práticos
Tomaremos como exemplo a representação pautada na modelagem matemática, como sistemas de primeira ordem, segunda ordem e ordem superior.
Com relação à representação e à análise envolvendo a utilização do computador, é possível notar alguns passos comuns na prática. Veja, no diagrama de blocos a seguir, quais seriam as etapas para análise e projeto fundamentados num modelo do sistema prático.
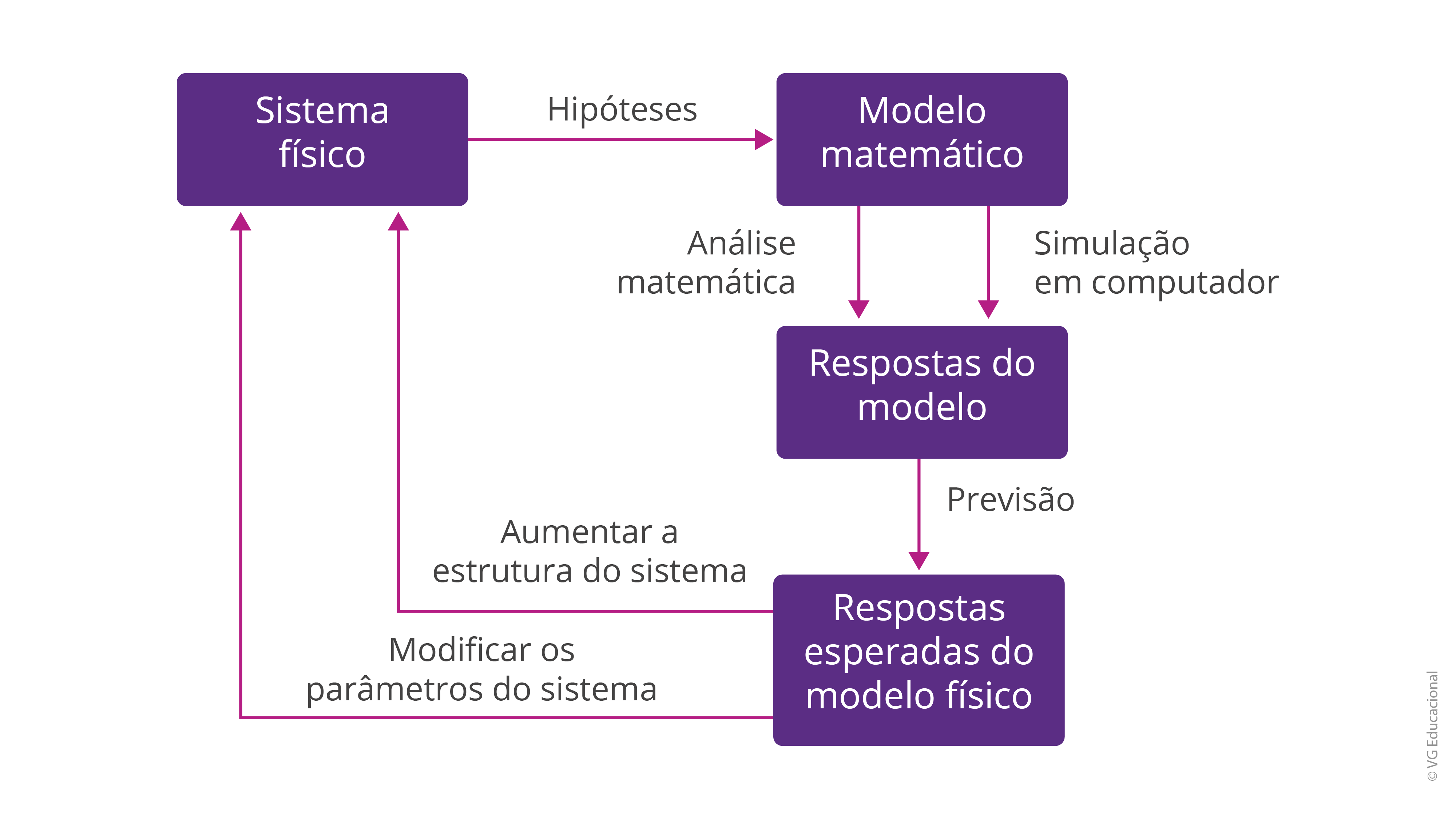
Fonte: Dorf (2018, p. 77).
#PraCegoVer: na figura, há um diagrama de blocos com o sistema físico, que, adicionado de hipóteses, permite obter o modelo matemático, sujeito à análise matemática e à simulação em computador, para a obtenção de resposta do modelo. Com isso, tem-se a previsão, com as respostas esperadas do modelo físico. Assim, permite-se decidir, ou não, por estratégias, como aumentar a estrutura do sistema e/ou modificar parâmetros do sistema.
Dentre as vantagens de utilização do computador, é possível destacar questões como: possibilidade de observação mais completa do sistema analisado sob todas as condições concebíveis; extrapolação de possíveis resultados com a simulação, pelo modelo, para previsão; diminuição de custos, ao final, para empresa ou indústria, por conta da minimização de gastos com testes, dentre outras. Ademais, é possível utilizar programas e linguagens de programação, como o MATLAB e o SCILAB, opção gratuita, que contam inclusive com toolboxes (conjuntos de ferramentas) específicas da área de controle. Entretanto existem outras opções gratuitas, como é o caso do Python, com várias bibliotecas da área. Todas essas opções possuem documentações on-line e vídeos no YouTube.
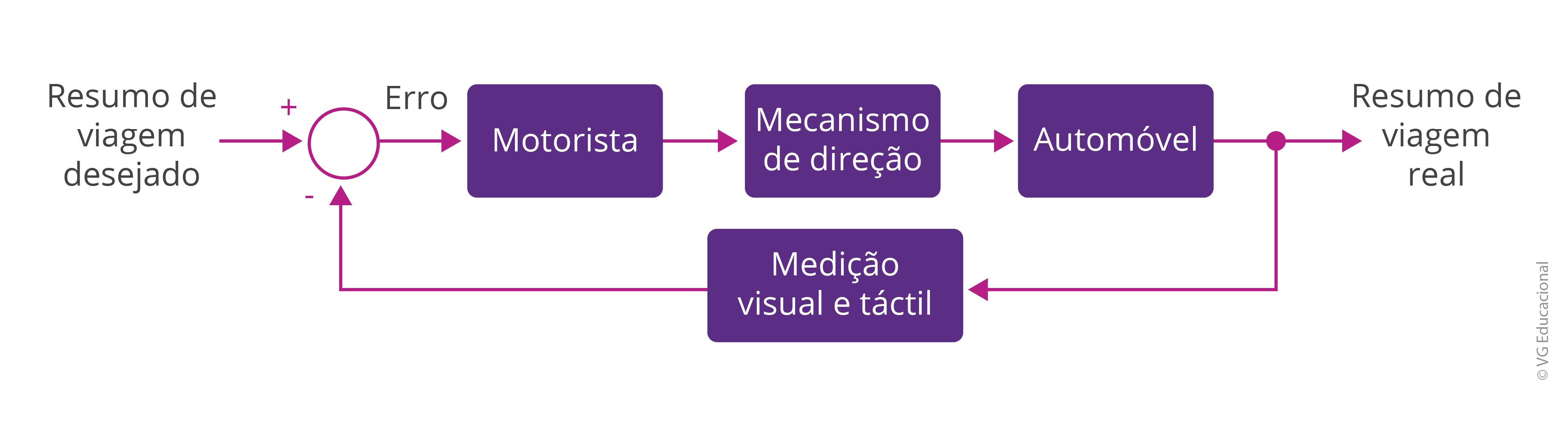
Retomando os exemplos de sistemas de controle, você se lembra do sistema de controle do automóvel, citado no subtópico sobre exemplos práticos acerca da introdução ao controle de sistemas? Poderíamos desenvolver um sistema de controle semelhante à representação a seguir, um sistema em malha fechada contando com utilização de um mecanismo de direção, medição de erro e processo de medição visual e táctil.
Fonte: Dorf (2018, p. 28).
#PraCegoVer: na figura, há um diagrama de blocos com a entrada, que é o rumo de viagem desejado, com sinal positivo em um somador, seguida pela entrada de um erro no bloco representado pelo motorista, que está em série com outros dois: o mecanismo de direção e o automóvel. Em seguida, aparece o rumo de viagem real na saída e a realimentação com medição visual e táctil.
Podemos destacar o fato de muitos carros contarem com sistemas assistidos, de direção e de freios — nesses, basicamente, é realizado algo muito semelhante à estrutura desse sistema. Perceba que o rumo desejável é comparado com o que está sendo seguido, na realidade, pelo carro. Isso gera uma medida de erro fisicamente coletada com base na medição visual e táctil, e espera-se que o carro passe a seguir o desejável ou o mais próximo possível disso.
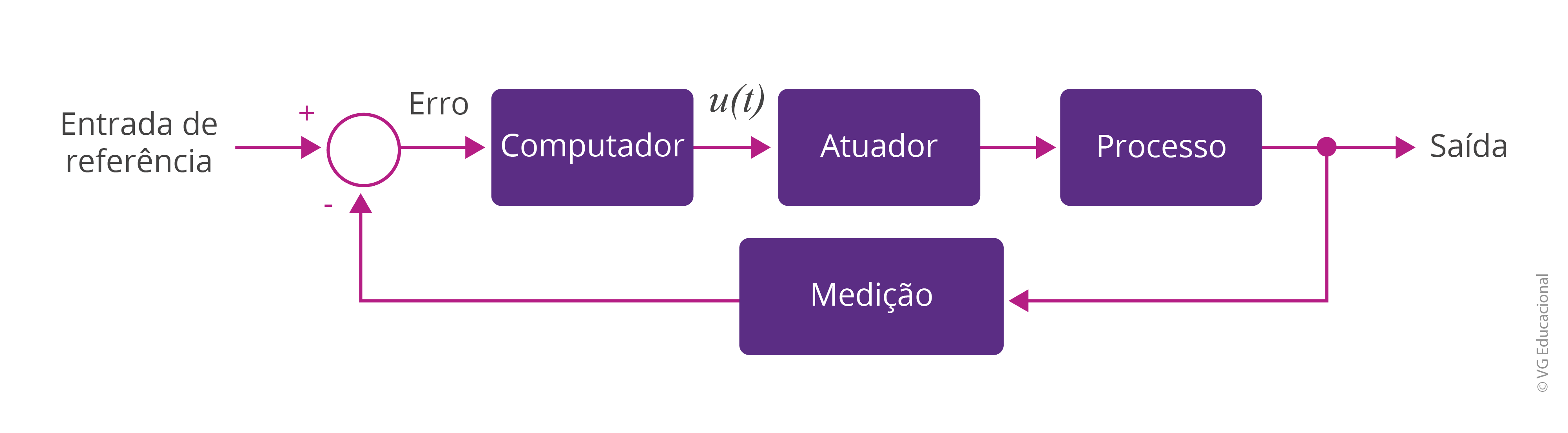
Considerando os avanços tecnológicos nos últimos anos, podemos destacar a forma geral com a qual o computador é inserido num sistema de controle em malha fechada, por exemplo. Veja, a seguir.
Fonte: Ogata (2010, p. 30).
#PraCegoVer: na figura, há um diagrama de blocos com entrada de referência. Em seguida, aparece o erro, o bloco computador, a entrada u(t), o atuador, o processo e a saída. Da saída, tem-se a realimentação com a medição, conectada à entrada e antes do erro.
Ademais, como exemplos de sistemas de controle em malha aberta, podemos citar equipamentos elétricos domésticos, como uma torradeira, e sistemas industriais que se aproximem de um sistema massa-mola-amortecedor. Além disso, veja que tanto o caso do regulador de nível quanto o do automóvel (apresentados no subtópico sobre exemplos práticos acerca da introdução ao controle de sistemas) são exemplos de sistemas de controle em malha fechada.
Num sistema de controle em malha fechada, alguns elementos são necessários, como o uso de um elemento para conexão da saída do sistema controlado junto ao controlador utilizado, também conhecida como conexão de realimentação do sistema.
Nesse sentido, acerca desses tipos de sistemas, é correto afirmar que:
Caro(a) estudante, daremos um passo importante no desenvolvimento de sistemas de controle, estudando as características da resposta dos sistemas dinâmicos, mais especificamente através da resposta transitória. Afinal, como já deve ter ficado claro, o entendimento de como o sistema a ser controlado funciona na prática é essencial no desenvolvimento de um sistema de controle efetivo. Começaremos com uma visão geral, englobando os principais conceitos da análise e, após, veremos exemplos práticos mais específicos. Vamos lá?
Visão Geral
Trataremos, para estudo, da resposta considerando a entrada sendo caracterizada por um sinal aperiódico, mais especificamente sinais como uma entrada degrau, rampa, aceleração e impulso ao longo do tempo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Commodo ullamcorper a lacus vestibulum sed arcu. Vel facilisis volutpat est velit egestas dui id ornare. Quis imperdiet massa tincidunt nunc pulvinar sapien et ligula.
Massa massa ultricies mi quis. Semper viverra nam libero justo. Sed tempus urna et pharetra pharetra massa massa. Nunc eget lorem dolor sed viverra. Quam pellentesque nec nam aliquam sem. Vulputate odio ut enim blandit volutpat maecenas volutpat. Maecenas accumsan lacus vel facilisis. Est sit amet facilisis magna. Tellus integer feugiat scelerisque varius morbi enim nunc faucibus.
Consideraremos a ordem do sistema analisado e, dessa forma, começaremos efetivamente pelo estudo de um sistema de primeira ordem, que pode ser um sistema elétrico, mecânico, térmico, enfim, qualquer tipo de sistema físico real, desde que seja possível a representação, considerada a quantidade de parâmetros a serem analisados, por exemplo.
Esse sistema pode ser, por exemplo, um circuito formado por um resistor e um capacitor, cuja relação entrada e saída pode ser dada por esta função de transferência:
\(\frac{C\left( s \right)}{R\left( s \right)}~=\frac{1}{Ts+1}~\)
A resposta a uma dada entrada é obtida inserindo-a junto à função, mais especificamente sua transformada de Laplace. Assim, para um degrau unitário, tem-se:
\(C\left( s \right)~=~\frac{1}{s}\frac{1}{Ts+1s}\)
Pela decomposição em frações parciais (manipulação matemática conveniente nesses tipos de análises), obtemos:
\(C\left( s \right)~=~\frac{1}{s}-\frac{T}{Ts+1}=\frac{1}{s}-\frac{1}{s+\left( 1/T \right)}\)
O próximo passo é realizar a transformada inversa de Laplace para obter o comportamento ao longo do tempo. Nesse caso, obtém-se:
\(c\left( t \right)~=~1-{{e}^{-t/T}}\), com \(t\ge 0\)
Caso t = T, com T sendo a constante de tempo do sistema, de acordo com a atenuação da resposta, ao longo do tempo e devido a aproximações das condições iniciais, tem-se que \(c\left( t \right)~=~1~-~{{e}^{-1}}=0,632\). Ou seja, quando t = T, o sistema alcançou 63,2% de sua variação total. Na verdade, ao plotar a resposta desse sistema ao longo do tempo, é fácil perceber que se trata de um sistema com curva de comportamento exponencial; assim, a partir de t = 5T, o sistema tenderá a manter sua resposta em 100%. Veja a próxima imagem.
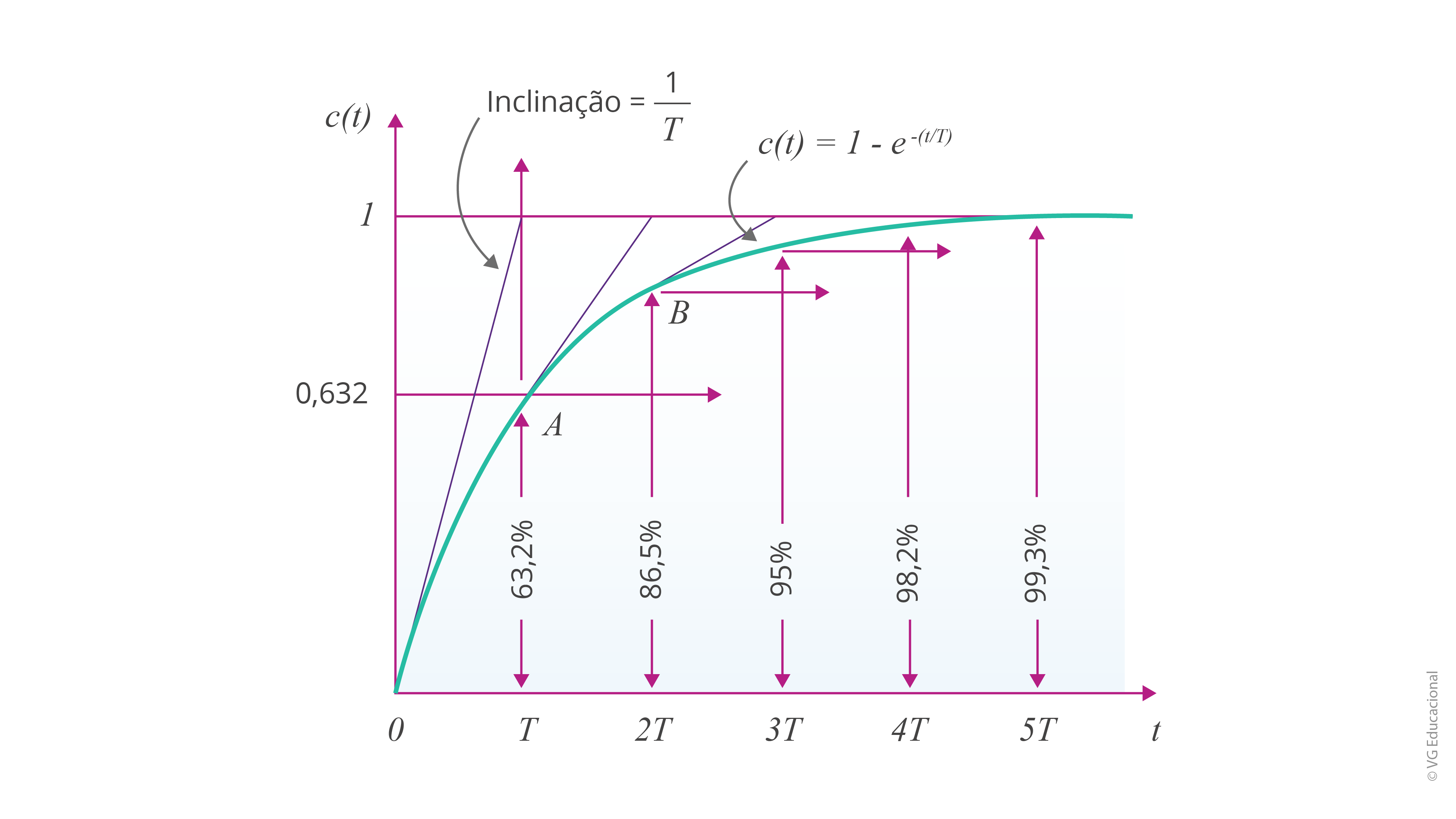
Fonte: Ogata (2010, p. 148).
#PraCegoVer: na figura, há um gráfico do tempo e da função de resposta c(t), \(~1-{{e}^{-\left( t/T \right)}}\), com as marcações de tempo de 0 até 5T, e, no eixo y, de 0 até 1, com 0,632. No ponto A, com tempo T, o sistema tem resposta com amplitude de 63,2%; em 2T, de 86,5%; em 3T, de 95%; 4T, de 98,2%; em 5T, de 99,3%. Além disso, está plotada no gráfico a reta de inclinação 1/T.
Nesse caso, percebemos que a resposta transitória perdura até um dado tempo, infinito, entretanto, na prática, estabelecemos, geralmente para esse tipo de caso, que, a partir de quatro constantes de tempo T, o sistema já está funcionando em regime permanente. Adicionalmente, a mesma análise é feita para qualquer entrada. Caso seja uma rampa unitária, sendo a transformada de Laplace 1/s², obtém-se, ao fim da expansão por frações parciais, que:
\(C\left( s \right)~=~\frac{1}{{{s}^{2}}}-\frac{T}{s}+\frac{{{T}^{2}}}{Ts+1}\)
Isso gera uma resposta de:
\(c\left( t \right)~=~t~-~T+T{{e}^{-t/T}}\), para \(t\ge 0\)
Mais ainda, cabe observarmos que o erro (e(t)) será:
\(e\left( t \right)~=~r\left( t \right)~-~c\left( t \right)~=~T\left( 1-{{e}^{-t/T}} \right)\)
E esse tende a T (para \(t~\to \infty \)). Já a resposta ao impulso unitário, sendo R(s) = 1, será:
\(C\left( s \right)~=~\frac{1}{Ts+1}\)
No domínio do tempo, obtém-se que:
\(c\left( t \right)~=~\frac{{{e}^{-t/T}}}{T}\) para \(t\ge 0\)
Além disso, é importante enfatizar que, basicamente, qualquer tipo de sistema pode ser analisado como um sistema de primeira ordem, desde que seja possível aproximá-lo como tal. Você já deve imaginar que em muitos casos essa aproximação não será válida e temos outra opção de modelagem que pode ser suficiente para a simplificação: a representação por meio de um sistema de segunda ordem.
REFLITA
Dado o contexto, você consegue imaginar situações que podem levar a um sistema físico, real, a ser representado por um sistema de segunda ordem, não um sistema de primeira ordem? Uma possibilidade é a quantidade de elementos, como indutores e capacitores, no caso de um sistema como um circuito elétrico.
Fonte: Elaborado pela autora.
A seguir, serão apresentados exemplos de sistemas de primeira ordem, incluindo sistemas físicos reais, para que você possa se inspirar durante sua atuação profissional e consiga ter uma ideia de qual caminho seguir. Vamos lá?
Exemplos Práticos
Os sistemas de nível de líquido podem ser exemplos bastante comuns, inclusive no dia a dia profissional, de sistemas representados como modelos de primeira ordem. Nesse sentido, considere como exemplo que: Q seja a vazão em volume durante o regime permanente (em m³/s); qi, um pequeno desvio devido a alguma perturbação, na vazão da entrada do sistema (em m³/s); qo, o mesmo, porém em relação à saída; H, a altura do nível em regime permanente (em m); h, um pequeno desvio nesse (também em m). Sendo esse sistema linear ou linearizado, a seguinte equação é válida.
\(Cdh~=~\left( {{q}_{i}}-{{q}_{o}} \right)dt\)
Onde, em função da resistência R, tem-se a variação da saída igual a:
\({{q}_{o}}=h/R\)
Isso faz com que esta relação seja válida:
\(RC\frac{dh}{dt}+h=R{{q}_{i}}\)
Pela transformada de Laplace, com condições iniciais nulas tem-se que:
\((RCs + 1)H(s) = RQi(s)\)
Sendo qi a entrada, e h, a saída, a função de transferência do sistema será:
\(\frac{H\left( s \right)}{{{Q}_{i}}\left( s \right)}=\frac{R}{RCs+1}\)
É possível fazer outra consideração para definir a relação entrada/saída, como considerar que a variação da vazão de saída seja a entrada, por exemplo. Na prática, uma dada função de transferência obtida não será a única opção de representação do sistema. A ideia central é buscar sempre uma possível representação matemática mais conveniente para manipulações matemáticas necessárias.
Como mencionado, a representação pautada numa função de transferência não é única, e isso pode ser facilmente visualizado na prática. Nesse sentido, considere novamente o sistema do exemplo prático anterior, de um sistema de controle de nível. Caso adotássemos qo como a saída e a entrada permanecesse a mesma, a variação de altura, qual seria a função de transferência capaz de representar o sistema?
Sendo \({{q}_{o}}=h/R\), como informado e dada a solicitação, que a função de transferência se torna G(s) = Qo(s)/H(s):
\(\frac{{{Q}_{o}}\left( s \right)}{H\left( s \right)}=\frac{h/R}{R}\)
Assim, obtemos que:
\(\frac{{{Q}_{o}}\left( s \right)}{{{Q}_{i}}\left( s \right)}=\frac{1}{RCs+1}\)
Até este ponto, nos pautamos na possibilidade de modelar matematicamente o sistema físico real mediante um sistema de primeira ordem, entretanto sabemos que isso pode não ser suficiente. Dessa forma, neste último tópico, nosso objetivo será modelar matematicamente os sistemas como modelo de segunda ordem, com mais exemplos práticos ao final. Vamos lá?
Visão Geral
Como exemplo, considere o seguinte servossistema (formado por um controlador e elementos para a representação da inércia e do atrito viscoso), cujo objetivo é controlar a posição de saída (c) a partir de uma dada entrada (r).
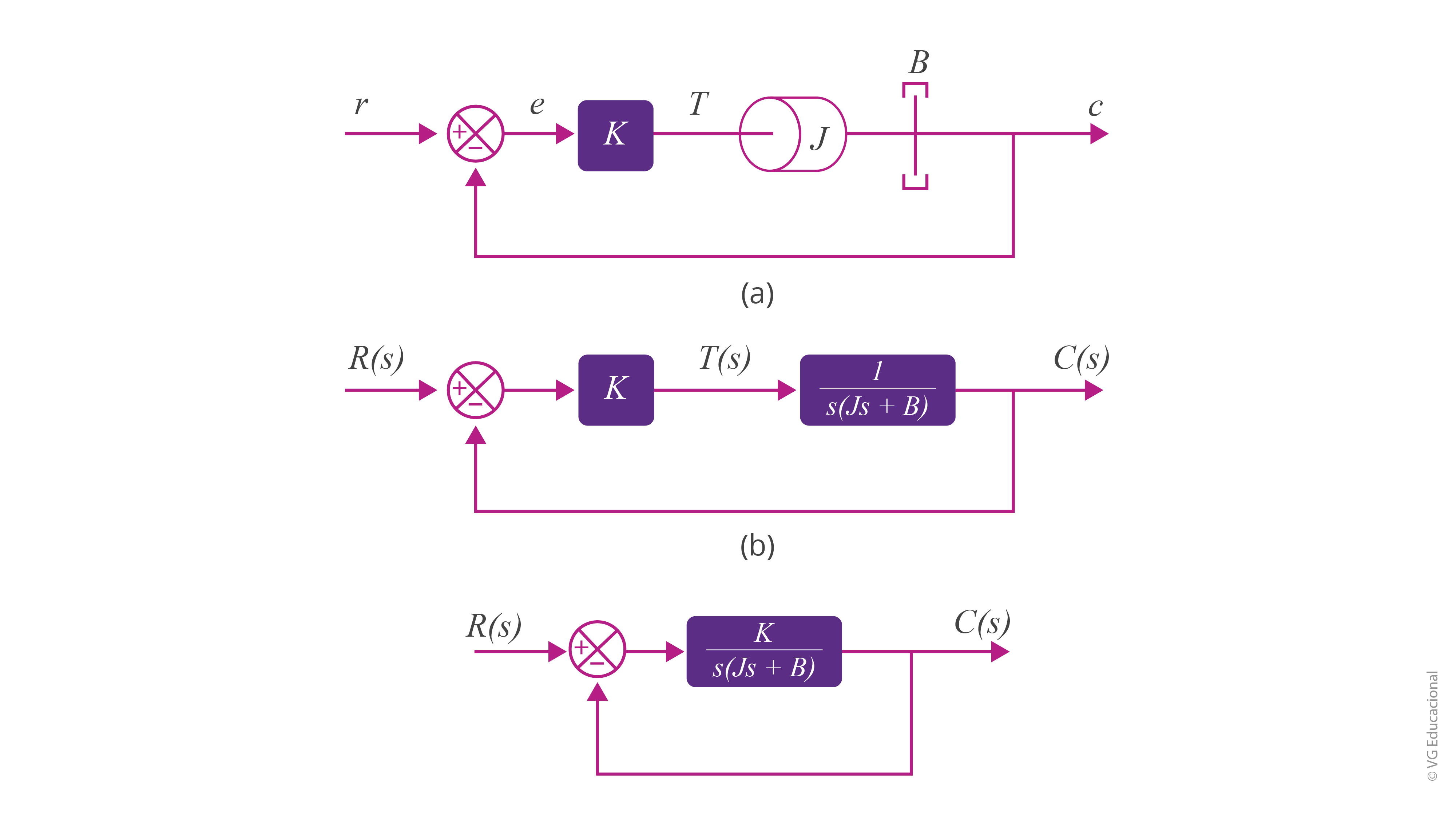
Fonte: Ogata (2010, p. 150).
#PraCegoVer: painel com três diagramas de bloco. No primeiro, tem-se o servossistema, com a entrada r e o erro, associado ao bloco K, que está em série com o elemento J e o elemento B, realimentados de maneira unitária. A saída é c. Em seguida, tem-se o diagrama de blocos do sistema em si, com R(s) de entrada, o bloco K, de saída T(s), e em série com o bloco 1/s(Js+B), realimentados unitariamente — sendo a saída igual a C(s). Por fim, tem-se o diagrama de blocos simplificado, com a entrada R(s), o bloco K/s(Js+B) e a saída C(s).
Para as condições e definições dadas, com T sendo o torque produzido pelo controlador, de ganho K, tem-se o possível equacionamento:
Jc’’ + Bc’ = T
Aplicando a transformada de Laplace, tem-se:
Js²C(s) + BsC(s) = T(s)
Isso gera a seguinte função de transferência:
\(\frac{C\left( s \right)}{T\left( s \right)}=\frac{1}{s\left( Js+B \right)}\)
Porém é mais conveniente representarmos em função da entrada, logo, tem-se que:
\(\frac{C\left( s \right)}{R\left( s \right)}=\frac{K}{J{{s}^{2}}+Bs+K}=\frac{K/J}{{{s}^{2}}+\left( B/J \right)s+K/J}\)
A resposta do sistema em malha fechada (considere o terceiro diagrama — Figura 1.9) pode ser obtida também, e o resultado será:
\(\frac{C\left( s \right)}{R\left( s \right)}=\frac{K}{J{{s}^{2}}+Bs+K}=\)
\(\frac{K/J}{\left[ s+\frac{B}{2J}+\sqrt{{{\left( \frac{B}{2J} \right)}^{2}}-\frac{K}{J}} \right]\left[ s+\frac{B}{2J}-\sqrt{{{\left( \frac{B}{2J} \right)}^{2}}-\frac{K}{J}} \right]}\)
Escrito dessa forma, com base nas raízes do polinômio do denominador, fica fácil perceber algumas características importantes, que nos auxiliarão a analisar a resposta do sistema e, inclusive, no projeto de um controlador para este, futuramente. Essas raízes são chamadas de polos, e esses são complexos conjugados caso B² - 4JK < 0 e reais se o contrário ou igual a zero. Para analisarmos a resposta transitória, mais especificamente, definiremos alguns fatores importantes: atenuação (\(\sigma \)), frequência natural não amortecida (\({{\omega }_{n}}\)) e coeficiente de amortecimento do sistema (\(\varsigma \)). A atenuação mostrará basicamente o comportamento da resposta ao longo do tempo, sendo matematicamente, nesse caso, definida por esta relação:
\(\frac{B}{J}=2\varsigma {{\omega }_{n}}=2\varsigma\) (7)
A frequência natural não amortecida à frequência da oscilação vista na resposta nesse período é definida por:
\({{\omega }^{2}}_{n}=K/J\) (8)
O coeficiente de amortecimento é a relação entre amortecimento devido a características reais do sistema (dado por B) e seu valor crítico (Bc), de forma que:
\(\varsigma ~=~\frac{B}{{{B}_{c}}}=\frac{B}{2\sqrt{JK}}\) (9)
Um sistema de segunda ordem possui, por conta desses três fatores, esta forma padrão:
\(\frac{C\left( s \right)}{R\left( s \right)}=\frac{{{\omega }_{n}}^{2}}{{{s}^{2}}+2\varsigma {{\omega }_{n}}s+{{\omega }_{n}}^{2}}\) (10)
Como o comportamento dinâmico pode ser representado principalmente a partir do coeficiente e da frequência, o sistema será:
- Subamortecido, caso a resposta transitória seja oscilatória, estando dentro da faixa de \(0~<\varsigma ~<~1\).
- Se \(\varsigma =0\), a resposta transitória não decai.
- Criticamente amortecido, caso \(\varsigma =1\).
- Superamortecido, caso \(\varsigma >1\).
Outro ponto de atenção: no caso de um sistema subamortecido, os polos de malha fechada do sistema serão do tipo complexo e conjugados, localizados, graficamente, no semiplano esquerdo do plano s. Além disso, denominamos um novo parâmetro para entender o comportamento oscilatório durante a resposta transitória nesses casos: a frequência natural amortecida (\({{\omega }_{d}}\)), que é aquela com a qual o sistema oscila nesse ponto.
Assim como fizemos para o sistema de primeira ordem, analisaremos, como exemplo acerca desse ponto, qual seria a resposta ao degrau unitário. Para isso, mais especificamente, considere o seguinte sistema de segunda ordem, apresentado pelo próximo diagrama de blocos.
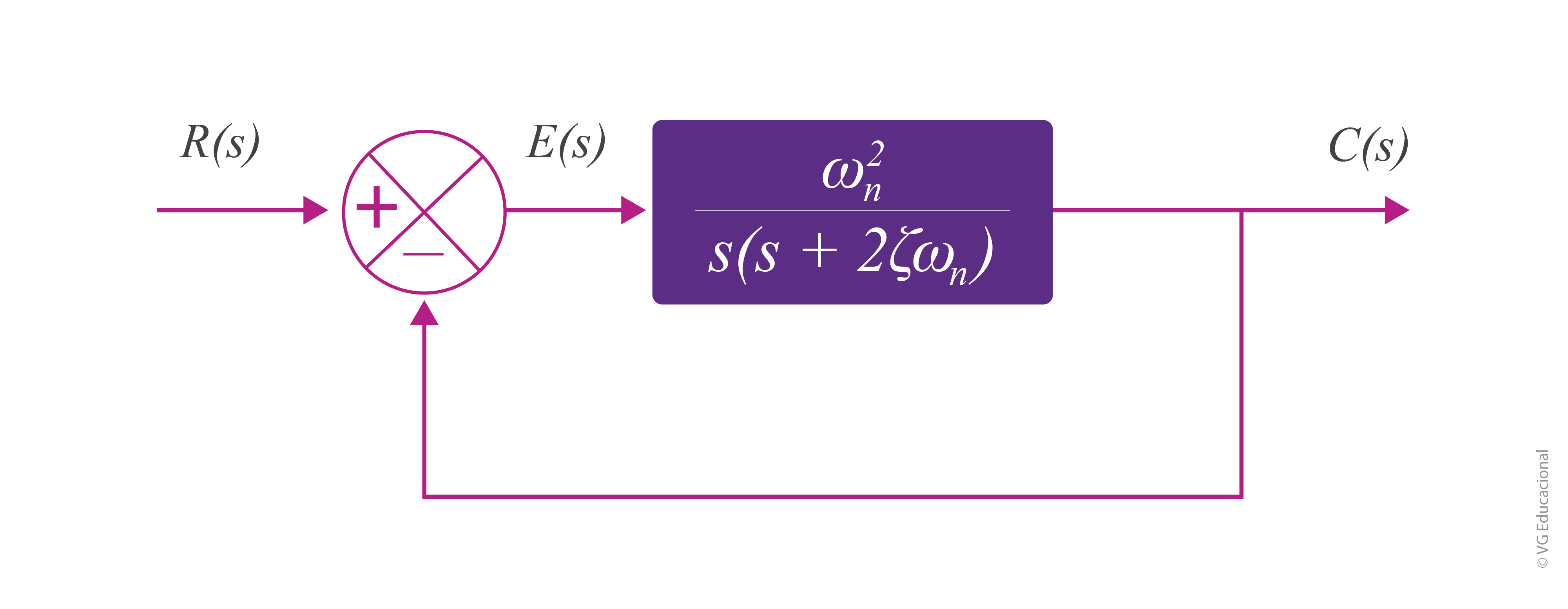
Fonte: Ogata (2010, p. 151).
#PraCegoVer: diagrama de blocos com R(s) de entrada, E(s) de erro, em entrada com o bloco \(\frac{{{\omega }_{n}}^{2}}{s\left( s+2\varsigma {{\omega }_{n}} \right)}\) (ômega n ao quadrado, sobre s, vezes s, mais 2 vezes csi, vezes ômega n). Além disso, a saída é C(s), e a realimentação é unitária.
Sendo o sistema subamortecido, a função de transferência se torna a seguinte, com \(0~<\varsigma ~<~1\):
\(\frac{C\left( s \right)}{R\left( s \right)}=\frac{{{\omega }_{n}}^{2}}{\left( s+\varsigma {{\omega }_{n}}+j{{\omega }_{d}} \right)\left( s+\varsigma {{\omega }_{n}}-j{{\omega }_{d}} \right)}\)
Tem-se, ainda, que a frequência das oscilações será:
\({{\omega }_{d}}~=~{{\omega }_{n}}\sqrt{1~-~{{\varsigma }^{2}}}\) (11)
Com a entrada, mais efetivamente, a saída será:
\(C\left( s \right)~=~\frac{{{\omega }_{n}}^{2}}{\left( {{s}^{2}}+2\varsigma {{\omega }_{n}}s+{{\omega }_{n}}^{2} \right)s}\)
Ou, ainda, pela transformada de Laplace:
\(C\left( s \right)~=~\frac{1}{s}-\frac{s+2\varsigma {{\omega }_{n}}}{{{s}^{2}}+2\varsigma {{\omega }_{n}}s+{{\omega }_{d}}^{2}}=\)
\(\frac{1}{s}-\frac{s+\varsigma {{\omega }_{n}}}{\left( s+2\varsigma {{\omega }_{n}} \right){}^\text{2}+{{\omega }_{d}}^{2}}-\frac{\varsigma {{\omega }_{n}}}{\left( s+\varsigma {{\omega }_{n}} \right){}^\text{2}+{{\omega }_{d}}^{2}}\)
A resposta será, no domínio do tempo:
\(c\left( t \right)~=~1-\frac{{{e}^{-\varsigma {{\omega }_{n}}t}}}{\sqrt{1-{{\varsigma }^{2}}}}sen\left( {{\omega }_{d}}t+t{{g}^{-1}}\left( \frac{\sqrt{1-{{\varsigma }^{2}}}}{\varsigma } \right) \right)\)
para \(t\ge 0\)
Caso o sistema seja, por outro lado, criticamente amortecido (o que, na prática, equivale aos dois polos serem iguais), tem-se que a saída é, considerando a transformada de Laplace:
\(C\left( s \right)~=~\frac{{{\omega }_{n}}^{2}}{\left( s+{{\omega }_{n}} \right){}^\text{2}s}\)
No domínio do tempo, obtém-se que:
\(c\left( t \right)~=~1-{{e}^{-{{\omega }_{n}}t}}\left( 1+{{\omega }_{n}}t \right)\), para \(t\ge 0\)
Por fim, para o caso superamortecido (como no caso em que dois polos sejam reais, negativos e diferentes), obtém-se com a transformada de Laplace:
\(C\left( s \right)~=~\frac{{{\omega }_{n}}^{2}}{\left( s+\varsigma {{\omega }_{n}}+{{\omega }_{n}}\sqrt{{{\varsigma }^{2}}-1} \right)\left( s+\varsigma {{\omega }_{n}}-{{\omega }_{n}}\sqrt{{{\varsigma }^{2}}-1} \right)s}\)
No domínio do tempo, obtém-se:
\(c\left( t \right)~=~1+\frac{{{\omega }_{n}}}{2\sqrt{{{\varsigma }^{2}}-1}}\left( \frac{{{e}^{-{{s}_{1}}t}}}{{{s}_{1}}}-\frac{{{e}^{-{{s}_{2}}t}}}{{{s}_{2}}} \right)\), para \(t\ge 0\)
Com \({{s}_{1}}=\left( \varsigma +\sqrt{\varsigma {}^\text{2}-1} \right){{\omega }_{n}}\) e \({{s}_{2}}=\left( \varsigma -\sqrt{\varsigma {}^\text{2}-1} \right){{\omega }_{n}}\), a resposta incluirá termos do tipo exponenciais decrescentes. Na próxima figura, é possível ver a resposta desse sistema escolhido como exemplo para aplicação do degrau unitário na entrada.
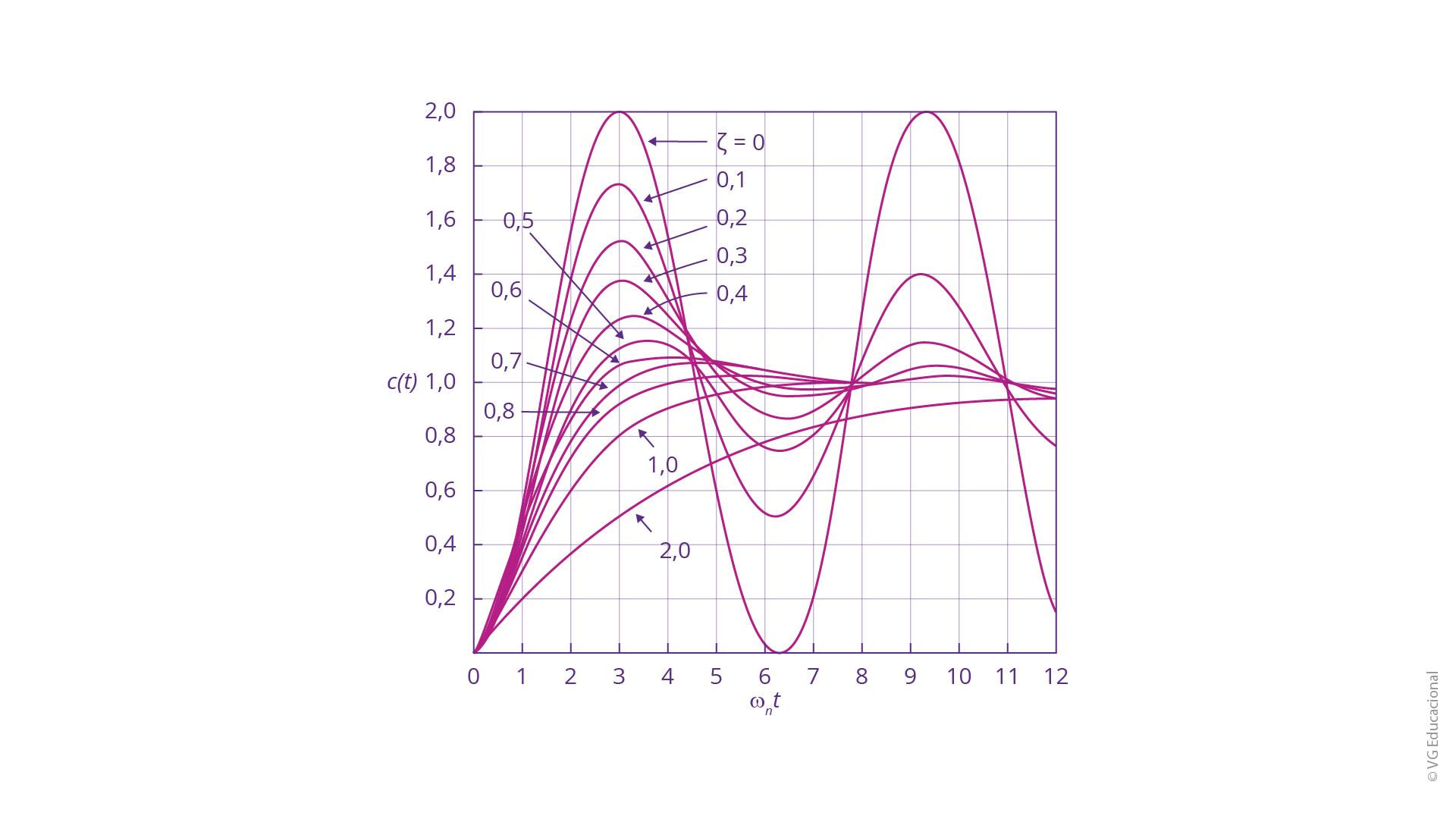
Fonte: Ogata (2010, p. 154).
#PraCegoVer: gráfico de \({{\omega }_{n}}t\) (ômega n, vezes t) e c(t), com diferentes curvas, considerando a variação de \(\varsigma \) (csi), de 0 até 2. Para 0, as oscilações são as de maiores amplitudes; para 0,1, a amplitude diminui, e isso vai acontecendo até 0,6, quando a resposta passa a ter um pico só, que vai diminuindo de amplitude até atingir a menor, em 2.
Quanto menor o coeficiente de amortecimento, maior a amplitude da oscilação vista, ao passo que quando esse, no caso apresentado, for igual a 2, por exemplo, a oscilação já não existirá. Todavia, é importante salientar que a melhoria na resposta transitória vai muito além de trabalhar somente com esse coeficiente. Nesse sentido, para as especificações de um sistema de controle para um sistema dessa natureza, estabelecemos os seguintes parâmetros (OGATA, 2010):
A próxima figura apresenta esses parâmetros plotados junto à resposta gráfica do sistema. É apresentada, inclusive, uma possível tolerância aceitável; sobretudo, é importante observar que, para alguns tipos de sistemas em específico, isso pode ser modificado.
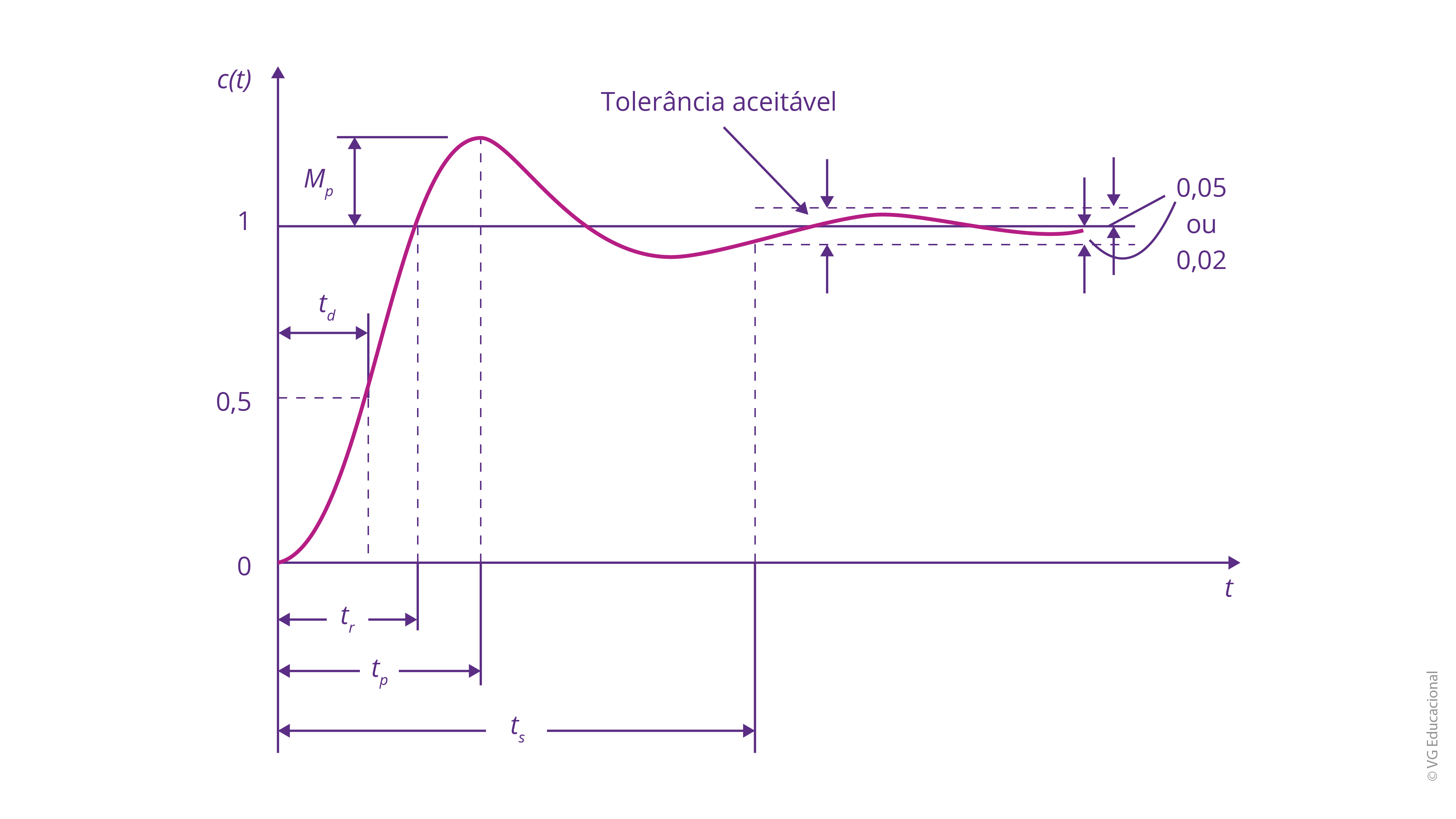
Fonte: Ogata (2010, p. 155).
#PraCegoVer: gráfico de tempo e c(t), com a curva de um dado sistema de segunda ordem apresentado. Nessa curva, estão marcados o tempo de atraso, de 0 até 0,5; o tempo de subida, de 0 até 1, e o tempo de acomodação, de 0 até 0,02 de tolerância (sendo que está de 0,05 ou 0,02). Além disso, mostra-se o sobressinal, de 1 até o pico máximo da resposta.
Por fim, veremos, adiante, em visão geral, exemplos práticos de sistemas físicos que podem ser modelados por meio de sistemas de segunda ordem, bem como utilizados para parâmetros de controle, esses tempos e sobressinal vistos.
Exemplos Práticos
Tomando como exemplo, inicialmente, sistemas mecânicos, como vimos, existem certos tipos de sistemas do tipo massa-mola que podem ser modelados por meio de um sistema de primeira ordem. Entretanto, considerando especificamente modelos massa-mola ainda, observa-se que quando precisamos considerar parâmetros simultaneamente, como as forças às quais está sujeito um sistema em deslocamento, um sistema de segunda ordem pode ser utilizado. Quer ver como? Imagine ser necessário modelar matematicamente um sistema formado por um sistema massa-mola-amortecedor localizado numa plataforma que se locomove, um carro, por exemplo. Considerando o princípio de se tratar de um sistema translacional, podemos utilizar como base a Segunda Lei de Newton e obter o modelo matemático com base no somatório das forças, igualado à massa do conjunto vezes a aceleração desse. A função de transferência, ao final, embora ainda dependa de quem consideramos como entrada e saída nesse sistema, será dada em função de parâmetros como coeficiente de atrito, elasticidade da mola e massa.
Considerando como exemplo prático um sistema elétrico, mais precisamente um circuito, observamos que um circuito RLC, ou seja, um circuito formado por resistores e, ao menos, um indutor e um capacitor, é um exemplo relativamente comum de sistema real modelado como um sistema de segunda ordem. Inclusive, se necessário considerar mais elementos conectados, pode ser conveniente analisar o sistema por meio de impedâncias complexas, a fim de simplificar a análise e, consequentemente, o modelo matemático obtido ao final.
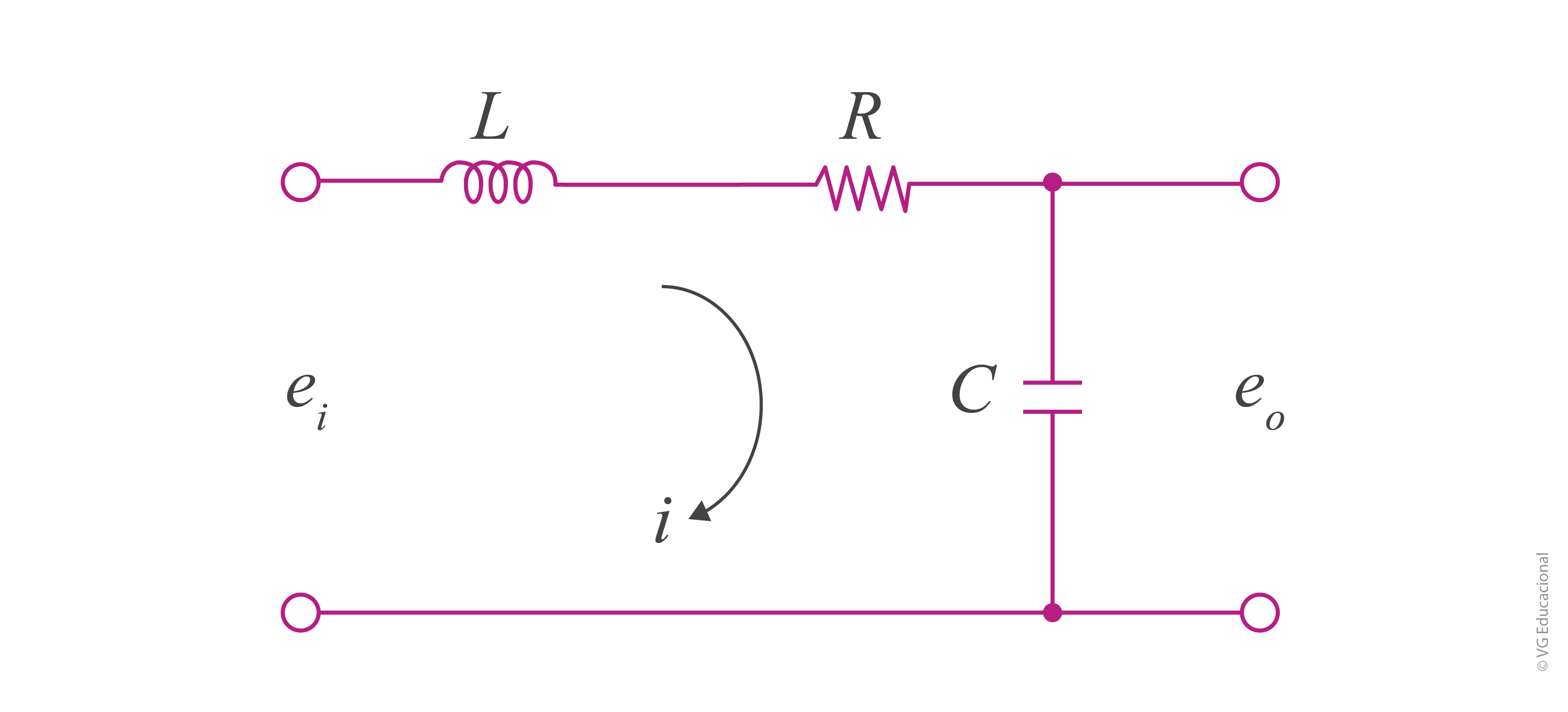
Os circuitos elétricos, presentes nos mais diversos tipos de equipamentos, são exemplos relativamente comuns de sistemas físicos reais para os quais, frequentemente, precisaremos considerar o uso de um modelo de segunda ordem para a modelagem matemática. Nesse sentido, considere o circuito elétrico a seguir.
Qual seria uma possível função de transferência a ser utilizada por um controlador projetado para esse sistema? Para facilitar, considere que algumas informações são conhecidas e que o sistema estava inicialmente desligado, o que permite considerar condições iniciais como nulas.
Utilizando as leis de Kirchoff, mais especificamente a lei de tensão, conseguimos obter as seguintes equações:
\(L\frac{di}{dt}+Ri+\frac{1}{C}\mathop{\int }_{{}}^{{}}i~dt~=~{{e}_{i}}\)
\(\frac{1}{C}\mathop{\int }_{{}}^{{}}i~dt~=~{{e}_{o}}\)
O próximo passo será aplicar a transformada de Laplace. Assim, o resultado será, com as condições iniciais nulas, correspondente a:
\(LsI\left( s \right)~+~RI\left( s \right)~+~\frac{1}{C}\frac{1}{s}I\left( s \right)~=~{{E}_{i}}\left( s \right)\)
\(\frac{1}{C}\frac{1}{s}I\left( s \right)~=~{{E}_{o}}\left( s \right)\)
Tomando a tensão de entrada como a entrada do sistema e a tensão de saída como a saída deste, uma possível função de transferência será:
\(\frac{{{E}_{o}}\left( s \right)}{{{E}_{i}}\left( s \right)}=\frac{1}{LC{{s}^{2}}+RCs+1}\)
Ademais, é importante ressaltar, como brevemente mencionado, que, em alguns casos, será necessário utilizar um modelo matemático de ordem superior. Especialmente nesses casos, que representam a maior parte dos sistemas na prática, sem simplificações, o uso do computador nas análises será primordial.
Sistemas de controle (aula 4) sistemas de primeira ordem
Canal: Eng. Luis Cesar Emanuelli
Comentário: nessa videoaula, é possível aprender mais detalhes, incluindo alguns exemplos práticos, de como representamos sistemas físicos como sistemas de primeira ordem, o que é uma aproximação válida em muitos casos.

Controle de processos industriais: princípios e aplicações
Autor: Claiton Moro Franchi
Editora: Érica; Saraiva
Capítulo: 2
Ano: 2011
ISBN: 9788536818282
Comentário: esse livro é destinado ao estudo de como são feitos os principais tipos de sistemas destinados ao controle de processos industriais. Sugere-se a leitura do capítulo 2, onde é possível estudar mais detalhes acerca das principais características dinâmicas identificadas em sistemas reais e como trabalhamos com sistemas de primeira ordem.
Disponível na Biblioteca Virtual.
Bem, vê-se que sistemas de controle, especialmente considerando avanços tecnológicos e questões como a promoção das iniciativas da Indústria 4.0, têm se tornado cada vez mais comuns, independentemente do porte da indústria. Portanto, é fundamental para o exercício da profissão entender como esses sistemas funcionam. Tivemos uma visão geral do que são e como funcionam os sistemas de controle, quais são as estratégias para representação desses, incluindo o estudo de quais são os elementos mais comuns que fazem parte, e, por fim, iniciamos, nos dois últimos tópicos, um ponto igualmente importante: o entendimento sobre como os sistemas em geral se comportam na prática.
Relembre, sobretudo com relação à última parte, que, em alguns casos, será possível realizar algumas aproximações e desconsiderar variações do sistema ao longo do tempo, por exemplo.
DORF; R. C. Sistemas de controle moderno. 13. ed. Rio de Janeiro: LTC, 2018.
FRANCHI; C. M. Controle de processos industriais: princípios e aplicações. São Paulo: Érica; Saraiva, 2011. (Disponível na Biblioteca Virtual).
GRINGS - transformada de Laplace - aula 1. [S. l.: s. n.], 2016. 1 vídeo (20 min). Publicado pelo canal omatematico.com. Disponível em: https://www.youtube.com/watch?v=s0JR9JchSqs&list=PLE6qFDd4x9w--UTAIL5Qw23Dm_ZxaRUzF. Acesso em: 18 mar. 2022.
NISE; N. S. Engenharia de sistemas de controle. 7. ed. Rio de Janeiro: LTC, 2017.
OGATA; K. Engenharia de controle moderno. 5. ed. São Paulo: Pearson Prentice Hall, 2010. (Disponível na Biblioteca Virtual).
SISTEMAS de controle (aula 04) sistemas de primeira ordem. [S. l.: s. n.], 2017. 1 vídeo (12 min). Publicado pelo canal Eng. Luis Cesar Emanuelli. Disponível em: https://www.youtube.com/watch?v=2oOTkSRnaG4. Acesso em: 18 mar. 2022.