Controle de Sistemas
Estabilidade, simulação de sistemas dinâmicos e controladores PID
Tempo de leitura do conteúdo estimado em 1 hora e 20 minutos.
Olá, estudante! Tudo bem?
Entender como analisar a estabilidade de sistemas reais, de comportamentos dinâmicos, é de fundamental importância para o exercício da profissão e para ações como o desenvolvimento de um sistema de controle e automação. Além disso, o projeto de um sistema de controle utilizará, geralmente, algumas estratégias gerais para obter a melhor configuração possível do sistema controlado.
Assim, no presente estudo, você entenderá o que é a estabilidade de um sistema dinâmico e como efetuar análises para atestar tal propriedade, aplicadas a sistemas reais. Em seguida, você verá como realizar simulações computacionais para visualizar o comportamento dinâmico dos sistemas físicos. Por fim, encerraremos nossos estudos com dois tópicos dedicados ao controlador proporcional, integral e derivativo (PID), que é o principal tipo de controlador, nas mais diversas aplicações industriais, entendendo como este funciona e como ajustá-lo.
Diante disso, eu te convido a embarcar nesta jornada de estudos, que contribuirá de forma ampla para a sua formação. Vamos lá?
Partimos do pressuposto de que existirão três requisitos principais para o projeto de um sistema de controle: a atenção à resposta transitória, a estabilidade e possíveis erros em regime permanente, quando esse sistema já apresenta seu comportamento estacionário. Além disso, muitos pesquisadores e as próprias aplicações práticas convergem para uma ideia principal de que a estabilidade é a especificação mais importante entre essas opções. Caso um sistema seja instável, por exemplo, sua resposta transitória e os erros vistos, durante o regime permanente, terão menos relevância frente a essa condição indesejada. Mais ainda, percebe-se que um sistema instável não poderá ser projetado para atender a um determinado tipo de resposta transitória específica ou mesmo para atender a um outro requisito, de erro em regime permanente, por exemplo.
Assim, iniciaremos com uma visão geral do que é a estabilidade e como avaliá-la, para sistemas em geral. Na sequência, daremos ênfase a exemplos práticos da realização de análises desse tipo. Vamos lá?
Visão Geral
A resposta total de um dado sistema, independente de outras questões práticas deste, dependerá da soma entre a resposta forçada (solução da equação diferencial ou, ainda, possíveis diferenças vistas para uma dada entrada, com condições iniciais nulas) e a resposta natural (aquela referente às condições iniciais):
\(c\left( t \right)~=~{{c}_{forada}}\left( t \right)~+~{{c}_{natural}}\left( t \right)\) (1)
E é partindo dessa ideia que conseguimos definir os três principais tipos de situações: estabilidade, instabilidade e estabilidade marginal.
Um sistema linear invariante no tempo é estável se a resposta natural tende a zero à medida que o tempo tende a infinito. Um sistema linear invariante no tempo é instável se a resposta natural aumenta sem limites à medida que o tempo tende a infinito. Um sistema linear invariante no tempo é marginalmente estável caso a resposta natural não decaia nem aumente, mas permaneça constante ou oscile à medida que o tempo tende a infinito (NISE, 2017, p. 450).
Assim, podemos observar que a presença da resposta forçada, à medida que a natural tenderá a zero, está associada à própria definição de estabilidade de um sistema, embora seja importante observar, também, a este ponto, que é difícil, em muitos casos, distinguir o que faz parte da resposta natural do que compreende na resposta forçada do sistema. Nesse sentido, é comum definir-se que um sistema será estável caso toda entrada limitada seja capaz de levar a uma determinada saída, também limitada, o que nos leva a uma definição de um tipo de sistema, em específico: os sistemas Bibo (do inglês, bounded-input, bounded-output).
De maneira similar, entende-se que um sistema será instável caso alguma entrada limitada seja capaz de produzir uma dada saída ilimitada, que, junto com a definição de um sistema estável anterior, poderá auxiliar no entendimento da estabilidade marginal. Um sistema, nesse último caso, será estável para algumas entradas, limitadas, e instável para outras. Ou seja, partindo da resposta total, um sistema será estável caso toda entrada limitada seja capaz de produzir uma saída limitada e é instável se existir alguma entrada limitada capaz de gerar uma saída ilimitada. Pode parecer confuso, a princípio, mas à medida que desenvolvermos os critérios matemáticos para análise de estabilidade, esses conceitos apresentados ficarão mais claros.
Falando, então, em meios matemáticos e formas de se analisar a estabilidade, dado um modelo matemático de um sistema, como sua função de transferência, é fundamental citarmos o critério de Routh-Hurwitz, que vem de 1905 e é utilizado até hoje, a partir da aplicação de dois passos básicos: a construção de uma tabela de dados (também conhecida como tabela de Routh) e a interpretação desta. Basicamente, nesse último momento, analisaremos quantos polos da função de transferência do sistema em malha fechada estão localizados no semiplano esquerdo, no semiplano direito e no próprio eixo \(j\omega \), no plano s. O processo de construção da tabela de Routh é feito rotulando-se as linhas pelos valores das potências de s, partindo das potências maiores do denominador da função de transferência do sistema conectado em malha fechada, que, a partir de agora, chamaremos, simplesmente, de função de transferência de malha fechada.
Em seguida, preencheremos com o coeficiente de potência mais alta de s, ainda do polinômio do denominador, e listaremos, horizontalmente e na primeira linha, os coeficientes restantes, pulando, ainda, um coeficiente. Na segunda linha da tabela, listaremos, horizontalmente, a partir da segunda maior potência de s vista naquele polinômio, incluindo os coeficientes saltados anteriormente e os demais elementos da tabela, não preenchidos, serão preenchidos pelo negativo do determinante de elementos inscritos nas duas linhas anteriores, divididos pelo elemento da primeira coluna, acima da linha analisada (NISE, 2017). Parece um pouco complicado, mas com a visualização do sistema genérico a seguir e, em seguida, de sua tabela correspondente, ficará mais fácil.
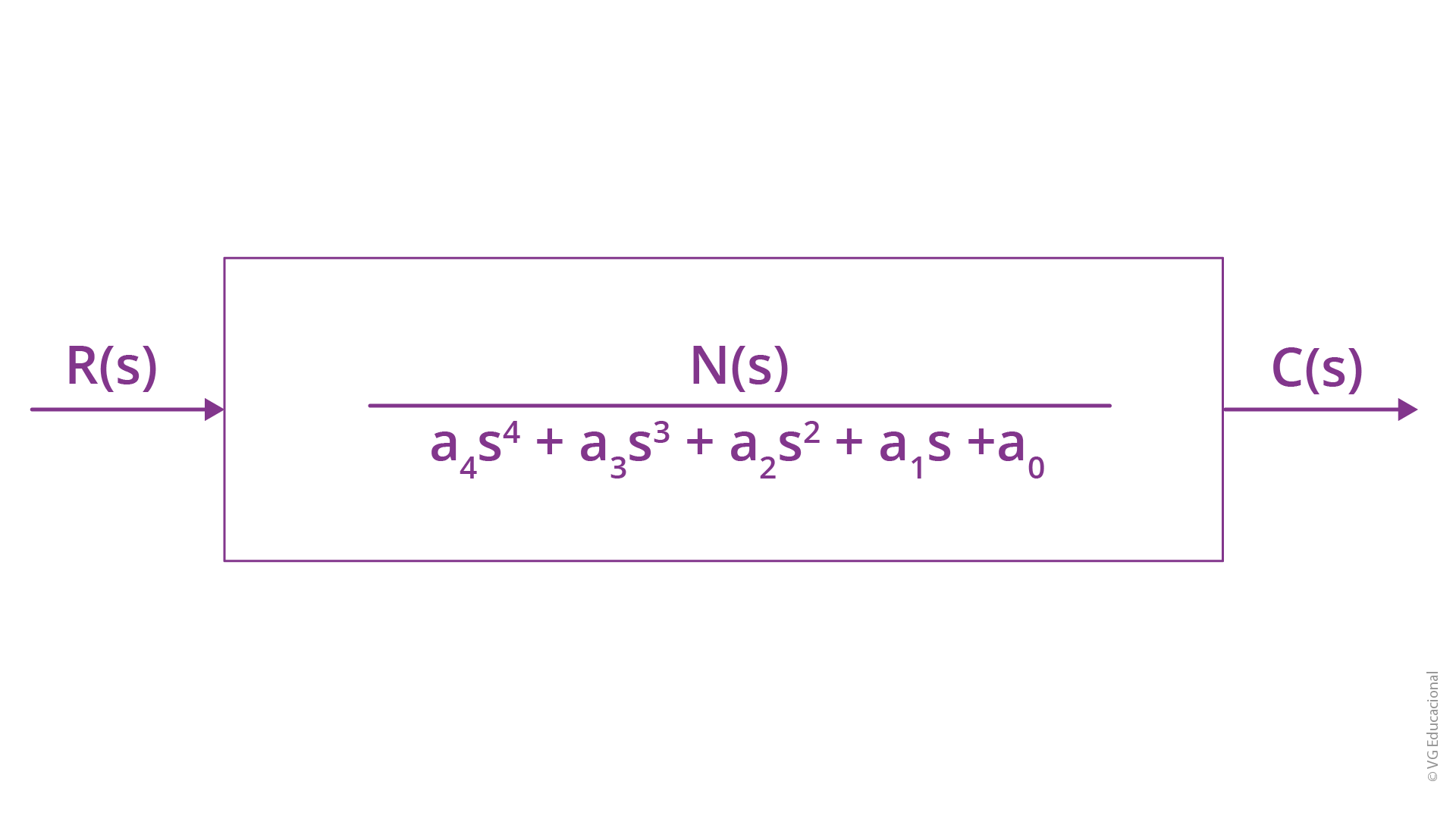
Fonte: Nise (2017, p. 455).
#PraCegoVer: diagrama de blocos com R(s) na entrada, o bloco \(N\left( s \right)/{{a}_{4}}{{s}^{4}}+{{a}_{3}}{{s}^{3}}+{{a}_{2}}{{s}^{2}}+{{a}_{1}}s+{{a}_{0}}\) (N s sobre a 4 vezes s elevado à quarta, mais a 3 vezes s elevado à terceira, mais a 2 vezes s elevado ao quadrado, mais a 1 vez s, mais a 0) e C(s) na saída.
Considerando a maior potência, 4, veja como ficaria a tabela nesse caso genérico.
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 5 linhas mais 4 colunas. Na primeira linha, tem-se \({{s}^{4}}\) (s elevado à quarta), \({{a}_{4}}\), \({{a}_{2}}\) e \({{a}_{0}}\). Na segunda, tem-se s³ (s elevado ao cubo), \({{a}_{3}}\), \({{a}_{1}}\) e 0. Na terceira linha, tem-se s² (s elevado ao quadrado), \(\frac{-\left| \begin{matrix} {{a}_{4}} & {{a}_{2}} \\ {{a}_{3}} & {{a}_{1}} \\\end{matrix} \right|}{{{a}_{3}}}={{b}_{1}}\) (menos determinante de a4, a2, a3 e a1 sobre a3, igual a b1), \(\frac{-\left| \begin{matrix} {{a}_{4}} & {{a}_{0}} \\ {{a}_{3}} & 0 \\\end{matrix} \right|}{{{a}_{3}}}={{b}_{2}}\) (menos determinante de a4, a0, a3 e 0, sobre a3, igual a b2) e \(\frac{-\left| \begin{matrix} {{a}_{4}} & 0 \\ {{a}_{3}} & 0 \\\end{matrix} \right|}{{{a}_{3}}}=0\) (menos determinante de a4, 0, a3 e 0, sobre a3, igual a 0). Na quarta, tem-se s¹ (s elevado a 1), \(\frac{-\left| \begin{matrix} {{a}_{3}} & {{a}_{1}} \\ {{b}_{1}} & {{b}_{2}} \\\end{matrix} \right|}{{{b}_{1}}}={{c}_{1}}\) (menos determinante de a3, a1, b1 e b2, sobre b1, igual a c1), \(\frac{-\left| \begin{matrix} {{a}_{3}} & 0 \\ {{b}_{1}} & 0 \\\end{matrix} \right|}{{{b}_{1}}}=0\) (menos determinante de a3, 0, b1 e 0, sobre b1, igual a 0) e \(\frac{-\left| \begin{matrix} {{a}_{3}} & 0 \\ {{b}_{1}} & 0 \\\end{matrix} \right|}{{{a}_{3}}}=0\) (menos determinante de a3, 0, b1 e 0, sobre b1, igual a 0). Na quinta linha, tem-se \({{s}^{0}}\) (s elevado a 0), \(\frac{-\left| \begin{matrix} {{b}_{1}} & {{b}_{2}} \\ {{c}_{1}} & 0 \\\end{matrix} \right|}{{{c}_{1}}}={{d}_{1}}\) (menos determinante de b1, b2, c1 e 0, sobre c1, igual a d1), \(\frac{-\left| \begin{matrix} {{b}_{1}} & 0 \\ {{c}_{1}} & 0 \\\end{matrix} \right|}{{{c}_{1}}}=0\) (menos determinante de b1, 0, c1 e 0, sobre c1, igual a 0) e \(\frac{-\left| \begin{matrix} {{b}_{1}} & 0 \\ {{c}_{1}} & 0 \\\end{matrix} \right|}{{{c}_{1}}}=0\) (menos determinante de b1, 0, c1 e 0, sobre c1, igual a 0).
Levando em consideração, agora, o processo de interpretação, fundamental para finalizarmos a análise de estabilidade, é possível observar, de antemão, que a tabela vista, até o momento, nos permite analisar sistemas que possuem polos localizados nos semiplanos esquerdo e direito. Todavia, caso seja necessário interpretar polos imaginários, por exemplo, será preciso alguns passos a mais, que veremos mais adiante. Assim, como primeira regra, é possível observar que a quantidade de raízes no semiplano direito corresponde à quantidade de mudanças de sinal da primeira coluna da tabela. Nesse sentido, ainda, você poderá observar que o sistema é estável, caso a função de transferência em malha fechada de um dado sistema possuir todos os polos no semiplano esquerdo do plano s. Do contrário, estando esses polos no semiplano direito, o sistema é instável.
Agora, para analisarmos inclusive alguns casos especiais, vamos à aplicação e à análise em alguns exemplos. Considere, inicialmente, que desejamos analisar a estabilidade de um sistema que possui a seguinte função de transferência em malha fechada:
\[G\left( s \right)~=~\frac{10}{{{s}^{5}}+2{{s}^{4}}+3{{s}^{3}}+6{{s}^{2}}+5s+3}\]
Nesse caso, ao obtermos a tabela, como vimos até o momento, obteríamos uma divisão por zero e, por conta disso, estabeleceremos uma constante, \(\epsilon \) (épsilon), para substituir o zero na primeira coluna. O resultado disso será:
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 6 linhas e 4 colunas. Na primeira linha, tem-se \({{s}^{5}}\) (s elevado a 5), 1, 3 e 5. Na segunda linha, tem-se \({{s}^{4}}\) (s elevado à quarta), 2, 6 e 3. Na terceira linha, tem-se s³ (s elevado ao cubo), \(\epsilon \) (épsilon), 7/2 (7 sobre 2) e 0. Na quarta linha, tem-se s² (s elevado ao quadrado), \(6\epsilon -7/\epsilon \) (6 vezes épsilon menos 7, sobre épsilon), 3 e 0. Na quinta linha, tem-se s¹ (s elevado a 1), \(\left( 42\epsilon -49-6\epsilon {}^\text{2} \right)/\left( 12\epsilon -14 \right)\) (42 vezes épsilon menos 49 menos 6 vezes épsilon ao quadrado, sobre 12 vezes épsilon menos 14), 0 e 0. Na sexta linha, tem-se \({{s}^{0}}\) (s elevado a zero), 3, 0 e 0.
Caso \(\epsilon \) seja escolhido positivo, visualizaremos uma mudança de sinal da linha s³ para a s² e de s² para s¹, o que permite concluir que existem dois polos no semiplano direito e, assim, trata-se de um sistema instável. Por outro lado, se você escolhesse essa constante como um valor negativo, por outro lado, a mesma conclusão seria obtida, porém a partir de um caminho diferente.
Uma outra possibilidade é obter uma linha inteira com zeros, resultado de fatoração do denominador quando há a presença de pelo menos um polinômio par, o que implicará novas estratégias, diferentes do que vimos até o momento. Para entender, considere que um dado sistema possui a seguinte função de transferência em malha fechada:
\[G\left( s \right)~=~\frac{10}{{{s}^{5}}+7{{s}^{4}}+6{{s}^{3}}+42{{s}^{2}}+8s+56}\]
A construção da tabela, nesse caso, contará, também, com algumas manipulações matemáticas, por conveniência, para facilitar a finalização. Assim, na segunda linha, multiplicam-se os coeficientes por 1/7 e paramos na terceira linha, já que esta é a formada por zeros. Agora, considerando especificamente a diferença devido à terceira linha, orienta-se, nesses casos, para retornar à linha imediatamente acima, da de zeros, e a partir desta determinar um polinômio auxiliar, com coeficientes a partir dessa linha acima, começando com a potência de s da coluna da identificação correspondente e pulando uma potência de s. Em nosso exemplo, o resultado será:
\[{{s}^{4}}+6{{s}^{2}}+8\]
O próximo passo é o cálculo da derivada desse novo polinômio, em relação à s:
\[4s³ + 12s + 0\]
O resultado será utilizado, enfim, para preencher a linha zerada. Ao final, com esse exemplo então, concluímos que não existem polos no semiplano direito e existe um padrão da distribuição dos polos, nesses casos, que nos permitem concluir que (NISE, 2017):
A imagem a seguir traz um resumo dessa distribuição de raízes, capazes de gerarem polinômios pares. A este ponto ainda é importante observar que, ao analisarmos a tabela de Routh nestes casos, devemos analisar a situação dos polos do polinômio par (se há ou não polinômios no semiplano da direita). Com isso, caso não existam polos no semiplano da direita, por exemplo, não existirão no lado esquerdo também, por conta da simetria:
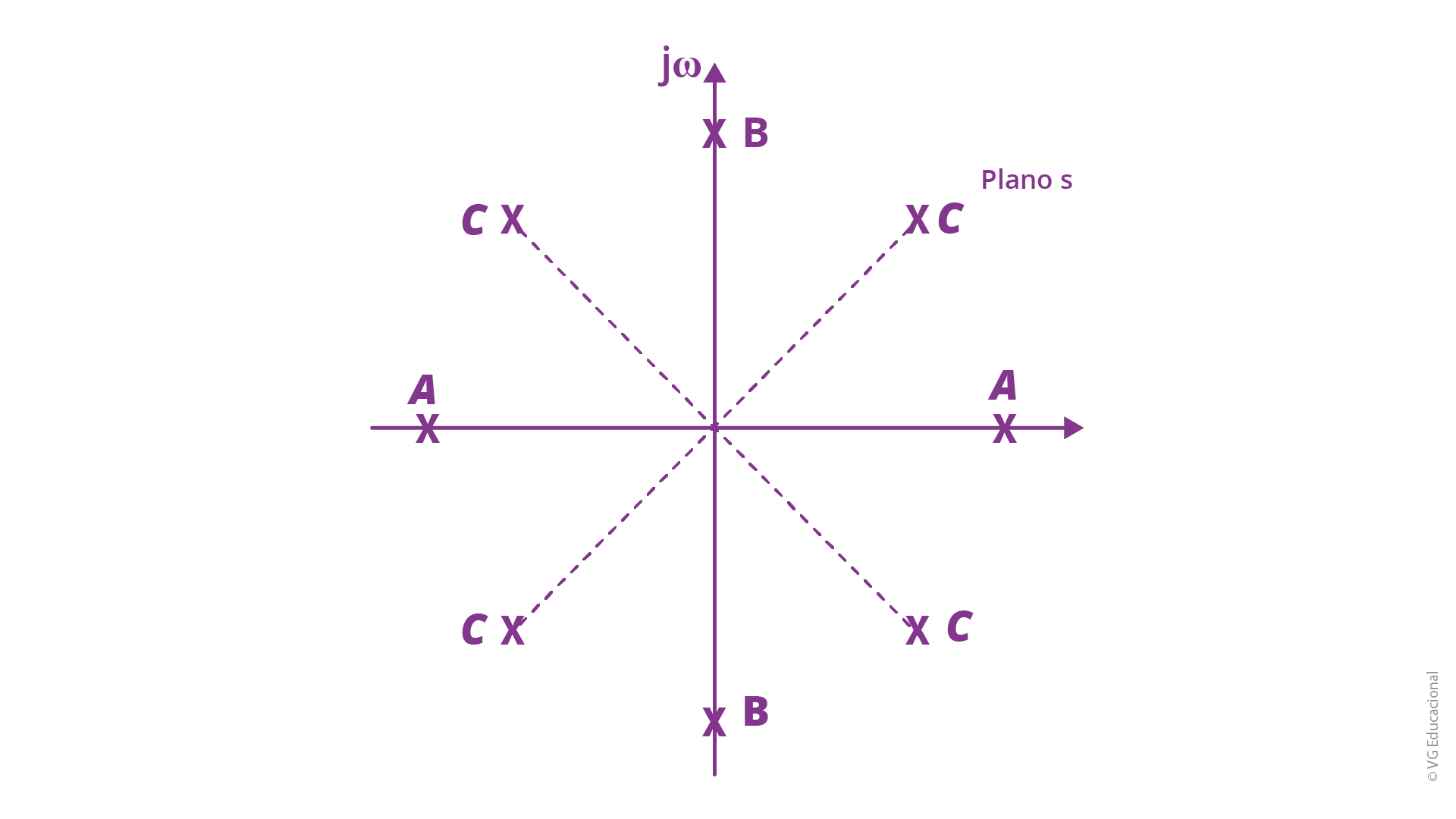
Fonte: Nise (2017, p. 462).
#PraCegoVer: plano s com os pares de polos A, B e C, sendo os polos C localizados nas partes de cima e de baixo, tanto no semiplano direito quanto no esquerdo; os polos A no eixo \(\sigma \) e os polos B no eixo \(j\omega \) (j ômega).
Ademais, saiba que o critério de Routh-Hurwitz oferece, inclusive, uma prova facilmente percebida de que mudanças no ganho de um sistema de controle, com realimentação, é capaz de ocasionar diferenças na resposta transitória, pois haverá modificações nas posições dos polos em malha fechada. Na próxima subseção, apresento alguns exemplos finais, focando na resposta que pode ser observada de acordo com a estabilidade (ou não) do sistema analisado, trazendo um exemplo de como podemos estabelecer o ganho de um dado sistema real para que este seja estável, instável ou marginalmente estável.
Exemplos Práticos
Bem, até o presente momento, foi possível visualizar como analisar a estabilidade, porém precisamos discutir, também, outro importante ponto: afinal, o que a estabilidade, a instabilidade ou mesmo a estabilidade marginal significam no comportamento de um sistema físico, real? Tomando como exemplo a resposta, ao longo do tempo, ao degrau unitário de um sistema estável, nota-se, em comparação a de um sistema instável, que as oscilações tenderão a diminuir com o tempo. O seguinte sistema de controle representa um exemplo de sistema estável, juntamente com a representação dos polos da função de transferência em malha fechada e a resposta ao longo do tempo, denotando que, de fato, após cerca de 15 segundos, a amplitude das oscilações diminui consideravelmente, até praticamente zerar, em torno de 25 segundos:
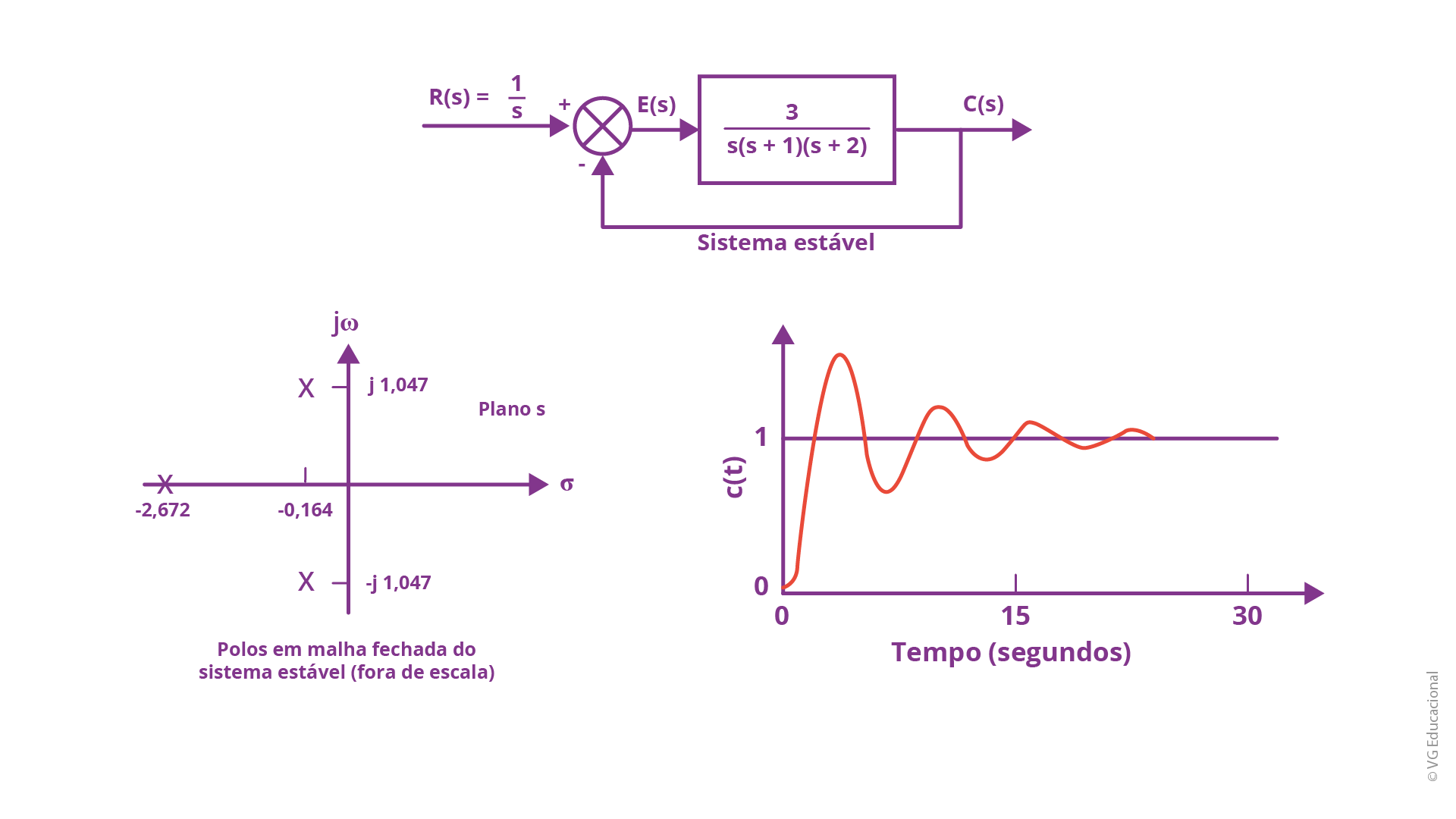
Fonte: Adaptada de Nise (2017).
#PraCegoVer: na parte superior, tem-se o diagrama de blocos do sistema, com R(s) = 1/s (R s igual a 1 sobre s) na entrada, o erro E(s) (E s), o bloco 3/s(s+1)(s+2) (3 sobre s vezes s mais 1 vez s mais 2), a saída C(s) (C s) e esta está, ainda, conectada à entrada pelo somador. Na parte de baixo, tem-se, do lado esquerdo, os polos em malha fechada plotados no plano s, com -2,672; -0,164; j1,047 e -j1,047. No lado direito, tem-se a resposta do sistema, c(t) (c t), ao longo do tempo, com as oscilações maiores no início e a diminuição destas, sendo a resposta vista de 0 a 30 s.
Por outro lado, na próxima imagem, tem-se o exemplo de uma planta que representa um sistema de controle em malha fechada, porém referente a um sistema instável. Note que, ao invés da amplitude das oscilações diminuir, esta aumenta à medida que o tempo passa:
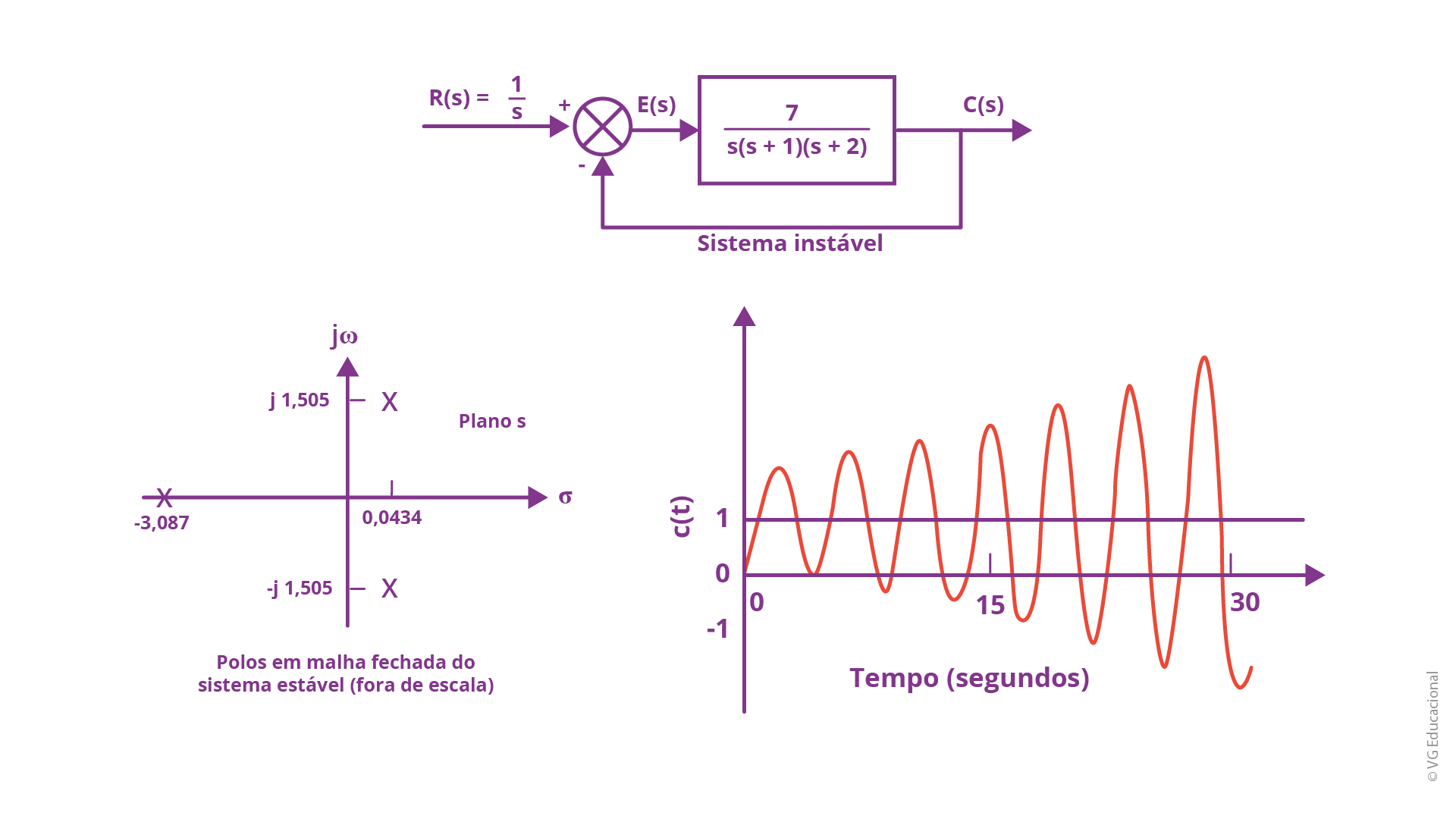
Fonte: Adaptado de NISE (2017, p. 453)
#PraCegoVer: na parte superior, tem-se o diagrama de blocos do sistema, com R(s) = 1/s (R s igual a 1 sobre s) na entrada, o erro E(s) (E s), o bloco 7/s(s+1)(s+2) (7 sobre s vezes s mais 1 vez s mais 2), a saída C(s) (C s), estando esta conectada à entrada pelo somatório. Na parte de baixo, do lado esquerdo, tem-se a plotagem dos polos de malha fechada no plano s, com os pontos 3,087; j1,505; -j1,505 e 0,0434. Por fim, do lado direito, tem-se a resposta, c(t) (c t), ao tempo do tempo, em segundos, demonstrando as oscilações que aumentam de amplitude, de 0 até 30 segundos.
Além disso, outro ponto importante que pode ser retomado aqui é que, em um sistema marginalmente estável, a resposta vista, ao longo do tempo, será constante ou oscilatória. Assim, as oscilações vistas inicialmente poderão permanecer com a mesma amplitude, por exemplo. Os polos da função de transferência em malha fechada estarão, ainda, tanto no semiplano da esquerda quanto localizados no eixo \(j\omega \), podendo ser, ou não, múltiplos neste último.
Agora, para encerrarmos este tópico, suponha que seja necessário determinar a faixa de valores de ganho (K), para que o sistema de função de transferência a seguir, conectado em malha fechada (unitária), seja estável, marginalmente estável e instável, para K > 0:
\[G\left( s \right)~=~\frac{K}{s\left( s+7 \right)\left( s+11 \right)}\]
O primeiro passo será, é claro, obter a função de transferência em malha fechada
\[G\left( s \right)~=~\frac{K}{{{s}^{3}}+18{{s}^{2}}+~77s+K}\]
e, em seguida, é possível construir a tabela de Routh:
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 4 linhas e 3 colunas, sendo, na primeira linha, s³ (s elevado ao cubo), 1 e 77; na segunda linha, s² (s ao quadrado), 18 e K; na terceira linha, s¹ (s elevado a 1), (1386-K)/18 (1.368 menos K sobre 18); e, na quarta linha, \({{s}^{0}}\) (s elevado a zero) e K.
Como K > 0, os elementos, na primeira coluna, serão sempre positivos, com exceção ao elemento de s¹, que pode ser tanto positivo quanto negativo ou, ainda, nulo, a depender do valor de K. Agora, precisaremos considerar essas possibilidades. Com isso, se K < 1.386, de fato, assim todos os termos serão positivos e, como não existirá mudanças de sinal, conclui-se que o sistema analisado possui três polos no semiplano da esquerda. Logo, trata-se de um sistema estável e essa é a restrição do ganho para que o sistema tenha estabilidade.
Todavia, perceba que para K > 1.386, o termo de s¹, da primeira coluna, será negativo, e como haverá duas mudanças de sinal teremos dois polos no semiplano da direita e um polo no semiplano da esquerda, o que permite concluir que o sistema, nessas condições, seria instável.
Por fim, a última possibilidade é que o ganho K seja ajustado em 1.386, gerando uma linha completa de zeros, o que implica que haveria polos no eixo \(j\omega \) e, assim, seria necessário manipular matematicamente, como fizemos no último exemplo do subtópico 2.1.1. Retornaremos, nesse caso, à linha s², substituímos K pelo seu valor assumido e, assim, o seguinte polinômio é criado,
\[18s² + 1.386\]
cuja derivada é
\[36s + 0\]
e, utilizando-o para refazer a tabela de Routh para o caso, obtém-se:
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 4 linhas e 4 colunas. Na primeira linha, s³ (s elevado ao cubo) salta a coluna 2, 1 e 77. Na segunda linha, s² (s ao quadrado) salta a coluna 2, 18 e 1.386. Na terceira linha, \({{s}^{1}}\) (s elevado a 1), 0 (substituído) e 36. Na quarta linha, \({{s}^{0}}\) (s elevado a zero) salta a coluna 2 e 1.386.
Dessa forma, perceba que não haverá mudanças de sinal da linha s² (a partir do polinômio par anterior), e isso permanece para a tabela inteira. O polinômio par possui duas raízes sobre o eixo e, além disso, observa-se que essas raízes possuem multiplicidade unitária, que, junto com os sinais constantes, permite observar que há uma raiz remanescente no semiplano esquerdo do plano s e, assim, o sistema é marginalmente estável.
Um sistema físico pode ser modelado de diversas maneiras, entre elas como um sistema linear, com resposta invariável ao longo do tempo. Já sua estabilidade pode ser avaliada analisando o modelo matemático, mais precisamente a partir da posição no plano s dos polos de malha fechada.
Considerando essas informações, assinale a alternativa correta.
Seja na análise específica acerca da estabilidade de um sistema dinâmico ou mesmo para estratégias mais simples, como visualizar a resposta dinâmica de um dado sistema, a utilização de software ou, ainda, de linguagens de programação, no desenvolvimento de algoritmos, será fundamental. A crescente utilização dos próprios software ou do desenvolvimento de algoritmos se dá especialmente quando ocorrem situações como a impossibilidade de se considerar o sistema analisado como um modelo matemático linear ou mesmo já partindo da complexidade adicionada, naturalmente, frente ao desenvolvimento tecnológico dos últimos anos. Assim, a este ponto, teremos uma visão geral do papel dos software, tomando como exemplo o Matlab, o Scilab e o Octave e, em seguida, alguns exemplos práticos.
Visão Geral
O Matlab é um dos software mais utilizados no contexto para análise de sistemas dinâmicos e de sistemas de controle, em geral, embora não seja uma opção gratuita. Neste, podemos ressaltar o desenvolvimento de algoritmos, a partir de funções básicas ou que fazem parte de outros conjuntos de funções mais específicos, entretanto o maior destaque deve ser dado para as toolboxes — conjuntos de ferramentas —, destinadas, exclusivamente, para a análise de sistemas de controle.
Por fim, tem-se um conjunto de funções nessa toolbox, destinado às análises lineares, em que existirão ferramentas tanto no domínio do tempo quanto no da frequência.
O Scilab, por sua vez, é um software gratuito, bastante semelhante ao Matlab, de certa forma, em termos da linguagem, tendo boa quantidade de recursos disponíveis. Além da possibilidade de desenvolvimento de algoritmos, assim como no software anterior, aqui podemos destacar a Xcos, um editor gráfico para o desenvolvimento de modelos de sistemas dinâmicos variados, que permite a visualização completa da simulação, tanto no domínio do tempo quanto em outros tipos de análises, com modelos já pré-estabelecidos de circuitos mecânicos automotivos, dentre outros.
Por fim, o Octave é um tipo de linguagem computacional diretamente compatível com Matlab, com grande quantidade de funções muito semelhantes, podendo ser utilizado para a computação matemática, em geral, o que inclui a possibilidade de análise e simulação de sistemas dinâmicos. Algumas das funções de controle em geral, vistas no Matlab, podem ser utilizadas diretamente neste.
Exemplos Práticos
Tomando como exemplo então a utilização da toolbox Control System Toolbox, do Matlab, suponha que nosso objetivo aqui fosse representar um sistema dinâmico, linear. A função tf permite estabelecer a função de transferência do sistema físico analisado e, para utilizá-la, fazemos
\[\text{sys = tf(num,den)}\]
com num sendo a variável para apresentação do polinômio do numerador e den para a apresentação do polinômio do denominador. Caso tivéssemos a seguinte função de transferência,
\[G\left( s \right)~=~\frac{1}{2{{s}^{2}}+3s+4}\]
então faríamos computacionalmente:
num = 1;
den = [2, 3, 4];
sys = tf(num,den)
Sem o ponto e vírgula, ao final do comando com a variável sys, será possível visualizar, na tela, a função de transferência criada. Caso quiséssemos visualizar a resposta ao degrau unitário do sistema com a função de transferência apresentada, o seguinte comando poderia ser dado:
\[\text{stepplot(sys)}\]
Por outro lado, caso fosse desejável criar a representação pelo espaço de estados, o seguinte comando deve ser utilizado:
\[\text{sys = ss(A,B,C,D)}\]
com A, B, C e D sendo as representações dos coeficientes no espaço de estados nas formas matriciais, a partir de:
\[x'~=~Ax+Bu\]
\[y~=~Cx+Du\]
Agora, vamos considerar os mesmos processos vistos nesses exemplos práticos, porém utilizando o software Scilab. De forma bastante similar ao Matlab, o primeiro passo será definir matricialmente, ou por meio dos polinômios, o numerador e o denominador da função de transferência desejada. Caso a função de transferência que representasse o modelo fosse igual a
\[G\left( s \right)~=~\frac{7}{{{s}^{3}}+3{{s}^{2}}+2s+7}\]
computacionalmente faríamos:
\[\text{num = 7;}\]
\[\text{den = s^3+(3*s^2)+2*s+7;}\]
\[\text{sys = syslin([], num, den)}\]
Outro ponto interessante é que aplicando essa variável criada, que representa a função de transferência, à função plz(), tem-se o esboço dos polos e dos zeros dessa função. Já com relação à representação no espaço de estados, semelhantemente também ao Matlab, faremos:
\[\text{[A,B,C,D] = abcd(sl)}\]
SAIBA MAIS
Olá, estudante! A este ponto, convido você a visualizar o passo a passo da simulação realizada por meio do Matlab, de um tanque, com uma equação diferencial não linear, de primeira ordem.
Para saber mais, acesse a seguir:
Ademais, a utilização de bibliotecas em Python, como no exemplo citado anteriormente, vem ganhando bastante espaço, seja pela pluralidade de funções já implementadas, mas, especialmente, pelo fato de que se trata de documentações abertas, disponíveis on-line e de fácil acesso. Um exemplo é a biblioteca python-control, uma biblioteca para análise e desenvolvimento de sistemas de controle com realimentação, para análises no domínio da frequência e por meio da representação no espaço de estados.
Até o momento, ficou clara a importância da utilização da simulação na análise de sistemas dinâmicos, incluindo a possibilidade de auxílio no projeto de sistemas de controle, certo? Pensando nisso, acompanhe o pequeno estudo de caso a seguir.
Guilherme, estudante de Engenharia Elétrica, precisa analisar o comportamento dinâmico não linear de um pêndulo simples, um clássico sistema estudado. Ele fará essa análise, aproximando-o como um modelo linear, a ser processado pelo software Matlab, disponibilizado por sua escola.
Considerando que você estivesse no lugar de Guilherme, com os seus conhecimentos até o momento, qual estratégia você utilizaria?
Como mencionado anteriormente, o Matlab conta com um conjunto de ferramentas (toolbox) de controle de sistemas, que permite o uso de diversas funções para a análise de sistemas dinâmicos: a toolbox Control System Toolbox. Dessa forma, esta seria uma ótima opção para o estudante e, nesse caso, de visualização da resposta. Os passos básicos poderiam ser: criação da função de transferência linear obtida e obtenção da resposta ao degrau unitário, pelas funções tf e stepplot, respectivamente.
Certo, mas afinal de contas: como implementamos o agente que fará o controle em um sistema controlado? A resposta dessa pergunta está em uma metodologia largamente utilizada, inclusive em controladores industriais: o controlador proporcional, integral e derivativo (mais conhecido como controlador PID).
Em 1922, a Sperry Gyroscope Company instalou um sistema automático de direção, que utilizava elementos de compensação e controle adaptativo para melhorar o desempenho. [...] Foi seu desenvolvimento teórico aplicado à condução automática de navios que levou ao que hoje chamamos de controladores proporcional, integral e derivado (PID), ou controladores de três modos (NISE, 2017, p. 33).
Assim, veja que a utilização dos controladores PID contribuiu imensamente para tantos avanços tecnológicos que vemos atualmente, em termos do controle e automação de sistemas em geral, bem como das diversas possibilidades de implementar esses controladores.
REFLITA
A este ponto você deve estar se perguntando: Como é possível implementar um controlador PID? Bem, veja que essa pergunta pode ser respondida de mais de uma maneira, a depender de características, inclusive, do sistema físico que será controlado. Por exemplo: existe a possibilidade de utilizar um controlador lógico programável (o famoso CLP) para implementar o controlador PID de uma planta industrial e esta é, inclusive, uma das soluções mais utilizadas.
Dessa forma, a partir da próxima subseção, veremos mais detalhes, em uma visão geral, sobre como funcionam os controladores PID e, em seguida, para finalizar o tópico, analisaremos exemplos práticos desses controladores aplicados a sistemas de controle com os mais diversos tipos de sistemas reais. Vamos lá?
Visão Geral
Independentemente de como implementaremos o controlador PID, seja por meio de um controlador com outras funções, como é o caso de um controlador lógico programável, ou por meio de um circuito eletrônico analógico, um controlador PID é, por essência, formado com base em três tipos principais de ações em sua metodologia para controle do sistema: a proporcional, a integral e a derivativa. Estas podem, inclusive, ser utilizadas separadamente, o que nos gera ainda outros subtipos de controladores: os controladores P, de ação proporcional, os controladores PI (proporcional e integral) e os controladores PD (proporcional e derivativo).
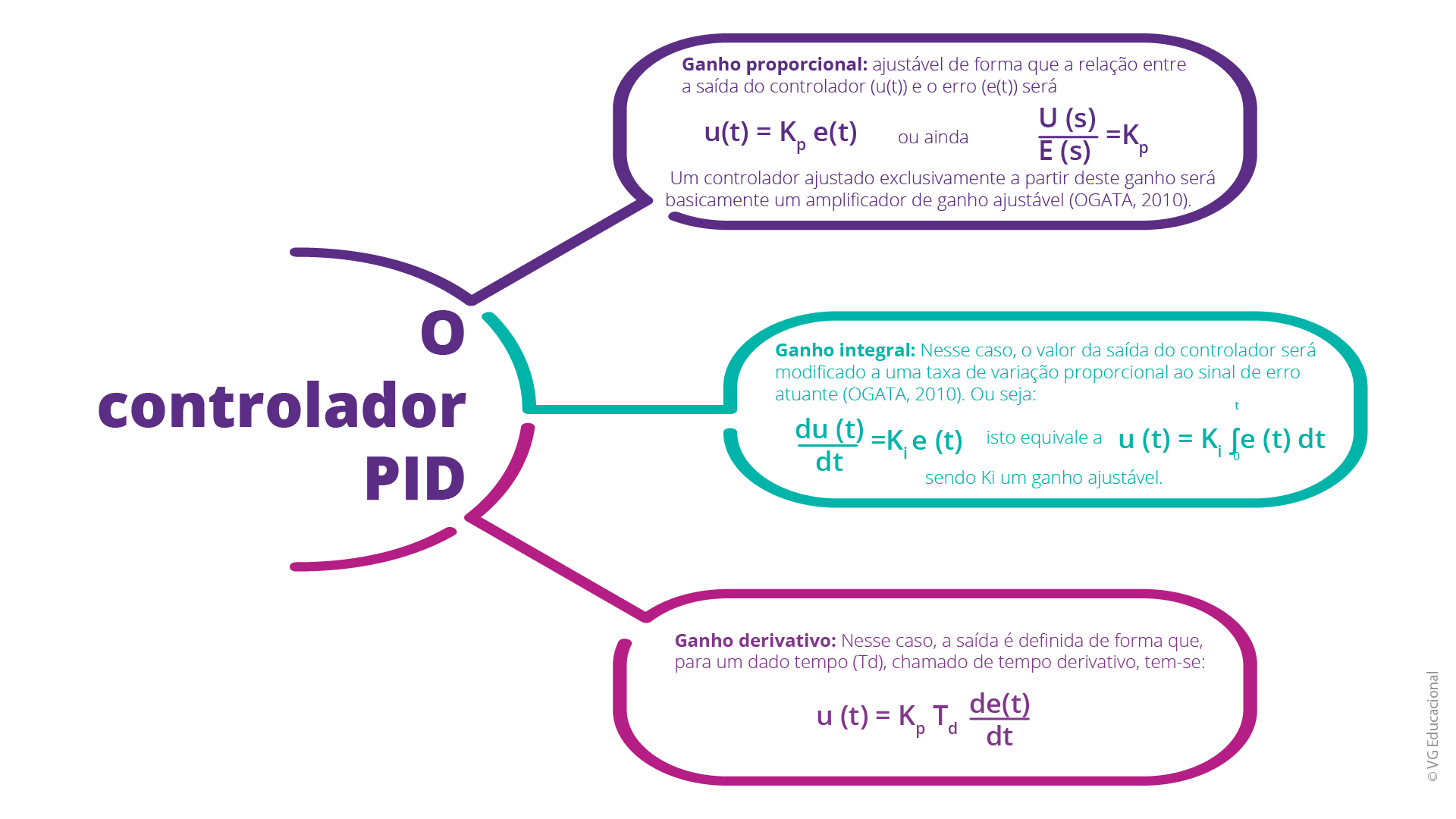
Fonte: VG Educacional
#PraCegoVer: o infográfico estático, intitulado “O controlador PID”, possui três caixas de texto interligados ao título, à direita. A primeira caixa de texto, intitulada “Ganho proporcional”, apresenta o texto “ajustável de forma que a relação entre a saída do controlador (u(t)) e o erro (e(t)) será \(u\left( t \right)~=~{{K}_{p}}e\left( t \right)\) (2) ou, ainda: \(\frac{U\left( s \right)}{E\left( s \right)}={{K}_{p}}\) (3). Um controlador ajustado exclusivamente a partir desse ganho será basicamente um amplificador de ganho ajustável (OGATA, 2010)”. A segunda caixa de texto, intitulada “Ganho integral”, apresenta o texto “nesse caso, o valor da saída do controlador será modificado a uma taxa de variação proporcional ao sinal de erro atuante (OGATA, 2010). Ou seja: \(\frac{du\left( t \right)}{dt}={{K}_{i}}e\left( t \right)\) (4). Isto equivale a: \(u\left( t \right)~=~{{K}_{i}}\mathop{\int }_{0}^{t}e\left( t \right)~dt\) (5), sendo Ki um ganho ajustável”. A terceira caixa de texto, intitulada “Ganho derivativo”, apresenta o texto “nesse caso, a saída é definida de forma que, para um dado tempo (Td), chamado de tempo derivativo, tem-se: \(u\left( t \right)~=~{{K}_{p}}{{T}_{d}}\frac{de\left( t \right)}{dt}\) (6)”.
Como mencionado, existirão então os controladores P, de ação proporcional, de forma que a saída será dada como apresentado pelas equações 2 e 3. Todavia, caso o controlador seja do tipo PI, a resposta será
\(u\left( t \right)~=~{{K}_{p}}e\left( t \right)+\frac{{{K}_{p}}}{{{T}_{i}}}\mathop{\int }_{0}^{t}e\left( t \right)dt\) (7)
o que gera a seguinte função de transferência ao controlador
\(\frac{U\left( s \right)}{E\left( s \right)}={{K}_{p}}\left( 1+\frac{1}{{{T}_{i}}s} \right)\) (8)
sendo Ti o tempo integrativo. Caso, por outro lado, tenhamos um controlador do tipo PD, sua resposta será
\(u\left( t \right)~=~{{K}_{p}}e\left( t \right)+{{K}_{p}}{{T}_{d}}\frac{de\left( t \right)}{dt}\) (9)
com a seguinte função de transferência:
\(\frac{U\left( s \right)}{E\left( s \right)}={{K}_{p}}\left( 1+{{T}_{d}}s \right)\) (10)
E o controlador PID? Bem, a resposta será, nesse caso, igual ao conjunto das ações, de maneira que se tem
\(u\left( t \right)~=~{{K}_{p}}e\left( t \right)+\frac{{{K}_{p}}}{{{T}_{i}}}\mathop{\int }_{0}^{t}e\left( t \right)dt+{{K}_{p}}{{T}_{d}}\frac{de\left( t \right)}{dt}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) (11)
e a seguinte função de transferência:
\(\frac{U\left( s \right)}{E\left( s \right)}={{K}_{p}}\left( 1+\frac{1}{{{T}_{i}}s}+{{T}_{d}}s \right)\) (12)
Perceba que, em todos os casos, o erro é considerado (diferença entre a saída do sistema e o que de fato se desejava para este) e, a partir de três estratégias distintas, decide-se como extingui-lo ou, ainda, ao menos atenuá-lo. Além disso, como você pode imaginar, em certos casos, considerar a amplificação do erro ou a taxa de variação deste ou sua integral, não será viável e, por esse motivo, utilizamos os controladores P, PI e PD.
Exemplos Práticos
Uma planta, independentemente do processo prático que esteja ocorrendo, pode ser controlada em malha fechada de forma que seu sistema estará estruturado, em realimentação, como apresentado no seguinte diagrama de blocos, considerando, ainda, a utilização de um controlador PID. O mesmo aconteceria para o uso de um controlador P, PI ou PD.
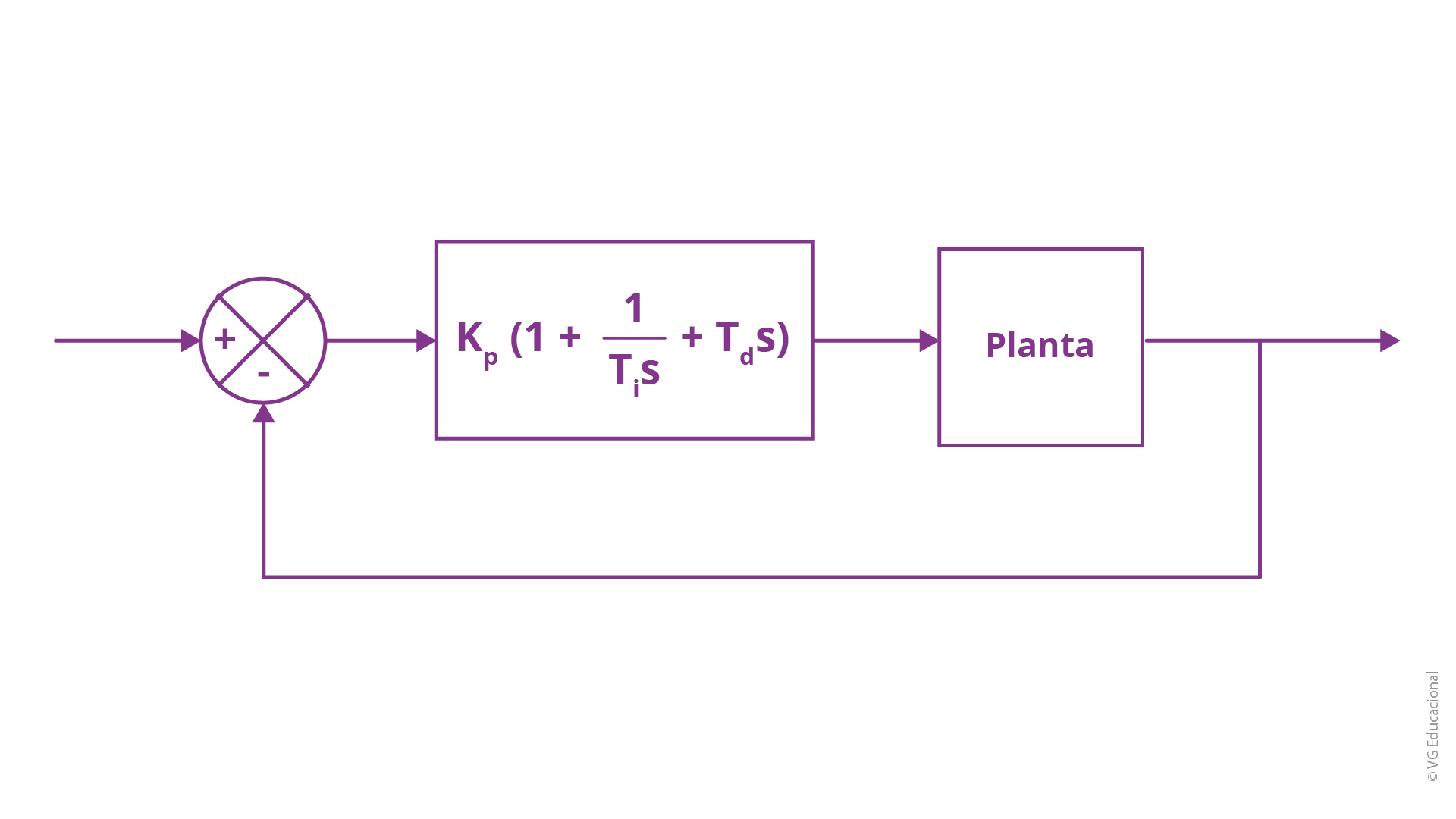
Fonte: Ogata (2010, p. 522).
#PraCegoVer: diagrama de blocos com a entrada conectada a um somador, seguida pelo bloco \({{K}_{p}}\left( 1+\frac{1}{{{T}_{i}}s}+{{T}_{d}}s \right)\) (Kp vezes 1 mais 1 sobre Ti vezes s, mais Td vezes s), em série com o bloco da planta, estando a saída conectada também ao somador, por uma realimentação unitária.
Além disso, a este ponto de estudo, na prática, é fundamental salientar que um controlador lógico programável poderá ser configurado de forma a atuar como um controlador P, PI, PD ou PID para essa planta. Por sua robustez e versatilidade, frente às outras necessidades de um sistema automatizado, essa é uma opção muito utilizada em sistemas industriais.
Um controlador PID, de ação proporcional, integral e derivativa, pode ser utilizado junto a uma dada planta industrial, visando à melhoria de sua resposta transitória e em regime permanente. Além disso, é importante observar que, em muitos casos, nem todas essas ações serão utilizadas para o controle do sistema.
Considerando essas informações, assinale a alternativa correta.
Bem, agora, a este ponto, você verá como fazemos, afinal, para ajustar os controladores PID, em busca de obter o melhor desempenho de um sistema de controle. Para isso, iniciaremos com uma visão geral sobre os métodos de sintonia clássicos, mais utilizados, além de abordarmos uma outra questão importante: o estudo de formas de mensurar o desempenho do sistema de controle. Por fim, encerraremos o estudo com exemplos práticos da utilização de métodos de sintonia. Vamos lá?
Visão Geral
Começando pelos métodos de Ziegler-Nichols, nesse caso, será sugerido escolher os valores para ajuste do controlador de acordo com parâmetros da resposta da planta ao degrau unitário, em um primeiro momento, de forma que utilizamos a seguinte tabela, com T sendo a constante de tempo e L, o atraso da resposta, para um dado valor de ganho do sistema, sendo sua função de transferência
\(G\left( s \right)~=~\frac{K{{e}^{-Ls}}}{Ts+1}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) (13)
e sua resposta gráfica, ao longo do tempo:
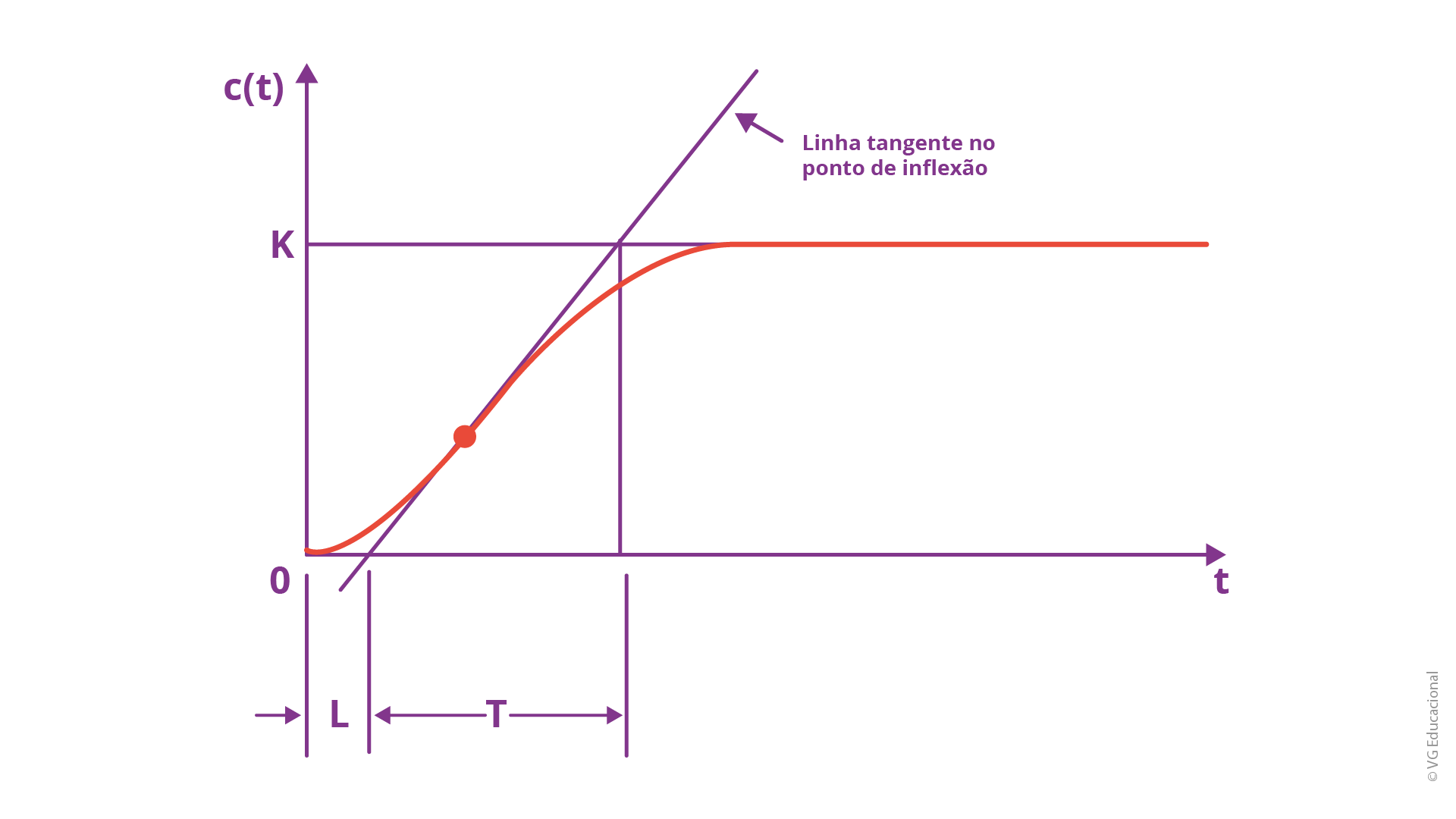
Fonte: Ogata (2010, p. 523).
#PraCegoVer: gráfico de t e c(t) (c t), com L correspondendo de 0 até o início da contabilização da constante de tempo T, que vai, por sua vez, até pouco antes de c(t) = K (c t igual a K), a partir da linha tangente no ponto de inflexão da curva de resposta.
O atraso e a constante de tempo são determinados a partir da reta tangente, traçada no ponto de inflexão da curva c(t), como visto no gráfico. Além disso, veja os ajustes sugeridos.
Fonte: Ogata (2010, p. 524).
#PraCegoVer: tabela com 4 linhas e 4 colunas. Na primeira linha, tem-se tipo do controlador, \({{K}_{p}}\), \({{T}_{i}}\) e \({{T}_{d}}\). Na segunda linha, tem-se P, T/L (T sobre L), \(\infty \) (infinito) e 0. Na terceira linha, tem-se PI, 0,9T/L (0,9 vezes T sobre L), L/0,3 (L sobre 0,3) e 0. Na quarta linha, tem-se 1,2T/L (1,2 vezes T sobre L), 2L (2 vezes L) e 0,5L (0,5 vezes L).
Em um segundo momento, o método de Ziegler-Nichols terá a opção de os ajustes se basearem em outros dois parâmetros: o ganho crítico (Kcr) e o período crítico (Pcr). O ganho crítico é obtido considerando o aumento de Kp até um dado valor em que o sistema apresenta oscilações sustentadas (ver no próximo gráfico), para controle do sistema sendo Ti ajustado em infinito e Td em zero:
Assim, utilizaremos a seguinte tabela para esse caso.
Fonte: Ogata (2010, p. 525).
#PraCegoVer: tabela com 4 linhas e 4 colunas. Na primeira linha, tem-se tipo de controlador, \({{K}_{p}}\), \({{T}_{i}}\) e \({{T}_{d}}\). Na segunda linha, tem-se P, \(0,5{{K}_{cr}}\) (0,5 vezes Kcr), \(\infty \) (infinito) e 0. Na terceira linha, tem-se PI, \(0,45{{K}_{cr}}\) (0,45 vezes Kcr), \({{P}_{cr}}/1,2\) (Pcr sobre 1,2) e 0. Na quarta linha, tem-se PID, \(0,6{{K}_{cr}}\) (0,6 vezes Kcr), \(0,5{{P}_{cr}}\) (0,5 vezes Pcr) e \(0,125{{P}_{cr}}\) (0,125 vezes Pcr).
Uma outra possibilidade para a sintonia do controlador PID é o método CHR (Chien, Hrone e Reswick), desenvolvido em 1952 como uma possível alternativa para resolver problemas vistos a partir da resposta ao degrau, capaz de auxiliar no aumento da estabilidade do sistema (DORF, 2018).
Nesse sentido, consideraremos dois critérios como base para a sintonia, qual a resposta mais rápida possível sem sobrevalor e qual poderia ser esta, considerando 20% de sobressinal, atendendo a tipos de situações práticas como a presença de perturbação de carga, em sistemas de regulação e servo rastreamento.
Sem o sobressinal, fazemos o ajuste conforme a próxima tabela, caso tenhamos o sistema servo.
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 4 linhas e 4 colunas. Na primeira linha, tem-se tipo de controlador, \({{K}_{p}}\), \({{T}_{i}}\) e \({{T}_{d}}\). Na segunda linha, tem-se P, 0,3T/K.L (0,3 vezes T sobre K vezes L), \(\infty \) (infinito) e 0. Na terceira linha, tem-se PI, 0,35T/K.L (0,35 vezes T sobre K vezes L), 1,16T (1,16 vezes T) e 0. Na quarta linha, tem-se PID, 0,6T/K.L (0,6 vezes T sobre K vezes L), T e L/2 (L sobre 2).
Considerando, por outro lado, 20% de sobressinal, teremos o seguinte:
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 4 linhas e 4 colunas. Na primeira linha, tem-se tipo de controlador, \({{K}_{p}}\), \({{T}_{i}}\) e \({{T}_{d}}\). Na segunda linha, tem-se P, 0,7T/K.L (0,7 vezes T sobre K vezes L), \(\infty \) (infinito) e 0. Na terceira linha, tem-se PI, 0,6T/K.L (0,6 vezes T sobre K vezes L), T e 0. Na quarta linha, tem-se PID, 0,95T/K.L (0,95 vezes T sobre K vezes L), 1,357T (1,357 vezes T) e 0,437L (0,437 vezes L).
Caso tenhamos ainda outro tipo de sistema, como um sistema regulador, algumas pequenas mudanças são feitas do ponto de vista numérico, mas os mesmos tipos de parâmetros devem ser considerados. O método CC, também conhecido como método Cohen-Coon, foi estabelecido no ano de 1953, por sua vez, e pretende atender ajustes para o controlador PID em casos e para sistemas do tipo da Equação 13. A tabela a ser seguida para ajuste, neste caso, é:
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 4 linhas e 4 colunas, sendo, na primeira linha, tipo de controlador, \({{K}_{p}}\), \({{T}_{i}}\) e \({{T}_{d}}\). Na segunda linha, P, \(\left( 1,03+0,35\left( \frac{L}{T} \right) \right)\frac{T}{K.L}\) (1,03 mais 0,35 vezes L sobre T, vezes T sobre K vezes L, \(\infty \) (infinito) e 0. Na terceira linha PI, \(\left( 0,9+0,083\left( \frac{L}{T} \right) \right)\frac{T}{K.L}\) (0,9 mais 0,083 vezes L sobre T, vezes T sobre K vezes L), \(\left( \frac{0,9+0,083\left( \frac{L}{T} \right)}{1,27+0,6\left( \frac{L}{T} \right)} \right)L\) (0,9 mais 0,083 vezes L sobre T, sobre 1,27 mais 0,6 vezes L sobre T, vezes L e 0. Na quarta linha PID, \(\left( 1,35+0,25\left( \frac{L}{T} \right) \right)\frac{T}{K.L}\) (1,35 mais 0,25 vezes L sobre T, vezes T sobre K vezes L, \(\left( \frac{1,35+0,25\left( \frac{L}{T} \right)}{0,54+0,33\left( \frac{L}{T} \right)} \right)L\) (1,35 mais 0,25 vezes L sobre T, sobre 0,54 mais 0,33 vezes L sobre T, vezes L) e \(\left( \frac{0,5L}{1,35+0,25\left( \frac{L}{T} \right)} \right)\) (0,5 vezes L, sobre 1,35 mais 0,25 vezes L sobre T).
Por fim, com relação aos métodos de sintonia, podemos citar ainda o IMC, Internal Model Control (Modelo de Controle Interno), que é estabelecido a partir do modelo matemático do sistema a ser controlado, gerado pela curva de reação, após a aplicação de um degrau na entrada deste sistema estabelecido em malha aberta e, juntamente a uma especificação de desempenho. Supondo que a função de transferência desejada seja
\[{{G}_{desejada}}\left( s \right)~=~\frac{1}{\lambda s+1}\]
em que \(\lambda \) é um parâmetro de projeto do sistema, a ser escolhido de acordo com a dinâmica deste. A tabela para ajustes do controlador, a ser utilizada no método, é apresentada a seguir, de acordo com o modelo do sistema.
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 6 linhas e 4 colunas. Na primeira linha, tem-se modelo do processo, \({{K}_{p}}\), \({{T}_{i}}\) e \({{T}_{d}}\). Na segunda linha, tem-se \(\frac{K}{\tau s+1}\) (K sobre tau vezes s mais 1), \(\frac{\tau }{K\lambda }\) ()tau sobre K vezes lambda), \(\tau \) (tau) e 0. Na terceira linha, tem-se \(\frac{K}{\left( {{\tau }_{1}}s+1 \right)\left( {{\tau }_{2}}s+1 \right)}\) (K sobre tau 1 vezes s mais 1, vezes tau 2 vezes s mais 1), \(\frac{\left( {{\tau }_{1}}+{{\tau }_{2}} \right)}{K\lambda }\) (tau 1 mais tau 2, sobre K vezes lambda), \({{\tau }_{1}}+{{\tau }_{2}}\) (tau 1 mais tau 2) e \(\frac{{{\tau }_{1}}{{\tau }_{2}}}{{{\tau }_{1}}+{{\tau }_{2}}}\) (tau 1 vezes tau 2, sobre tau 1 mais tau 2). Na quarta linha, tem-se \(\frac{K}{{{\tau }^{2}}{{s}^{2}}+2\varsigma \tau s+1}\) (K sobre tau ao quadrado vezes s ao quadrado, mais 2 vezes csi vezes tau vezes s, mais 1), \(\frac{2\varsigma \tau }{K\lambda }\) (2 vezes csi vezes tau, sobre K vezes lambda), \(2\varsigma \tau \) (2 vezes csi vezes tau) e \(\frac{\tau }{2\varsigma }\) (tau sobre duas vezes csi). Na quinta linha, tem-se K/s (K sobre s), \(\frac{1}{K\lambda }\) (1 sobre K vezes lambda), \(\infty \) (infinito) e 0. Na sexta linha, tem-se \(\frac{K}{s\left( \tau s+1 \right)}\), \(\frac{1}{K\lambda }\) (1 sobre K vezes lambda), 0 e \(\tau \) (tau).
Já com relação à avaliação de desempenho dos controladores PID, podemos ressaltar alguns indicadores. O IAE (Integral de Erro Absoluto) é um exemplo desses indicadores e pode ser calculado como,
\(IAE~=~\mathop{\int }_{0}^{\infty }E\left( t \right)~dt~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) (14)
sendo E(t) o erro absoluto como função do tempo (FRANCHI, 2011). Outro indicador também frequente é o ITAE (Integral do Erro Ponderado no Tempo), que pode ser calculado como:
\(ITAE~=~\mathop{\int }_{0}^{\infty }E\left( t \right).t~~dt~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) (15)
Por fim, o Erro Quadrático Médio (ISE - Integral Square Error) é definido como
\(ISE~=~\mathop{\int }_{0}^{\infty }{{E}^{2}}\left( t \right)~dt~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) (16)
e também servirá para avaliação do desempenho de um dado controlador PID. A seguir, finalizaremos nossos estudos, neste material, visualizando o ajuste de um controlador PID na prática.
Exemplos Práticos
Vamos considerar agora, por fim, o projeto de um sistema de controle do início ao fim, na prática, escolhendo como método de sintonia, o método de Ziegler-Nichols. Veja o sistema, a seguir, com a representação, inclusive, da função de transferência da planta.
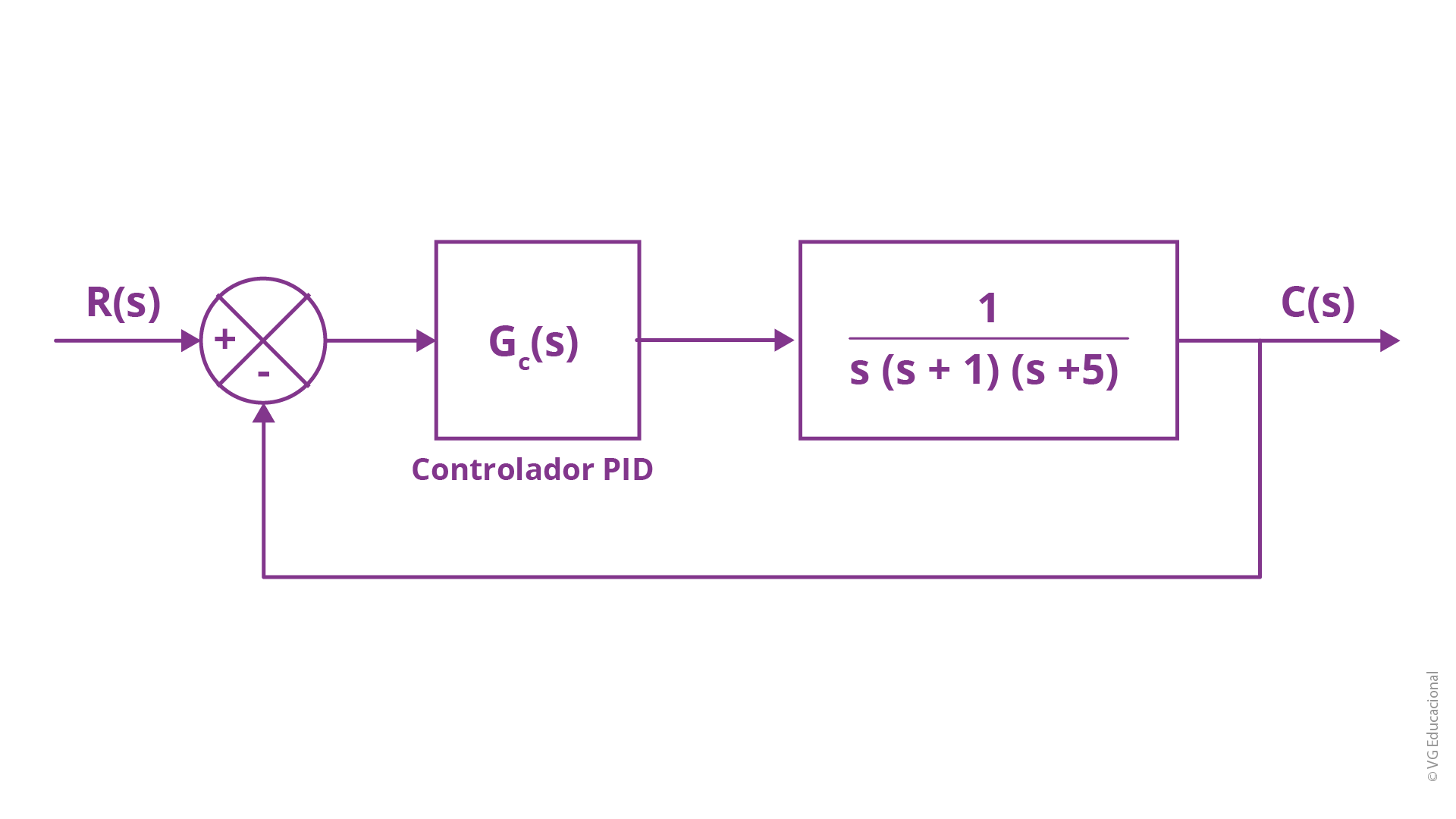
Fonte: Ogata (2010, p. 526).
#PraCegoVer: diagrama de blocos com R(s) (r s) de entrada, um somador, em seguida o bloco do controlador PID (Gc(s)) (Gc s), o bloco da planta, 1/s(s+1)(s+5) (1 sobre s vezes s mais 1 vezes s mais 5), a saída C(s) (c s), que está conectada em realimentação unitária com o somador.
O primeiro passo é, a partir da escolha do método de sintonia, entender características que possam nos orientar a ter êxito mais rapidamente no projeto do sistema de controle. Perceba que há o fator 1/s, um integrador e, assim, isso pode ser um indicador para utilizarmos o segundo método de Ziegler-Nichols. Assim, partimos fazendo Ti = 0 e Td = 0, com a seguinte função de transferência em malha fechada sendo nossa referência,
\[G\left( s \right)~=~\frac{C\left( s \right)}{R\left( s \right)}=\frac{{{K}_{p}}}{s\left( s+1 \right)\left( s+5 \right)+{{K}_{p}}}=\frac{{{K}_{p}}}{{{s}^{3}}+6{{s}^{2}}+5s+{{K}_{p}}}\]
e, assim, obtemos a seguinte tabela de Routh para entender a estabilidade e, em seguida, projetar o controlador.
Fonte: Elaborada pela autora.
#PraCegoVer: tabela com 4 linhas e 3 colunas. Na primeira linha, tem-se s³ (s elevado ao cubo), 1 e 5. Na segunda linha, tem-se s² (s elevado ao quadrado), 6 e \({{K}_{p}}\). Na terceira linha, tem-se s¹ (s elevado a 1), \(\left( 30-{{K}_{p}} \right)/6\) (30 menos \({{K}_{p}}\) sobre 6) e na quarta \({{s}_{0}}\) (s elevado a 0) e \({{K}_{p}}\).
Vendo a primeira coluna da tabela, as oscilações sustentadas ocorrem a um ganho Kp = 30, o que nos permite concluir que Kcr = 30. Assim, a função de transferência torna-se:
\[G\left( s \right)~=~\frac{30}{{{s}^{3}}+6{{s}^{2}}+5s+30}\]
Para encontrar o período das oscilações (Pcr), fazemos:
\[{{(j\omega )}^{3}}+6{{(j\omega )}^{2}}+5\left( j\omega \right)+30~=~0\]
\[{{\omega }^{2}}=5~\to ~\omega =\sqrt{5} \Rightarrow {{P}_{cr}}=\frac{2\pi }{\omega }=2,809\]
Logo, os ajustes para o controlador PID serão, neste caso:
\[{{K}_{p}}=0,6{{K}_{cr}}=18;~{{T}_{i}}=0,5{{P}_{cr}}=1,405;~{{T}_{d}}=0,125{{P}_{cr}}=0,351\]
Assim, a função de transferência do controlador é:
\[{{G}_{c}}\left( s \right)~=~{{K}_{p}}\left( 1+\frac{1}{{{T}_{i}}s}+{{T}_{d}}s \right)=18\left( 1+\frac{1}{1,405s}+0,351s \right)=\frac{6,322\left( s+1,423 \right){}^\text{2}}{s}\]
lembrando que, por conveniência, podemos representar essa função no bloco do controlador, tornando mais claro, assim, o processo de simulação do sistema de controle. Caso a resposta ao degrau unitário não seja satisfatória, considerando um sobressinal máximo de 20%, por exemplo, outro método pode ser utilizado ou podemos, também, fazer um ajuste fino dos parâmetros do controlador PID.
Suponha que obtivéssemos a resposta unitária do sistema de controle obtido anteriormente e chegássemos à conclusão de que é necessário melhorar o sistema de controle, de maneira a gerar uma resposta com menor sobressinal, por exemplo.
Qual seria sua estratégia nesse caso?
O conhecimento e a experiência do profissional responsável pelo desenvolvimento do sistema de controle podem auxiliar muito nesses casos, permitindo, em um primeiro momento, optar por fazer alguns ajustes finos nos parâmetros já obtidos pelo método (nesse caso, o segundo método de Ziegler-Nichols). Todavia, caso o resultado ainda não fosse satisfatório, uma boa opção seria utilizar o modelo matemático do sistema a ser controlado, como base, utilizando o método IMC.
Critério de estabilidade de Routh (ELT009, ELT035)
Canal: Luis Antônio Aguirre
Comentário: Nesta videoaula, é apresentado o critério de estabilidade de Routh, a partir da construção do arranjo de Routh, sem explicar a matemática que suporta esse método, visto no Tópico 2.1 deste material, juntamente com dois exemplos de aplicação.
Disponível em:

Controle automático
Autores: Plínio de Lauro Castrucci; Anselmo Bittar; Roberto Moura Sales
Editora: LTC
Capítulo: 7
Ano: 2018
ISBN: 9788521635611
Comentário: Neste livro, especialmente no capítulo 7, são apresentadas várias estratégias, incluindo o uso do controlador PID, direcionadas ao controle de processos industriais. Assim, com essa leitura, você aprenderá alguns aspectos gerais que, normalmente, são considerados, bem como questões específicas de alguns processos a partir de exemplos práticos.
Fonte: Disponível na Biblioteca Virtual.
Bem, tivemos a oportunidade de entender, afinal, o que significa um sistema ser estável, marginalmente estável ou instável, e quais são as implicações práticas. Além disso, vimos como aplicar as ferramentas e os recursos matemáticos mais utilizados nesses tipos de análises, que podem preceder, por exemplo, o projeto do sistema de controle. Também podemos perceber, ao longo desta unidade, o quanto a simulação de sistemas dinâmicos já faz parte da realidade, em muitas situações práticas, e como essas ações podem facilitar o desenvolvimento do sistema de controle. Por falar nesse último, vimos o quanto os controladores PID são frequentes em sistemas de controle industriais bem como estratégias para sintonizá-los.
Espero que você tenha conseguido conectar-se com a prática, ao longo do conteúdo estudado, pois questões como o entendimento da estabilidade de um sistema a ser controlado ou já controlado bem como os recursos matemáticos utilizados, com frequência, para a obtenção de um efetivo controlador para um dado processo ou planta, serão fundamentais para que você obtenha êxito em muitas situações práticas. Até uma próxima oportunidade!
CASTRUCCI, P. de L.; BITTAR, A.; SALES, R. M. Controle automático. Rio de Janeiro: LTC, 2018.
CONTROL systems. Scilab, [2020]. Disponível em: https://www.scilab.org/software/xcos/control-systems. Acesso em: 28 mar. 2022.
CONTROL system toolbox. Mathworks, [2022]. Disponível em: https://www.mathworks.com/products/control.htm. Acesso em: 28 mar. 2022.
CRITÉRIO de Estabilidade de Routh (ELT009, ELT035). [S. l.: s. n.], 2018. 1 vídeo (14 min.). Publicado pelo canal Luis Antonio Aguirre. Disponível em: https://www.youtube.com/watch?v=NjyjJ6qtOMs. Acesso em: 29 mar. 2022.
DORF, R. C. Sistemas de controle moderno. 13. ed. Rio de Janeiro: LTC, 2018.
FRANCHI, C. M. Controle de processos industriais: princípios e aplicações. São Paulo: Editora Érica, 2011.
NISE, N. S. Engenharia de sistemas de controle. 7. ed. Rio de Janeiro: LTC, 2017.
OGATA, K. Engenharia de controle moderno. 5. ed. São Paulo: Pearson Prentice Hall, 2010.
SIMULAÇÃO de tanque (ELT009, ELT035, ELT016). [S. l.: s. n.], 2017. 1 vídeo (18 min.). Publicado pelo canal Luis Antonio Aguirre. Disponível em: https://www.youtube.com/watch?v=JUSfsLFt8tc. Acesso em: 29 mar. 2022.