Controle de Sistemas
Sistemas de Controle, Método do Lugar Geométrico das Raízes e Diagrama de Bode
Tempo de leitura do conteúdo estimado em 1 hora e 30 minutos.
Olá, estudante! Iniciaremos nossos estudos discorrendo sobre o projeto de controladores PID (proporcional, integral e derivativo) — que pode ser realizado, de maneira facilitada, a partir de diversos tipos de abordagens. Entre esses enfoques, podemos destacar o método do Lugar Geométrico das Raízes (LGR), uma das possíveis formas de representação de sistemas de controle, com polos e zeros, além do Diagrama de Bode, outra importante ferramenta para a representação da resposta no domínio da frequência de um dado sistema. Nesse sentido, estudaremos, inicialmente, a partir de uma visão geral e, a título de exemplificação, analisaremos alguns exemplos práticos do método do Lugar Geométrico das Raízes. Essa técnica pode ser utilizada na representação de um sistema real, pois é utilizada para o desenvolvimento do projeto de um controlador PID. Por fim, encerraremos esse material de estudo aprofundando nossos conhecimentos através do desenvolvimento do Diagrama de Bode e suas possibilidades de utilização na prática, além da sua utilização no projeto de um controlador PID, enfatizando sobre o papel dos software e dos algoritmos nesse tipo de técnica.
Bons estudos!
Você sabia que o lugar geométrico das raízes é uma possibilidade usual na representação gráfica de um sistema de controle, mais precisamente dos polos em malha fechada, considerando a variação de um dos parâmetros deste sistema? Com isto, torna-se viável o projeto de um sistema de controle, permitindo, também, analisar a estabilidade e a resposta transitória do sistema controlado. Com base nessas informações, começaremos nossa análise a partir da familiarização com a representação para, em seguida, analisarmos, através de exemplos práticos, como é obtido o esboço à mão e o delineamento computacional do processo.
Visão Geral
A representação gráfica da técnica do Lugar Geométrico das Raízes utiliza, como base, a representação vetorial de números complexos. Nesse sentido, precisamos saber a distância dos polos e a distância dos zeros, bem como os ângulos formados. Além disso, cabe a utilização de software para a obtenção facilitada dessas representações. Falaremos mais sobre esse assunto adiante.
O lugar geométrico das raízes pode ser obtido por meio de uma varredura no plano s, cuja soma dos ângulos resultam em um múltiplo ímpar de 180°. Posteriormente, à mão, é feito um esboço um pouco mais simplificado para facilitar a compreensão. A utilização de assíntotas pode ser significativamente facilitadora nesse processo.
Representação pelo método do Lugar Geométrico das Raízes
Correspondente ao número de polos em malha fechada.
O lugar geométrico das raízes é simétrico em relação ao eixo real.
Para K > 0, o lugar geométrico das raízes existe à esquerda de um número ímpar de polos e/ou zeros em malha aberta, no eixo real.
Início nos polos finitos e infinitos de G(s)H(s) e término nos zeros finitos e infinitos de G(s)H(s).
O lugar geométrico das raízes tende às assíntotas quando tender ao infinito. As equações dessas retas são dadas pela interseção com o eixo real e os ângulos formados, que em radianos são calculados como:
#PraCegoVer: o infográfico interativo, intitulado “Representação pelo método do Lugar Geométrico das Raízes”, possui cinco botões interativos, alinhados verticalmente. O primeiro botão interativo, intitulado “Número de ramos”, ao ser clicado, apresenta o texto “correspondente ao número de polos em malha fechada”. O segundo botão interativo, intitulado “Simetria”, ao ser clicado, apresenta o texto “o lugar geométrico das raízes é simétrico em relação ao eixo real”. O terceiro botão interativo, intitulado “Segmentos do eixo real”, ao ser clicado, apresenta o texto “para K > 0, o lugar geométrico das raízes existe à esquerda de um número ímpar de polos e/ou zeros em malha aberta, no eixo real”. O quarto botão interativo, intitulado “Pontos de início e término”, ao ser clicado, apresenta o texto “início nos polos finitos e infinitos de G(s)H(s) e término nos zeros finitos e infinitos de G(s)H(s)”. O quinto botão interativo, intitulado “Comportamento no infinito”, ao ser clicado, apresenta o texto “o lugar geométrico das raízes tende às assíntotas quando tender ao infinito. As equações dessas retas são dadas pela interseção com o eixo real e os ângulos formados, que em radianos são calculados como: \({{\phi }_{a}}=\frac{\mathop{\sum }_{{}}^{{}}polos~finitos~-~\mathop{\sum }_{{}}^{{}}zeros~finitos}{\#polos~finitos~-~\#zeros~finitos}\); \({{\theta }_{a}}=\frac{\left( 2k+1 \right)\pi }{\#polos~finitos~-~\#zeros~finitos}\)”.
Como regras adicionais, que podem ser utilizadas para o refinamento do esboço, devemos ter atenção aos pontos de entrada e de saída do eixo real. Vale a pena lembrar que o lugar das raízes sai do eixo real em um ponto — ganho máximo, e retorna nesse mesmo eixo — ganho mínimo. Podem ser calculados, com maior precisão, os cruzamentos no eixo imaginário a partir da informação de fase.
\[/ \text{_} G\left( s \right)H\left( s \right)=\left( 2k+1 \right)180{}^\circ \]
Por fim, deve-se considerar os ângulos de partida e de chegada. Sendo assim, o ganho K será dado por:
\[K=\frac{1}{\left| G\left( s \right)H\left( s \right) \right|}=\frac{1}{M}=\frac{\mathop{\prod }_{{}}^{{}}dist\hat{a}ncias~at\acute{e}~os~polos~finitos}{\mathop{\prod }_{{}}^{{}}dist\hat{a}ncias~at\acute{e}~os~zeros~finitos}\]
Exemplos
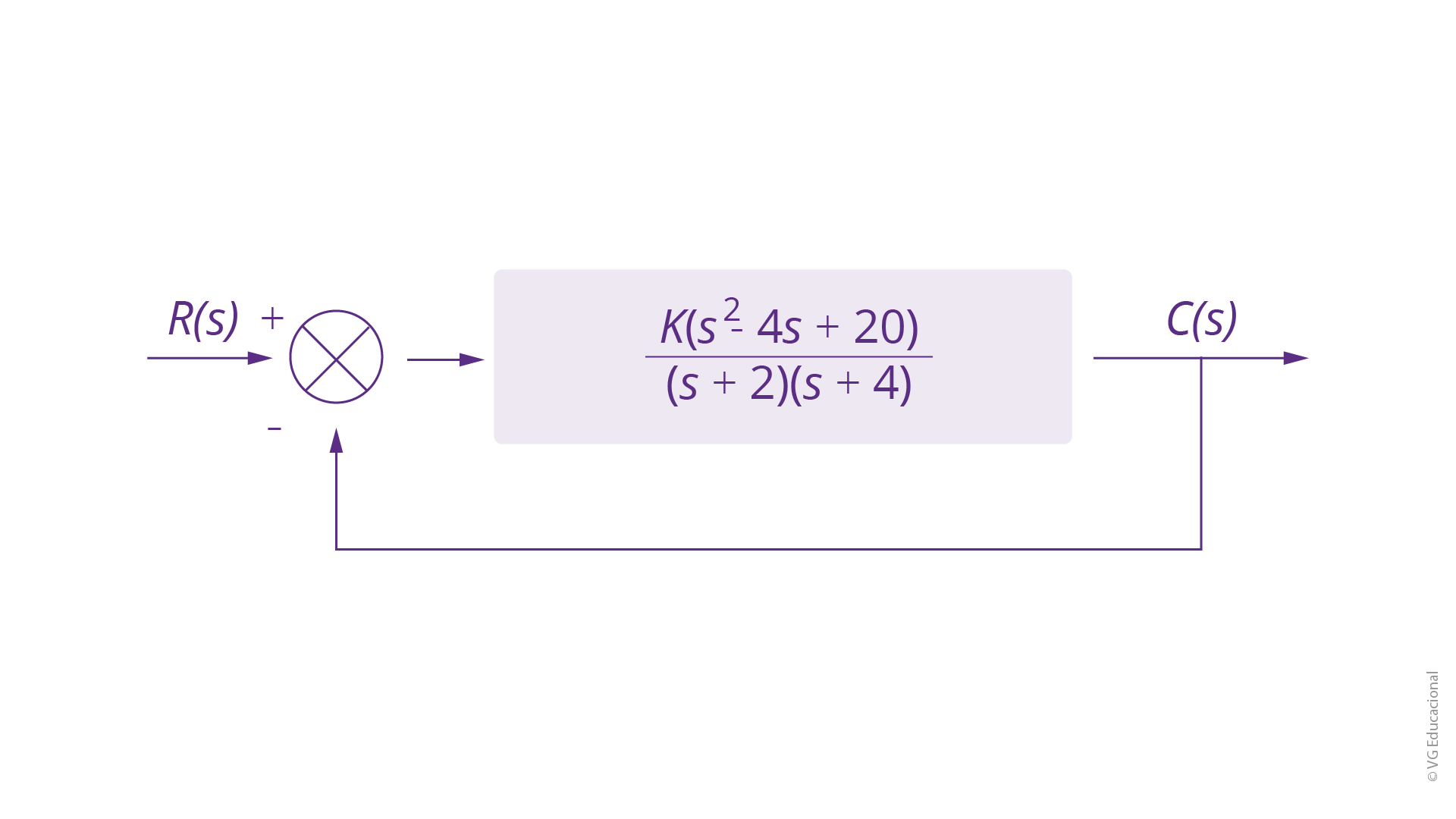
Agora, considere a obtenção do lugar geométrico das raízes no sistema prático a seguir.
Para o sistema, o segmento do eixo real será determinado de acordo com os polos, entre -2 e -4. Em seguida, devemos nos lembrar que o lugar geométrico das raízes inicia nos polos de malha aberta e encerra nos zeros da malha fechada. Com isso, temos o seguinte esboço:
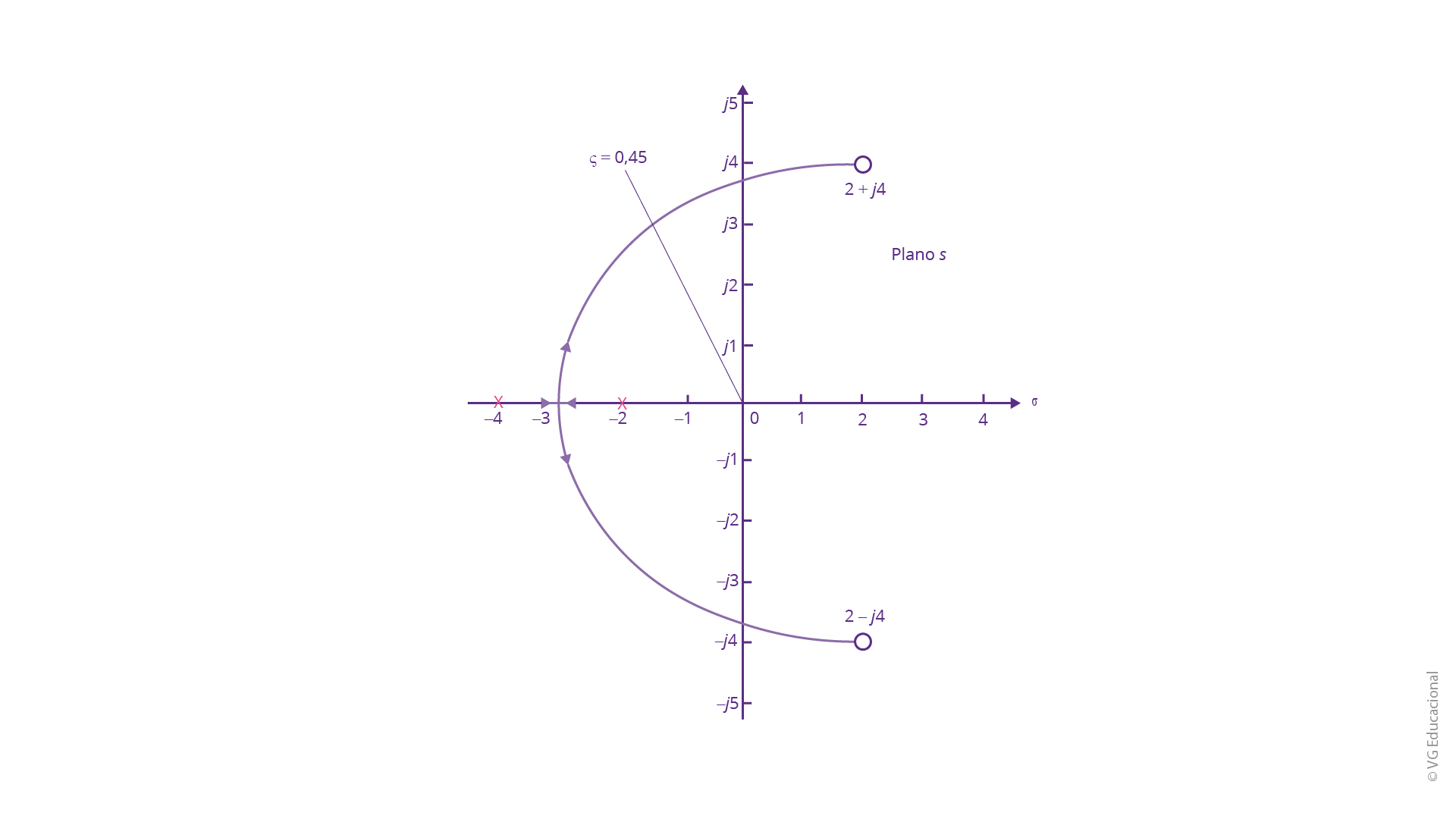
Fonte: Nise (2018, p. 612).
#PraCegoVer: o plano s com o eixo real \(\sigma \) e o eixo imaginário \(j\omega \). Em seguida, são marcados os pontos 2 + j4 e 2 - j4 e, posteriormente, desenha-se um semicírculo entre eles. Além disso, são marcados, com um X, os pontos -4 e -2 no eixo real, e tem-se a reta partindo da origem \(\varsigma =0,45\).
Como exemplificação, suponhamos que haja a necessidade de saber qual o ponto exato em que o lugar geométrico das raízes cruza a reta estabelecida, sendo o amortecimento 0,45. Para isso, é possível desenvolver o processo de procura computacionalmente, mas o ângulo nesse caso será:
\[\theta =180{}^\circ -co{{s}^{-1}}0,45=116,7{}^\circ \]
Através das coordenadas polares, percebemos que o ponto será: 3,4/_116,7°, com ganho de 0,417. Já para saber a faixa em que o sistema é estável, podemos considerar \(\theta =90{}^\circ \), ponto no qual os ângulos totalizam um múltiplo ímpar de 180°. Todavia, ao buscarmos através das coordenadas polares, percebemos que o lugar geométrico das raízes cruza o eixo imaginário, com um ganho de K = 1,5. Nesse tipo de situação, é interessante termos o auxílio de um software, pois auxiliará no projeto do sistema de controle, tornando possível sua conclusão. Vale lembrar, também, que o ganho K pode ser ajustado entre 0 e 1,5.
O processo de obtenção do lugar geométrico das raízes é relativamente simples por meio computacional. Via software MATLAB, por exemplo, pode ser feito de forma muito fácil. Considerando a seguinte função de transferência, temos:
\[G\left( s \right)~=~\frac{2{{s}^{2}}+5s+1}{{{s}^{2}}+2s+3}\]
Nesse caso, poderíamos dar os seguintes comandos: sys = tf([2 5 1],[1 2 3]); rlocus(sys). O gráfico seria gerado e, além disso, tornaria possível obter o vetor de ganhos da malha fechada e a localização das raízes complexas, como saída desta última função.
REFLITA
Um sistema estável, instável ou marginalmente estável possuirá representações características obtidas através do método do lugar geométrico das raízes. Desta forma, você consegue imaginar como poderíamos trazer certas características para o sistema físico real, representado através deste método, auxiliando, assim, no projeto de um sistema de controle? Dica: podemos estabelecer condições, em alguns casos possíveis, para obtê-lo na prática a partir da localização dos polos e dos zeros, tornando o sistema estável.
A seguir, veja como é possível utilizar a representação através do método do lugar geométrico das raízes para o projeto de um controlador P, PI, PD ou PID, atendendo às diversas especificações de projeto.
O lugar geométrico das raízes pode ser compreendido, basicamente, como o percurso realizado pelas raízes da equação característica, traçado através do plano s, considerando a variação de um dado parâmetro, como um ganho K, por exemplo.
A partir dessa informação, é correto afirmar que:
Agora, caro(a) estudante, veremos como empregar esta importante metodologia de representação na prática, aplicando os conhecimentos, até aqui adquiridos, para a elaboração do projeto de um sistema de controle. Iniciaremos com uma visão geral e, depois, apresentarei o passo a passo através de exemplos práticos. Vamos lá?
Visão Geral
O projeto de um sistema de controle, no contexto da utilização do método do lugar geométrico das raízes, poderá atender a questões específicas, como a escolha de um dado ganho adequado, considerando a especificação estabelecida para a resposta transitória do sistema, por exemplo. Todavia, devemos nos atentar para o estabelecimento de um sistema de controle que, nesse caso, estará limitado às respostas obtidas ao longo do lugar geométrico das raízes em questão. Isto ficará mais claro ao longo dos nossos estudos.
Para visualizar como se configura o avanço, suponhamos um polo, um zero e um ponto qualquer no plano complexo. Por meio da configuração dos ângulos, em que há um ângulo positivo resultante das diferenças entre eles, teremos, por consequência, um avanço de fase. Vejamos, na figura abaixo, como ficou a representação do polo e do zero do compensador através da situação descrita anteriormente.
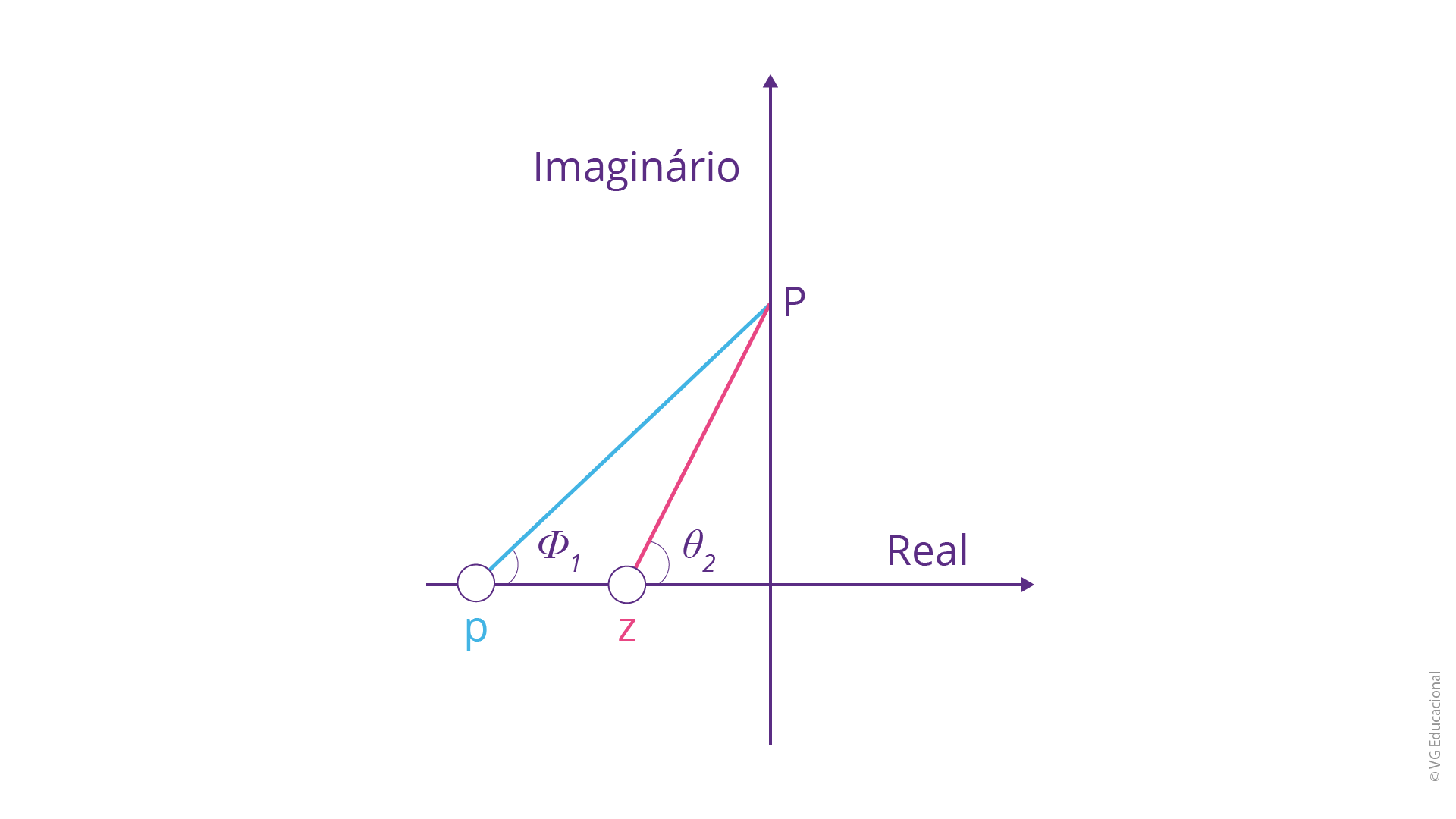
Fonte: Elaborada pelo autor.
#PraCegoVer: representação no plano s, com o eixo x sendo o real e o eixo y o imaginário. O polo possui menor magnitude e está localizado sobre o eixo real, com o zero localizado um pouco mais à frente, nesse mesmo eixo. O polo faz um ângulo de \({{\phi }_{1}}\) para a projeção no ponto P, no eixo imaginário, e o zero o ângulo \({{\theta }_{1}}\), mais aberto, para a projeção nesse mesmo ponto.
Considera-se o desenvolvimento do projeto dada a especificação de um determinado ponto desejável para o polo do sistema. Geralmente, escolhemos, de forma arbitrária, o polo ou o zero e determinamos, a partir disso, a contribuição angular deste ponto, junto aos pontos já existentes de malha aberta — polo(s) e zero(s) do sistema controlado.
Levando em conta um compensador em atraso, o contrário irá acontecer. Esse tipo de controlador, pelo fato do módulo zero, neste caso, ser maior que o do polo, poderá, ainda, ser representado e compreendido. Além disso, possui um funcionamento semelhante a um circuito passa-baixa. O processo de compensação, nesse caso em específico, proporcionará efeitos positivos em regime permanente, embora ocorra, em alguns casos, um frequente aumento no tempo de estabilização do sistema. Vejamos, agora, o lugar geométrico das raízes, considerando a presença ou não da compensação por atraso de fase.
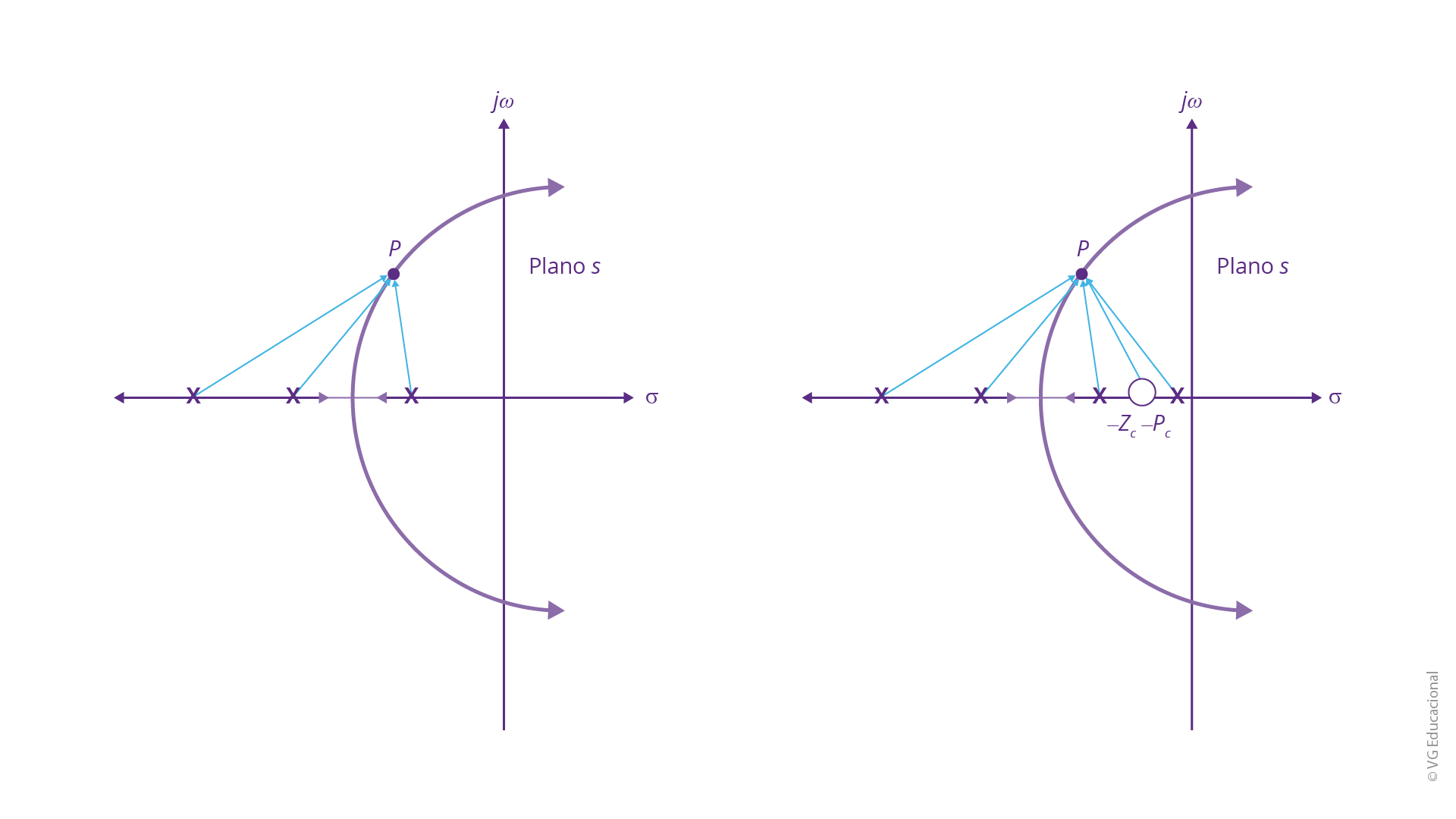
Fonte: Nise (2018, p. 689).
#PraCegoVer: do lado esquerdo, tem-se o plano s, com o eixo real \(\sigma \) e o eixo imaginário \(j\omega \). Esse plano é representado por três pontos no eixo real, marcados com x. Em seguida, é traçado um semicírculo, que cruza o eixo real entre o segundo e o terceiro ponto marcado e com as setas saindo desses pontos, convergindo para um ponto P no semicírculo. Do lado direito, tem-se o plano s, com o eixo real \(\sigma \) e o eixo imaginário \(j\omega \). Esse plano é representado por três pontos no eixo real, marcados com x. Em seguida, é traçado um semicírculo, que cruza o eixo real entre o segundo e o terceiro ponto marcado e com setas saindo desses pontos, convergindo para um ponto P no semicírculo. Além disso, ainda nesse mesmo plano, tem-se, agora, outros dois pontos mais à frente: o primeiro marcado com uma bola, denominado -zc e o segundo, com outro x, denominado -pc, também com retas apontando para o ponto P.
Por fim, temos o compensador em avanço e em atraso de fase, que atua combinando as duas ações (de avanço e de atraso de fase), objetivando o controle do sistema. A função de transferência será:
\[{{G}_{c}}\left( s \right)={{K}_{c}}\frac{\left( s+{{z}_{1}} \right)}{\left( s+{{p}_{1}} \right)}\frac{\left( s+{{z}_{2}} \right)}{\left( s+{{p}_{2}} \right)}\]
Logo, o compensador poderá ser representado da seguinte forma:
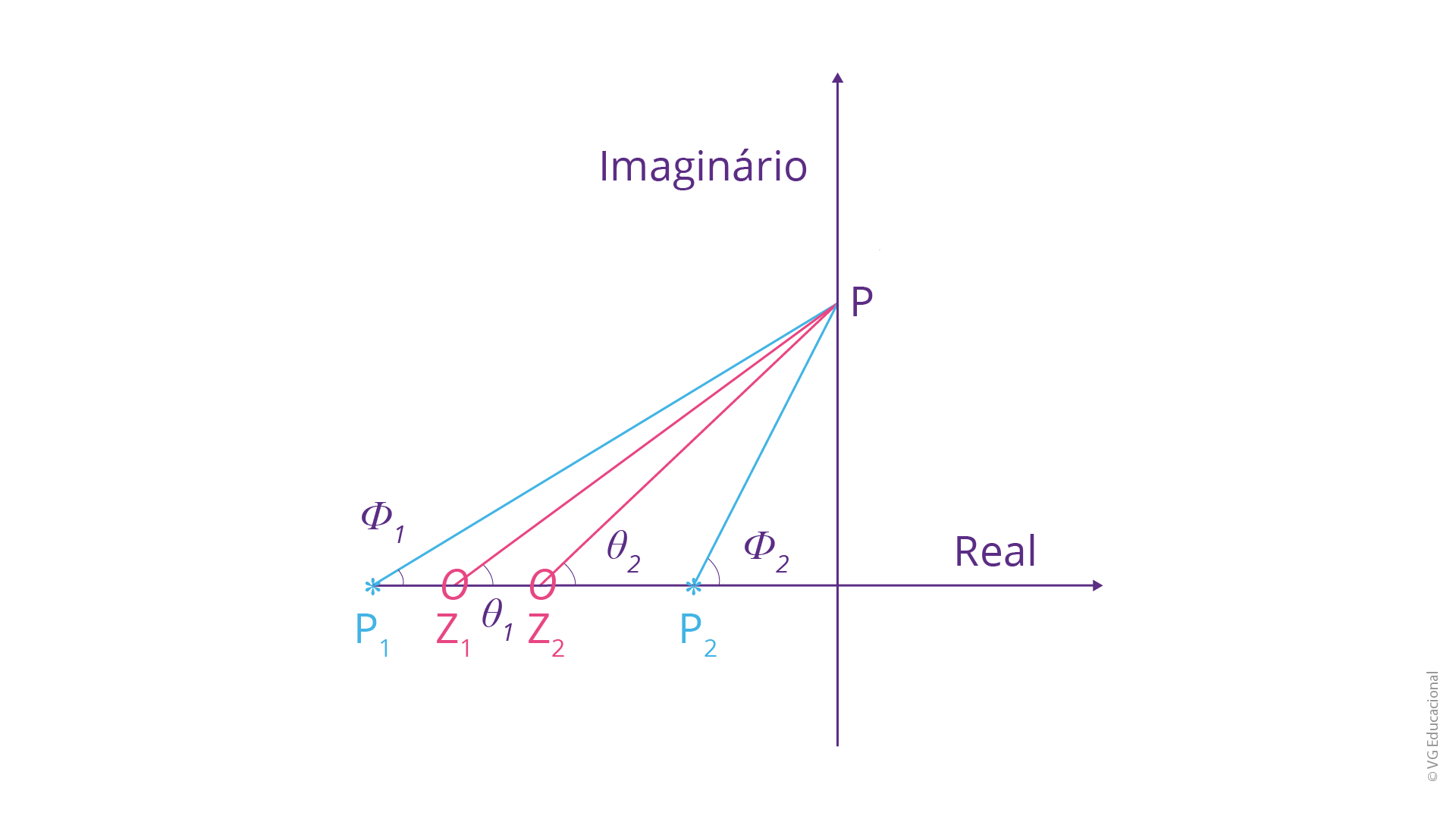
Fonte: Elaborada pelo autor.
#PraCegoVer: plano s, com o eixo real e o eixo imaginário, sendo dois polos e dois zeros, localizados no eixo real. Em ordem crescente de magnitude, tem-se o polo 1, formando o ângulo \({{\phi }_{1}}\) considerando a projeção do ponto P no eixo imaginário. O zero 1 forma o ângulo \({{\theta }_{1}}\), com esse mesmo ponto, seguido pelo zero 2, com o ângulo \({{\theta }_{2}}\) nesse mesmo ponto de referência e, por fim, o polo 2, com o ângulo \({{\phi }_{2}}\), com relação ao ponto P.
A seguir, veremos o passo a passo de como proceder com o projeto de um controlador, mais especificamente um tipo de compensador em avanço de fase, para um processo modelado a partir de uma função de transferência e com especificações práticas.
Exemplos Práticos
Considere então, como exemplo prático, que desejamos projetar um sistema de controle para a compensação de um sistema, visando aperfeiçoar o regime permanente em 10 vezes, além de considerar o fator de amortecimento em 0,174.
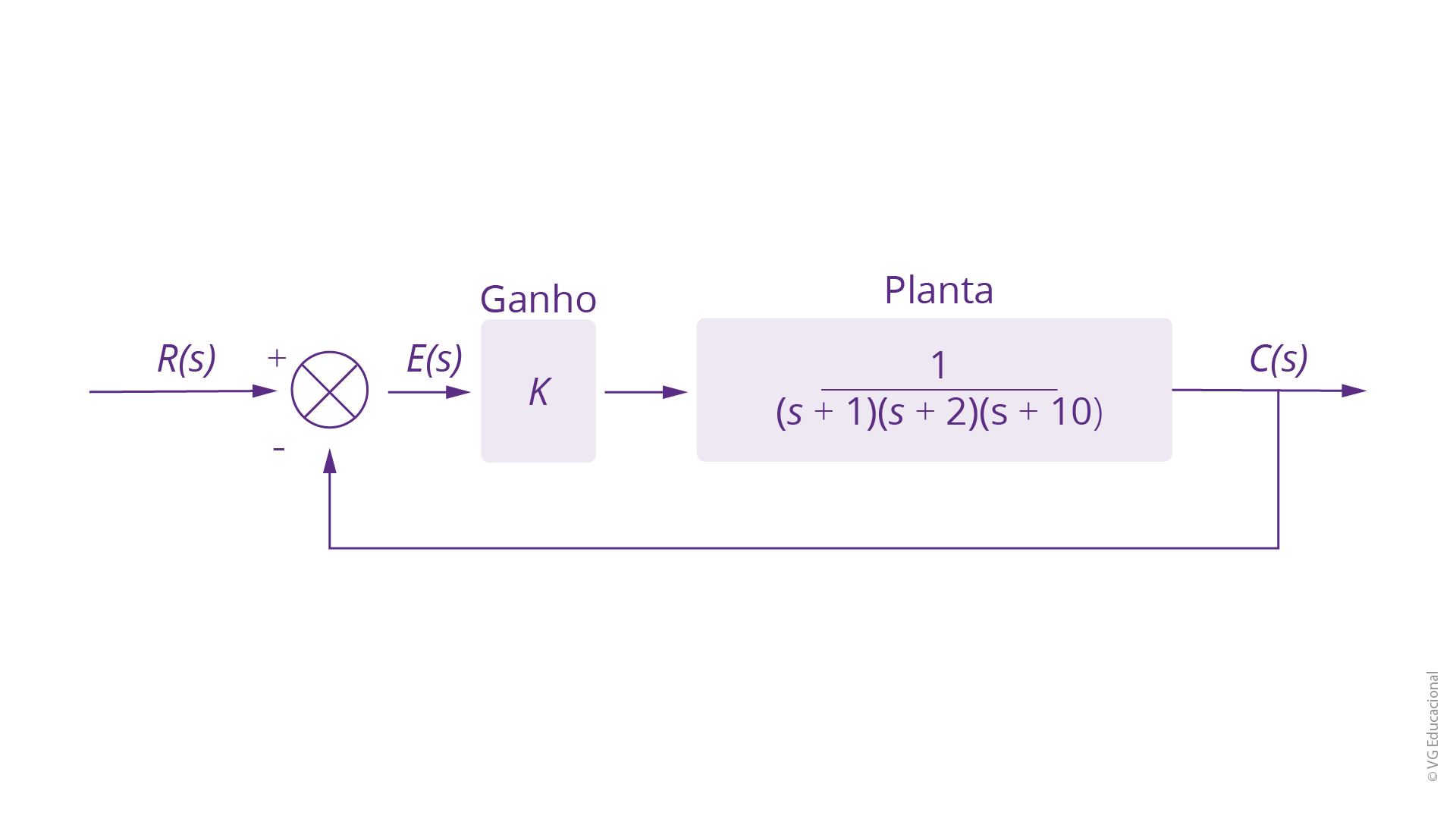
Fonte: Adaptada de Nise (2018).
#PraCegoVer: diagrama de blocos com R(s) de entrada, uma junção de soma, o erro E(s), o bloco ganho K, a planta \(1/\left( s+1 \right)\left( s+2 \right)\left( s+10 \right)\), que é representada por um bloco, e a saída C(s), que está conectada à junção em realimentação unitária.
Tem-se, ainda, o lugar geométrico das raízes desse sistema, que pode ser visto na figura a seguir.
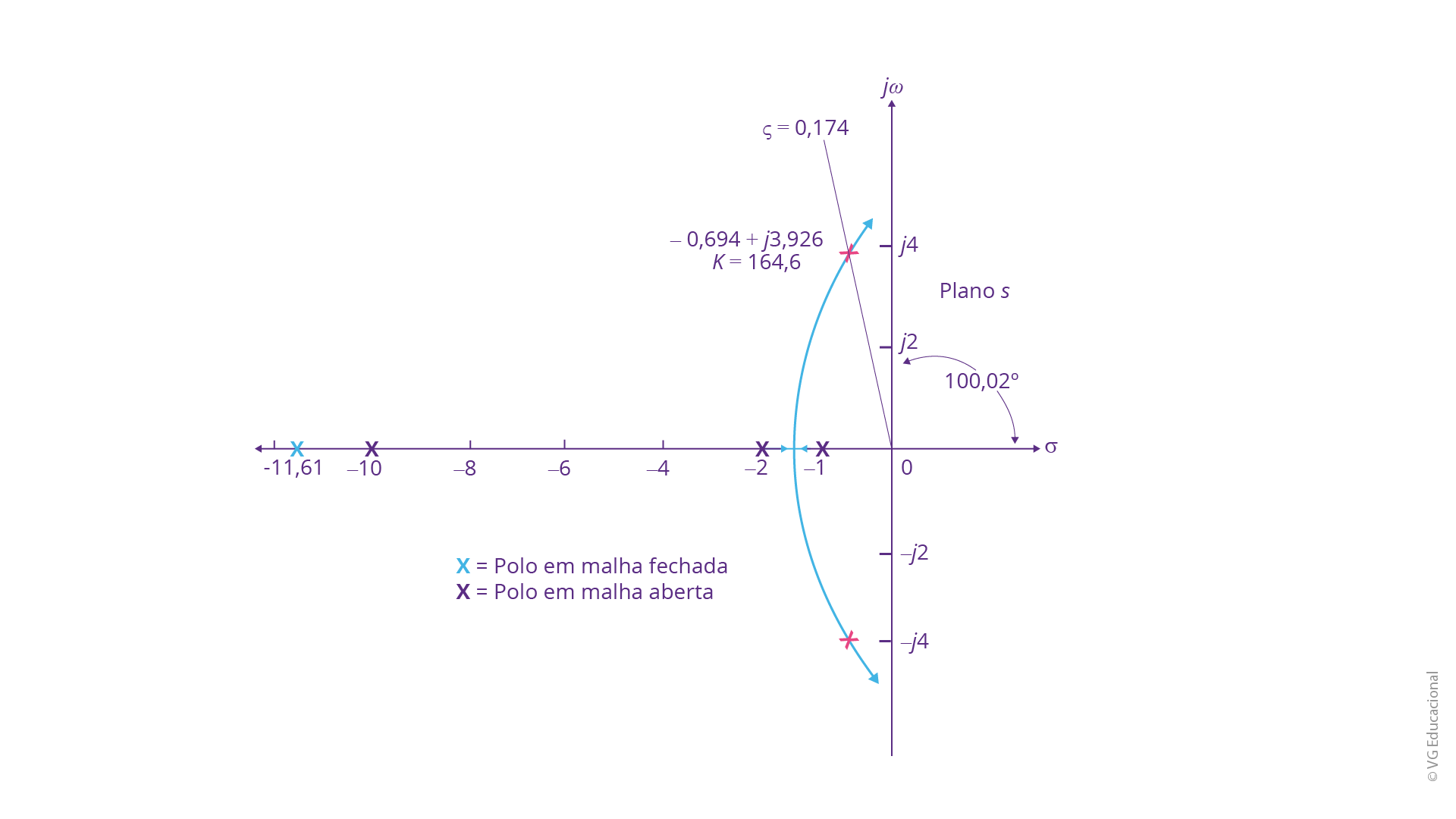
Fonte: Nise (2018, p. 685).
#PraCegoVer: plano s, com o eixo real \(\sigma \) e o eixo imaginário \(j\omega \). São representados os polos em malha aberta em negrito, com x em -10, -2 e -1, os polos em malha fechada, -11,61, -0,694 + j3,926 e -0,694 - j3,926, com um semicírculo entre eles. A reta \(\varsigma =0,174\) forma um ângulo de 100,02° com o eixo real.
O primeiro passo será estabelecer o erro sem a compensação. Considerando o fator de amortecimento em 0,174, constata-se, através do lugar geométrico das raízes, que existirão os polos dominantes, \(-0,694\pm j3,926\), para um dado ganho de 164,6. O terceiro polo dominante será encontrado de forma semelhante e, para o caso apresentado, -11,61, o que resulta em um ganho Kp = 8,23, permitindo calcular o erro em regime permanente. Vale lembrar que, novamente, a utilização de software será de fundamental importância.
\[e\left( \infty \right)=\frac{1}{1+{{K}_{p}}}=0,108\]
Uma melhoria em 10 vezes significará um erro em regime permanente de 0,0108, o que nos levaria a um ganho de:
\[{{K}_{p}}=\frac{1-0,0108}{0,0108}=91,59\]
Além disso, comparando o sistema (sem e com o compensador), a relação é proposta, permitindo estabelecer o zero do compensador em função de seu polo, ou vice-versa. Veja:
\[\frac{{{z}_{c}}}{{{p}_{c}}}=\frac{K{{p}_{comp}}}{K{{p}_{sem}}}\]
Tendo pc = 0,01, obtemos:
\[{{z}_{c}}=\frac{91,59}{8,23}{{p}_{c}}=11,13{{p}_{c}}=0,111\]
Assim, a função de transferência do compensador será:
\[{{G}_{c}}\left( s \right)=\frac{K\left( s+0,111 \right)}{\left( s+0,01 \right)}\]
Além disso, comparando o sistema compensado e o não compensado, mais especificamente o lugar geométrico das raízes do sistema em malha aberta resultante, pós-compensação, fica fácil perceber o efeito da inserção de polos e de zeros, estabelecidos através da colocação do compensador no sistema controlado. Logo, teremos:
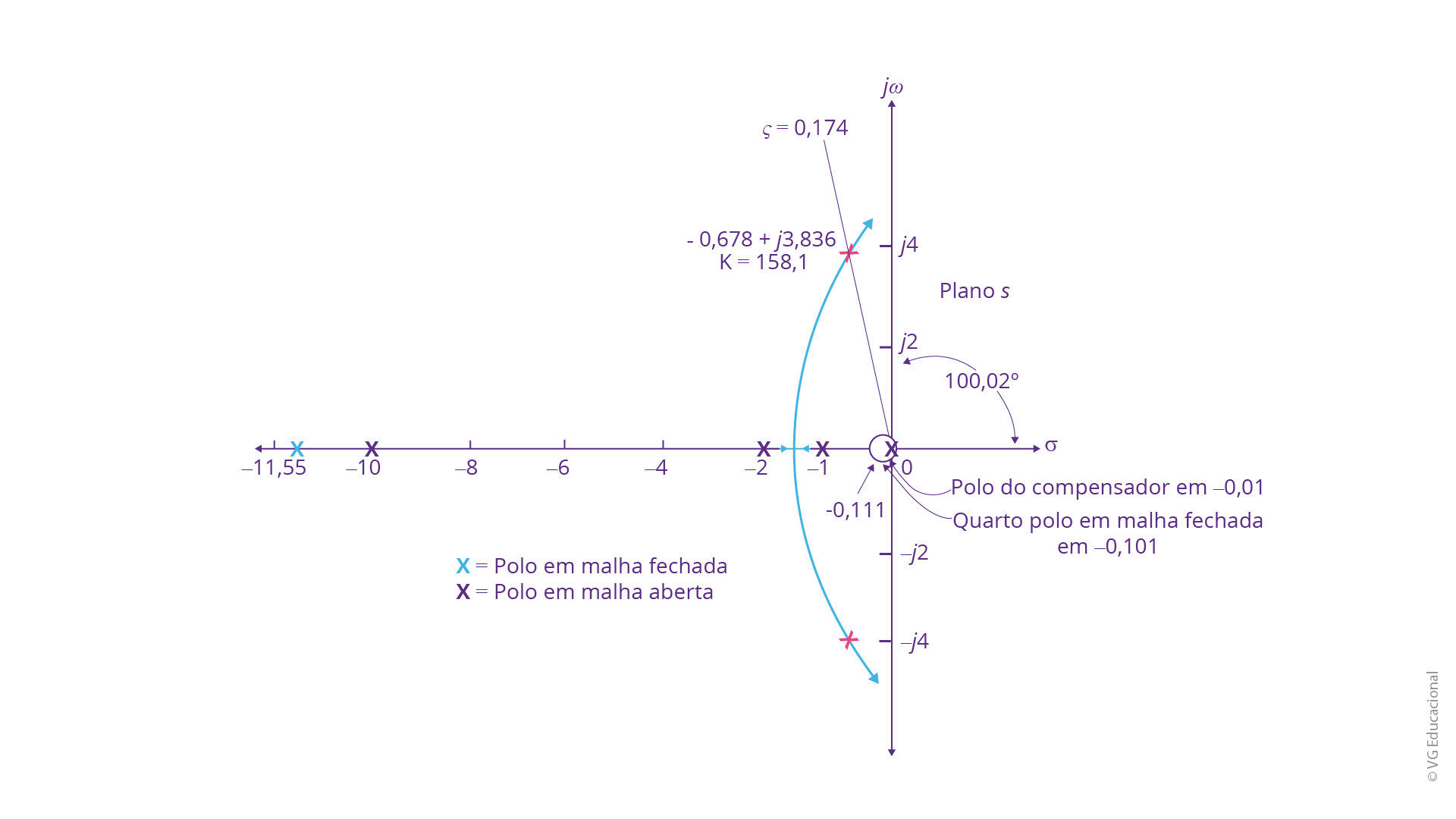
Fonte: Nise (2018, p. 691).
#PraCegoVer: plano s, com o eixo real \(\sigma \) e o eixo imaginário \(j\omega \). Desenha-se os polos em malha fechada, em malha aberta e os zeros, além de considerar K = 158,1 e \(\varsigma -0,174\). Os polos em malha aberta são: -10, -2, -1 e -0,101. Os polos em malha fechada são: -11,55, -0,01, -0,678 + j3,836 e -0,678 - j3,836. A reta dada por \(\varsigma =0,174\) faz um ângulo de 100,02° com o eixo real.
Lembre-se que a obtenção do lugar geométrico das raízes para o sistema compensado segue os mesmos passos vistos anteriormente. Ademais, processos semelhantes poderão ser realizados para o projeto de um compensador em avanço de fase ou, até mesmo, para um compensador em avanço e em atraso. Além disso, será de fundamental importância, como você já deve ter percebido, a validação da presença do compensador, pois, em alguns casos, outros ajustes poderão ser necessários, visando ao desenvolvimento final do sistema de controle.
Considere, para análise prática e interpretação de possíveis efeitos proporcionados pelo sistema de controle, o exemplo visto anteriormente: projeto de um compensador em atraso de fase. Para tomar a decisão final, devemos ponderar alguns aspectos. Caso o compensador seja ou não uma boa opção para uso na prática, a análise do lugar das raízes deverá ser feita e, como vimos anteriormente, a utilização de software poderá contribuir de maneira significativa nesse processo. Pensando nisso, analise o resultado permitido pelo sistema compensado. Qual foi o efeito conseguido com a inserção do compensador? Utilize, em sua explicação, os polos e os zeros do sistema, além do seu erro em regime permanente.
Através do lugar geométrico das raízes é possível perceber a modificação proporcionada nos polos em malha fechada do sistema, mas isso faz parte dos efeitos da compensação. Além disso, falando em efeitos específicos — inserção de polos e de zeros, observa-se que, no caso apresentado, a inserção de um quarto polo no sistema, por conta do compensador, levou ao cancelamento do zero existente anteriormente, fazendo parte, também, da ação de controle proporcionada. Por fim, com relação ao erro em regime permanente, percebemos que o valor foi muito próximo ao especificado, com redução em 10x, obtendo, por conseguinte, uma fração de 1/9,818.
Iniciaremos nossos estudos a partir de uma visão geral, entendendo o desenvolvimento do diagrama, para que, posteriormente, possamos compreender, através de exemplos práticos, a justificativa para a utilização dos software como, por exemplo, a acessibilidade para a obtenção dessas análises, bem como a criação de um critério de estabilidade. Vamos lá?
Visão Geral
O Diagrama de Bode é um tipo de gráfico logarítmico utilizado para a representação de um dado sistema de controle, ou de um processo ou de uma planta, no domínio da frequência.
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Commodo ullamcorper a lacus vestibulum sed arcu. Vel facilisis volutpat est velit egestas dui id ornare. Quis imperdiet massa tincidunt nunc pulvinar sapien et ligula.
Massa massa ultricies mi quis. Semper viverra nam libero justo. Sed tempus urna et pharetra pharetra massa massa. Nunc eget lorem dolor sed viverra. Quam pellentesque nec nam aliquam sem. Vulputate odio ut enim blandit volutpat maecenas volutpat. Maecenas accumsan lacus vel facilisis. Est sit amet facilisis magna. Tellus integer feugiat scelerisque varius morbi enim nunc faucibus.
Utilizamos representações logarítmicas por dois motivos: para facilitar a visualização total da resposta, considerando que a frequência varia em valores muito baixos, mas também privilegiando casos em que temos variações de ordem de 10² ou mais.
Na verdade, essa representação logarítmica ocorre através de duas performances que, em conjunto, denotam a resposta completa em frequência. Um Diagrama de Bode é formado a partir da resposta do módulo e da fase da função de transferência, capaz de representar matematicamente o sistema a ser estudado. Sendo uma função de transferência qualquer, será interessante transformá-la de acordo com a exemplificação a seguir, evidenciando os n polos e m zeros,
\[G\left( s \right)~=~\frac{K\left( s+{{z}_{1}} \right)\left( s+{{z}_{2}} \right)...\left( s+{{z}_{m}} \right)}{\left( s+{{p}_{1}} \right)\left( s+{{p}_{2}} \right)...\left( s+{{p}_{n}} \right)}\]
Nesse caso, K pode ser um ganho presente (ou não, em alguns casos). Além disso, representaremos o sistema em malha aberta — o motivo para essa escolha ficará claro no nosso primeiro exemplo prático do uso do Diagrama de Bode, no próximo tópico.
No domínio da frequência, podemos tornar a função escrita na forma \(G\left( j\omega \right)\). Assim, a magnitude da resposta será:
\[magnitude~=~20log\left| G\left( j\omega \right) \right|\]
Já a fase, por sua vez, é calculada a partir do número em sua forma complexa. O Diagrama de Bode será, ainda, o resultado de um esboço “otimizado”, frente às aproximações/referências. Como exemplo para compreensão, considere a seguinte função de transferência.
\[G\left( s \right)~=~\frac{10\left( s+3 \right)}{s\left( s+2 \right)\left( {{s}^{2}}+s+2 \right)}\]
Logo, considerando e normalizando a função, temos:
\[G\left( j\omega \right)=\frac{3.10\left( \frac{j\omega }{3}+1 \right)}{2.2\left( j\omega \right)\left( \frac{j\omega }{2}+1 \right)\left[ \frac{{{\left( j\omega \right)}^{2}}}{2}+\frac{j\omega }{2}+1 \right]}=\frac{37,5\left( \frac{j\omega }{3}+1 \right)}{\left( j\omega \right)\left( \frac{j\omega }{2}+1 \right)\left[ \frac{{{\left( j\omega \right)}^{2}}}{2}+\frac{j\omega }{2}+1 \right]}\]
Agora, precisaremos definir as assíntotas de curvas retas, que servirão de referência para o desenho, de acordo com o formato da função. Nesse caso em específico, teremos:
\[1{}^\text{a}~ass\acute{i}ntota:~7,5;~2{}^\text{a}~ass\acute{i}ntota:~1/j\omega ;~3{}^\text{a}~ass\acute{i}ntota:~\frac{j\omega }{3}+1;~4{}^\text{a}~ass\acute{i}ntota:~\frac{1}{\frac{j\omega }{2}+1};\]
\[5{}^\text{a}~ass\acute{i}ntota:~\frac{1}{\frac{{{\left( j\omega \right)}^{2}}}{2}+\frac{j\omega }{2}+1}\]
O próximo passo é definir as frequências de canto, pontos nos quais haverá mudanças de inclinação da curva de resposta, tanto para a magnitude quanto para a fase. Esses valores são definidos a partir dos polos e dos zeros, de acordo com o exemplo apresentado abaixo:
\[{{\omega }_{1}}=3~rad/s;~{{\omega }_{2}}=2~rad/s;~{{\omega }_{3}}=\sqrt{2}rad/s;\]
Com todos esses parâmetros, poderemos traçar as assíntotas no Diagrama de Bode, que servirão para a obtenção da curva real, tanto para a magnitude quanto para a fase. Vejamos, mais detalhadamente, no exemplo a seguir.
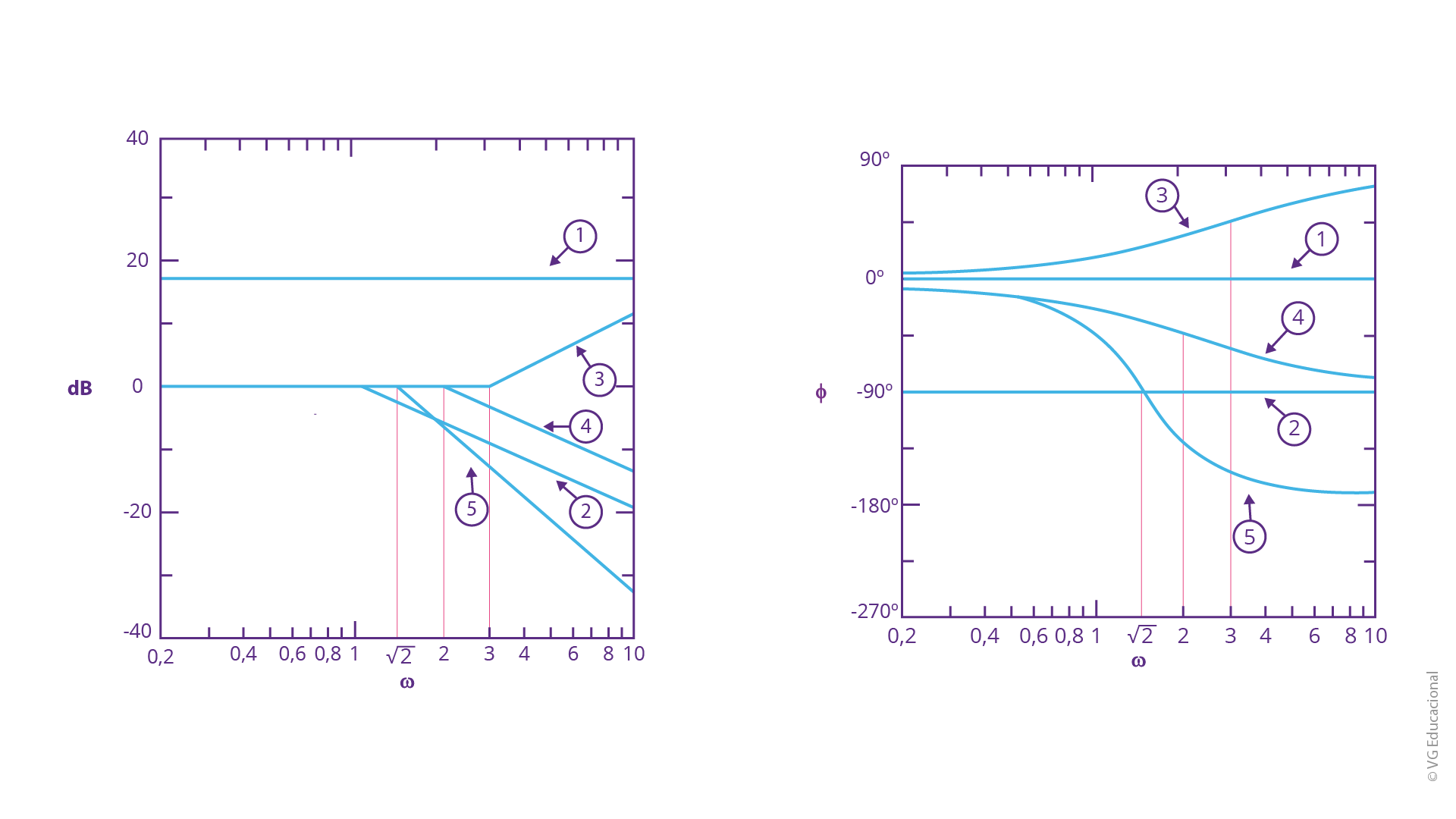
Fonte: Adaptada de Ogata (2010).
#PraCegoVer: do lado esquerdo, tem-se o gráfico de magnitude, em \(\omega \) e dB, com cinco curvas traçadas. A primeira é uma linha reta, abaixo de 20 dB. A segunda é uma linha de 0 dB até 1 rad/s. A terceira é uma linha de 0 dB até 3 rad/s. A quarta é uma linha de 0 dB até 2 rad/s e a quinta é uma linha de 0 dB até \(\sqrt{2}\) rad/s. Do lado direito, tem-se o gráfico de fase, em \(\omega \) e \(\phi \), com cinco curvas traçadas. A primeira é uma reta em 0°, a segunda é uma reta em -90°, a terceira é constante em 0° até 1 rad/s, a quarta começa em 0° e decai, especialmente a partir de 2 rad/s, para próximo de -90° e a quinta começa em 0° e decai, especialmente a partir de \(\sqrt{2}\) rad/s, quando está em -90° e, depois, assume -180°.
Cada reta corresponde a um fator da função. Traçando as assíntotas do gráfico de magnitude, nota-se que, abaixo de \(\sqrt{2}~rad/s\) ,a inclinação deverá assumir seu primeiro valor: -20 dB por década de variação da frequência. Lembremo-nos que, nesse caso, iremos contabilizar um fator 10 de variação. Por exemplo: se a frequência é 2 rad/s, logo, uma década abaixo, 0,2 rad/s, uma acima, 20 rad/s. Já entre \(\sqrt{2}\) e 2 rad/s, temos uma nova variação, em detrimento da mudança da frequência de corte e da inclinação, tornando-se -60 dB/década, entre 2 e 3 rad/s. Em seguida, passaremos para a inclinação máxima, -80 dB/década, sendo que, após 3 rad/s, a inclinação retornará para -60 dB/década. As mesmas observações são válidas com relação ao diagrama de fase, e com cada um dos fatores, para a construção da curva.
Por fim, será possível obter as curvas reais, conquistadas através da soma das curvas assíntotas, com pequenos desvios. Vejamos:
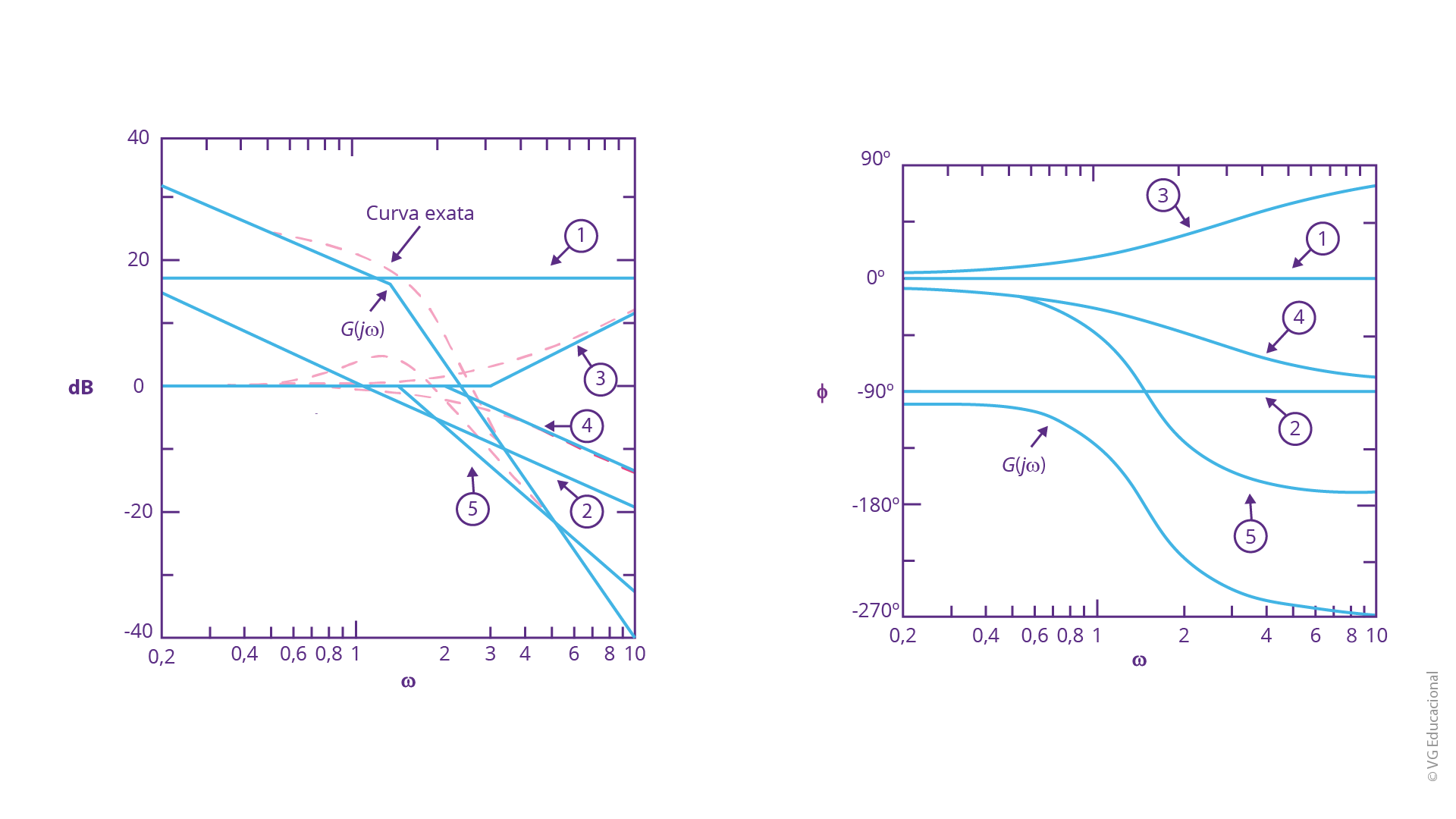
Fonte: Adaptada de Ogata (2010).
#PraCegoVer: do lado esquerdo, tem-se o gráfico de magnitude, em \(\omega \) e dB, com seis curvas traçadas. A primeira é uma linha reta, abaixo de 20 dB. A segunda é uma linha de 0 dB até 1 rad/s. A terceira é uma linha de 0 dB até 3 rad/s. A quarta é uma linha de 0 dB até 2 rad/s e a quinta é uma linha de 0 dB até \(\sqrt{2}\) rad/s. O entorno de cada uma dessas curvas representa as curvas reais, que contém pequenos desvios em torno das frequências de canto e a sexta curva é a curva exata, resultado da soma das outras cinco, junto a sua curva real. Do lado direito, tem-se o gráfico de fase, em \(\omega \) e \(\phi \), com seis curvas traçadas. A primeira é uma reta em 0°, a segunda é uma reta em -90°, a terceira é constante em 0° até 1 rad/s, a quarta começa em 0° e decai, especialmente a partir de 2 rad/s, para próximo, de -90°, e a quinta começa em 0° e decai, especialmente a partir de \(\sqrt{2}\) rad/s, quando está em -90° e, depois, assume -180°. Além disso, representando a curva \(G\left( j\omega \right)\), temos a sexta curva, que sai de -90° e decai, especialmente a partir de 1 rad/s, até atingir -270°.
Para fatores de primeira ordem, do tipo \({{\left[ j\omega \right]}^{\pm 1}}\), a correção sugerida para a curva real, aplicada na frequência de canto, é de 3 dB e 1 dB para as frequências, uma oitava abaixo e uma acima da frequência de canto. Já as correções para fatores de segunda ordem (ou quadráticos, como também são conhecidos), do tipo \({{\left[ {{\left( \frac{j\omega }{{{\omega }_{n}}} \right)}^{2}}+2\varsigma \left( \frac{j\omega }{{{\omega }_{n}}} \right)+1 \right]}^{\pm 1}}\), são dadas conforme o valor calculado de coeficiente de amortecimento. A título de exemplificação de estudo, esse tipo de correção pode ser visualizado com mais detalhes na referência de Ogata (2010). Todavia, para o sistema apresentado, devemos seguir o seguinte cálculo:
\[\frac{1}{\sqrt{2}/2}=0,353\]
A seguir, apresentarei exemplos práticos de como podemos utilizar o Diagrama de Bode em análises e, também, como é possível obter as importantes representações de um dado sistema qualquer através do uso de software.
Exemplos Práticos
Você deve estar se perguntando: por que representar o sistema no domínio da frequência? Outro questionamento plausível seria: por que devemos representar sua resposta e quais seriam as possíveis vantagens? A estabilidade de um dado sistema de controle, ou mesmo de um processo — característica tão desejada na prática, levando em consideração que são modelados no domínio da frequência, pode ser analisada através de ferramentas de representação gráfica da resposta do sistema. Assim, a partir da metodologia, será estabelecida as condições para a estabilidade de um sistema, como é o caso do Critério de Estabilidade de Nyquist. Logo, teremos a facilitação da análise através do Diagrama de Bode. O Critério de Estabilidade de Nyquist é estabelecido para relacionar a estabilidade de um sistema em malha fechada e sua resposta, em malha aberta, no domínio da frequência, além da posição de seus polos, em malha aberta. Portanto, correlaciona-se o conhecimento acerca da resposta em frequência, em malha aberta, para determinar questões importantes de estabilidade do sistema, em malha fechada. O Critério de Estabilidade de Nyquist também permitirá afirmar que os polos de 1 + G(s)H(s) são os mesmos que os do resultado de G(s)H(s) (a malha aberta) e que os zeros de 1 + G(s)H(s) correspondem aos polos da função de transferência em malha fechada (OGATA, 2010; NISE, 2018). Para um melhor entendimento, vejamos a figura a seguir:
Ademais, temos outro ponto importante: o Diagrama de Bode pode ser utilizado na implementação do Critério de Estabilidade de Nyquist para a análise de estabilidade de um dado sistema. Isso ocorre a partir da determinação de parâmetros importantes, como a margem de ganho e a margem de fase do sistema. A margem de ganho (\({{G}_{M}}\)) é expressa em dB, sendo definida, nesse caso específico, a partir do quanto o ganho, em malha aberta, irá variar com uma defasagem de 180°, para que o sistema, configurado em malha fechada, torne-se instável. Já a margem de fase (\({{\phi }_{M}}\)), por sua vez, é a variação da defasagem do sistema em malha aberta, considerando, como base, um ganho unitário. Esse valor é capaz de fazer com que este sistema, em malha fechada, torne-se instável (NISE, 2018). Desta forma, os parâmetros são duas medidas de estabilidade e, além disso, existe uma relação com o lugar geométrico das raízes, visto que quanto mais os polos do sistema estão distantes do eixo \(j\omega \), mais estável ele será e, por consequência, apto às variações nas margens.
Como exemplo, considere o seguinte sistema.
Logo, objetivando analisar a estabilidade, a planta a ser controlada possui a seguinte função de transferência:
\[G\left( s \right)~=~\frac{K}{\left( s+2 \right)\left( s+3 \right)\left( s+4 \right)}\]
Assim, o objetivo, será determinar uma faixa de K em um sistema estável. Partindo da determinação dos polos em malha aberta do sistema, obtemos:
\[G\left( s \right)H\left( s \right)~=~\frac{K}{\left( s+2 \right)\left( s+3 \right)\left( s+4 \right)}.1=\frac{K}{\left( s+2 \right)\left( s+3 \right)\left( s+4 \right)}\]
As raízes do polinômio do denominador são -2, -3 e -4, todas localizadas no semiplano esquerdo do plano s. Com isto, é possível afirmar que o sistema em malha aberta é estável e, pelo Critério de Estabilidade de Nyquist, sabemos, ainda, que o sistema em malha fechada será estável caso a resposta, em frequência do sistema em malha aberta, apresente ganho menor que 1, sendo a fase 180°. Portanto, o próximo passo será determinar o Diagrama de Bode para o sistema em malha aberta, tendo o ganho unitário. Logo, calculamos o valor de K, em que s = 0. Veja:
\[\frac{K}{\left( 0+2 \right)\left( 0+3 \right)\left( 0+4 \right)}=1~\to ~K~=~24\]
Desta forma, fazendo K = 24, o Diagrama de Bode começa em 0 dB e 0°. Para o esboço do gráfico de magnitude, lembre-se que a cada frequência de canto, a inclinação muda. Na 1ª frequência de canto (\(\omega =2~rad/s\)), a inclinação é modificada para -20 dB/década e mantém-se até \(\omega =3~rad/s\) (2ª frequência de canto). A partir deste ponto, a inclinação será -40 dB/década e mantém-se até \(\omega =4~rad/s\) (3ª frequência de canto), ponto onde passa a ser -60 dB/década. Para o diagrama de fase, como mencionado, a curva começará em 0° e mantém-se neste valor até uma década antes da 1ª frequência de canto (0,2 rad/s), ponto onde a inclinação se torna -45°/década, até uma década antes da 2ª frequência de canto (0,3 rad/s). Neste último, a inclinação muda -45°/década e passa a ser -90°/década até uma década antes da 3ª frequência de canto (0,4 rad/s), onde temos a maior inclinação, -135°/década. Por fim, para as décadas posteriores às frequências de canto, percebe-se, então, que em 20 rad/s a curva assume -90°/década até 30 rad/s, quando passa a ter -45°/década até 40 rad/s, quando se torna sem inclinação. O resultado do Diagrama de Bode é visto, a seguir, com a curva real e com a aproximação que utilizamos, assim como no exemplo anteriormente apresentado (ver subtópico 3.3.1).
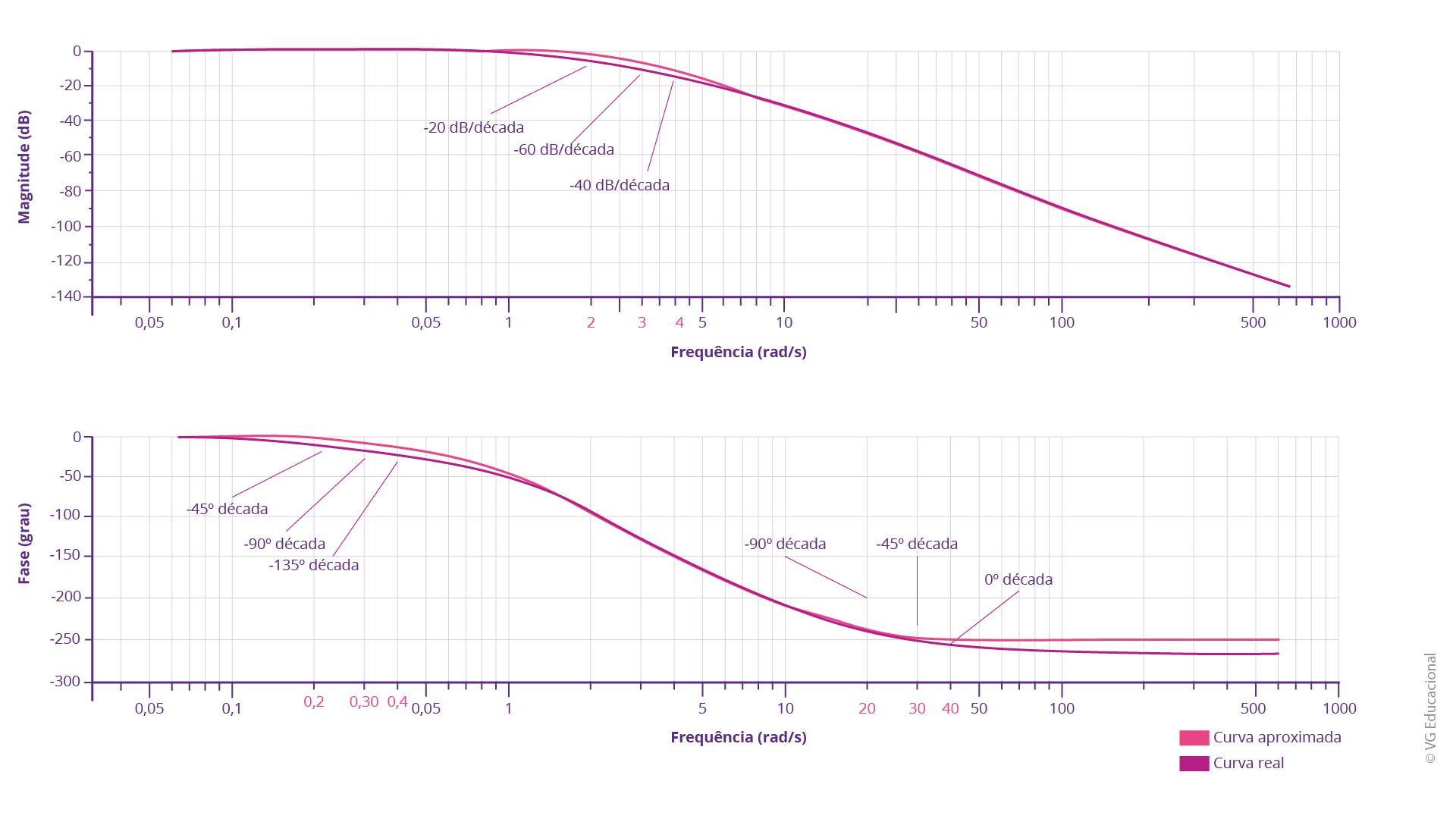
Fonte: Elaborada pelo autor.
#PraCegoVer: diagrama superior com a frequência em rad/s e a magnitude em dB, sendo representado de 0 a 1000 rad/s e -140 a 0 dB. A curva começa em 0, por volta de 0 rad/s e permanece constante até cerca de 3 rad/s, quando o decaimento é maior e chega a zero pouco depois de 500 rad/s. São representados, também, os valores vistos para decaimento, nas frequências de canto, 2, 3 e 4 rad/s. Na parte de baixo, tem-se o diagrama de frequência em rad/s por fase, em graus, variando de 0 a 1000 rad/s e -300 a 0°. Começamos a curva em 0 e 0 rad/s, aproximadamente, e decai, especialmente a partir de 0,4 rad/s, até se tornar quase constante em 20, 30 e 40 rad/s e indefinidamente, próximo a -300°.
De acordo com Nise (2018), se um contorno A — que envolve todo o semiplano da direita, for mapeado através de G(s)H(s), por conseguinte, o número de polos em malha fechada Z, no semiplano da direita, será igual ao número de polos em malha aberta P, que estão no semiplano da direita — menos o número de voltas do mapeamento no sentido anti-horário N, em torno de −1; isto é, Z = P − N.
Assim, para que o sistema seja estável, precisaremos evitar que a resposta dê voltas ao redor de -1. Em termos específicos do Diagrama de Bode, que analisa a estabilidade, percebemos que: quando a fase é -180°, temos cerca de 6 rad/s e -20 dB de magnitude, o que permite concluir que o ganho pode aumentar em até 20 dB sem que o sistema se torne instável. Sendo K = 24, no nosso caso, e o ganho de 20 dB, implica, em escala real, um ganho igual a 10. O ganho máximo para estabilidade será: 24 x 10 = 240. Assim, o sistema será estável com 0 < K < 240.
Agora, considere que você precisa determinar o Diagrama de Bode de maneira rápida. Uma opção, sem dúvida, é a utilização de software, como é o caso do Scilab. Dada a função de transferência, os seguintes comandos permitirão a obtenção do diagrama facilmente.
\[\text{s = poly(0,’s’);}\]
\[\text{num = 10*(s+3);}\]
\[\text{den = s*(s+2)*((s^2)+s+2);}\]
\[\text{t = syslin(‘c’, num/den);}\]
\[\text{clf();}\]
\[\text{bode(t,’rad’);}\]
Como último exemplo prático, apresento os possíveis passos para a obtenção do Diagrama de Bode através do MATLAB. O primeiro passo será representar a função de transferência do sistema, ainda que seu objetivo seja obtê-la de alguma outra forma. Em sequência, a partir dessa função, utilizaremos o comando e, assim, o diagrama será gerado. Logo, consideremos: num, para representar o polinômio do numerador e den para representar o polinômio do denominador:
\[\text{bode(num, den)}\]
Caso você coloque ponto e vírgula ao final, a função de transferência não será exibida na tela. Além disso, o gráfico gerado permite que você faça outras modificações, como percorrer com o cursor para ver os valores ponto a ponto, como um gráfico normal.
SAIBA MAIS
A obtenção da resposta, em frequência, pode ser realizada a partir da utilização do Diagrama de Bode, certo? Neste exemplo, trago um vídeo concernente à obtenção da resposta, em frequência, a partir de dados de um único teste (não senoidal). Além disso, tanto a função quanto o script utilizados no exemplo simulado estão disponíveis para acesso na descrição do vídeo no Youtube.
Disponível em:
Um outro ponto interessante a ser considerado, levando em conta a utilização de software, é a possibilidade de obter a função de transferência de um dado sistema a partir de seu Diagrama de Bode, seguindo o caminho inverso que tomamos aqui. A seguir, você verá, através de alguns exemplos práticos, como podemos utilizar a resposta em frequência, mais especificamente através do Diagrama de Bode, para o projeto de um controlador em um sistema físico real.
O diagrama de Bode representa a resposta, em frequência, de um dado sistema ou planta a ser controlada (ou já controlada) e, como visto anteriormente, também pode ser utilizado como ferramenta para a análise de estabilidade. Nesse sentido, é correto afirmar que:
Veremos, a seguir, como realizar o projeto de um controlador a partir do domínio da frequência, utilizando o Diagrama de Bode. Inicialmente, estudaremos a teoria por trás destes projetos e, em seguida, você verá um exemplo prático.
Visão Geral
Considere um compensador na forma a seguir:
\[{{G}_{c}}\left( s \right)~=~{{K}_{c}}\frac{\left( s+z \right)}{\left( s+p \right)}\]
A função de transferência pode, ainda, ser descrita em função de \(\alpha \), na distância entre o zero e o polo, e \(\tau \), na constante de tempo do sistema. Com isto, podemos notar, com certa facilidade, um possível ajuste para o controlador.
\[{{G}_{c}}\left( s \right)~=~{{K}_{c}}\frac{\left( \tau s+1 \right)}{\left( \alpha \tau s+1 \right)}\]
Logo, ajustando para \(0<\alpha <1\), em regime permanente, um compensador deste tipo poderá não ser a melhor opção para o sistema. Todavia, pode ser uma boa solução para o controle durante a resposta transitória. O Diagrama de Bode deste compensador, por sua vez, será:
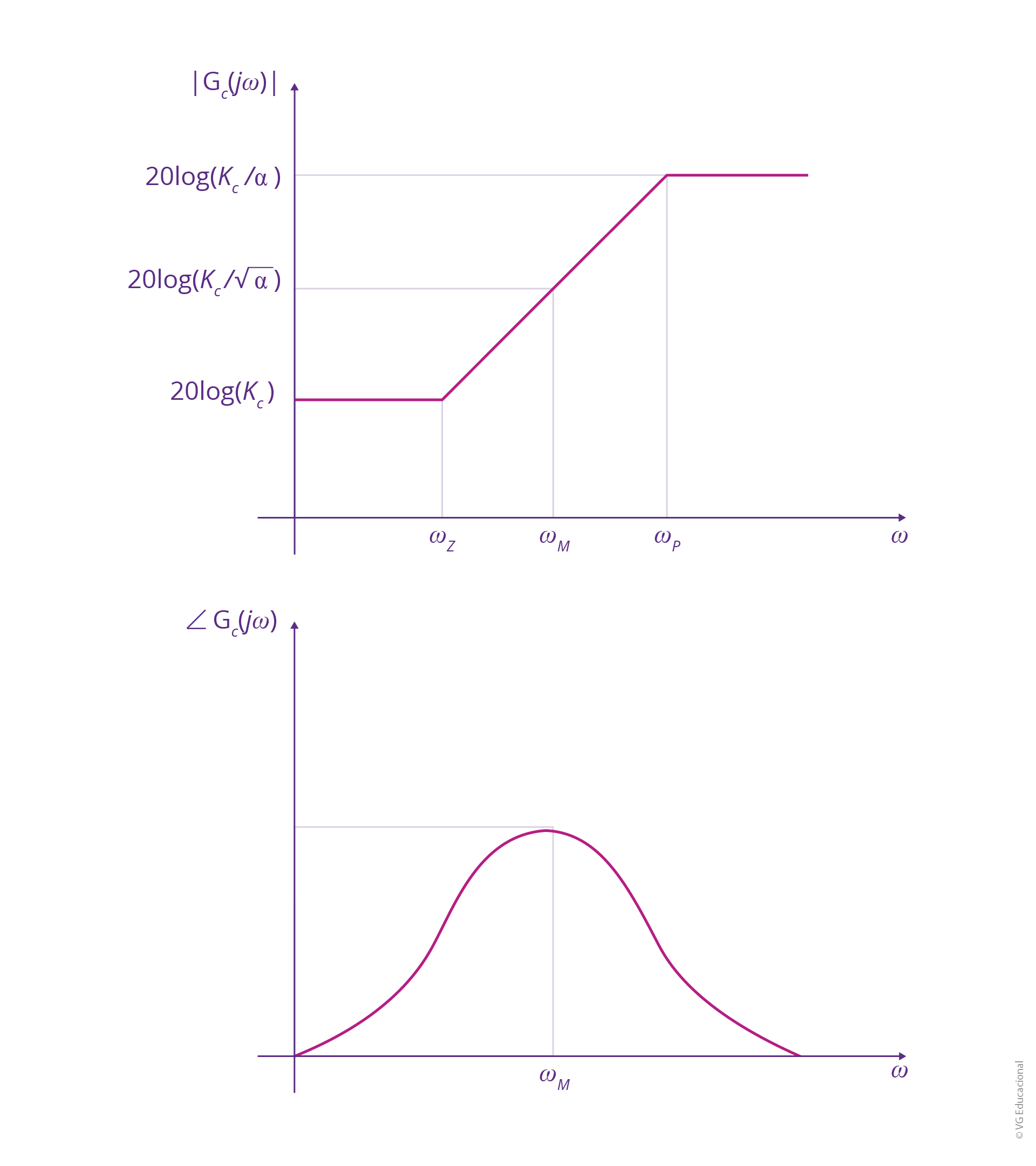
Fonte: Elaborada pelo autor.
#PraCegoVer: diagrama de magnitude na parte superior em função de \(\omega \) e \(\left| {{G}_{c}}\left( j\omega \right) \right|\), em dB, com a curva assumindo 20 log(Kc) de 0 até \({{\omega }_{z}}\). Em seguida, aumentando até \(20log\left( {{K}_{c}}/\alpha \right)\) a partir de \({{\omega }_{p}}\), sendo \(20~log~\left( {{K}_{c}}/\sqrt{\alpha } \right)\) em \({{\omega }_{M}}\). Na parte de baixo, tem-se o diagrama de fase, em função de \(\omega \) e /_ \({{G}_{c}}\left( j\omega \right)\), com a curva começando em 0 e subindo até seu valor de pico, em \({{\omega }_{M}}\), quando começa a decair.
A frequência máxima, \({{\omega }_{M}}\), é dada por:
\[{{\omega }_{M}}=\frac{1}{\sqrt{\alpha }\tau }\]
Sendo que:
\[sen\left( {{\phi }_{M}} \right)=\frac{1-\alpha }{1+\alpha }\]
Além disso, a seguinte relação é válida:
\[{{G}_{c}}\left( \infty \right)=\frac{{{K}_{c}}}{\alpha }\]
Já para o compensador em atraso, tem-se um diagrama de Bode de acordo com a figura a seguir:
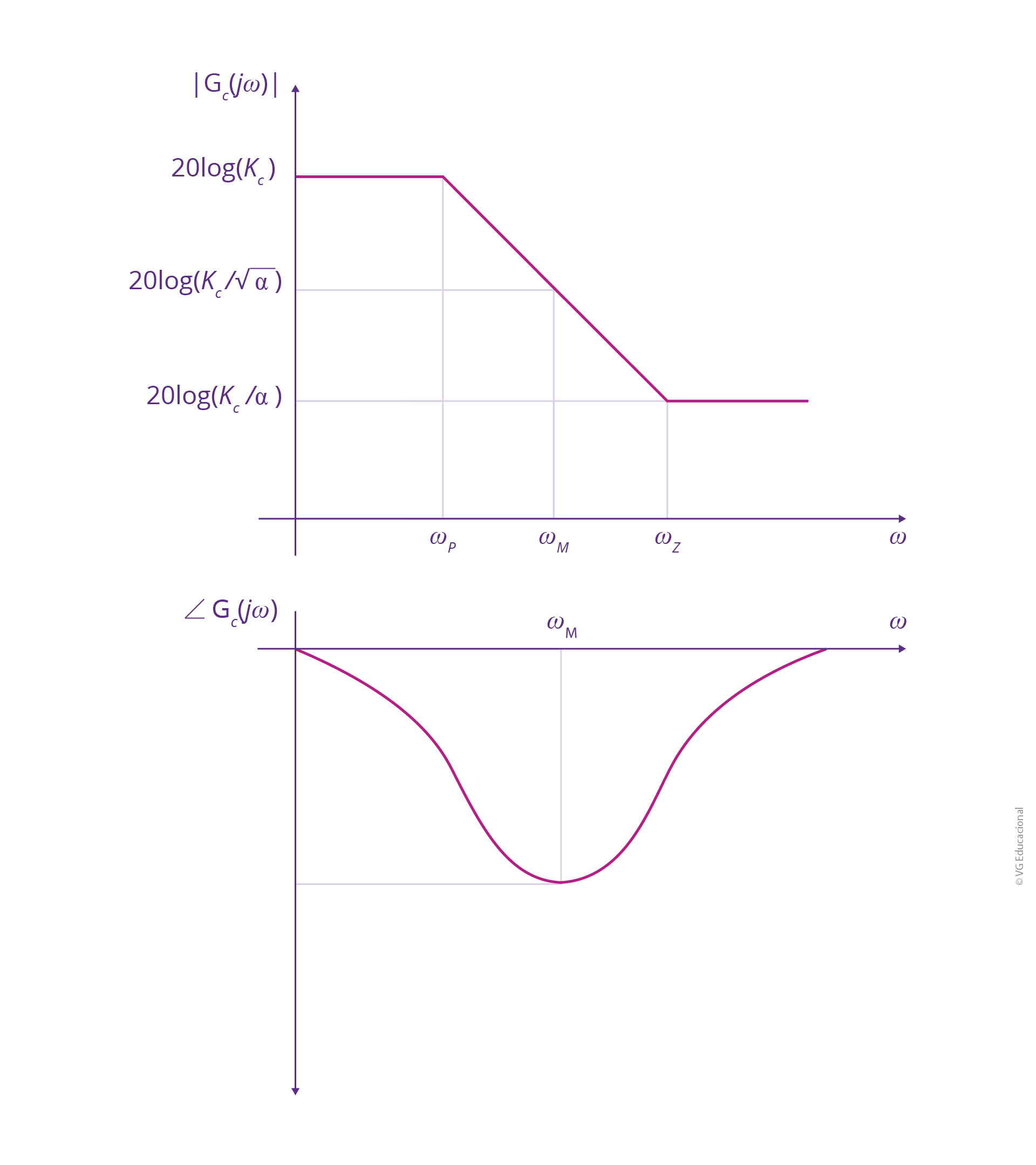
Fonte: Elaborada pelo autor.
#PraCegoVer: na parte superior, tem-se o diagrama de magnitude, com a maior de 0 até \({{\omega }_{P}}\), correspondente a 20 log(Kc). De \({{\omega }_{P}}\) até \({{\omega }_{Z}}\), a magnitude reduz para \(20~log\left( {{K}_{c}}/\alpha \right)\), sendo \(20~log({{K}_{c}}/\sqrt{\alpha }\) em \({{\omega }_{M}}\).
Admite-se que \(\alpha >1\). Logo, o polo, neste caso, é mais lento. Já no caso de um compensador em avanço e em atraso de fase, sua função de transferência pode ser reescrita como:
\[{{G}_{c}}\left( s \right)~=~{{K}_{c}}\frac{\left( {{\tau }_{1}}s+1 \right)}{\left( \left( {{\tau }_{1}}/\alpha \right)s+1 \right)}\frac{\left( {{\tau }_{2}}s+1 \right)}{\left( \left( {{\tau }_{2}}/\alpha \right)s+1 \right)}\]
De forma que \(\alpha >1~e~{{\tau }_{1}}<{{\tau }_{2}}\). Logo, o diagrama de Bode será de acordo com o exemplo a seguir:
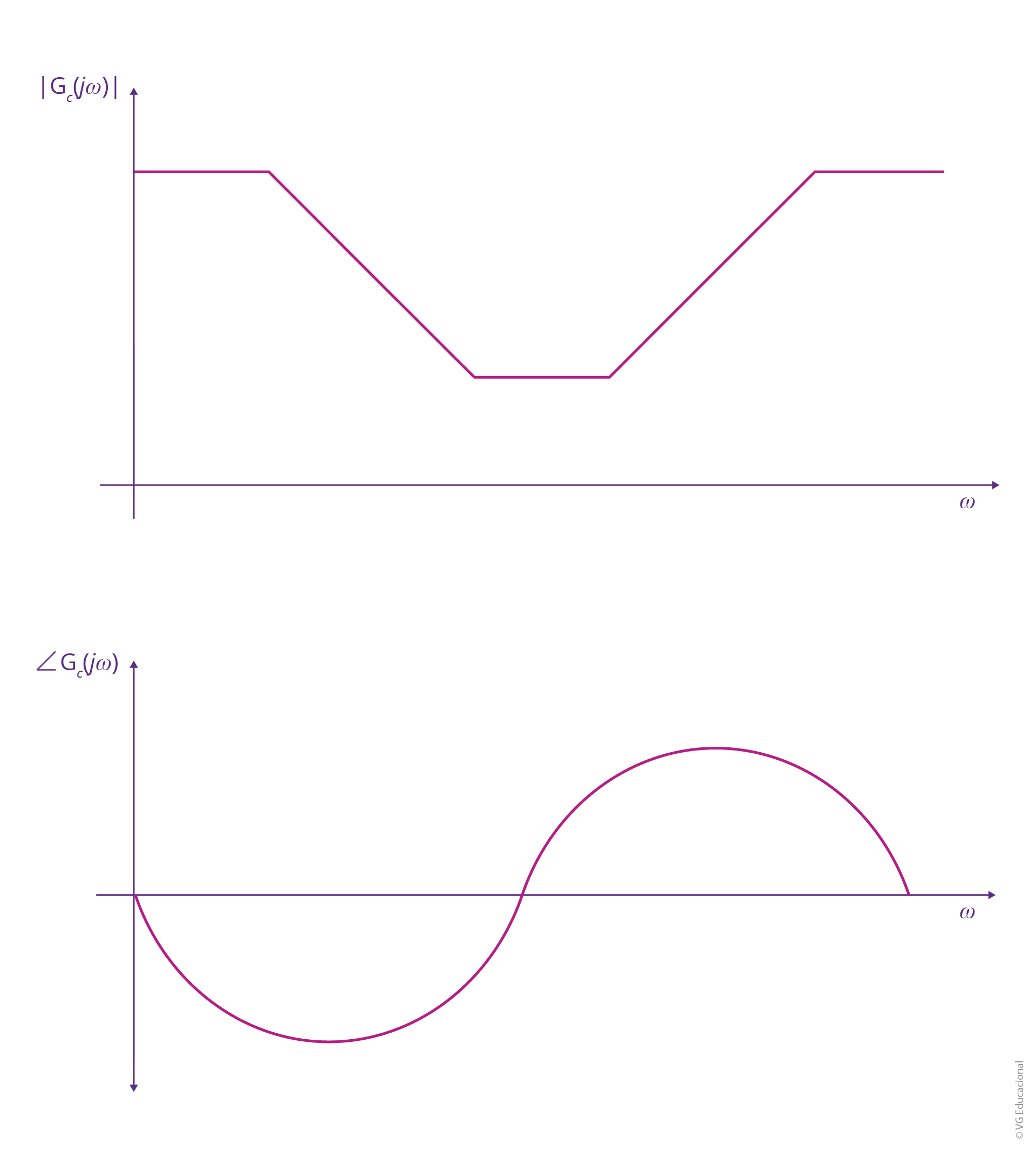
Fonte: Elaborada pelo autor.
#PraCegoVer: na parte superior, tem-se o diagrama de magnitude, com \(\omega \) no eixo x e \(|{{G}_{c}}\left( j\omega \right)\)| no y, começando em um dado valor, maior até uma certa frequência. Depois, consegue se manter constante até um outro valor e, posteriormente, sobe novamente para o mesmo valor anterior. Na parte de baixo, tem-se o diagrama de fase, com \(\omega \) no eixo x e /_\({{G}_{c}}\left( j\omega \right)\) no y, com fase negativa até certa frequência e, depois, alternando para positiva.
Posteriormente, você verá, através de um dos tipos de compensadores, como projetamos o controlador, dadas as especificações, através do Diagrama de Bode. Sendo assim, consideramos como base a questão da localização dos polos e dos zeros, além da resposta do sistema.
Exemplos Práticos
A título de exemplificação, iremos pressupor que projetaremos um controlador em atraso de fase para o sistema em malha fechada unitária de controle de uma planta com a seguinte função de transferência:
\[G\left( s \right)=\frac{100K}{s\left( s+100 \right)\left( s+36 \right)}\]
e o controlador do tipo:
\[C\left( s \right)={{K}_{c}}\frac{\left( s+z \right)}{\left( s+p \right)},\left| z \right|>\left| p \right|\]
Várias especificações práticas podem ser atendidas, mas para fins de comparação, vamos considerar que nesse sistema, em específico, desejamos determinar um ganho K, almejando a melhoria da resposta transitória do sistema, para que, ao final, fosse obtido um sobressinal de 9,5% para entrada degrau. O compensador deve funcionar para que o sistema mantenha 9,5% de sobressinal, mas, neste caso, desejamos que o erro, em regime permanente, seja 10 vezes melhor. O primeiro passo será determinar K, considerando fatores facilitadores, como estabelecer a resposta do sistema, iniciando em 0 dB em 0,1 rad/s, sendo que nos preocuparemos apenas com as frequências acima desse valor. Fazendo K = 3,6 e as condições apresentadas para facilitar os cálculos em malha aberta, teremos:
\[G\left( s \right)~=~\frac{100.3,6}{s\left( s+100 \right)\left( s+36 \right)}=\frac{360}{s\left( s+100 \right)\left( s+36 \right)}\]
Passando para a interpretação acerca das especificações para a resposta transitória do sistema, é possível concluir que:
\[\varsigma =\frac{-ln\left( sobressinal/100 \right)}{\sqrt{\pi {}^\text{2}}+ln{}^\text{2}\left( sobressinal/100 \right)}\to \varsigma \approx 0,6\]
Em seguida, passamos para o cálculo da margem de fase correspondente, com este amortecimento. Nesse caso, obtém-se:
\[{{\phi }_{M}}=t{{g}^{-1}}\left( \frac{2\varsigma }{-2{{\varsigma }^{2}}+\sqrt{1+4{{\varsigma }^{4}}}} \right)\to {{\phi }_{M}}\approx 59,2{}^\circ \]
Assim, a resposta do sistema em malha aberta, será:
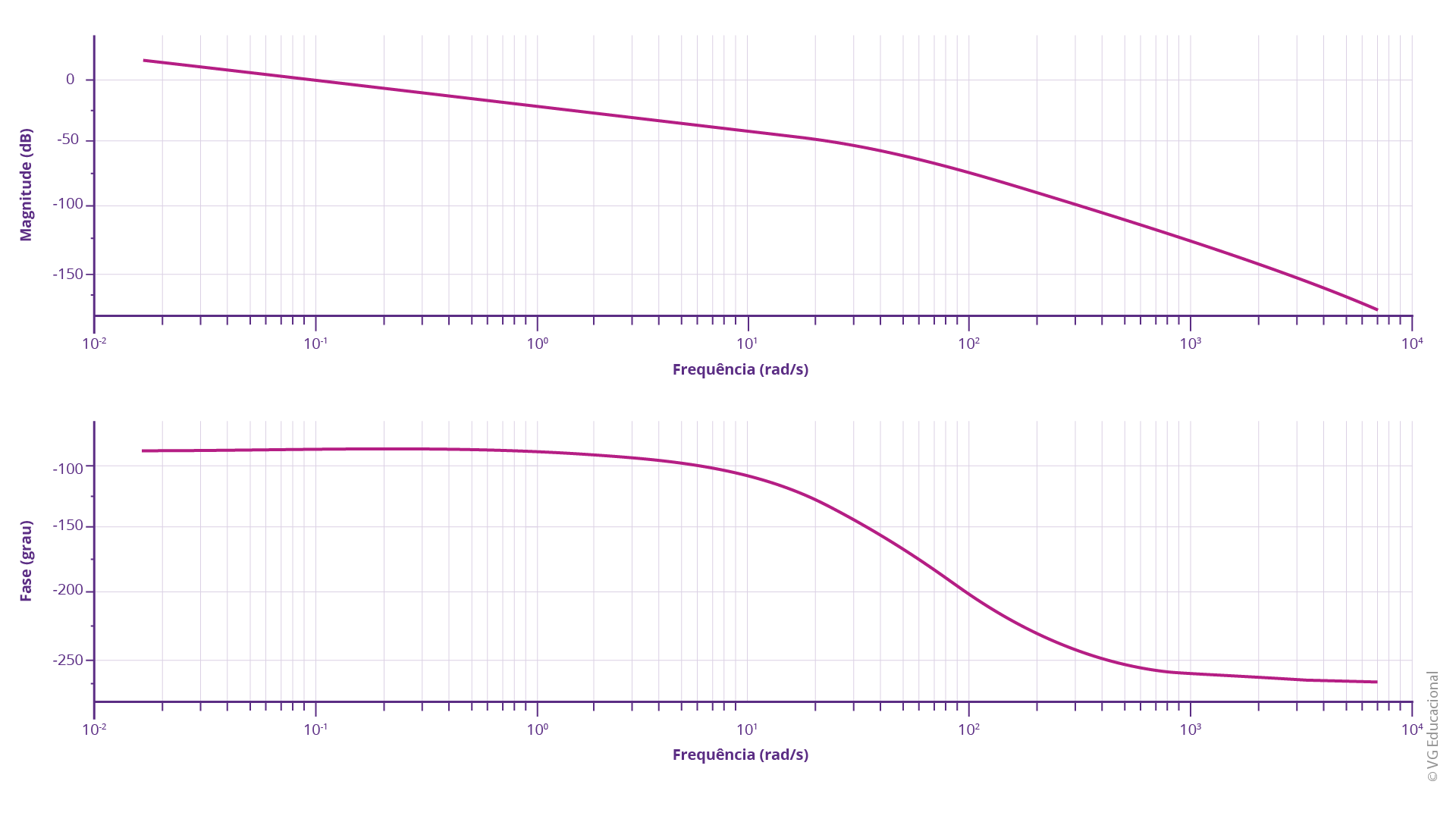
Fonte: Elaborada pelo autor.
#PraCegoVer: na parte superior, tem-se o diagrama de amplitude, com a frequência em rad/s no eixo x e a magnitude em dB no y. A curva de resposta começa próximo a 0 dB e decai ao longo da variação de frequência, especialmente a partir de 10 rad/s. Na parte de baixo, tem-se o diagrama de fase, com a frequência em rad/s no eixo x e a fase em graus no y, sendo a curva -100° até 10 rad/s, quando decai bruscamente para -250°.
Agora, buscaremos, no Diagrama de Bode, para qual frequência é estabelecida a fase de 59,2°, sendo que este cálculo deve ser feito tomando 2180° - \({{\phi }_{M}}\), resultando em 2120,8°. A frequência, que gera esta margem, pode ser calculada pela seguinte relação, onde obtemos 14,8 rad/s:
\[/ \text{_} G\left( j\omega \right)=-90{}^\circ -t{{g}^{-1}}\frac{\sqrt{-2{{\varsigma }^{2}}+\sqrt{4{{\varsigma }^{4}}+1}}}{2\varsigma }\]
Outrossim, ao projetar no gráfico a magnitude, vemos que será 244 dB, porém para que tenhamos a margem de fase requerida, adotaremos 0 dB a partir do deslocamento promovido pelo ganho K estabelecido, assim como o sobressinal desejado, de 9,5%. Ou seja:
\[20log\left( x \right)~=~44~dB~\to ~x\approx 162\]
K = 3,6.162 = 538,2
A função de transferência em malha aberta será:
\[G\left( s \right)~=~\frac{53820}{s\left( s+100 \right)\left( s+36 \right)}\]
O resultado obtido pode ser visto pelo seguinte Diagrama de Bode:
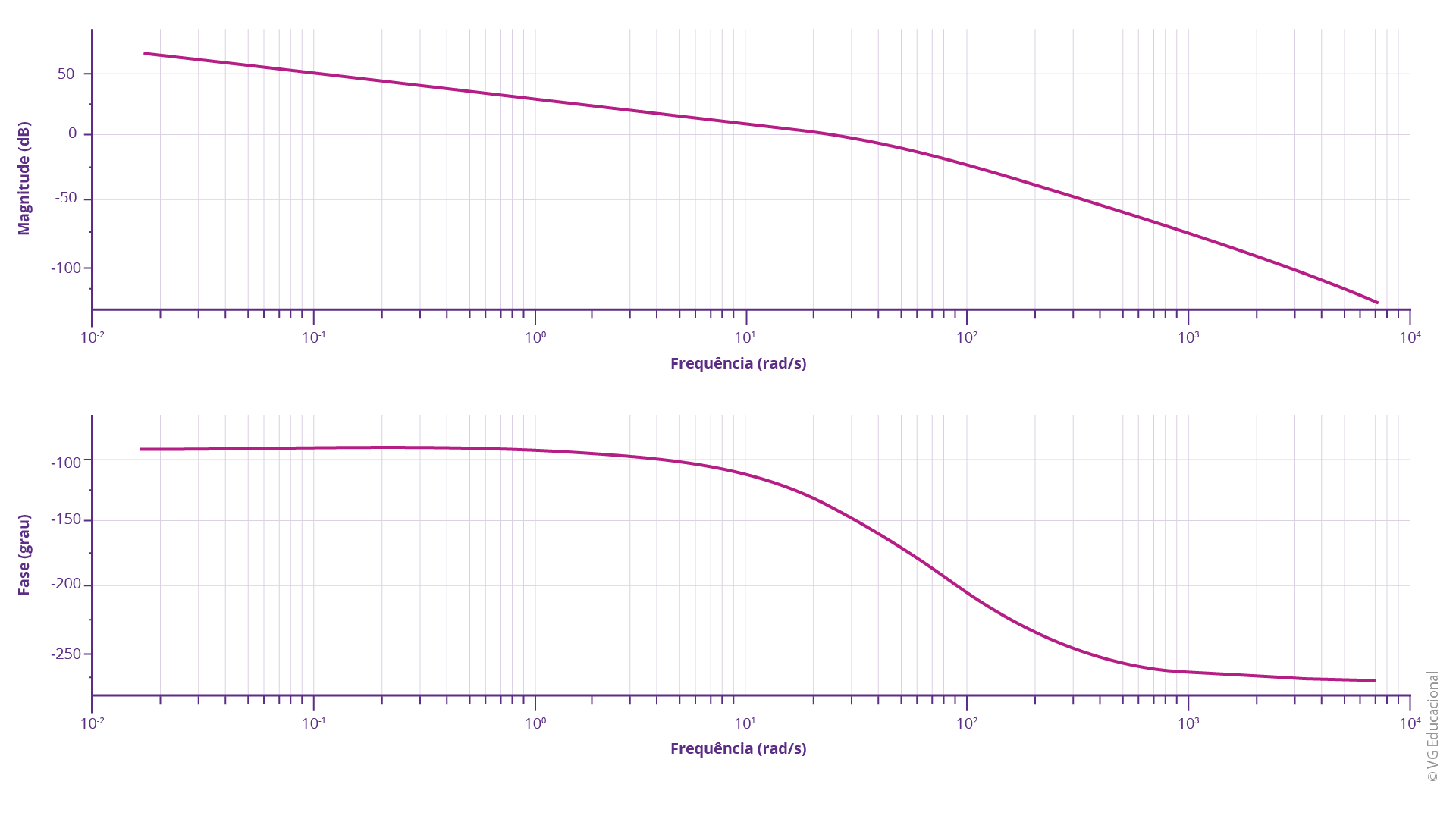
Fonte: Elaborada pelo autor.
#PraCegoVer: diagrama superior de frequência, em rad/s e magnitude, em dB. A curva apresentada parte constante, em 50 dB, para as frequências menores, com queda, que se acentua a partir de 10 rad/s, até menos de -100 dB. O diagrama inferior apresenta a frequência, em rad/s e a fase, em graus, com a curva constante em -100° até 10 rad/s e começa a decair, atingindo cerca de -200° em 100 rad/s.
Agora, de fato, obteremos a função de transferência do compensador para que, posteriormente, possa ser validado e, então, implementado. Com a solicitação apresentada do erro de regime permanente, o seguinte ganho é encontrado.
\[{{K}_{v}}=\frac{53820}{s\left( 0+100 \right)\left( 0+36 \right)}=1~\to ~{{K}_{v}}=16,2\]
Mas, com a melhoria de 10x do erro de regime permanente, conclui-se que Kv= 162. Logo, em malha aberta, tem-se que:
\[G\left( s \right)=\frac{5382}{s\left( s+100 \right)\left( s+36 \right)}\]
E, em malha fechada, temos:
\[G\left( s \right)=\frac{538200}{s\left( s+100 \right)\left( s+36 \right)}\]
Como o erro em regime permanente melhorará em 10 vezes, a margem de fase deve ser aumentada em um fator de 10. Sendo assim: 59,2° + 10° = 69,2°. A frequência correspondente deve ser encontrada: 2180° - 69,2° = 2110,8°, o que resulta em 9,8 rad/s, aproximadamente. Em seguida, estabelece-se um ganho para que, a essa frequência, o diagrama de magnitude esteja em 0 dB. Portanto, conclui-se que o compensador em projeto deverá ser capaz de fornecer 224dB para atenuação da curva de magnitude, passando de 9,8 rad/s para 0 dB.
Primeiramente, iniciaremos traçando uma assíntota de alta frequência, de acordo com o fornecimento do compensador que, no nosso caso, será em 224dB. Em seguida, deve-se escolher a frequência de canto superior que, usualmente, é estabelecida em uma década inferior à frequência encontrada para a margem de fase — no exemplo, em 0,98 rad/s. O próximo passo é interligar o ponto desejado (0 dB) até onde estamos (224dB), traçando uma reta que, nesse caso específico, terá uma inclinação aproximada de 220 dB/década. Como o ganho Kv era de 16,2, faz-se este menos o fator de 10 — 0,062 rad/s e, em seguida, escolhemos a frequência de canto inferior, uma década abaixo. Para determinar o ganho do compensador, devemos considerar o desejo de manter o valor já especificado, K = 5832. O resultado, considerando o fator de 10, será de 0,062, já que o ganho estático do compensador deve ser unitário para manter os demais ganhos especificados (NISE, 2018). Sendo assim, a função de transferência do compensador será:
\[{{G}_{c}}\left( s \right)~=~0,062.\frac{s+0,98}{s+0,062}\]
O próximo passo é obter a validação do compensador. Para isto, a utilização de software será fundamental, facilitando a obtenção da resposta em frequência e, assim, permitindo analisar o comportamento do sistema com esse compensador.
Considerando o sistema apresentado no exemplo anterior, o próximo passo é validá-lo na prática. Contudo, devemos validar a resposta no compensador, certo? Para isto, podemos obter a resposta através do sistema compensado, configurado em malha aberta, por exemplo.
Assim, suponhamos que isso seja feito. Neste caso, qual seria a resposta em frequência do sistema?
Para o caso apresentado, a resposta em malha aberta é:
\[G\left( s \right)~=0,062.\frac{s+0,98}{s+0,062}~\frac{53820}{s\left( s+100 \right)\left( s+36 \right)}= \\ 36158\frac{s+0,98}{s\left( s+100 \right)\left( s+36 \right)\left( s+0,062 \right)}\]
A resposta, em frequência, poderá ser obtida facilmente utilizando software, como o Scilab, através do uso dos comandos já apresentados anteriormente neste estudo. Sendo assim, o resultado seria:
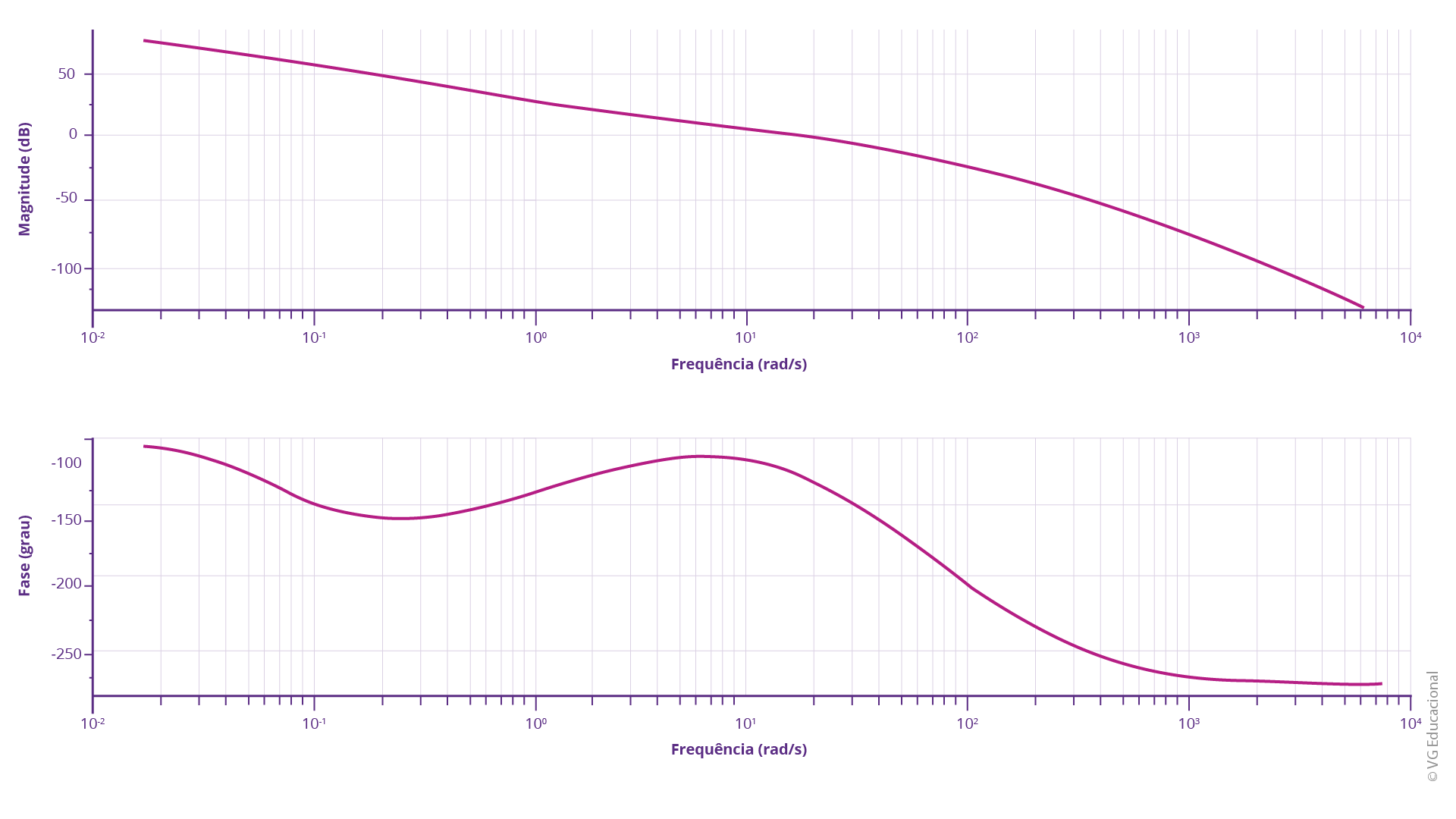
Fonte: Elaborada pelo autor.
#PraCegoVer: diagrama superior com a frequência em rad/s e a magnitude em dB. A curva representada possui amplitude inicial acima de 50 dB e decai ao longo da variação de frequência, até menos de -100 dB. Na parte inferior, tem-se um diagrama de frequência em rad/s em função da fase, em graus. A curva obtida começa em -100°, diminuindo até -150°, cerca de 0,1 rad/s, aumentando novamente para cerca de -100°. A partir de 1 rad/s e a partir de 10 rad/s começa a decair, até um pouco abaixo de -250°.
Projeto LR: Controlador PID
Canal: Luis Antônio Aguirre
Comentário: Como vimos, o projeto de um controlador pode ser realizado através de diversas técnicas de representação do sistema e, também, através da análise da resposta. Nessa videoaula, é possível ver mais detalhes sobre o projeto de um controlador PID através do lugar das raízes, incluindo a utilização do software MATLAB.
Disponível em:

Controle Automático
Autores: Plínio de Lauro Castrucci, Anselmo Bittar e Roberto Moura Sales
Editora: LTC
Capítulo: 4
Ano: 2018
ISBN: 9788521635611
Comentário: O livro possui uma ótima abordagem acerca do controle automático de sistemas. Sugiro a leitura, especificamente da seção 4.6, sobre o processo de compensação por meio do lugar das raízes. Neste capítulo, é mostrado exemplos de controladores compensadores nas mais diversas situações práticas.
Disponível na Minha Biblioteca.
Caro estudante, chegamos ao final dos nossos estudos. Todavia, tenho certeza de que você deve estar refletindo a respeito dos usos dos software e do desenvolvimento de algoritmos — fundamentais para o projeto de um controlador PID, juntamente com o método de representação do Lugar Geométrico das Raízes e o Diagrama de Bode, tendo, inclusive, ideias de projetos na prática. Além disso, ao longo da nossa aprendizagem, foi possível perceber o quanto estas formas de representação já auxiliam, por si só, no entendimento do sistema físico real representado, respondendo antes mesmo de utilizarmos um controlador. Ademais, outra facilidade, que também foi possível perceber, é que através do lugar geométrico das raízes e do Diagrama de Bode podemos visualizar possíveis especificações para o sistema de controle e, assim, buscar atendê-las no controlador projetado. Espero que você tenha conseguido obter uma visão prática acerca destas diferentes técnicas, propondo-se a projetar um sistema de controle.
Até mais!
CASTRUCCI, P. L.; BITTAR, A.; SALES, R. M. Controle Automático. Rio de Janeiro: Editora LTC, 2018. (Disponível na Minha Biblioteca).
DORF, R. C. Sistemas de controle moderno. 13. ed. Rio de Janeiro: LTC, 2018.
FRANCHI, C. M. Controle de processos industriais: princípios e aplicações. São Paulo: Editora Ética, 2011. (Disponível na Biblioteca Virtual).
IDENTIFICAÇÃO da resposta em frequência. [S. l.: s. n.], 2020. 1 vídeo (20m). Publicado pelo canal Luís Antônio Aguirre. Disponível em: https://www.youtube.com/watch?v=ouuQRtHph3A. Acesso em: 05 abr. 2022.
NISE, N. S. Engenharia de sistemas de controle. 7. ed. Rio de Janeiro: LTC, 2018.
OGATA, K. Engenharia de controle moderno. 5. ed. São Paulo: Pearson Prentice Hall, 2010. (Disponível na Biblioteca Virtual).
PROJETO LR: controlador PID. [S. l.: s. n.], 2022. 1 vídeo (20m). Publicado pelo canal Luís Antônio Aguirre. Disponível em: https://www.youtube.com/watch?v=OGLD_nBk0ro. Acesso em: 05 abr. 2022.