Elementos de Máquinas
Introdução aos Elementos de Máquinas e Detalhamento dos Elementos de Transmissão
Tempo de leitura do conteúdo estimado em 1 hora e 48 minutos.
Olá, prezado(a) estudante! Você se lembra de quando era criança e ganhava aquele brinquedo com vários mecanismos? Você não resistia e logo o abria para ver como era por dentro, não é mesmo? Hoje você cresceu, e os “brinquedos” também, mas a curiosidade continua a mesma. Quando falo aqui de “brinquedos” que cresceram, estou me referindo a máquinas e equipamentos. Você sabe de que eles são compostos? São compostos de elementos de máquinas .
Nesta unidade, vamos conhecer os tipos de elementos de máquinas e entrar mais em detalhes nos elementos de transmissão. Será que você sabe a classificação dos elementos? Entende bem os elementos de transmissão? Vamos conhecê-los?
fundamentais
Neste tópico, vamos aprender um pouco mais sobre os elementos de máquinas. Vamos mostrar como estão divididos e quais as características em comum. Além disso, vamos tratar de alguns conceitos físicos que serão muito importantes para o dimensionamento dos elementos.
Os elementos de máquina estão divididos em “famílias”, em que a característica de uso é a que mais se destaca. Por exemplo, um parafuso está na “família” dos elementos de fixação, pois a função principal dele é fixar e prender outros componentes.
Para ilustrar melhor a divisão dos elementos em suas respectivas famílias, convido você para analisar a figura a seguir:
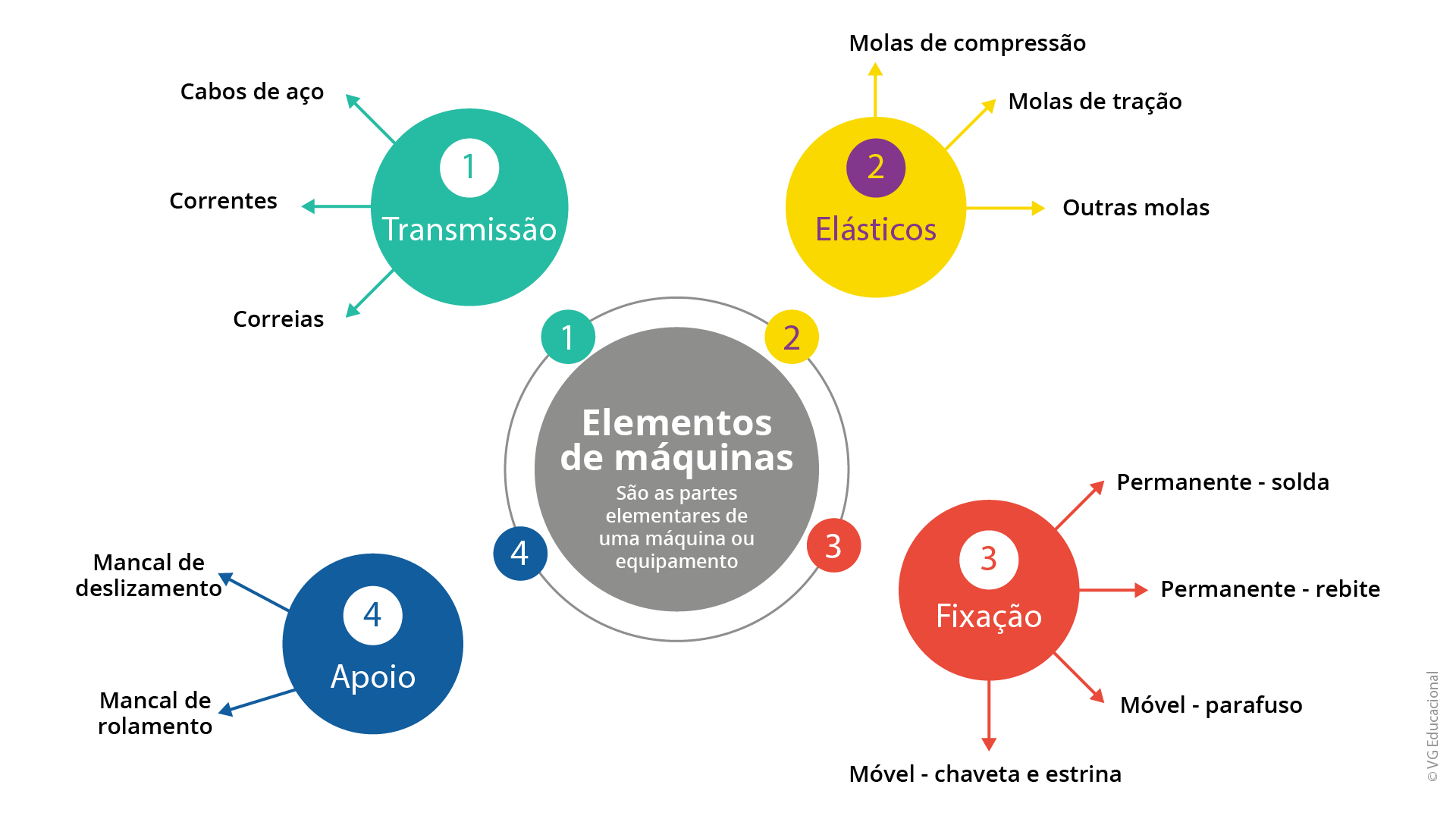
Fonte: Elaborada pela autora (2021).
#PraCegoVer : a imagem é formada por um círculo cinza no meio, no qual está escrito: “Elementos de máquinas - São as partes elementares de uma máquina ou um equipamento”. O círculo central está direcionado para quatro círculos menores. O círculo 1, em vermelho-escuro, contém o texto “Transmissão”, e dele saem três setas, com os textos “cabos de aço”, “correntes” e “correias”. No círculo 2, em amarelo-escuro, está escrito “Elásticos”, e dele saem três setas, em que está escrito: “molas de compressão”, “molas de tração” e “outras molas”. O círculo 3, em cor-de-rosa, contém o texto “Fixação”, e dele saem quatro setas, em que está escrito “Permanente - Solda”, “Permanente - rebite”, “Móvel - parafusos” e “Móvel - chaveta e estria”. No círculo 4, em azul, está escrito “Apoio”, e dele saem duas setas nas quais está escrito “mancal de deslizamento” e “mancal de rolamento”.
Certa vez, um motorista estava numa estrada, quando percebeu que uma luz se acendeu no painel, e seu carro parou. Por sorte, naquele momento, estava passando um mecânico que, notando o desespero do motorista, parou para ver o que estava ocorrendo. Você sabe o que aconteceu? A correia do alternador tinha arrebentado. Como o motorista não tinha uma correia sobressalente, o carro precisou ser rebocado. Essa história ilustra a importância da correia como um elemento de transmissão de movimento. Ela transmite o movimento do motor para o alternador.
SAIBA MAIS
Você sabe calcular a rotação das polias acionadas por uma correia? O vídeo mostra o passo a passo de uma transmissão por correia e polia, em que a polia motora trabalha a 1.600 rpm e tem diâmetro de 3.1/2", e a polia movida tem diâmetro de 6". O vídeo vai mostrar, nessas condições, como calcular a rotação da polia movida.
Principais elementos de máquinas
Os elementos de máquinas estão distribuídos em famílias, e podemos dividi-los em:
- Elementos de transmissão flexíveis : correias, correntes e cabos de aço;
- Elementos elásticos : molas de compressão, molas de tração e molas de torção;
- Elementos de fixação : permanente (solda e rebite) e móvel (parafusos, chavetas e estrias);
- Elementos de apoio : mancais de deslizamento e mancais de rolamento.
Os elementos de transmissão podem ser divididos em flexíveis e por engrenagens (que não serão abordadas neste curso). Os elementos de transmissão flexíveis englobam as correias, as correntes e os cabos de aço.
As correias trabalham em conjunto com as polias, enquanto as correntes trabalham em conjunto com rodas dentadas (MOTT, 2015). Vamos pensar em uma aplicação para a correia? Você se lembra do exemplo do alternador? Então, essa é uma das aplicações. E uma aplicação para a corrente? Você já andou de bicicleta? Se sim, certamente a corrente dela já quebrou ou saiu do lugar, não é mesmo? E os cabos de aço? Onde estão presentes? Você já andou de elevador? Então aí está um bom exemplo de uso de cabos de aço. A Figura 1.2 mostra uma aplicação combinada de correia, corrente e engrenagem.
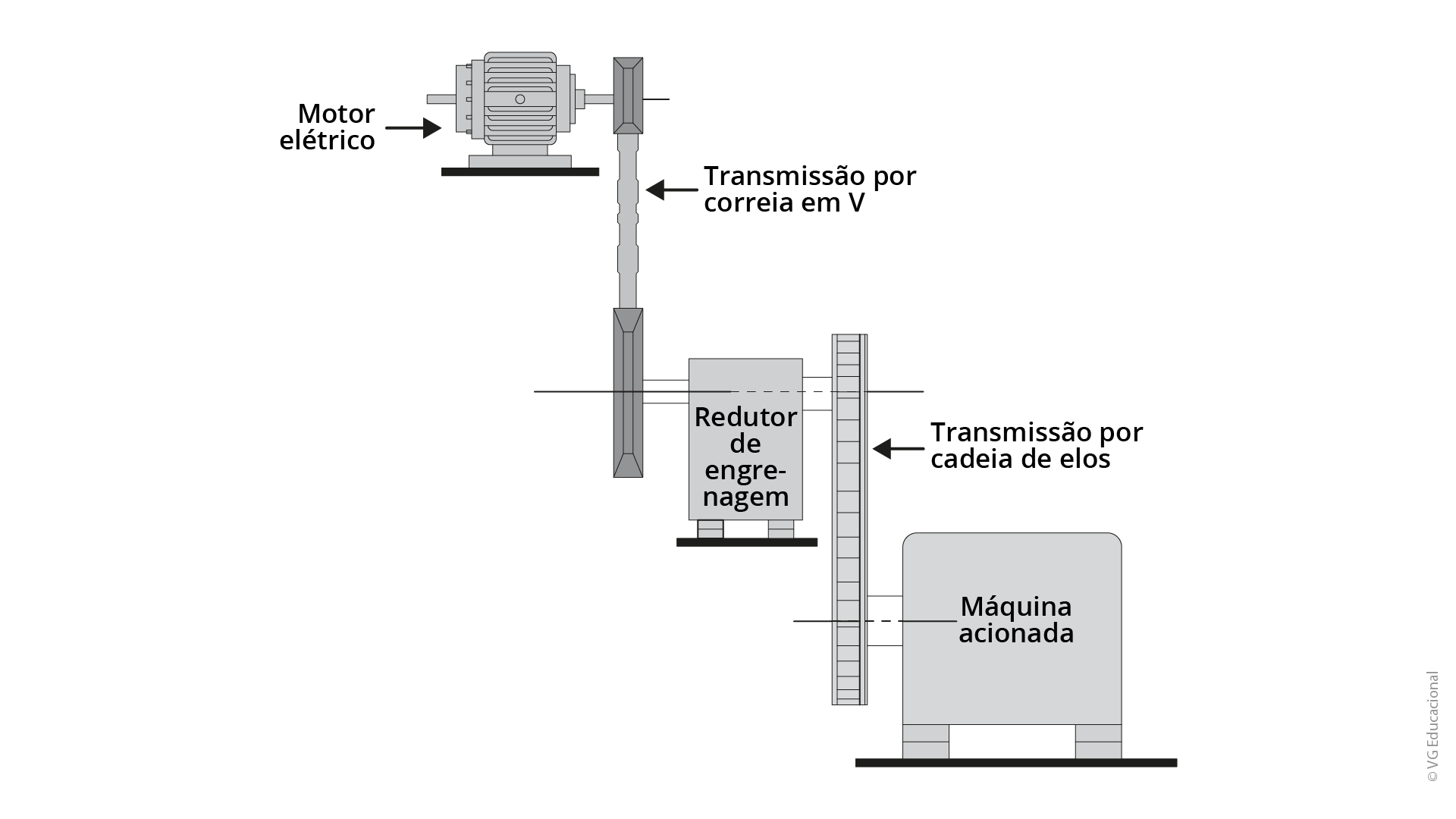
Fonte: Mott (2015, p. 278).
#PraCegoVer : a figura mostra um sistema de transmissão composto por um motor elétrico, que aciona um redutor de velocidade por meio de uma correia em V. O redutor está conectado a uma máquina por meio de uma transmissão por cadeia de elos.
Os elementos elásticos são representados pelas molas. Elas têm a função de armazenar energia e absorver ou amortecer choques e vibrações (FRANCESCHI; ANTONELLO, 2014). Agora vamos pensar numa aplicação de molas? Sabe aquele brinquedo em que um palhaço pula de dentro de uma caixa? Quando comprimimos a mola e guardamos o palhaço na caixa, exercemos uma força sobre a mola e fornecemos potência a ela. Quando a tampa é aberta, a força da mola faz o palhaço ser lançado para fora da caixa, e é aí que está a graça da brincadeira (MOTT, 2015).
As molas podem ser de compressão, de tração ou de torção. As molas de compressão possuem espiras, e, quando comprimidas, o espaço entre elas fica reduzido. As molas de tração , além das espiras, têm olhais para que possam exercer sua função, ou seja, para que possam ser esticadas (tracionadas). Já as molas de torção , além das espiras, têm braços de alavanca, pois, por meio deles, é possível a aplicação da torção.
SAIBA MAIS
O vídeo mostra as molas japonesas, que são conhecidas pela precisão e pelo alto desempenho, incluindo uma mola minúscula na ponta da caneta esferográfica. O Japão pode produzir molas minúsculas, que podem ser usadas como stents , passando dentro de vasos sanguíneos do cérebro. O vídeo também mostra uma grande mola que fica no topo de uma torre em Tóquio.
Quando falamos de fixação , precisamos pensar: o que vai ser fixado precisa ser solto em algum momento? A fixação deve ser permanente ou móvel? Mas o que é uma fixação permanente? Aqui estamos falando de soldas e rebites, em que dois metais são unidos de forma permanente. A eliminação da fixação causará destruição da peça ou da união (FRANCESCHI; ANTONELLO, 2014). Em algumas aplicações, isso é até interessante, mas, em outras, precisamos pensar em separar os componentes sem destruir as peças. Para essa situação, temos a fixação móvel, por meio de parafusos e porcas.
Agora pense em uma aplicação dos parafusos. Essa está fácil, não é mesmo? Podemos citar uma infinidade de aplicações, basta olharmos à nossa volta. Outro ponto que deve ser observado é que, “no projeto de máquinas, a maioria dos elementos de fixação é feita de aço por causa da alta resistência, da rigidez elevada e da boa ductilidade, usinabilidade e maleabilidade” (MOTT, 2015, p. 732).
Os parafusos são classificados pelo tipo de material, tipo de rosca, tamanho do parafuso e tipo da cabeça. Precisamos nos aprofundar mais nesse assunto, concorda? A figura a seguir apresenta um conjunto de tipos distintos de parafusos.

Fonte: Pixabay.
#PraCegoVer : a figura tem o fundo branco e, da esquerda para a direita, mostra cinco parafusos arrumados em leque. O parafuso mais à esquerda tem a cabeça chata; o segundo tem a cabeça redonda; o do meio tem um tamanho maior que os demais e tem a cabeça chata; em seguida, um parafuso de cabeça chata com fenda; e, finalmente, um de cabeça redonda com fenda.
Os elementos de apoio são os mancais, as buchas e as guias. Os mancais podem ser de deslizamento ou de rolamento.
A função dos mancais é minimizar o atrito e, portanto, aumentar o rendimento do sistema mecânico, entre partes que se movem entre si. A aplicação dos mancais pode ser observada na relação entre eixos e carcaças de redutores e entre carros e barramentos de máquinas-ferramentas (FRANCESCHI; ANTONELLO, 2014, p. 43).
Nos mancais de deslizamento, as partes envolvidas estão em contato direto uma com a outra, e, para reduzir o atrito entre elas, a lubrificação é fundamental. O estudo da lubrificação abrange conhecimentos de química, termodinâmica, transferência de calor e mecânica dos fluidos (BUDYNAS; NISBETT, 2016). Mas não se assustem, pois nem todos esses conceitos serão abordados no nosso curso.
Já os mancais de rolamento são utilizados para permitir o movimento relativo entre dois elementos, além de sustentar uma carga. Seus elementos rolantes podem ser esferas, cilindros ou roletes cônicos (MOTT, 2015).
Conceitos de torção e movimento circular
Para a correta aplicação e seleção do elemento de máquina que será escolhido para determinada aplicação, é preciso desenvolver alguns cálculos. Os cálculos mais complexos podem ser executados com o auxílio de métodos computacionais. Para entender o que a planilha eletrônica ou o programa de computador está solicitando, precisamos saber fazer os cálculos necessários (MOTT, 2015).
Para chegarmos aos cálculos específicos para cada tipo de elemento de máquina, primeiro vamos entender alguns conceitos fundamentais, tais como o movimento circular e a torção. Isso porque quase todas as máquinas e equipamentos, compostos de elementos de máquinas, sofrerão uma dessas solicitações ou ambas.
Você sabe o que caracteriza o movimento circular ? O movimento circular é aquele em que uma partícula executa uma trajetória circular de raio r e tem determinado deslocamento angular em determinado tempo. Os parâmetros a serem considerados no movimento circular são: i) velocidade angular; ii) período; iii) frequência; iv) rotação; e v) velocidade tangencial (MELCONIAN, 2019).
Consideremos uma partícula P que se desloca do ponto \(P_1\) num tempo \(t_1\) para o ponto \(P_2\) num tempo \(t_2\) conforme mostra a Figura 1.4.
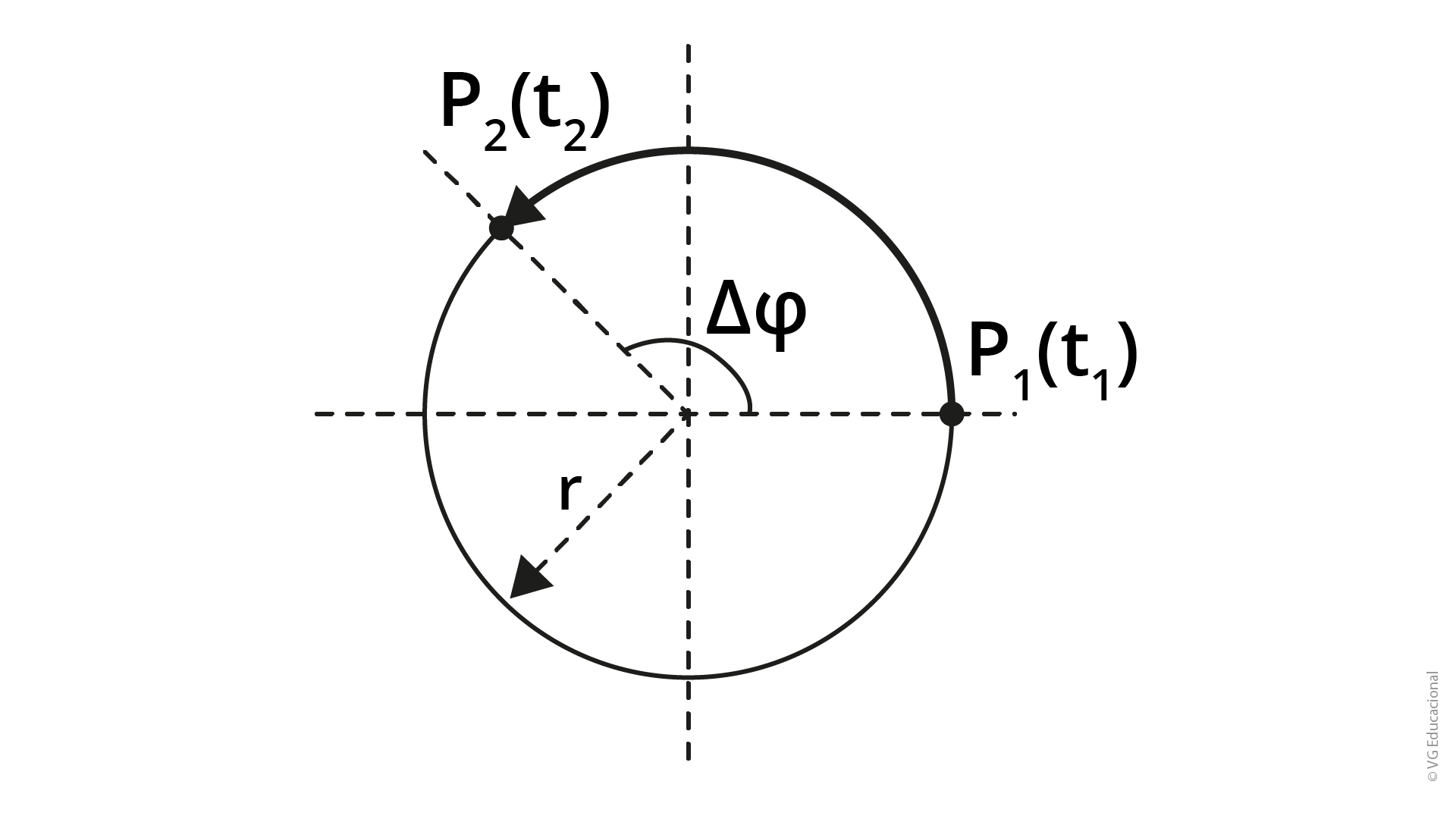
Fonte: Melconian (2019, p. 11).
#PraCegoVer : a figura é um círculo de raio r com uma partícula P partindo do ângulo 0° até o ângulo de 90°. Na posição inicial (0°), está indicada a posição P1(t1), e, na posição final (90°), está indicada a posição P2(t2). Entre as posições iniciais e finais, está indicado o ângulo 𝛥𝜑.
I. A velocidade angular é dada pela relação entre a variação angular e a variação do tempo:
\[ω=\frac{Δφ}{Δt}~(Equação~1)\]
Em que:
𝜔 = velocidade angular [rad/s];
𝛥𝛗 = variação angular [rad];
𝛥t = variação do tempo [s].
II. O período é o tempo necessário para que a partícula complete uma volta no movimento circular. Sabe-se que o círculo tem um perímetro de 2𝜋 rad, então o período é dado por:
\[T = \frac{2π}{ω}~(Equação~2)\]
Em que:
T = período [s];
𝜋 = constante trigonométrica (3,1415…);
𝜔 = velocidade angular [rad/s].
III. A frequência é o inverso do período e representa o número de ciclos que a partícula descreve em um movimento circular durante um segundo. É dada por:
\[f=\frac{1}{T}=\frac{ω}{2π}~(Equação~3)\]
Em que:
f = frequência [Hz];
T = período [s];
𝜔 = velocidade angular [rad/s];
𝜋 = constante trigonométrica (3,1415…).
IV. A rotação é o número de ciclos que uma partícula em movimento circular faz em um minuto. Como a frequência é em segundos e a rotação em minutos, temos que:
\[n = 60.f ⇒ como~f=\frac{ω}{2π}, então~n =\frac{60.ω}{2π}\]
Reduzindo, temos:
\[n =\frac{30.ω}{π}~(Eq.4)\]
Em que:
n = rotações [rpm];
𝜔 = velocidade angular [rad/s];
𝜋 = constante trigonométrica (3,1415…).
V. A velocidade tangenci al é sempre tangente ao movimento. Ela muda de direção a cada instante, mas seu módulo é constante. A Figura 1.5 apresenta a representação de velocidades tangenciais.
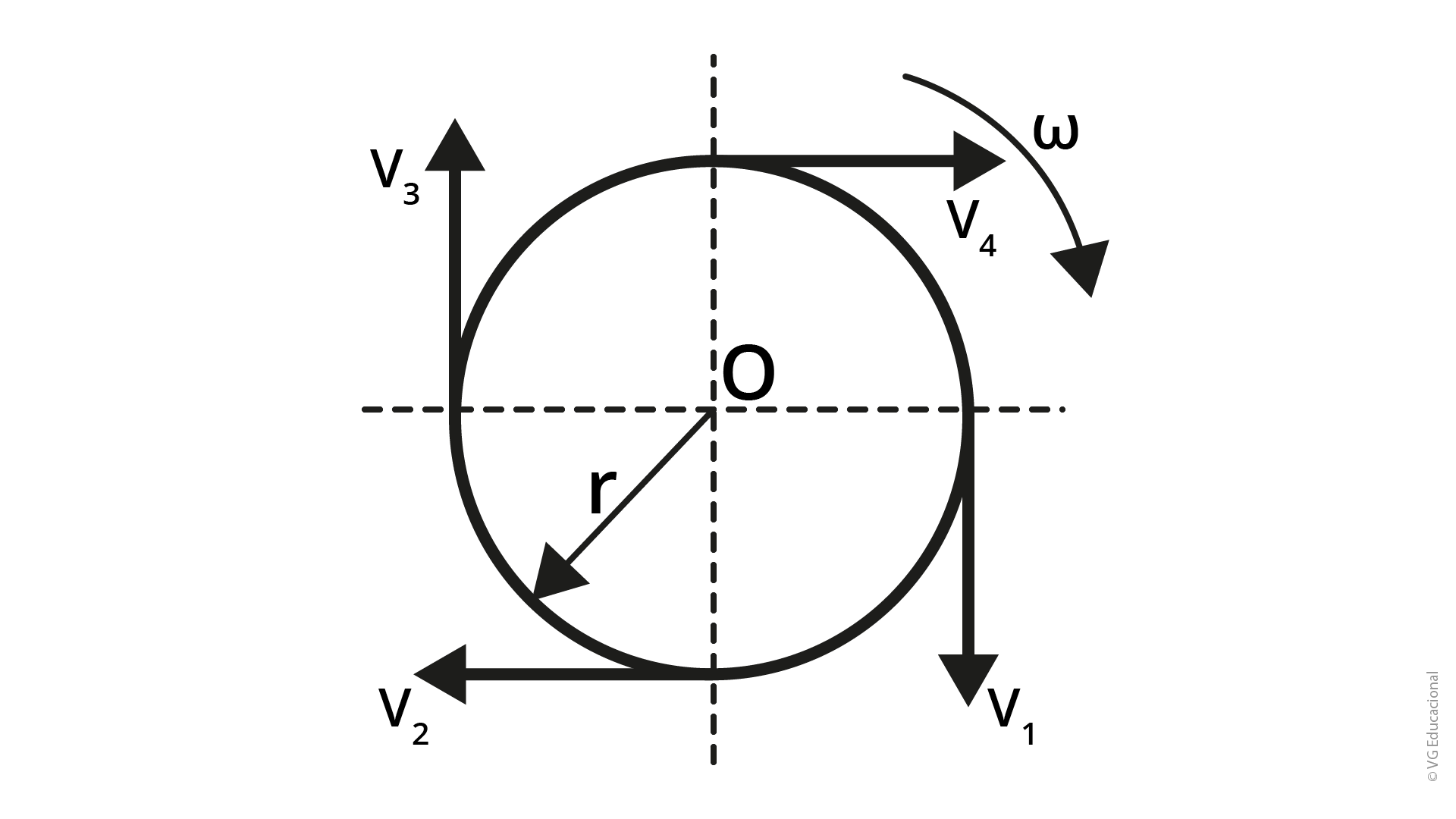
Fonte: Melconian (2019, p. 12).
#PraCegoVer : a figura mostra um círculo de raio r e origem em 0. Nas quatro extremidades do círculo, estão representadas as direções dos vetores de velocidade. No ângulo 0°, o vetor v1 está direcionado para baixo; no ângulo de 270°, o vetor v2 está direcionado para a esquerda; no ângulo de 180°, o vetor v3 está direcionado para cima; e, no ângulo de 90°, o vetor v4 está direcionado para a esquerda. Entre os ângulos 90° e 0°, há uma seta curva, orientada de cima para baixo, e acima da seta, a indicação do símbolo da velocidade angular (𝜔).
A relação entre a velocidade tangencial e a velocidade angular está no raio do movimento circular, em que:
\[\frac{v}{ω}=r ⇒ v = ω.r~(Equação~5)\]
Isolando a velocidade angular na equação 4, temos \(ω = \frac{π.n}{30}\) e substituindo na equação 5, temos:
\[v =\frac{π.n}{30}.r~(Equação~6)\]
Em que:
v = velocidade tangencial [m/s];
r = raio [m];
n = rotação [rpm];
𝜋 = constante trigonométrica (3,1415…).
Vamos ver a aplicação das equações?
Exemplo 1 (MELCONIAN, 2019, p. 14)
Um motor elétrico possui a rotação de 1.740 rpm. Determine as seguintes características do motor:
a) velocidade angular;
b) período;
c) frequência.
Solução :
a) velocidade angular (𝜔)
No problema, foi dada a rotação n = 1.740 rpm.
Para acharmos a velocidade angular, vamos usar a equação 4 da rotação, dada por \(n =\frac{30.ω}{π}\). Substituindo os valores, temos \(1740 =\frac{30.ω}{π}\) e, isolando a velocidade angular, temos
\(ω=\frac{1740.π}{30}\). Logo, 𝜔 = 58𝜋 rad/s .
b) período (T)
O período é definido pela equação 2 e é dado por \(T =\frac{2π}{ω}\). Substituindo a velocidade angular, temos \(T =\frac{2.π}{58.π}\), que resulta em: \(T =\frac{1}{29}\), T = 0,034 s .
c) frequência (f)
A frequência é o inverso do período. Então, \(f= \frac{1}{\frac{1}{29}}\), f = 29 Hz .
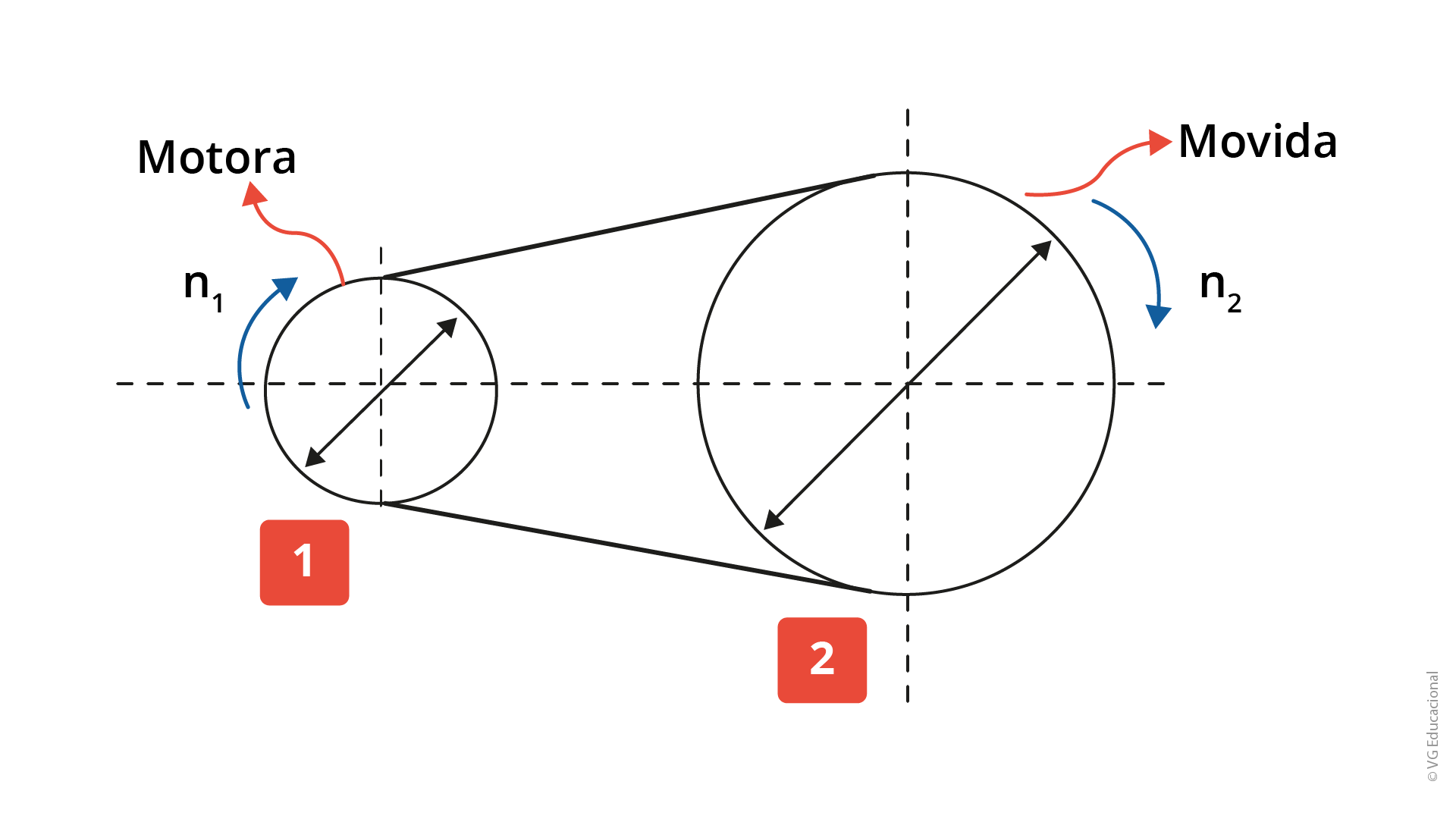
Sabendo as relações entre frequência, período, rotação e velocidade angular, vamos conhecer as relações de transmissão de correias. Na Figura 1.6, são dadas as duas condições de transmissão por correia, a transmissão redutora de velocidade e a transmissão ampliadora de velocidade.
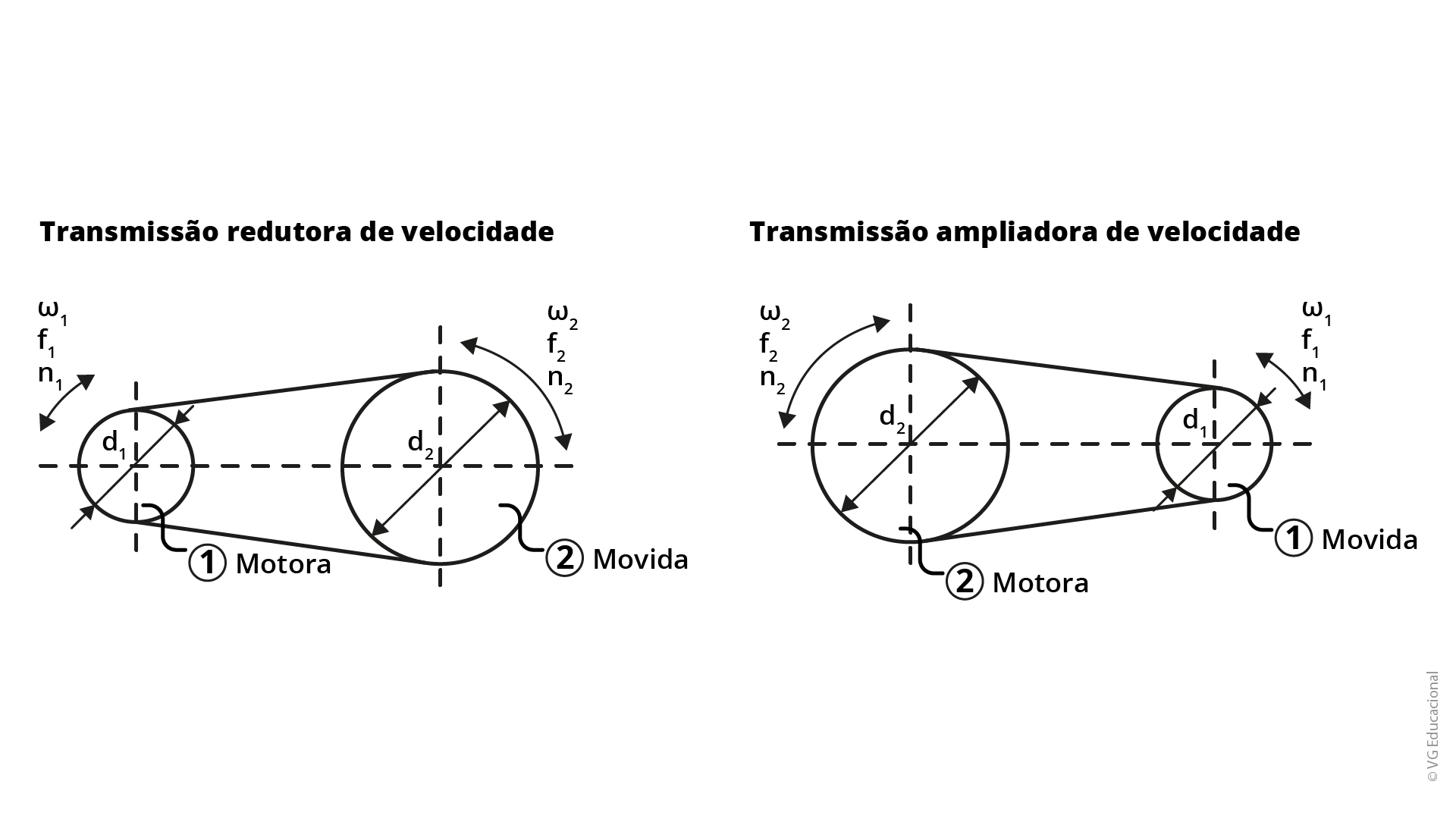
Fonte: Melconian (2019, p. 14).
#PraCegoVer : a figura mostra duas transmissões por correias. No lado esquerdo, está a transmissão redutora de velocidade, em que, mais à esquerda, está a polia menor (motora), de diâmetro d1, e, mais à direita, a polia maior (movida), de diâmetro d2. Em cada polia, estão representadas as indicações de rotação (n), frequência (f) e velocidade angular (𝜔). No lado direito, está a transmissão ampliadora de velocidade, em que mais à esquerda está a polia maior (motora), de diâmetro d2, e mais à direita, a polia menor (movida), de diâmetro d1. Em cada polia, estão representadas as indicações de rotação (n), frequência (f) e velocidade angular (𝜔).
A relação de transmissão é dada por:
\[i = \frac{d_2}{d_1} =\frac{ω_1}{ω_2} =\frac{f_1}{f_2} =\frac{n_1}{n_2} =\frac{M_{T1}}{M_{T2}} (Equação~7)\]
Em que: i é a relação de transmissão [adimensional] e as demais relações estão representadas no Quadro 1.1
Fonte: Adaptado de Melconian (2019).
#PraCegoVer : o quadro tem seis colunas e três linhas. Na primeira linha: Vazia, Diâmetro [m…], Velocidade angular [rad/s], Frequência [Hz], Rotação [rpm] e Torque [N.m]. Na segunda linha: Polia 1, \(d_1\) (menor), \(𝜔_1\), \(f_1\), \(n_1\) e \(M_{T1}\). Na terceira linha: Polia 2, \(d_2\) (maior), \(𝜔_2\), \(f_2\), \(n_2\) e \(M_{T2}\).
Vimos até aqui as características do movimento circular, que relaciona os parâmetros de velocidade angular, período, frequência, raio, rotação e velocidade tangencial. Lembre-se bem desses conceitos, pois serão utilizados mais adiante!
Movimento circular
O que é velocidade angular?
Abertura da faixa: É a relação entre a variação angular e a variação do tempo: \(ω=\frac{Δφ}{Δt}\).
O que é período?
Abertura da faixa: É o tempo necessário para que a partícula complete uma volta no movimento circular: \(T =\frac{2π}{ω}\).
O que é frequência?
Abertura da faixa: É o inverso do período e representa o número de ciclos que a partícula descreve em um movimento circular durante um segundo: \(f=\frac{1}{T}=\frac{ω}{2π}\).
O que é rotação?
Abertura da faixa: É o número de ciclos que uma partícula em movimento circular faz em um minuto: \(n =\frac{30.ω}{π}\).
O que é velocidade tangencial?
Abertura da faixa: A relação entre a velocidade tangencial e a velocidade angular está no raio do movimento circular: \(v =\frac{π.n}{30}.r\)
- conteúdo do item 1: Eu mi bibendum neque egestas congue quisque egestas diam in.
- conteúdo do item 2: Eu mi bibendum neque egestas congue quisque egestas diam in.
- conteúdo do item 3: Eu mi bibendum neque egestas congue quisque egestas diam in.
Já vimos o movimento circular, agora vamos conhecer um pouco sobre a torção. Você sabe quando uma peça está sob torção? O esforço de torção ocorre quando uma peça sofre um torque em uma extremidade e um contra-torque na extremidade oposta, como mostrado na Figura 1.7 (MELCONIAN, 2019).
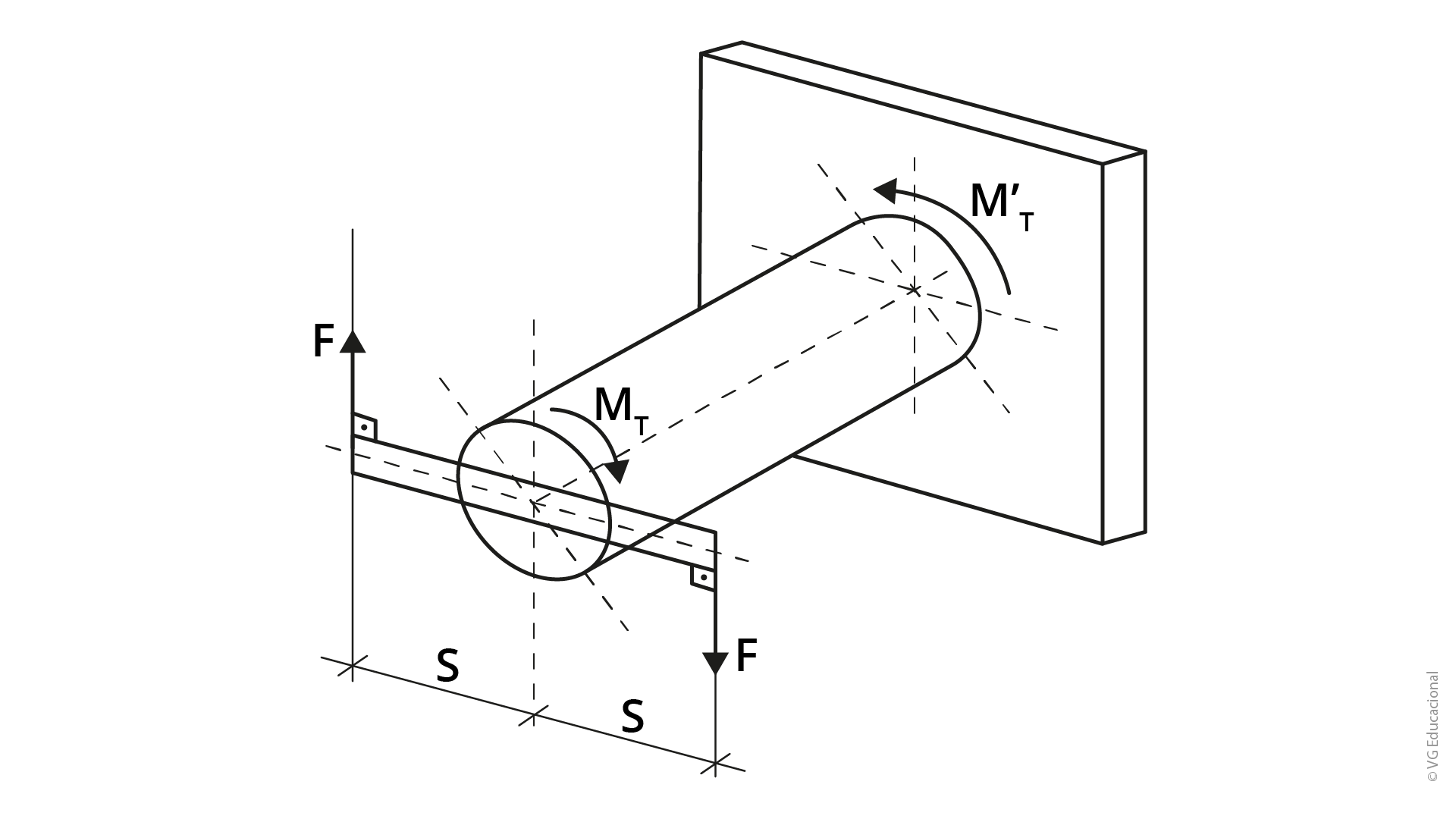
Fonte: Melconian (2019, p. 21).
#PraCegoVer : a figura mostra, em 3D, um eixo cilíndrico engastado numa peça quadrada. Na interseção entre o eixo e a peça quadrada, está representado o torque direcional da direita para a esquerda, no valor M’T. Na outra extremidade do eixo, há um retângulo paralelo ao quadrado do engaste, no qual está representado o binário de forças F nas extremidades do retângulo, sendo que mais à esquerda da figura o vetor F está direcionado para cima, e, mais à direita, direcionado para baixo. Na extremidade circular do eixo, está representado o torque MT, direcionado da esquerda para a direita.
Para as transmissões mecânicas, algumas relações devem ser definidas, entre as quais estão o torque (\(M_T)\), a potência (P), a relação torque X potência e a força tangencial (FT). O Quadro 1.2, a seguir, apresenta as referidas equações, em que o raio é representado por r, a velocidade angular por 𝜔, a rotação por n e a velocidade tangencial por \(v_p\).
Fonte: Elaborado pela autora (2021).
#PraCegoVer : o quadro tem cinco colunas e quatro linhas. A primeira coluna está preenchida com os parâmetros: equação, símbolo da unidade e unidade. A segunda coluna contém informações sobre o torque (MT): a equação\( M_T=F_T.r\), o símbolo da unidade [N.m] e a unidade Newton metro. A terceira coluna contém as informações da Potência (P): a equação \(P = F_T.v_P\), o símbolo da unidade [Nm/s = J/s = W] e a unidade Watts. A quarta coluna está preenchida com os elementos do torque X potência: a equação \(M_T=\frac{30}{π}.\frac{P}{n}\), o símbolo da unidade [N.m] e a unidade Newton metro. A quinta e última coluna contém os elementos da força tangencial \(F_T\): a equação \(F_T=\frac{M_T}{r}=\frac{P}{v_p} =\frac{P}{(ω.r)}\), o símbolo da unidade [N] e a unidade Newton.
A transmissão por correia representada na figura 1.8 é acionada por um motor elétrico com potência P = 4,5 kW e rotação de 1.750 rpm. Sabe-se que a polia 1 é a polia motora do sistema e tem 100 mm de diâmetro e que a polia 2 tem 250 mm de diâmetro.
MELCONIAN, S. Elementos de máquinas . 11. ed. São Paulo: Érica, 2019.
Desprezando as perdas, os valores aproximados do torque da polia 1 e da velocidade angular da polia 2 são, respectivamente, iguais a:
Prezado(a) estudante, quando falamos de transmissão por correia, qual aplicação vem primeiro à sua mente? Eu penso logo no motor do carro. Mas por quê? Bem, o motor tem um sistema de transmissão por correia, que interliga o motor, o alternador e a bomba de água, como pode ser visto na Figura 1.8, na qual, à esquerda, está a foto do motor, e à direita, a representação da transmissão. Vamos entender isso melhor?

Fonte: Melconian (2019, p. 16).
#PraCegoVer : Na esquerda, tem uma foto colorida da lateral do motor de combustão interna. À esquerda, na parte superior da foto, está a polia da bomba de água em cinza escuro. No meio da foto, tem duas polias: uma superior, na cor cinza, com quatro furos, e uma inferior, na cor laranja, que é o volante do motor. Mais à direita da foto, está a polia do alternador e, acima, uma polia menor. Na direita, há um desenho representando as três polias da foto, formando um triângulo. À esquerda superior do desenho, está a polia menor, representando o alternador; no meio, mais abaixo, está a polia maior, representando o volante do motor; e, mais à direita, está a polia de tamanho intermediário, representando a bomba de água.
No próximo tópico, vamos falar sobre as correias, seus tipos, suas aplicações, além do dimensionamento e da seleção. Vamos lá?
Principais tipos de correias e aplicações
Quando comparamos a transmissão por correia com as transmissões por corrente ou por engrenagens, podemos elencar algumas vantagens e desvantagens, como mostrado no Quadro 1.3.
Fonte: Adaptado de Niemann (1971b, p. 87).
#PraCegoVer : o quadro contém sete vantagens e cinco desvantagens das correias. As vantagens são: pouco ruído; absorção e amortecimento de choques; disposição simples; utilização múltipla (cruzada, inclinada, vários eixos etc.); mais economia, por conta da simplicidade; desacoplamento fácil; simples variação da relação de multiplicação. As desvantagens são: maiores dimensões e maior força axial; maior escorregamento na transmissão de força; alongamento da correia, que aumenta com o tempo de uso; variação do alongamento com a temperatura e a umidade; variação do coeficiente de atrito, com poeira, detritos, óleo e umidade.
Existem vários tipos de correias, como as planas, as correias em V, as correias em duplo V, com ranhuras e dentadas, entre outras (MOTT, 2015).
Tendo em mente os diversos tipos de correias que foram citadas, verifique a Figura 1.9, a seguir, que mostra alguns deles.
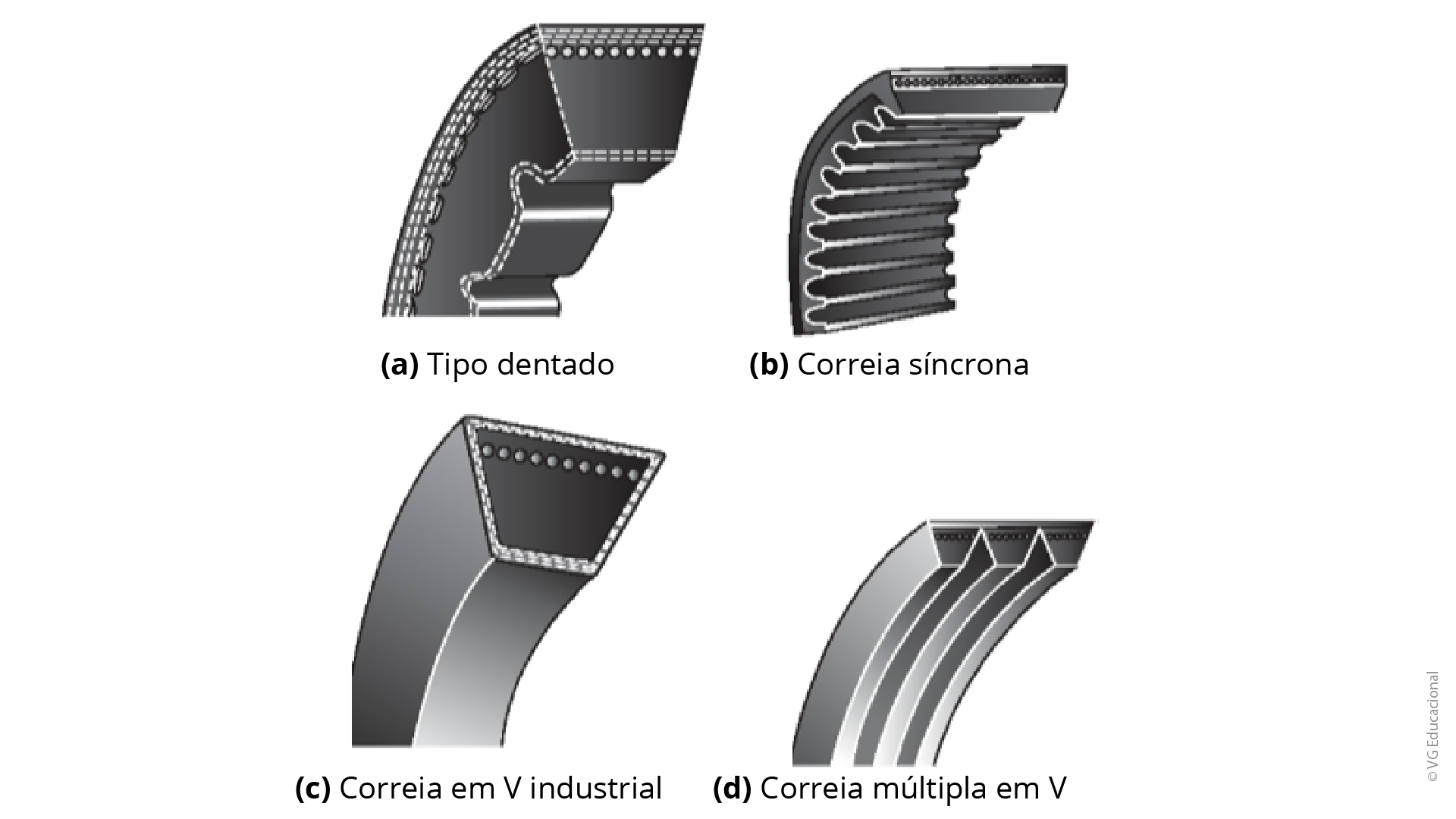
Fonte: Mott (2015, p. 280).
#PraCegoVer : figura com fundo branco, com duas linhas e duas colunas. A primeira figura da linha superior à esquerda, marcada com a letra a), é a figura em corte de uma correia dentada. A figura ao lado dessa está indicada pela letra b) e é o desenho em corte de uma correia síncrona. Na parte inferior da figura, no lado esquerdo, está o desenho em corte de uma correia em V industrial, marcada com a letra c). Ao seu lado, está o desenho da correia múltipla em V, marcada com a letra d).
As correias do tipo dentadas (a) e síncronas (b) são utilizadas em polias com ranhuras em V padrão. As correias em V industrial (c) e múltipla em V (d) têm perfil em V, que deixa a correia bem apertada dentro da ranhura da polia, o que faz com que torques elevados sejam transmitidos sem a correia deslizar.
Fonte: Hebert Santos / Pexels.
Correias dentadas
A correia dentada é muito utilizada nas transmissões veiculares, e sua grande vantagem é não ter nenhum deslizamento. Como desvantagem dessa aplicação, está o fato de que a correia, por ser fabricada em borracha, está sujeita a perder eficiência devido ao aquecimento.
Fonte: Andrea Piacquadio / Pexels.
Correias planas
As correias planas têm ampla utilização, podendo ser usadas também para transporte de cargas, em esteiras de exercícios e em diversas outras aplicações. A versatilidade desse tipo de correia está na possibilidade de emendá-las, o que torna possível sua aplicação em distâncias relativamente longas. Outra vantagem é o uso como embreagem, já que a correia permite deslizamento.
As correias trabalham em conjunto com as polias, e estas devem acompanhar a geometria daquelas. Por exemplo, a correia em V mostrada em (a), na Figura 1.10, é muito utilizada na indústria e em aplicações veiculares.
As correias em V são padronizadas. O Quadro 1.4 mostra a especificação delas.
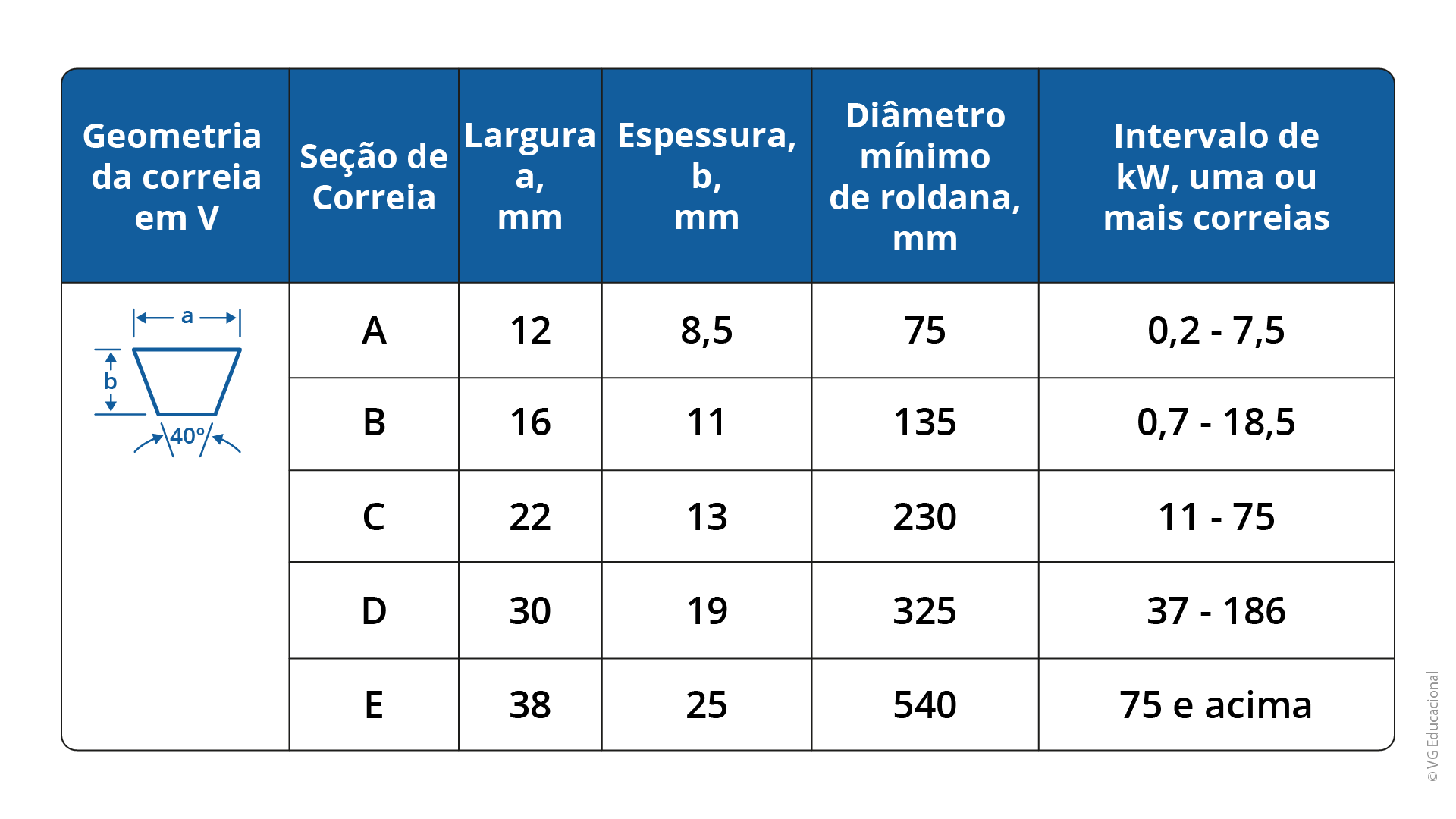
Fonte: Adaptado de Budynas e Nisbett (2016).
#PraCegoVer : quadro com seis linhas e seis colunas. A primeira coluna mostra o desenho da geometria da correia em V, representada por um trapézio cuja largura é medida pela letra “a” e a altura pela letra “b”. A segunda coluna apresenta os tipos de correia, de acordo com as medidas “a” e “b”, e são representadas pelas letras A, B, C, D e E. Nas demais colunas, estão os respectivos valores da largura “a”, em mm, da altura “b”, em mm, do diâmetro da roldana, em mm, e do intervalo de kW em uma ou mais correias. Os valores são assim distribuídos. Na linha 2: A; 12; 8,5; 75; 0,2–0,75. Na linha 3: B; 16; 11; 135; 0,7–18,5. Na linha 4: C; 22; 13; 230; 11–75. Na linha 5: D; 30; 19; 325; 37–186. Na linha 6: E; 38; 25; 540; 75 e acima.
No próximo subtópico, será detalhado o dimensionamento das correias planas e das correias em V.
Dimensionamento e aplicação de correias e polias
Atualmente, as correias planas são fabricadas com um núcleo elástico impregnado com borracha e apresentam algumas vantagens sobre as transmissões por engrenagens ou por correias em V. Uma transmissão por correia plana pode chegar a 98% de eficiência, enquanto as transmissões por correia em V têm eficiência entre 70% a 96%. Outra vantagem das correias planas é o baixo ruído e a alta absorção das vibrações torcionais, sendo, nesse aspecto, mais eficientes que as transmissões por correia em V (MOTT, 2015).
As correias planas são podem trabalhar abertas ou cruzadas, e o dimensionamento abrange o cálculo do ângulo de contato ou abraçamento (𝜃) e o comprimento total da correia (L). A seguir, temos a Figura 1.11, que apresenta as configurações aberta (a) e cruzada (b). Vamos analisá-la para melhor compreensão desse conceito.
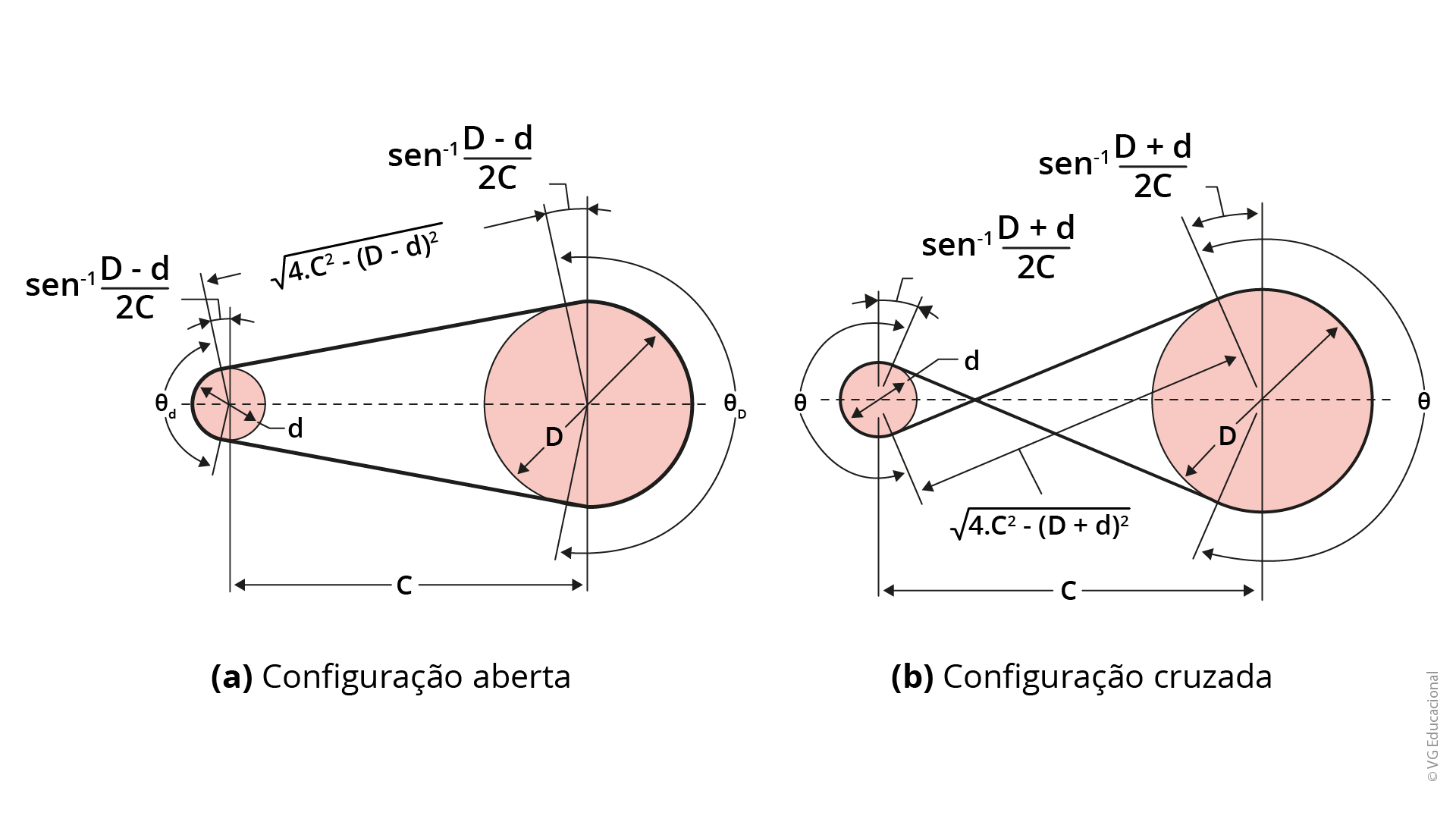
Fonte: Budynas e Nisbett (2016, p. 864).
#PraCegoVer : a figura mostra duas configurações das correias. No lado esquerdo, está a configuração aberta, marcada com a letra a), e, no lado direito, a configuração cruzada, marcada com a letra b). São apresentados alguns parâmetros das configurações.
Para as correias planas abertas (Fig. 1.11a), os ângulos 𝜃D e 𝜃d são dados por:
\[θ_D=π+2.sen^{-1}\frac{D - d}{2C}~(Equação~8)\]
\[θ_d=π-2.sen^{-1}\frac{D - d}{2C}~(Equação~9)\]
Em que:
D = diâmetro da polia maior;
d = diâmetro da polia menor;
C = distância entre centros;
𝜃 = ângulo de contato.
O comprimento da correia é dado pela soma dos dois arcos mais duas vezes a distância entre centros (C):
\[L =[4C^2-(D-d)^2 ]^{1/2}+\frac{1}{2}.(D.θ_D+d.θ_d )~(Equação~10)\]
Em que:
𝜃D= ângulo de contato da polia maior;
𝜃d = ângulo de contato da polia menor.
Para as correias planas cruzadas (Fig. 1.11b), o ângulo de contato, tanto para a polia maior quanto para a polia menor, é o mesmo e é definido por:
\[θ=π+2.sen^{-1}\frac{D + d}{2C}~(Equação~11)\]
O comprimento da correia é dado por:
\[L=\left [ 4C^2- (D+d)^2 \right ]^{1/2}+\frac{1}{2}\cdot(D+d.)\theta~(Equação 12)\]
As correias em V , ao contrário das correias planas, só podem trabalhar em árvores paralelas. Para o correto dimensionamento das correias em V, é preciso conhecer os seguintes dados: 1) tipo do motor; 2) potência do motor; 3) rotação do motor; 4) tipo de máquina ou equipamento; 5) rotação da máquina ou equipamento; 6) distância entre centros e 7) tempo de trabalho diário da máquina ou equipamento (MELCONIAN, 2019).
Prezado(a) estudante, para a realização dos cálculos e a seleção, são utilizadas equações, tabelas e gráficos. Para facilitar o entendimento, vamos ver o passo a passo.
1º passo : cálculo da potência projetada, de acordo com o tipo do motor e as condições de serviço:
\[P_p=P_{motor}.f_s(Equação~13)\]
Em que:
\(P_p\) = potência projetada [CV];
\(P_{motor}\) = potência do motor [CV];
\(f_s\) = fator de serviço tabelado que depende do tipo do motor, do tipo da máquina e da condição de trabalho [adimensional].
2º passo : seleção do perfil da correia.
A seleção do perfil pode ser pelo diâmetro mínimo da polia menor (dado no Quadro 1.4) ou por meio de gráficos disponibilizados pelos fabricantes, em que se entra com a potência projetada e a rotação máxima e seleciona-se o perfil da correia (A, B, C, D ou E).
3º passo : diâmetro das polias.
O diâmetro da polia motora está relacionado à potência projetada e à maior rotação, então consulta-se uma tabela do fabricante e verifica-se o menor diâmetro para a potência do motor e a maior rotação. Caso haja limitação para o tamanho de uma das polias, deve-se definir qual será a polia maior e a menor.
A relação entre os diâmetros das polias motora e movida é dada por:
\[d = D.\frac{n_1}{n_2}~(Equação~14)\]
Em que:
\(n_1\) = rotação da polia 1 [rpm];
\(n_2 \)= rotação da polia 2 [rpm].
4º passo : cálculo do comprimento da correia (L).
Geralmente atribui-se uma distância entre centros (C), conforme informado no problema ou conforme os dados da tabela. Com esse dado e com os diâmetros das polias, calcula-se o comprimento da correia:
\[L= 2C + 1,57(D + d) +\frac{D - d^2}{4C}~(Equação~15)\]
5º passo : ajuste do comprimento da correia.
As correias em V têm tamanhos padronizados por tabelas. Com o valor calculado, devemos entrar na tabela e encontrar o valor tabelado mais próximo, então é calculado o comprimento de ajuste da correia \((l_A)\):
\[l_A=l_C-1,57(D+d)~(Equação~16)\]
Em que:
\(l_A\) = ajuste do comprimento;
\(l_C\) = comprimento tabelado.
Com esse valor, então, calcula-se o fator de correção da distância entre centros (h), da seguinte forma:
\[\frac{D-d}{l_A}~(Equação~17)\]
Com esse valor, acessa-se a tabela 4.6 presente no livro de Melconian (2019, p. 59) e encontra-se o valor de h. Com o valor de h, é possível achar a distância entre centros ajustada (C(a)), em que:
\[C_{(a)}=\frac{l_A- h(D-d)}{2}~(Equação~18)\]
6º passo : capacidade de transmissão de potência por correia \((P_{pc})\).
A capacidade de potência é dada pelo produto da soma da potência básica (Pb) e da potência adicional (Pa) pelos fatores de correção de comprimento (\(f_{cc}\)) e de arco de contato (\(f_{cac}\)), em que:
\[P_{pc}=(P_b+P_a).f_{cc}.f_{cac}~(Equação 19)\]
Os valores das potências básica e adicional são encontrados nas tabelas 4.7 a 4.14 de Melconian (2019, p. 60 e 67), em que a potência básica é obtida pela rotação máxima e pelo diâmetro da polia, e a potência adicional é obtida pela relação de redução e pela rotação.
O \(f_{cc}\) é encontrado nas tabelas 4.15 e 4.16 de Melconian (2019, p. 68-69), entrando apenas com o modelo da correia (exemplo: \(A60\Rightarrow f_cc = 0,97\)). Para o cálculo do fcac, primeiro encontramos:
\[\frac{D-d}{C_{(a)}}~(Equação~20)\]
Então, na tabela 4.17 de Melconian (2019, p. 69), encontramos o fator de correção. Com todos os fatores, calculamos o \(P_{pc}\) da equação 19.
7º passo : cálculo do número de correias necessárias (\(n_{co}\)).
Com o valor do \(P_{pc}\), encontramos a relação:
\[n_{co}=\frac{P_p}{P_{pc}}~(Equação~21)\]
Em que: \(P_p\) é a potência projetada; e \(P_{pc}\) é a capacidade de transmissão de potência. Se o valor de \(n_{co}\) for maior que 1, então há necessidade de mais de uma correia, e o valor deve ser aproximado para maior (exemplo: se \(n_{co} = 1,6\), então são necessárias duas correias).
Podem, ainda, ser solicitados os cálculos do torque e da força tangencial, que já foram discutidos no tópico 1.1.2 desta unidade.
O cálculo da correia em V pode parecer um pouco complexo, mas é como se fosse uma receita de bolo: basta juntar os ingredientes, ver o modo de fazer, colocar para assar (pensar um pouco), e nosso bolo estará pronto!
Caro(a) estudante, imagine que você está passeando de bicicleta por uma ciclovia, então você pedala e a bicicleta não responde. Você sabe o que pode ter acontecido? A corrente pode ter desacoplado da roda dentada. Isso mesmo. As transmissões por corrente funcionam assim: uma corrente, também chamada de cadeia de elos, acoplada a uma roda dentada, transmite potência para uma máquina ou um equipamento.
Neste tópico, vamos conhecer melhor os tipos de correntes, as suas aplicações e o dimensionamento das correntes de rolos.
REFLITA
Uma fábrica tem vários equipamentos, entre os quais uma máquina que estava em manutenção, pois apresentava correntes de roletes que estavam chicoteando. Quais as possíveis causas desse problema? Após uma avaliação minuciosa, os operadores chegaram à conclusão de que as razões foram as seguintes: folga excessiva, carga pulsante, articulações endurecidas e desgaste desigual. E se a correia estivesse com ruído, quais seriam as causas? Pare e pense um pouco!
Fonte: Adaptado de Amaral (2000).
Principais tipos de correntes e aplicações
As correntes transmitem força e potência, que fazem com que o eixo gire no sentido horário ou no sentido anti-horário. Quanto à posição, os eixos devem estar, preferencialmente, na horizontal e paralelos entre si, e as rodas dentadas no mesmo plano (NIEMANN, 1971b).
Fonte: Hebert Santos / Pexels.
Além da corrente de rolos, existem outros tipos. Na Figura 1.11, podemos analisar alguns dos tipos existentes no mercado. As correntes de rolo padrão e de rolo padrão com duas faixas são utilizadas na transmissão de potência (objetivo de nosso estudo). Já as correntes de transmissão de passo duplo e a transportadora de passo duplo são utilizadas com a função de transporte de cargas.

Fonte: Mott (2015, p. 296).
#PraCegoVer : a figura mostra cinco tipos de correia, identificados com as letras de a) a e) na sequência, de cima para baixo, sendo: a) corrente de rolo padrão, faixa única; b) corrente de rolo padrão, duas faixas (também disponível com três ou quatro faixas); c) corrente de rolo da série pesada; d) corrente de transmissão de passo duplo; e e) corrente transportadora de passo duplo.
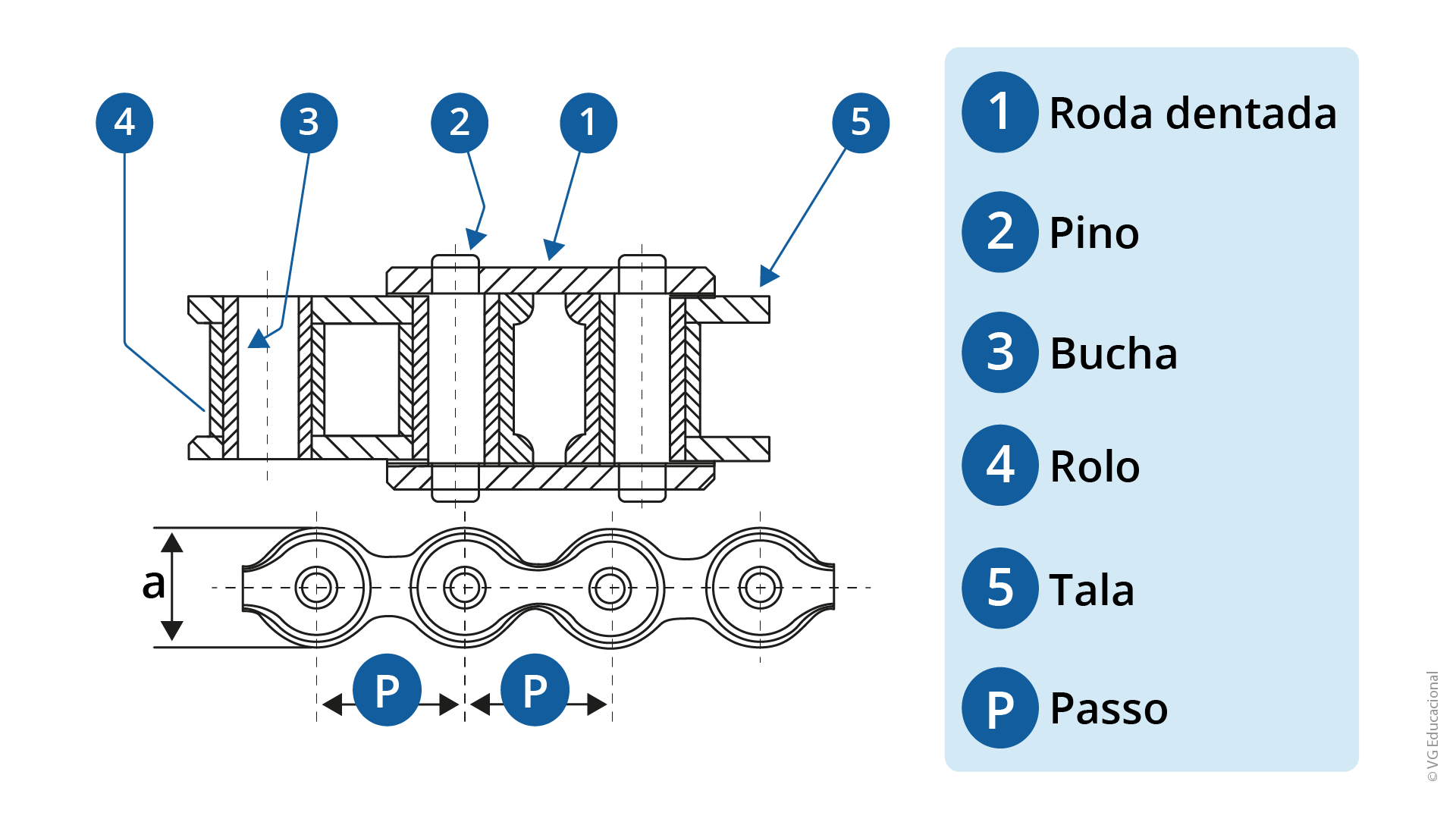
A corrente de rolo é classificada pelo seu passo (distância entre os centros dos rolos). A Figura 1.12 mostra as partes principais de uma corrente de rolos, que são: pino, bucha, rolo e tala.
As engrenagens de correntes ou rodas dentadas também apresentam alguns parâmetros importantes no dimensionamento do conjunto de transmissão, como podemos ver na Figura 1.13:
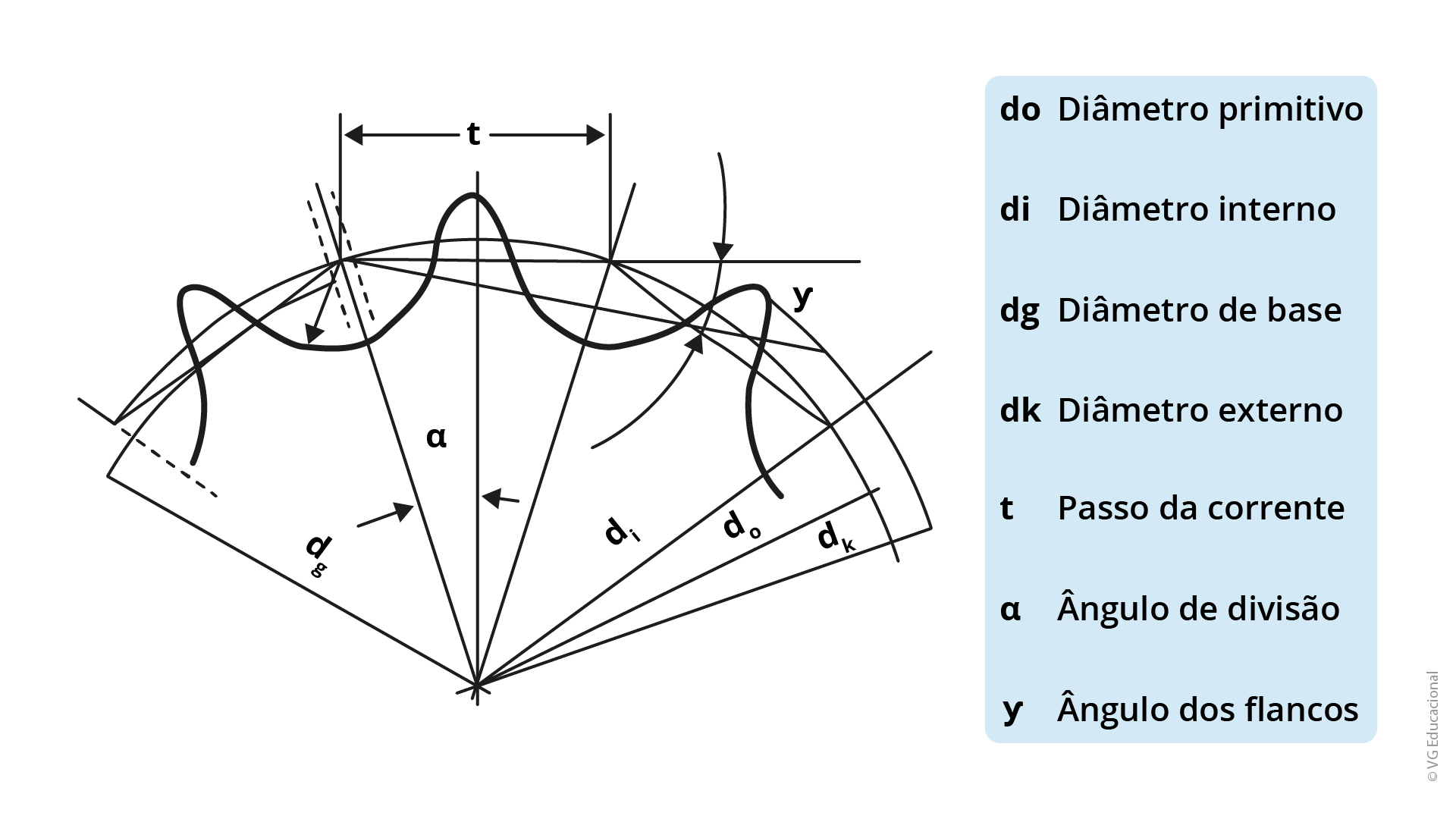
Fonte: Adaptada de Melconian (2019).
#PraCegoVer : a figura mostra os parâmetros da roda dentada, sendo: do – diâmetro primitivo; di – diâmetro interno; dg – diâmetro de base; dk – diâmetro externo; t – passo da corrente; 𝛼 – ângulo de divisão e 𝛾 – ângulo dos flancos.
No próximo subtópico, vamos ver o dimensionamento das correntes de rolos.
Dimensionamento e seleção de correntes e engrenagens
Como já mencionado, as correntes que transmitem potência trabalham em conjunto com as rodas dentadas, e a posição ideal de trabalho é a horizontal. Devido ao peso próprio da corrente, a parte inferior trabalha com certa folga, enquanto a parte superior da corrente trabalha com aperto, como pode ser visto na Figura 1.14.
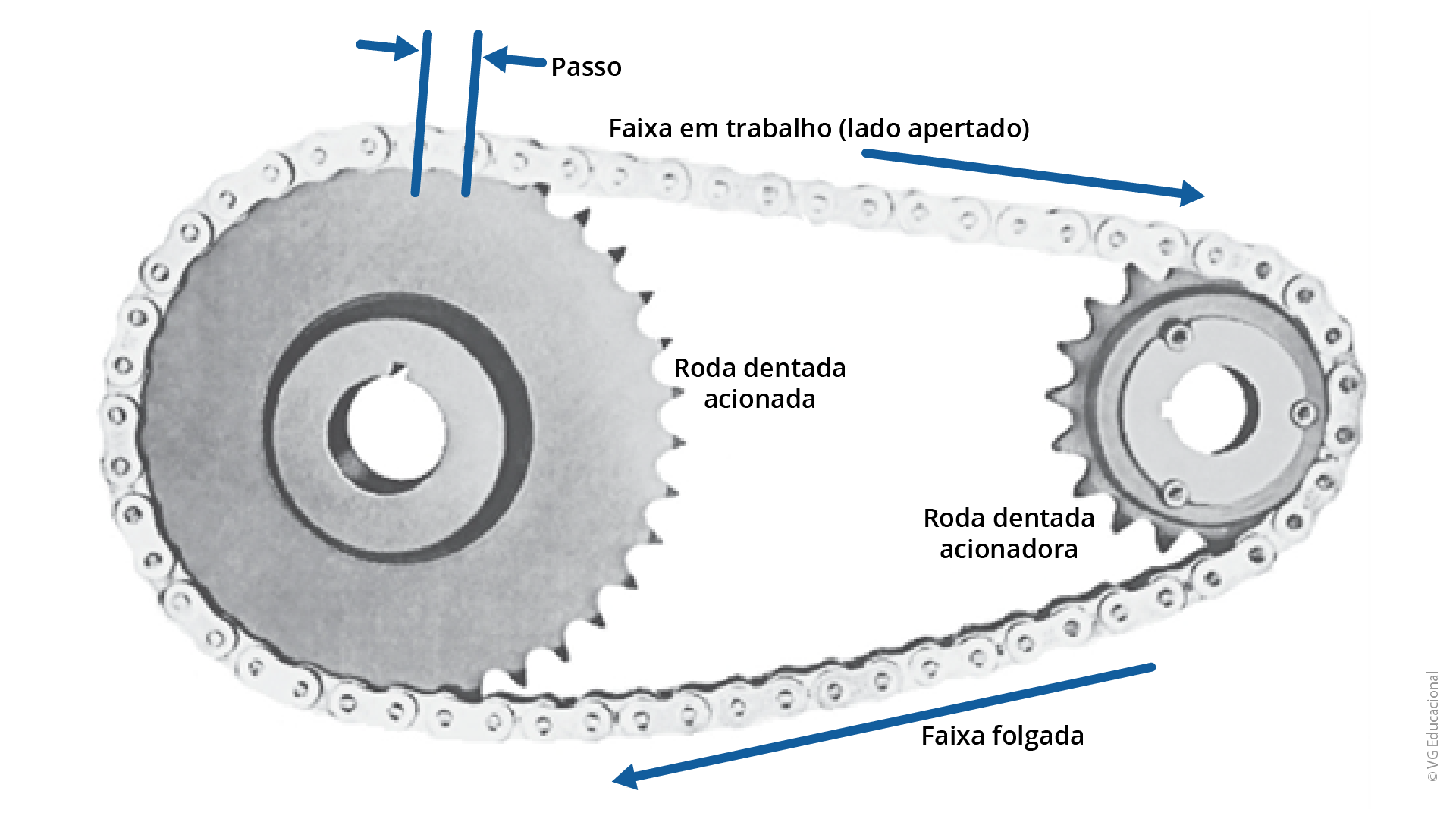
Fonte: Mott (2015, p. 296).
#PraCegoVer : desenho de uma transmissão por corrente, com fundo branco. Do lado mais à esquerda, está a roda dentada acionada de tamanho maior, e à direita está a roda dentada acionadora de tamanho menor. A figura mostra que a parte superior da transmissão trabalha apertada, enquanto a parte inferior da transmissão trabalha folgada.
A seleção do conjunto corrente e roda dentada exige uma sequência de cálculos, e algumas premissas devem ser consideradas até antes de começar o cálculo propriamente dito. Muitos dados utilizados nos cálculos são retirados de tabelas normalizadas e de tabelas de fabricantes.
Saiba Mais
O artigo apresenta o dimensionamento de uma transmissão por corrente de um veículo off-road tipo BAJA SAE. No artigo, foram consideradas duas etapas de redução, e a relação de redução foi calculada, chegando-se a uma relação de redução de 9,5:1. Para ler o artigo, acesse o link a seguir.
https://www.confea.org.br/sites/default/files/antigos/contecc2017/mecanica/10_ddsdtducbsb.pdf
Prezado(a) estudante, antes de começarmos o cálculo, algumas diretrizes precisam ser definidas, conforme listado no Quadro 1.5. Tais diretrizes dizem respeito ao número de dentes das rodas dentadas, que devem ser ímpares, preferencialmente, sendo que o pinhão deve ter, no mínimo, 17 dentes e, no máximo, 120. Quanto à distância entre centros das rodas dentadas, esta deve estar entre 30 e 50 vezes o passo da corrente. A velocidade periférica das correntes de rolos não deve ultrapassar o valor de 12 m/s, devido ao alto ruído causado pelas altas velocidades. A disposição ideal para a transmissão por corrente é na posição horizontal, por conta do peso da corrente, mas o trabalho em outras posições também é possível. Vamos ao quadro para entendermos isso melhor?
Fonte: Mott (2015).
#PraCegoVer : quadro com duas colunas e com oito linhas contendo seis diretrizes. Na primeira linha, está o título do quadro: “Diretrizes para o projeto de correntes de rolos”. Na linha 2, vem a primeira diretriz: “1. Número mínimo de dentes da roda = 17”; na linha 3: “2. Índice de velocidade máximo = 7,0”; na linha 4: “3. Distância entre centros = (30 a 50).passo”; na linha 5: “4. Número máximo de dentes da roda = 120”; na linha 6: “5. Disposição ideal: horizontal e aperto em cima”; na linha 7: “6. Velocidade periférica máxima = 12 m/s”; e na linha 8: “7. O número de dentes da roda dentada deve ser, preferencialmente, um número ímpar”.
O dimensionamento da corrente vai desde a seleção da relação de transmissão até chegarmos ao número de elos da corrente e o comprimento desta. Vamos apresentar as equações e as tabelas no passo a passo do método de dimensionamento. Existem alguns métodos diferentes para o cálculo das correntes.
O método aqui abordado é o da Norma GOST-URSS, apresentado em Melconian (2019).
1º passo : relação de transmissão (i).
Com as rotações dos equipamentos envolvidos (motor e movido), calculamos a relação de transmissão pela seguinte relação:
\[i=\frac{N_{maior}}{N_{menor}}~(Equação~22)\]
2º passo : número de dentes do pinhão (\(Z_1\)).
Com o valor da relação de transmissão encontrado no passo 1, consultamos o Quadro 1.6 e selecionamos o número de dentes do pinhão. Exemplo: se i = 4, então Z1 = 23 (marcado de vermelho no quadro).
Fonte: Adaptado de Melconian (2019).
#PraCegoVer : quadro com três linhas e sete colunas. A primeira coluna apresenta o tipo de corrente, especificada na terceira linha como “corrente de rolos”. As colunas 2 a 7 apresentam as relações de transmissão com os respectivos números de dentes do pinhão correspondente a corrente de rolos: (1 e 31), (2 e 27), (3 e 25), (4 e 23), (5 e 21) e (6 e 17), sendo o primeiro número a relação de transmissão, e o segundo, o número de dentes do pinhão.
3º passo : definir o passo (t) da corrente.
Quanto menor for o passo da corrente, melhor a transmissão. Para encontrar o passo, deve ser utilizada a tabela 14.4 do Melconian (2019), na qual são usados o número de dentes do pinhão e a rotação dele para selecionar o passo. A rotação que constar na tabela pode ser maior que a rotação do problema, mas nunca menor.
SAIBA MAIS
O vídeo “Kit relação: como escolher marca, corrente com retentor ou sem, tipo de aço da coroa e do pinhão” explica as diferenças importantes de qualidade e durabilidade entre corrente, coroa e pinhão, que podem ser comprados no mercado de reposição. Você vai descobrir como verificar se os componentes são certificados pelo Inmetro, o que muda nos tipos de aço 1023 e 1045 e nas correntes com e sem retentor o'ring.
4º passo : velocidade periférica da corrente (vp).
A velocidade periférica não deve ultrapassar o valor de 12 m/s e deve ser calculada da seguinte forma:
\[V_P=\frac{Z_1.t.N_1}{60.1000}~(Equação~23)\]
Em que:
\(V_p\) = velocidade periférica [m/s];
\(Z_1\) = número de dentes do pinhão;
t = passo da corrente [mm];
\(N_1\) = rotação do pinhão [rpm].
Caso a velocidade ultrapasse o valor de 12 m/s, deve-se reduzir o passo e recalcular a corrente.
5º passo : fator de operação (K).
O fator de operação (K) é dado por:
\[K = K_s.K_l.K_{po}~(Equação~24)\]
Em que:
\(K_s\) = fator de serviço;
\(K_l\) = fator de lubrificação;
\(K_{po}\) = fator de posição.
Os valores dos fatores estão no Quadro 1.7, a seguir.
Fonte: Elaborado pela autora.
#PraCegoVer : quadro com os fatores de operação. Na primeira e na segunda coluna, estão os fatores de serviço (Ks), com suas respectivas situações, sendo: 1,0 – carga constante, op. intermitente; 1,3 – com impactos, op. contínua; e 1,5 – fortes impactos, op. contínua. Nas colunas 3 e 4, estão os fatores de lubrificação (Kl), sendo: 1,0 – lubrificação contínua; e 1,3 – lubrificação periódica. Nas colunas 5 e 6, estão os fatores de posição (Kpo), sendo: 1,0 – horizontal ou inclinação < 45°; e 1,3 – Inclinação > 45°.
6º passo : força tangencial na corrente (FT).
A força tangencial é dada pela razão entre a potência e a velocidade periférica, sendo calculada por:
\[F_(T )=\frac{P}{v_p}~(Equação~25)\]
Em que:
\(F_T\) = força tangencial [N];
P = potência [W];
\(V_p\) = velocidade periférica da corrente [m/s].
7º passo : carga de ruptura da corrente (Frup).
Em que a força de ruptura é dada pela força tangencial (\(F_T\)) multiplicada por um coeficiente de segurança (\(n_s\)), encontrado na Tabela 14.3 do Melconian (2019), e pelo fator de operação (K), calculado no 5º passo:
\[Frup = F _T.n_s.K~(Equação~26)\]
8º passo : verificação da distância entre centros (C).
A distância entre centros deve estar entre 30 a 50 vezes o valor do passo. Com o passo encontrado, deve-se verificar a distância entre centros por:
\[30 < \frac{C}{t}< 50~(Equação~27)\]
9º passo : cálculo do número de elos da corrente (y).
O número de elos da corrente é calculado levando em consideração o número de dentes das rodas dentadas (\(Z_1\) e \(Z_2\)), a distância entre centros (C, em mm) e o passo das correias (t, em mm). Esses parâmetros estão relacionados da seguinte forma:
\[y = \frac{Z_1+Z_2}{2}+\frac{2C}{t}+\left ( \frac{Z_2-Z_1}{2\pi } \right )^2 \cdot \frac{t}{C}~(Equação~28)\]
10º passo : comprimento da corrente (l).
Como último passo, calcula-se o comprimento da corrente, multiplicando o número de elos pelo passo, sendo:
\[l =y.t~(Equação~29)\]
Numa transmissão por corrente, foi dimensionado um pinhão com 25 dentes e uma coroa com 75 dentes. A distância entre eles é de 500 mm, e o passo da correia foi definido em ½" (meia polegada). Conversão de unidades: 1 pol = 25,4 mm.
Nessas condições, o número de elos da corrente e o comprimento da corrente, respectivamente, são iguais a:
Prezado(a) estudante, você já viu aqueles grandes guindastes erguendo cargas bem pesadas? Já andou de elevador? Essas são algumas das aplicações dos cabos de aço, que são utilizados para o transporte e a elevação de cargas.
Neste tópico, vamos falar um pouco sobre os cabos de aço, suas aplicações e o procedimento de seleção.
Principais tipos de cabos de aço e aplicações
Os cabos de aço são compostos por um núcleo e arames enrolados em torno desse núcleo. O núcleo, também chamado de alma, pode ser de fibra (natural ou artificial) ou, quando sujeito a calor, de aço (SHIGLEY, 1984). Os arames em torno da alma são enrolados de diferentes formas (enrolamento diagonal ou lang, à direita ou à esquerda). Para entendermos melhor esse conceito, vamos analisar a Figura 1.15, a seguir, que mostra as possibilidades de enrolamento dos arames.
Os cabos de aço também podem ser classificados pelo material da alma, que pode ser de aço (AA), de fibra natural (AF) ou de fibra artificial (AFA). As fibras naturais mais utilizadas são o sisal e o rami, e a artificial mais utilizada é o polipropileno. As desvantagens das fibras artificiais se relacionam ao fato de serem mais caras e, por isso, utilizadas em cabos especiais. As almas de aço podem ser formadas por uma perna de cabo (AA) ou por um cabo de aço independente (AACI). Este último oferece mais flexibilidade e maior resistência à tração (SHIGLEY, 1984).
Os cabos de aço são muito aplicados em elevação de grandes cargas, como em elevadores e guindastes. Podem transmitir movimento através de grandes distâncias e com grande potência, sem necessidade de as polias estarem perfeitamente alinhadas, já que elas possuem ranhuras (SHIGLEY, 1984).
Elementos de transmissão
Quais os elementos de transmissão flexíveis e quais as suas principais características?
#PraCegoVer : o infográfico, em forma de figura de fundo, apresenta três abas para interagir sobre ela. O infográfico tem como título geral “Elementos de transmissão” e, em seguida, há uma pergunta: “Quais os elementos de transmissão flexíveis e quais as suas principais características?”. Logo após, há as três abas com três possíveis respostas para a pergunta apresentada, sendo elas: 1ª aba “Correias: as correias são elementos de transmissão flexíveis, utilizadas em grandes distâncias de eixos. Possuem baixo ruído e são as mais econômicas, principalmente quando comparadas com as correntes e com as engrenagens”; 2ª aba “Correntes: correntes são elementos de transmissão flexíveis que têm como vantagem não apresentar deslizamentos nem estiramentos. Além disso, possuem longa duração e flexibilidade no acionamento de vários eixos, a partir de uma única fonte motora”; 3ª aba “Cabos de aço: os cabos de aço são amplamente utilizados em levantamento de altas cargas, como nos guindastes, elevadores etc.”. A figura de fundo se trata de metade do tronco de uma pessoa vista de frente, que utiliza luva de segurança em suas mãos e segura um capacete de trabalho de obras. A imagem tem tom esverdeado, com foco somente no capacete, que se destaca pela cor amarela. É possível identificar um prédio em construção ao fundo da pessoa na figura, que está desfocada.
Quanto ao material, os cabos de aço podem ser de aço galvanizado, aço inoxidável, aço polido e aço revestido. Os cabos de aço inoxidável são utilizados na indústria química, devido à sua alta resistência à corrosão. Os de aço galvanizado, por serem também resistentes à corrosão, são muito usados na indústria naval. Já os cabos de aço polido são utilizados quando a corrosão não é uma grande preocupação (na indústria civil, por exemplo). Já os cabos de aço revestido são feitos de aço polido com um revestimento de PVC e são utilizados na indústria marítima (SALES, 2019).
Na próxima subseção, vamos falar um pouco sobre como os cabos de aço são selecionados para suas aplicações.
Seleção e informações adicionais
De acordo com a ISO 17893, os cabos de aço são designados pelo diâmetro do cabo, pelo número de pernas e pelo número de fios. Por exemplo: a indicação “cabo de 1.½" pol. 6 x 7” significa que o cabo tem 1.1⁄2" polegadas de diâmetro e tem 6 pernas com 7 fios de arame em cada perna. Na identificação dos cabos, podem vir letras que estão relacionadas ao tipo da alma, como AA, AACI, AF ou AFA (SHIGLEY, 1984).
SAIBA MAIS
O vídeo a seguir mostra algumas aplicações dos cabos de aço como em elevadores, escavadeiras e pontes rolantes. O vídeo também mostra a estrutura dos cabos em alma e pernas e explica essa estrutura de forma visual, bem como a construção dos cabos.
Alguns fatores devem ser levados em conta na seleção de cabos de aço. São eles: a) resistência à tração, devido à solicitação de levantamento de carga; b) deformação elástica, para evitar grandes alongamentos; c) durabilidade, para que haja mais segurança na transmissão.

Projeto de máquinas: uma abordagem integrada
Editora : Bookman
Autor : Robert. L. Norton
ISBN : 978-85-8260-023-8
Comentário : O livro apresenta diversos estudos de casos reais, o que possibilita ao estudante ter acesso a diversas situações que podem ser encontradas em sua futura profissão. O livro também utiliza métodos computadorizados para a solução de problemas, o que faz o estudante se familiarizar com esse tipo de abordagem.
Telecurso 2000 - Elementos de Máquinas - 26 Introdução aos elementos de transmissão
Ano : 2011
Comentário : O vídeo mostra alguns elementos de transmissão, como as correias, além de tratar sobre os variadores de velocidade por engrenagens, por correias e por atrito e sobre as roscas que transformam o movimento giratório em retilíneo, e vice-versa. O vídeo permite ao estudante ter contato visual com alguns dos elementos que estão sendo estudados no nosso curso.
Prezado(a) estudante, chegamos ao final do nosso estudo, e, como você pôde ver, os elementos de transmissão , dos tipos elásticos, correias, correntes e cabos de aço, têm ampla aplicação em equipamentos diversos.
Você viu também que, para dimensionar e calcular esses elementos, é preciso bom conhecimento de mecânica , além de ser necessário consultar diversas tabelas e equações. Todavia, apesar da grande quantidade de cálculos, vimos que, seguindo um passo a passo bem definido, até que fica fácil, não é mesmo?
Bons estudos, e até breve!
BUDYNAS, R. G.; NISBETT, J. K. Elementos de máquinas de Shigley . 10. ed. Porto Alegre: AMGH, 2016.
CÁLCULO correia de transmissão. [ S. l.: s. n .], 2016. 1 vídeo (28 min 47 s). Publicado pelo canal Manual do Engenheiro. Disponível em: https://www.youtube.com/watch?v=sNWkJawDGEA . Acesso em: 13 maio 2021.
EIXOS e correntes. [2021]. Disponível em: https://essel.com.br/cursos/material/01/Manutencao/22manu2.pdf . Acesso em: 16 abr. 2021.
FRANCESCHI, A. de; ANTONELLO, M. G. Elementos de máquinas . Santa Maria, RS: Rede e-Tec Brasil, 2014.
KIT relação: como escolher marca, corrente com retentor ou sem, tipo de aço da coroa e do pinhão. [ S. l.: s. n. ], 2019. 1 vídeo. (2 min 34 s). Publicado pelo canal Duas Rodas. Disponível em: https://www.youtube.com/watch?v=MkdhKWvo9j8 . Acesso em: 13 maio 2021.
MELCONIAN, S. Elementos de máquinas . 11. ed. São Paulo: Érica, 2019.
MOTT, R. L. Elementos de máquinas em projetos mecânicos . 5. ed. São Paulo: Pearson Education do Brasil, 2015.
NIEMANN, G. Elementos de máquinas : volume 1. São Paulo: Blucher, 1971a.
NIEMANN, G. Elementos de máquinas : volume 3. São Paulo: Blucher, 1971b.
NORTON, R. L. Projeto de máquinas : uma abordagem integrada. 4. ed. Porto Alegre: Bookman, 2013.
SALES, R. 4 tipos de cabo de aço usados na indústria. Acoplast Brasil , 2019. Disponível em: https://blog.acoplastbrasil.com.br/tipos-de-cabo-de-aco/ . Acesso em: 28 abr. 2021.
SHIGLEY, J. E. Elementos de máquinas . Rio de Janeiro: LTC, 1984.
SILVA, M. W. S. da et al . Dimensionamento do sistema de transmissão por corrente de um carro BAJA SAE. In : CONGRESSO TÉCNICO CIENTÍFICO DA ENGENHARIA E DA AGRONOMIA, Semana Oficial da Engenharia e da Agronomia, 74., 2017, Belém, PA. Anais eletrônicos [...]. Belém, PA: Confea, 2017. Disponível em: https://www.confea.org.br/sites/default/files/antigos/contecc2017/mecanica/10_ddsdtducbsb.pdf . Acesso em: 23 abr. 2021.
TECNOLOGIA Japonesa de Mola de Ultraprecisão. [ S. l.: s. n. ], 2018. 1 vídeo (4 min 38 s). Publicado pelo canal Japan Video Topics – Português. Disponível em: https://www.youtube.com/watch?v=1zL9hAQdDGE . Acesso em: 28 abr. 2021.
TELECURSO 2000 – Elementos de Máquinas – 26 Introdução aos elementos de transmissão. [ S. l.: s. n. ], 2011a. 1 vídeo (12 min 54 s). Publicado pelo canal Bruno Albert. Disponível em: https://www.youtube.com/watch?v=NL-Ldch3GQw . Acesso em: 13 maio 2021.
TELECURSO 2000 – Elementos de Máquinas – 30 Cabos. [ S. l.: s. n. ], 2011b. 1 vídeo (13 min 23 s). Publicado pelo canal Bruno Albert. Disponível em: https://www.youtube.com/watch?v=Fbyd9CYHQaI . Acesso em: 23 abr. 2021.