Estatística e Probabilidade Aplicada
Distribuições de Probabilidade Discreta
Estatística e Probabilidade Aplicada
Distribuições de Probabilidade Discreta
Nesta unidade, utilizaremos os resultados da estatística descritiva, apoiados com a teoria básica das probabilidades para estudar algumas distribuições de probabilidade.
As distribuições de probabilidade estão presentes em diversas aplicações do nosso dia a dia, como na realização de experimentos simples (como lançamento de um dado) e em exemplos mais complexos (como implantar um sistema de controle da qualidade em uma linha de produção industrial).
Neste momento, concentraremos nossa atenção para as distribuições discretas, focando nas Distribuições Binomial e de Poisson. Em outra oportunidade, trabalharemos com a distribuição contínua mais estudada no mundo: a distribuição Normal.
Bons estudos!
Variáveis aleatórias são variáveis que assumem valores numéricos para cada resultado de um experimento. Ainda, para ser classificada como aleatória, a variável deve ser associada a valores determinados pelo acaso.
Para ilustrar o conceito de variável aleatória, considere o lançamento simultâneo de dois dados. A tabela seguinte representa a combinação de possibilidades de resultados do experimento.
Uma possível variável aleatória para esse experimento seria contar quantas vezes sai o número 5 nesse lançamento:
Variável aleatória:
X : número de vezes que sai o número 5 no lançamento de dois dados.
Observe que existem 3 possibilidades de valores para a variável aleatória X:
\({{x}_{1}}=0\) , \({{x}_{2}}=1\) e \({{x}_{3}}=2\).
Para cada variável aleatória, podemos relacionar uma distribuição de probabilidade , que consiste em uma associação na qual, para cada valor \(\left( {{x}_{i}} \right)\) da V.A., associamos a sua probabilidade de ocorrência \(\left( P({{x}_{1}} \right)={{p}_{i}})\).
No exemplo do lançamento dos dados, para o caso da variável aleatória que definimos, a distribuição de probabilidade é dada por:
Toda variável aleatória que possui uma quantidade enumerável de valores possíveis \(\left( {{x}_{i}} \right)\) é classificada como discreta. Por exemplo, no caso da variável aleatória de contagem do resultado 5 no lançamento do dado, temos um conjunto de três possibilidades (0, 1 e 2). Logo, esse é um exemplo de variável aleatória discreta.
Considere, agora, a quantidade de litros de óleo diesel produzidos em uma indústria. Observe que as possibilidades de resultados para essa V.A. não se restringem a números inteiros (0 litros, 1 litro, 2 litros, 3 litros,..., n litros,...), podendo assumir qualquer valor real positivo, por exemplo, 3,816 litros. Nesse caso, estamos tratando de uma variável aleatória contínua .
Como já mencionado, esta unidade será destinada para as variáveis discretas. Em outra oportunidade, você conhecerá mais sobre as variáveis contínuas.
Um histograma é um gráfico de barras que associa cada classe a uma frequência, podendo ser uma frequência absoluta ou relativa.
Para o caso das distribuições de probabilidade, o histograma terá cada classe representando os possíveis resultados da variável aleatória. O eixo vertical indicará a probabilidade de ocorrência de cada classe.
O histograma a seguir representa a distribuição de probabilidade da variável aleatória X já mencionada anteriormente (número de vezes que sai o número 5 no lançamento de dois dados).
Como estamos trabalhando com probabilidades, duas características comuns a todas as distribuições podem ser observadas no histograma anterior:
De modo análogo à forma que as medidas de média, variância e desvio-padrão, podemos associar tais valores a cada variável aleatória. Ou seja, para cada experimento, podemos definir várias variáveis aleatórias que, por sua vez, para cada V.A. será associada a uma distribuição de probabilidades que, assim terá uma média, uma variância e um desvio-padrão.
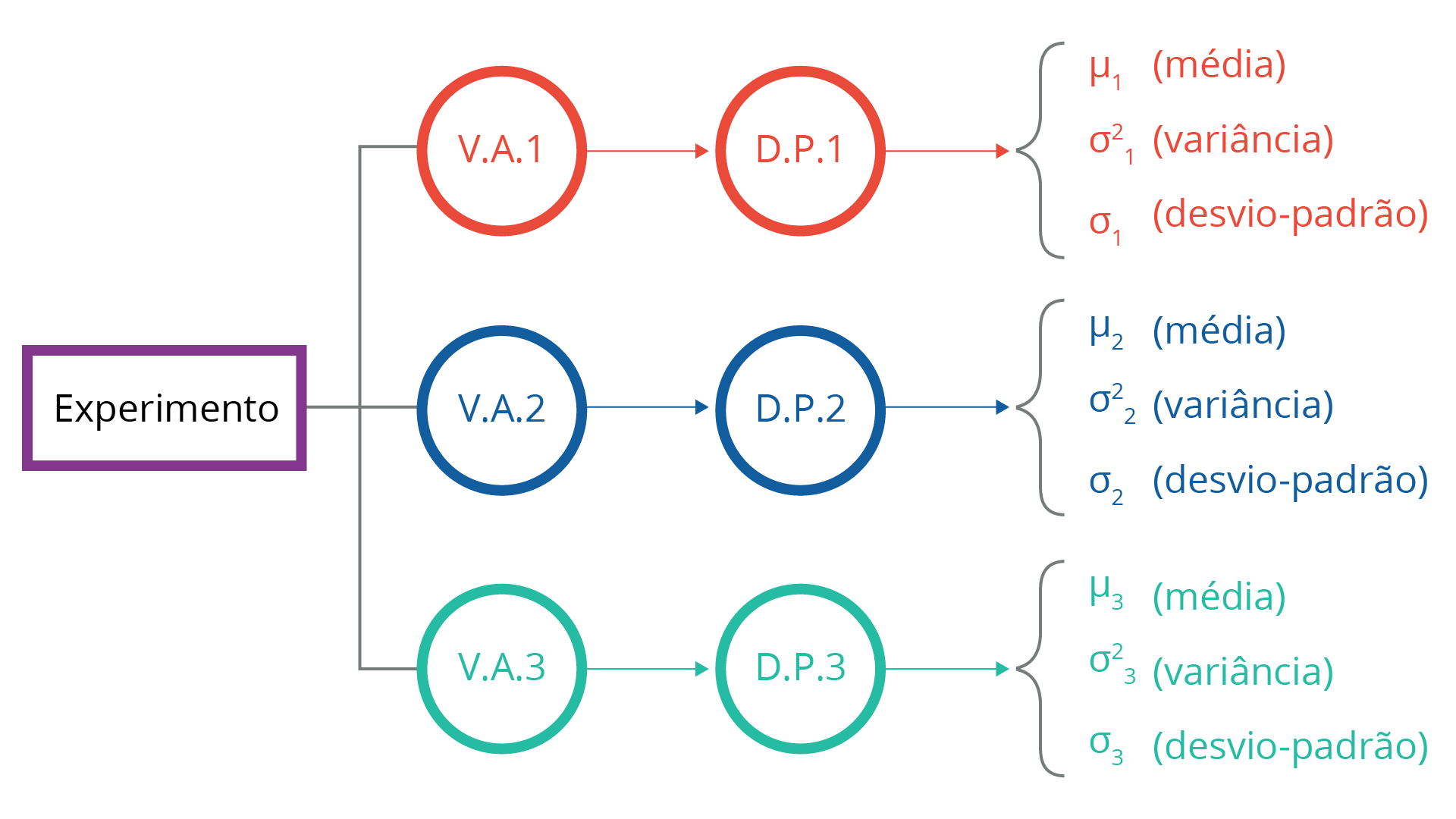
A tabela seguinte contém a relação de fórmulas utilizadas para o cálculo dessas medidas de tendência central e dispersão.
No exemplo da variável aleatória X (número de vezes que sai o número 5 no lançamento de dois dados), teremos as seguintes medidas.
1. MÉDIA
\(\mu =0\cdot \frac{25}{36}+1\cdot \frac{10}{36}+2\cdot \frac{1}{36}=\frac{12}{36}\simeq 0,33\) vezes
2. VARIÂNCIA
\({{\sigma }^{2}}={{\left( 0-0,33 \right)}^{2}}\cdot \frac{25}{36}+{{\left( 1-0,33 \right)}^{2}}\cdot \frac{10}{36}+{{\left( 2-0,33 \right)}^{2}}\cdot \frac{1}{36}\simeq 0,28\) vezes ao quadrado
3. DESVIO-PADRÃO
\(\sigma =\sqrt{0,28}\simeq 0,53\) vezes
A média, em uma V.A. discreta também é chamada de valor esperado da variável.
A tabela a seguir corresponde à variável aleatória X que corresponde ao número de banheiros em uma residência brasileira em dezembro de 2019.
A partir dos dados da tabela, assinale a alternativa que corresponde ao número médio de banheiros no Brasil em dezembro de 2019.
Agora que você já conhece as características gerais de uma variável aleatória discreta e sua distribuição de probabilidade, vamos nos concentrar no estudo de uma V.A. específica que gera uma distribuição de probabilidade muito utilizada em problemas do dia a dia de qualquer profissional da área de exatas: a distribuição Binomial.
Uma distribuição de probabilidade binomial resulta de um experimento que satisfaz os seguintes requisitos:
1. O experimento tem um número finito de tentativas.
2. As tentativas devem ser independentes (o resultado de qualquer tentativa individual não afeta as probabilidades nas outras tentativas).
3. Cada tentativa deve ter todos os resultados classificados em duas categorias (em geral, chamadas de sucesso e fracasso).
4. A probabilidade de sucesso permanece constante em todas as tentativas (TRIOLA, 2013, p. 180).
Para exemplificar, voltemos ao exemplo da distribuição \(X\) já trabalhada na seção anterior (número de vezes que sai o número 5 no lançamento de dois dados). Observe que nesse caso temos satisfeitos os quatro requisitos da definição de probabilidade binomial:
Em qualquer distribuição binomial, a probabilidade de ocorrência de sucessos em um conjunto de tentativas pode ser calculada a partir da expressão seguinte:
\[P\left( x \right)=\frac{n!}{\left( n-x \right)!x!}{{p}^{x}}{{q}^{n-x}},~~~~~~~\text{(equação A)}\]
sendo:
Exercício resolvido:
No lançamento de dois dados não viciados, qual é a probabilidade de ocorrência de exatamente UM resultado igual a 5?
Solução:
Nesse exemplo, temos que \(n=2\) (dois lançamentos), \(x=1\) (um sucesso), \(p=1/6\) e \(q=5/6\).
Aplicando a equação A, temos:
\[P\left( 1 \right)=\frac{2!}{\left( 2-1 \right)!1!}\cdot {{\left( \frac{1}{6} \right)}^{1}}\cdot {{\left( \frac{5}{6} \right)}^{2-1}}=\frac{2}{1\cdot 1}\cdot \frac{1}{6}\cdot \frac{5}{6}=\frac{10}{36}\]
Observe que o resultado encontrado no exercício acima coincide com o valor indicado na distribuição de probabilidade da V.A. X, calculada na seção 1.
A distribuição binomial é assim denominada em virtude dos seus cálculos de probabilidade serem semelhantes ao desenvolvimento do binômio \(B={{\left( x+y \right)}^{a}}\).
Para fixação do conteúdo, vamos a mais um exemplo do uso da fórmula A.
Exemplo:
A marca BRverde é uma empresa especializada em comunicação voltada para a conscientização da população brasileira sobre os cuidados que devemos ter com o meio ambiente e as consequências que podem resultar de um consumismo desenfreado.
Para verificar a eficácia de suas ações, a empresa realizou uma enquete e constatou que apenas 17% da população de Recife reconhecem a sua marca.
Numa família de 35 pessoas residentes em Recife, qual é a probabilidade de 2 ou menos pessoas conhecerem a marca BRverde?
Solução:
Para responder a essa pergunta, considere o experimento que consiste em escolher um dos 35 familiares e verificar se ele conhece (sucesso) ou não (fracasso) a marca BRverde. O que se deseja descobrir, para a população n=35, é a probabilidade para \(x\le 2\).
Observe que a probabilidade de sucesso é igual a 17/100~=~0,17. Sendo assim, a probabilidade de fracasso é igual a 1-0,17=0,83.
Aplicando a fórmula:
\[P(0)= \frac{35!}{(35-0)!0!} \cdot (0,17)^0\cdot (0,83)^{35-0}=1,47\cdot 10^{-3}\]
\[P(1)= \frac{35!}{(35-1)!1!}\cdot(0,17)^1\cdot(0,83)^{35-1}=1,05\cdot10^{-2}\]
\[P(2)= \frac{35!}{(35-2)!2!}\cdot(0,17)^2\cdot(0,83)^{35-2}=3,67\cdot10^{-2}\]
Como \(P_{(x\leq 2)} = P (0)+P(1)+P(2)\), temos:
\[P_{(x\leq 2)} = 0,00147+0,01054+0,03672 = 0,04873 = 4,87\text{%}\].
Uma prova contém 10 questões de múltipla escolha com 5 alternativas. Para acertar uma questão, o aluno precisa assinalar a única alternativa que é correta. Nesse contexto, assinale a alternativa que apresenta a probabilidade de um aluno que “chuta” todas as questões acertar exatamente 3 exercícios?
Agora que já sabemos identificar distribuições binomiais e calcular as probabilidades nesse contexto, vamos aprender a determinar as principais medidas de tendência central e dispersão.
A tabela a seguir corresponde às fórmulas para os cálculos de média, variância e desvio-padrão (restritos apenas às distribuições binomiais).
Para exercitar, vamos calcular (mais uma vez) a média, a variância e o desvio-padrão para a variável aleatória X que corresponde ao número de vezes que sai o número 5 no lançamento de dois dados.
1. MÉDIA:
\(mu =np=2\cdot \frac{1}{6}\simeq 0,33\) vezes
2. VARIÂNCIA
\({{\sigma }^{2}}=npq=2\cdot \frac{1}{6}\cdot \frac{5}{6}\simeq 0,28\) vezes ao quadrado
3. DESVIO-PADRÃO
\(\sigma =\sqrt{0,28}\simeq 0,53\) vezes
Observe que os resultados encontrados coincidem com os obtidos quando aplicadas as fórmulas para distribuições discretas gerais.
Definimos que, em um dado experimento, um valor é classificado como não usual quando este se distancia da média em um valor superior ao dobro do desvio padrão.
Considerando que uma pesquisa foi feita com 894 clientes de uma empresa, constatou-se que 193 votaram na opção A, conforme figura seguinte:
Pensando em um resultado estimado para essa pesquisa, determine o valor mínimo usual de votos na opção A e assinale a alternativa correspondente.
Para finalizar nosso estudo sobre variáveis discretas, concentraremos nossa atenção a mais uma clássica distribuição: a distribuição de Poisson.
A distribuição de Poisson é uma distribuição de probabilidade discreta que se aplica a ocorrências de eventos ao longo de intervalos especificados. A variável aleatória \(x\) é o número de ocorrências do evento no intervalo. O intervalo pode ser de tempo, distância, área, volume ou alguma unidade simular. A probabilidade de ocorrência de \(x\) vezes em um intervalo é dada pela fórmula:
\[P\left( x \right)=\frac{{{\mu }^{x}}\cdot {{e}^{-\mu }}}{x!}\]
em que \(e\simeq 2,7182.\)
(TRIOLA, 2013, p. 193)
Para que a fórmula anterior possa ser aplicada, devemos ter certeza de estar trabalhando com um evento situado em algum intervalo, além de garantir que cada ocorrência seja aleatória, independente e uniformemente distribuída nesse intervalo.
Para exemplificar, considere o seguinte:
Na construção de um prédio residencial, ocorreram, nos últimos 42 dias, 17 acidentes de trabalho. Selecionando-se ao acaso um determinado dia, dentre os 42 avaliados, qual é a probabilidade de ter ocorrido 3 acidentes nesse dia?
Para responder a essa pergunta, considere uma distribuição de Poisson com média igual a:
\(\mu =\frac{17}{42}=0,4048\) acidentes.
Sendo assim, \(P\left( 3 \right)=\frac{{{0,4048}^{3}}\cdot {{e}^{-0,4048}}}{3!}\simeq 0,007375=0,74%\).
Em um ano bissexto, houve 1687 nascimentos em uma cidade do interior do Rio Grande do Sul. Selecionando aleatoriamente um dia desse ano, assinale a alternativa que apresenta a probabilidade de termos exatamente 2 nascimentos nessa cidade.

Mario F. Triola
Editora: LTC
ISBN: 9788521634256
Comentário: Neste livro, você encontrará outros exemplos e aplicações de todo o conteúdo trabalhado na unidade, além de inúmeros exercícios para fortalecer e fixar seu aprendizado.
Comentário: O vídeo em questão faz parte de uma coleção de materiais didáticos disponíveis gratuitamente no Youtube pela UNIVESP - Universidade Virtual do Estado de São Paulo. Nele você poderá revisar todo o conteúdo da unidade e acessar um canal repleto de materiais sobre estatística e matemática em geral
Para conhecer o vídeo completo, acesse o link a seguir.
O material que você acabou de ler, vai auxiliar em diversos contextos da sua vida profissional, uma vez que qualquer distribuição de probabilidade discreta pode ser estudada sob o viés do conteúdo desta unidade.
Com esse conhecimento, você já está apto a calcular a probabilidade de ocorrência de defeitos em produtos numa linha de produção, calcular a chance de aprovação em uma prova de múltipla escolha, analisar dados estatísticos discretos sobre a ocorrência de um fenômeno e outras diversas aplicações úteis no dia a dia de qualquer pessoa.
Para fixar o conteúdo, não se esqueça de exercitar bastante e, caso ache necessário, revise a unidade.
TRIOLA, Mario F. Introdução à Estatística: atualização da tecnologia. v. único. 11. ed. Rio de Janeiro: LTC, 2013.
UNIVESP. Estatística - Aula 11 - Distribuições de Probabilidade. 2015. Disponível em: https://www.youtube.com/watch?v=j3Zbup0KMxY . Acesso em: 22 dez. 2019.