Estatística e Probabilidade Aplicada
Distribuições de Probabilidade Contínua
Na unidade passada você conheceu a definição de distribuição de probabilidade e pôde trabalhar bastante com as distribuições binomiais e de Poisson. Destinaremos essa unidade ao estudo da distribuição de probabilidade contínua mais trabalhada em todo o mundo: a distribuição Normal (ou distribuição Normal de Gauss).
Com os conhecimentos adquiridos aqui, você se convencerá de como a estatística pode nos auxiliar em decisões corriqueiras do nosso dia a dia, como no dimensionamento da altura de uma porta, ou em situações mais complexas, como avaliar a qualidade da produção de um equipamento numa linha de produção.
Bons estudos!
Considere um conjunto de dados que possui média \(\mu\) e desvio-padrão \(\sigma\). Dizemos que a distribuição de probabilidade é Normal se puder ser descrita pela função:
\[P\left( x \right)=\frac{{{e}^{-\frac{1}{2}{{\left( \frac{x-\mu }{\sigma } \right)}^{2}}}}}{\sigma \sqrt{2\pi }}\]
Fique tranquilo(a)! A função anterior, por conta da sua complexidade, não precisará ser utilizada em nenhum momento ao longo do restante desta unidade. Em substituição, utilizaremos uma tabela com valores previamente calculados e que garantem toda a ferramenta necessária para nosso estudo das distribuições normais.
Uma vez fixados os parâmetros \(\mu\) e \(\sigma\), a função anterior possui como gráfico a curva a seguir.
A curva anterior, por conta do seu formato, é chamada de curva sino , curva normal ou curva de Gauss .
A principal propriedade da curva de Gauss é a sua simetria em torno da média \(\mu\).
OBSERVAÇÃO :
Observe que a lei que define tal curva depende apenas da média e do desvio-padrão. Uma vez alterados esses parâmetros, a curva se altera, mas mantém a forma de sino. A figura a seguir ilustra esse fato.
Iniciaremos nosso estudo assumindo que a média e o desvio-padrão são constantes e iguais a 0 e 1, respectivamente. Nesse caso, chamamos a nossa distribuição normal de padrão . Na próxima seção, aprenderemos a trabalhar com parâmetros diferentes dos assumidos na distribuição-padrão (\(\mu =0\) e \(\sigma =1\)).
Uma distribuição normal padrão tem as propriedades a seguir.
A área sob a curva normal é sempre igual a 1, o que garante a existência de uma correspondência entre tal área e a probabilidade. Dessa fórmula, para calcular alguma probabilidade em uma distribuição normal, calcularemos alguma área abaixo da curva normal.
Como a função que descreve a curva normal é extremamente complexa e o procedimento para determinação de áreas de regiões delimitadas por ela requer densos cálculos, utilizaremos a tabela que consta no fim desta unidade para determinar essas áreas procuradas.
Para usar a tabela, é muito importante que você se atente aos itens a seguir:
Por convenção, utilizaremos a variável \(z\) apenas quando a distribuição for padrão. Para casos gerais, utilizaremos a variável \(x\).
Por exemplo, considere que a variável \(z\) possua distribuição normal com média \(\mu =0\) e desvio-padrão \(\sigma =1\), ou seja, a distribuição é normal padrão. Qual a probabilidade de que \(z\le 1,32\)?
Essa pergunta pode ser respondida com o valor da área indicada em lilás na figura a seguir. Ou seja: a área abaixo da curva de normal para \(z\le 1,32\).
Para determinação dessa área, vamos recorrer à tabela de escores \(z\). Procurando na primeira coluna o valor de 1,3 e na primeira linha o valor de 0,02, obtermos a área (probabilidade) igual a 0,9066. Ou seja: a probabilidade para que \(z\le 1,32\) é igual a 90,66%.
Exercício resolvido 1 :
Utilizando a tabela de escores \(z\), determine a probabilidade para que \(z\ge 0,07\).
Solução :
Observe na figura a seguir a área que corresponde à probabilidade desejada.
Como a tabela de escores \(z\) só nos fornece áreas acumuladas à esquerda de um determinado valor, usaremos a seguinte estratégia: subtrairemos da área total abaixo da curva normal (área total = 1), o valor acumulado à esquerda de 0,61. Ou seja:
\[P\left( z\ge 0,61 \right)=1-P\left( z\le 0,61 \right)\]
Utilizando a tabela de escores z, temos que \(P(z≤0,61)=0,7291\).
Portanto, \(P(z≥0,61)=0,2709\), conforme Figura 4.5.
Num equipamento da indústria têxtil, um dos parâmetros a serem controlados pelos engenheiros de produção é o indicador \(\alpha\). Suponha que esse indicador seja uma medida contínua, normalmente distribuída, com média \(\mu =0\) e desvio-padrão \(\sigma =1\). Calcule a probabilidade para que, num determinado momento, o indicador seja observado entre os números 0,72 e 2,03.
Dica: \(P\left( 0,72\le z\le 2,03 \right)=P\left( z\le 2,03 \right)-P\left( z\le 0,72 \right)\)
Nessa seção, discutiremos como calcular probabilidades para distribuições normais não padronizadas, ou seja, \(\mu \ne 0\) ou \(\sigma \ne 1\).
Nos casos de distribuições não padronizadas, converteremos a variável da questão para escores \(z\), utilizando a relação a seguir.
\[z=\frac{x-\mu }{\sigma }\]
A figura a seguir ilustra a conversão que deve ser realizada. Nela você deve observar que a área procurada permanece a mesma, o que justifica a troca de variáveis.
Exercício resolvido 2:
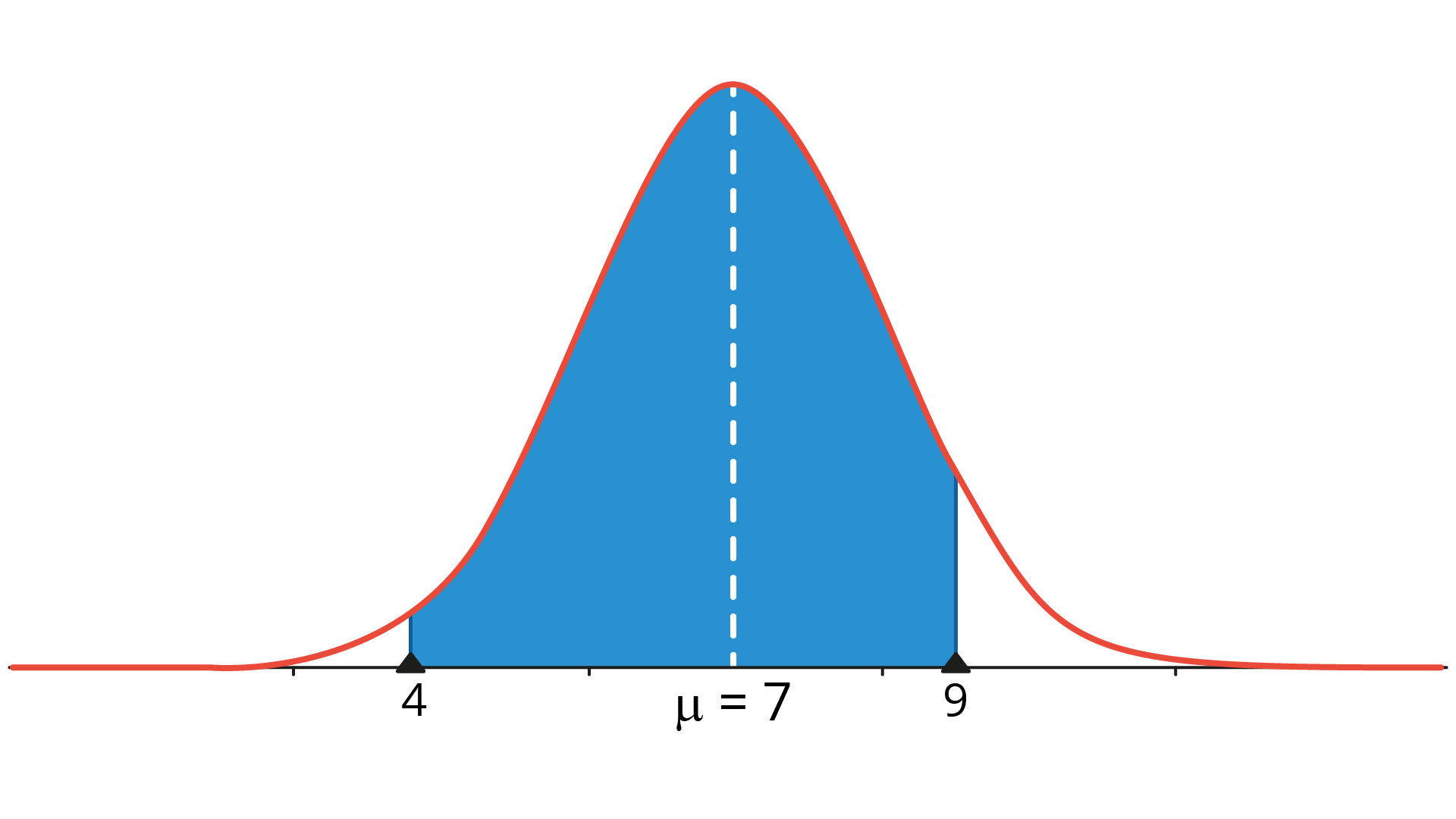
A temperatura de câmaras frigoríficas para armazenamento de vegetais em supermercados é normalmente distribuída, com média de 7ºC e desvio-padrão de 1ºC. Por lei, essas câmaras devem ter temperatura controlada entre 4ºC e 9ºC. Determine o percentual de câmaras frigoríficas que atendem a exigência da legislação.
Solução:
Para responder essa questão, devemos calcular a área indicada em lilás na figura a seguir.
Existem vários critérios (alguns visuais e outros mais quantitativos) para verificação da normalidade de uma população. Por simplificação, assumiremos nessa disciplina que a população está normalmente distribuída quando a curva de densidade apresenta o aspecto de sino. Para uma aplicação mais precisa dos métodos estatísticos apresentados aqui, outros critérios podem ser levados em conta. Esses outros critérios são melhores trabalhados em cursos mais avançados de estatística.
Primeiro, vamos padronizar a variável \(x\), utilizando a equação de conversão \(z=\frac{x-7}{1}\). Aplicando os limites \(x=4\) e \(x=9\) nessa equação, obtemos \(z=-3\) e \(z=2\).
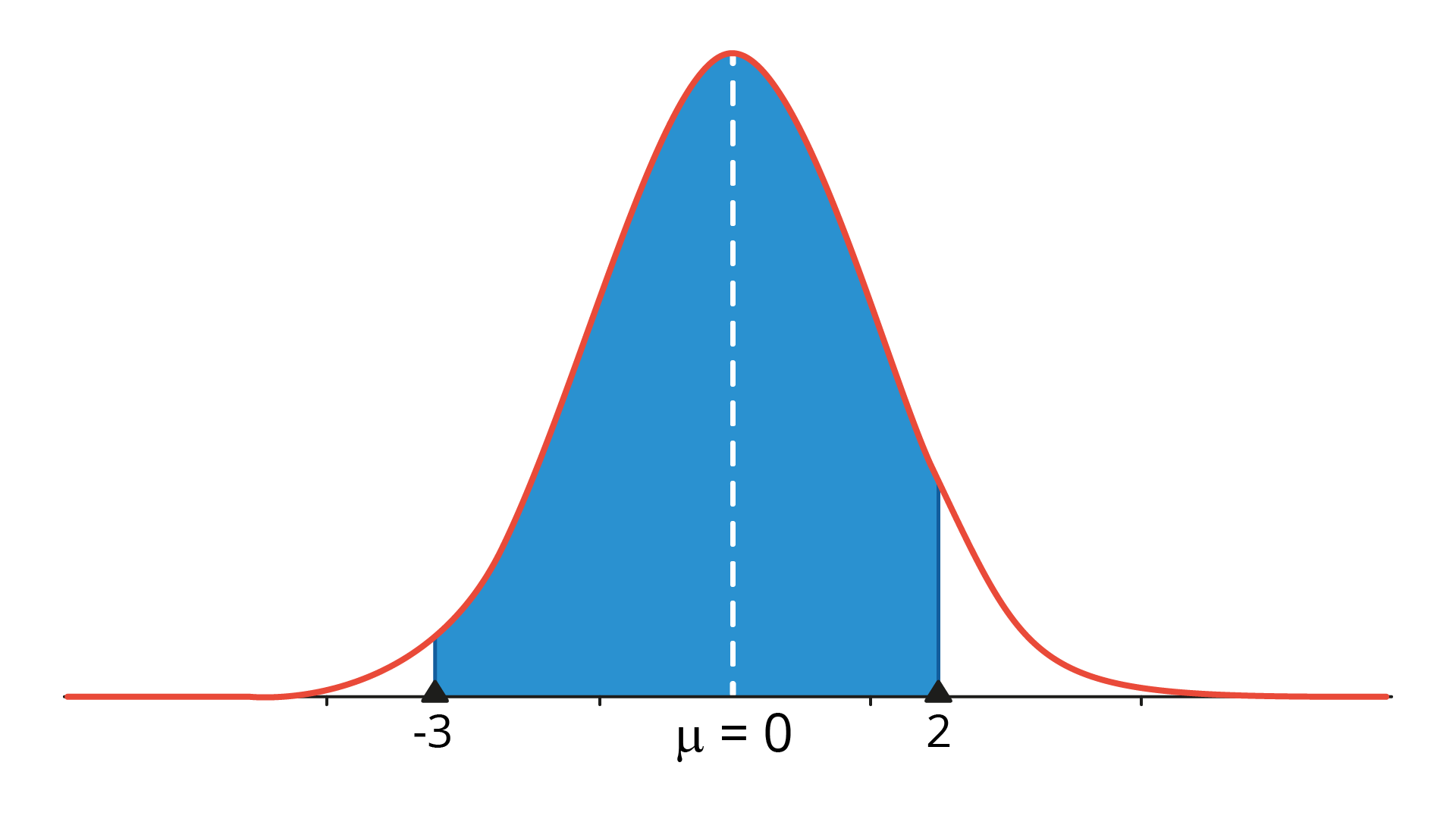
Por fim, vamos utilizar a tabela de escores \(z\) para determinação da probabilidade desejada:
\[P(4≤x≤9)=P(-3≤z≤2)=P(z≤2)-P(z≤-3)=0,9772-0,0013=0,9759\]
Portanto, 97,59% das câmaras frigoríficas atendem a legislação.
2) Em 2016 a China possuía uma média de 148,0 habitantes por \(k{{m}^{2}}\), com desvio-padrão de 32,0 hab/\(k{{m}^{2}}\). Assumindo que a distribuição de pessoas por área na China é normal, determine o percentual da área total do país com ocupação inferior a 115,1 hab./\(k{{m}^{2}}\).
Nas seções anteriores você aprendeu a calcular a área abaixo da curva normal situada à direita de um escore \(z\) predefinido. Nesta seção você aprenderá o processo inverso: determinar o escore \(z\) a partir de uma área conhecida. Para isso, considere o seguinte procedimento:
Por exemplo, suponha que queiramos determinar o escore \(z\) para o qual a área à esquerda de \(z\) seja igual a 0,6591. O primeiro passo para isso consiste em esboçar, em uma curva normal genérica, a área em questão e indicar a posição do escore \(z\) desejado. Essa etapa serve para visualizarmos se, de fato, o valor procurado pode ser lido diretamente na tabela (uma vez que esta só se refere a áreas acumuladas à esquerda).
Por fim, uma vez que tivermos a certeza que estamos em busca de uma área à esquerda de \(z\), procuramos na tabela o valor de 0,6591. Nesse caso encontramos que \(z=\)0,41.
A seguir, veja dois exercícios resolvidos que auxiliarão na sua compreensão desse procedimento.
Exercício resolvido 3 :
Determine o valor de \(a\) que torna a área indicada em lilás na figura a seguir igual a 0,7576.
Solução:
Observe que a região indicada em lilás corresponde à área delimitada entre os escores \(a\) e 0,75. Dessa forma, \(P\left( a\le z\le 0,75 \right)=0,7576\). Logo,
\[P\left( z\le 0,75 \right)-P\left( z\le a \right)=0,7576\]
\[0,7734-P\left( z\le a \right)=0,7576\]
\[-P\left( z\le a \right)=-0,0158\]
\[P\left( z\le a \right)=0,0158\]
Procurando na tabela de escores \(z\) o valor de \(0,0158\), concluímos que \(a=-2,15\).
Exercício Resolvido 4:
O comprimento de um fio de cobre, extraído de um determinado equipamento industrial, é, em média 3,2 metros, com desvio-padrão de 0,8 metros. Assumindo que o comprimento dos fios é normalmente distribuído, determine a dimensão mínima \(x\) para que 80% do conjunto de fios extraídos possuam comprimento inferior a \(x\).
Solução:
Inicialmente, vamos identificar na tabela o escore \(z\) para o qual a área acumulada à esquerda seja de 0,8. Assim, obtemos que \(z\simeq 0,85\).
Usando a equação \(z=\frac{x-\mu }{\sigma }\), convertendo o escore \(z\) para \(x\):
\[0,85=\frac{x-3,2}{0,8}\]
\[x-3,2=0,68\]
\[x=3,88~~~metros\]
Portanto, 80% dos fios produzidos pelo equipamento possuem comprimento inferior a 3,88 metros.
O quadro a seguir contempla um resumo do passo a passo para resolução de exercícios envolvendo a distribuição normal.
Com o Quadro 4.1, você pode inserir o passo a passo da coluna à esquerda toda vez que o exercício lhe fornecer um escore \(z\) e solicitar um valor de probabilidade. Para os exercícios que fornecem um valor de probabilidade, você deve proceder conforme passo a passo descrito na coluna da direita.
O nascimento do primeiro dente em um bebê é, em média, no 177º dia de vida da criança, tendo um desvio-padrão de 14 dias. Assumindo que essa idade segue uma distribuição normal, determine o número de dias mínimo para o qual, a partir dessa idade, 70% das crianças já tenham o seu primeiro dente.

Mario F. Triola
Editora: LTC
ISBN: 9788521622062
Comentário: Neste livro você encontrará outros exemplos e aplicações de todo o conteúdo trabalhado na unidade, além de inúmeros exercícios para fortalecer e fixar seu aprendizado.
Ano : 2015
Comentário : Esse vídeo contempla os principais tópicos do conteúdo da nossa unidade. Ele inicia tratando das principais características da Distribuição Normal. Em seguida, aborda as propriedades da curva Normal, incluindo a influência dos parâmetros média e desvio na geometria de tal curva. Por fim, orienta como realizar a padronização de uma curva Normal. Assista ao vídeo no link a seguir.
Aqui chega ao fim o conteúdo do seu curso básico de estatística. Agora você já pode se dizer conhecedor de todas as ferramentas básicas da estatística descritiva e da teoria das probabilidades. Pode, também, utilizar todo o conteúdo visto para realizar análise e tratativa de dados de forma assertiva e coerente quanto ao rigor científico exigido no ensino superior. Aproveite para fazer uma revisão de todo o conteúdo trabalhado no semestre, realizar todas as atividades práticas da disciplina e responder muitos exercícios até obter confiança quanto ao que aprendeu.
DEVORE, J. L. Probabilidade e estatística para engenharia e ciências . São Paulo: Pioneira Thomson Learning, 2006.
MONTGOMERY, D. C.; RUNGER, G. C. Estatística aplicada e probabilidade para engenheiros . Rio de Janeiro: LTC, 2003.
TRIOLA, M. F. Introdução à Estatística : atualização da tecnologia, v. único. 11. ed. Rio de Janeiro: LTC, 2013.