Fenômenos De Transporte
Conceitos Básicos
Nesta unidade, será feito um estudo inicial das características e propriedades dos fluidos, para que possamos compreender as principais diferenças entre o comportamento de líquidos e gases, e definiremos importantes conceitos como massa específica e densidade, por exemplo. Após isso, iniciaremos o estudo da estática dos fluidos, também chamada de hidrostática, o ramo dos fenômenos de transporte que estuda os fluidos em repouso. Esse campo da engenharia é muito utilizado no transporte de grandes cargas, como no caso dos elevadores hidráulicos, em que precisamos mover um peso do ponto A para o ponto B. Depois serão estudados os conceitos de tensão superficial e tangencial e do comportamento de fluidos submetidos a essas forças. Também iniciaremos o estudo da pressão que nos acompanhará em todo o estudo de fenômenos de transporte, porque fluidos produzem pressão na tubulação ou sofrem uma pressão para produzir o resultado que queremos. Finalmente, introduziremos o conceito de pressão nos fluidos homogêneos e heterogêneos e abordaremos a equação fundamental da estática dos fluidos. Essa equação, como o próprio nome nos diz, será muito utilizada nesta disciplina. Portanto, ao término desta unidade, o aluno será capaz de entender os conceitos introdutórios de fenômenos de transporte de maneira clara e precisa. Bons estudos.
Os gregos já acreditavam que tudo flui na natureza, ou seja, tudo se movimenta. Essa teoria, chamada de panta rei, que pode ser traduzida por “tudo flui”, equivale ao que hoje chamamos de fenômenos de transporte ou o estudo dos fluidos em movimento. Atualmente, uma das definições mais comuns sobre fenômenos de transporte é “o estudo de fatos da natureza que podem ser explicados cientificamente, nos quais um fluido é transportado”, e fluido é “uma substância que não tem forma própria, assume o formato do recipiente”, sendo caracterizado por um líquido ou um gás (BRUNETTI, 2008, p. 1). Sendo assim, um fluido tende a escoar quando manipulado ou a vazar quando não contido, como no caso dos gases.
Diante disso, essa área da engenharia está presente em uma ampla gama de aplicações que variam, desde o corpo humano, no qual as veias e artérias transportam nosso sangue com os nutrientes que necessitamos; no projeto de carros e espaçonaves, desde o transporte do combustível para o motor até como podemos vencer o atrito do ar; e até no mais básico dos itens que utilizamos para viver – a água, que é levada até nossa casa, por meio de um intrincado sistema de bombas e tubulações.
Os problemas causados devido aos fenômenos de transporte também serão nosso objeto de estudo. Dentre eles, destacamos a cavitação e o golpe de aríete ou até mesmo uma explosão em uma área classificada devido à presença de gás natural, por exemplo, em um projeto fora das normas técnicas.
Atualmente, temos áreas inovadoras em que as pesquisas se desenvolvem muito rapidamente, como a biomecânica (corações e válvulas artificiais e outros órgãos como o fígado) e o estudo de equipamentos para esportes amadores e de alto rendimento, além do estudo de fluidos inteligentes, como alguns que são utilizados na suspensão dos carros ou para ministrar doses precisas de remédios dentro do nosso corpo.
Em fenômenos de transporte, temos muitas características que devem ser utilizadas na compreensão de como um fluido se comporta em um escoamento. Essas características possuem uma simbologia específica que as representa e várias unidades que podem ser usadas para descrever sua medida. Isso já era feito na física, por exemplo, com o comprimento, cuja representação L podia ser feita em m, cm, mm e até mesmo polegadas. Agora, temos de fazer o mesmo para os conceitos relacionados a fluidos, como pressão, viscosidade etc.
Essas unidades se dividem em primárias, como o comprimento, tempo, massa e temperatura, e secundárias, como a velocidade, vazão, aceleração, área etc. Podemos escrever as unidades utilizando alguns sistemas de unidades diferentes. Os mais utilizados são o:
A Tabela 1.1, a seguir, apresenta alguns fatores de conversão do Sistema Britânico de Unidade para o SI:
Utilizamos no estudo de fenômenos de transporte leis fundamentais que relacionam as diversas grandezas da física com as propriedades dos fluidos. Os fluidos apresentam características diferentes dos sólidos, e as características dos líquidos podem diferir também das dos gases. Por exemplo, o petróleo cru vai escoar bem mais lentamente em uma tubulação do que se essa tubulação transportasse água. Agora, vamos começar a estudar essas características.
A massa específica de um fluido representada pelo símbolo ρ (lemos rô) é a massa do fluido por unidade de volume, e a equação é dada por:
ρ = \(\frac{m}{V}\) (Equação 1.1)
Em que sua unidade no SI (Sistema Internacional) é kg/m³.
A massa específica (ρ) dos líquidos é pouco sensível às variações de temperatura e pressão, enquanto a massa específica (ρ) dos gases é bastante influenciada tanto pela pressão quanto pela temperatura.
O peso específico de um fluido representado pelo símbolo \(\gamma\) (lemos gama) é o peso do fluido contido em uma unidade de volume, e a equação é dada por:
\(\gamma \) = \(\frac{G}{V}\) (Equação 1.2)
Onde G é o peso.
Como G = m . g, a relação entre peso e massa específica é deduzida de:
\(\gamma \) = \(\frac{G}{V}\)= \(\frac{m~.~g}{V}\Rightarrow \gamma \) = ρ. g (Equação 1.3)
Em que a unidade no SI (Sistema Internacional) é N/m³. Por exemplo, o peso específico da água a 15,6 ºC, considerando g = 9,807 m/s² é igual a 9,8 kN/m³ (MUNSON; YOUNG; OKIISHI, 2004, p. 11).
Muitas vezes, é dado o peso relativo para líquidos, simbolizado por \(\gamma \)\(r\) e definido por:
\(\gamma \)\(r\) = \(\frac{\gamma }{{{\gamma }_{\acute{a}gua}}}\) (Equação 1.4)
A densidade de um fluido, representada por SG (do inglês specific gravity, ou gravidade específica), é definida como a razão entre a massa específica do fluido e a massa da água a 4 ºC, adotada porque nessa temperatura ρ = 1.000 kg/m³.
SG = \(\frac{\rho }{{{\rho }_{\acute{a}gua}}}\). (Equação 1.5)
Muitos problemas fornecem o SG de um fluido e não sua massa específica. Assim, para um fluido com SG = 0,8, sua massa específica será igual a ρ = ρ \(_\text{água}\) . SG = 1.000 x 0,8 = 800 kg/m³.
Na Tabela 1.2, temos a massa específica, o peso específico e o peso relativo para diferentes tipos de fluidos.
Um reservatório está cheio de óleo para alimentar o sistema pneumático de uma indústria, cuja densidade é ρ = 850 kg/m³. Se o volume do reservatório é V = 2 m³, podemos determinar a quantidade de massa m nesse reservatório. A quantidade de massa m nesse reservatório será um número entre:
ÇENGEL, Y.; CIMBALA, J. M. Mecânica dos fluidos: fundamentos e aplicações. Tradução de K. A. Roque e M. M. Fecchio. Revisão técnica F. Saltara, J. L. Baliño e K. P. Burr. Consultoria Técnica H. M. Castro. São Paulo: McGraw-Hill, 2007. p. 18.
Já conhecemos as propriedades que indicam o peso do fluido, como a massa específica e a densidade. Essas propriedades não são suficientes para caracterizarmos o comportamento dos fluidos porque, por exemplo, a água e o óleo podem apresentar massas específicas aproximadamente iguais e apresentarem comportamento muito diferente quando escoam. Para isso, precisamos estudar as características de fluidez dos fluidos.
Quando aplicamos uma força de cisalhamento a um fluido, representado pela força P, na Figura 1.1, esse fluido irá se movimentar de maneira contínua com uma velocidade U, ou seja, o líquido irá se mover com uma velocidade que será função somente de u representada pelo gradiente de velocidade na Figura 1.1:
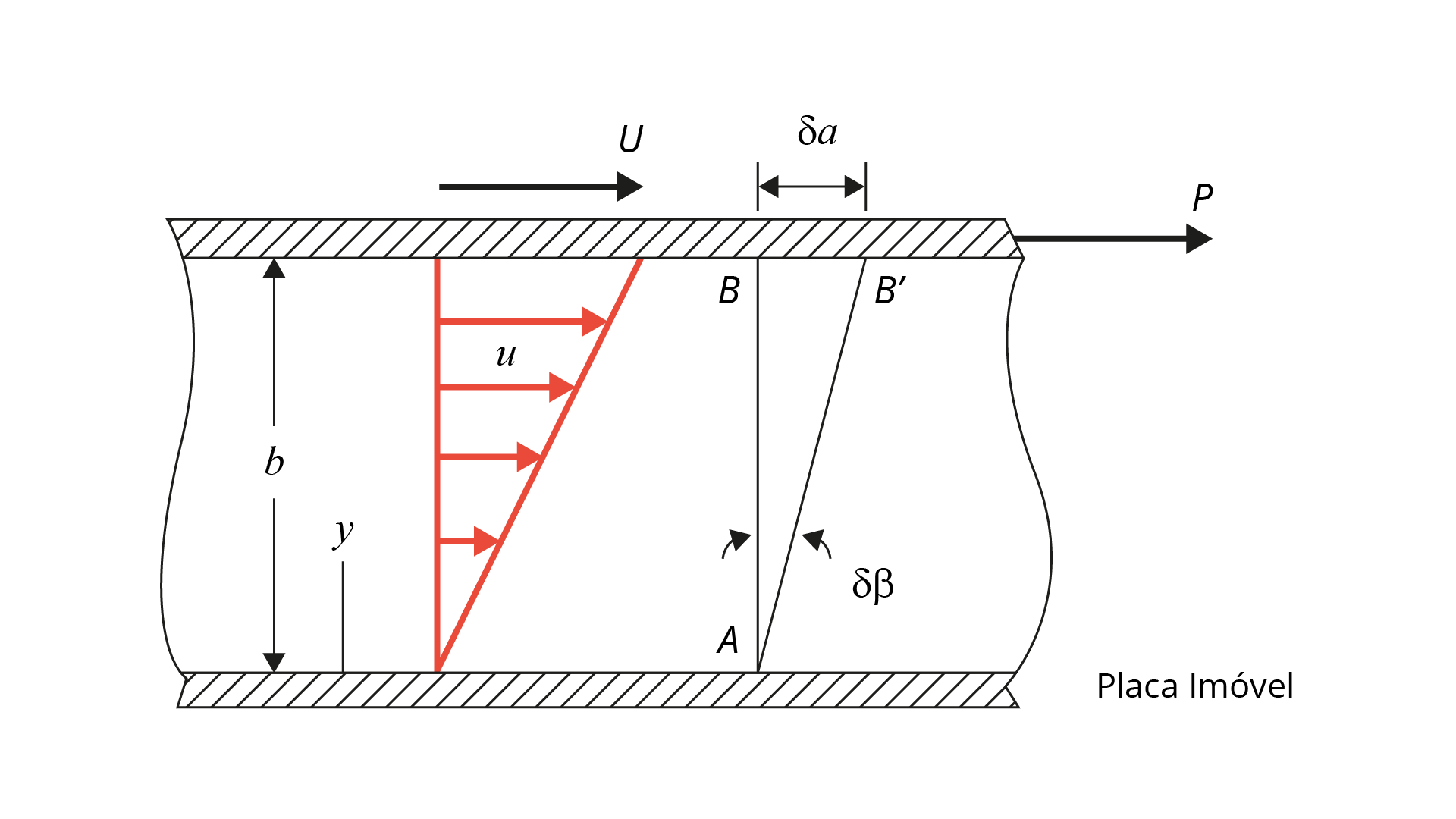
Em um pequeno intervalo de tempo, \(\delta \)t, uma linha vertical AB no fluido rotaciona um ângulo \(\delta \beta \)que será calculado pela equação:
tan \(\delta \beta \) = \(\delta \beta \) = \(\frac{\delta a}{b}\) (Equação 1.6)
Como \(\delta \)a = U \(\delta \)t, temos que
\(\delta \beta \) = \(\frac{U~\delta t}{b}\) (Equação 1.7)
Podemos observar que, como \(\delta \beta \)é função da força P e do tempo, essa taxa de variação com o tempo é definida como deformação de cisalhamento e representada pelo símbolo \(\tau \).
Na maioria dos fluidos, a tensão de cisalhamento é proporcional ao coeficiente de velocidade, representada por U na Figura 1.1, de onde temos a lei de Newton da viscosidade dada por
\(\tau \) \(\alpha \) \(\frac{du}{dy}\) (Equação 1.8)
Em que \(\alpha \) é um símbolo de proporcionalidade. Os fluidos que apresentam a tensão de cisalhamento proporcional ao coeficiente de velocidade são chamados de fluidos newtonianos, por obedecerem à lei descoberta por Newton. Esses fluidos apresentam uma relação linear, ou seja, a relação entre a tensão de cisalhamento e o coeficiente de velocidade é representada por uma reta. Esse coeficiente de proporcionalidade ficou conhecido como viscosidade, representado pelo símbolo \(\mu ~\)(lemos mi). A unidade da viscosidade no SI é N.s/m².
A viscosidade, representada pelo símbolo \(\mu ~\)(lemos mi), é a propriedade que indica se o fluido tem uma maior ou menor dificuldade de escoar, e ela varia, por exemplo, com a pressão e a temperatura.
Alguns exemplos de fluidos newtonianos são a água, o ar, os óleos etc. Já o sangue, as pastas de dentes, as tintas etc. não são classificados como fluidos newtonianos por apresentarem uma relação não linear, por exemplo, nos polímeros a viscosidade diminui enquanto a tensão de cisalhamento aumenta.
Ainda temos que, nos líquidos, a viscosidade diminui com o aumento da temperatura, enquanto, nos gases, a viscosidade aumenta com o aumento da temperatura.
Nesse contexto, a viscosidade dinâmica pode ser considerada como uma medida da resistência do fluido de se movimentar, correspondendo ao atrito interno gerado nos fluidos – devido às interações moleculares –, que, em geral, é uma função da temperatura.
A viscosidade cinemática representada pelo símbolo \(\upsilon \)(upsilon) é o quociente entre a viscosidade dinâmica e a massa específica, e pode ser expressa por:
\(\upsilon \) = \(\frac{\mu }{\rho }\) (Equação 1.9)
A unidade da viscosidade cinemática no SI é dada por \(m²/s\). Além disso, destacamos que o nome cinemática vem das unidades comprimento e tempo, duas das grandezas fundamentais da cinemática.
Durante o escoamento, um fluido pode sofrer uma pressão de vapor e uma tensão superficial. Essas tensões são importantes para explicarmos os diferentes comportamentos de um líquido e um gás quando estão submetidos a um deslocamento.
A água e a gasolina evaporam quando colocados em um ambiente ao ar livre. Essa evaporação ocorre porque algumas moléculas do líquido, localizadas perto da superfície livre do fluido, apresentam quantidade de movimento suficiente para superar as forças intermoleculares coesivas (forças que fazem com que essas moléculas se mantenham unidas) e escapem para a atmosfera.
Para projetarmos tubulações de uma maneira técnica e economicamente eficaz, temos de conhecer a pressão de vapor de um líquido, ou seja, qual o valor da mínima pressão que podemos ter na nossa tubulação antes que um líquido comece a evaporar. É claro que nunca impediremos essa evaporação totalmente, mas precisamos reduzi-la para evitar desperdícios.
Durante essa evaporação, aparecem bolhas de ar que se rompem quando entram em contato com uma tubulação metálica onde a pressão é maior. Esse efeito maléfico ao sistema pode atingir também bombas e turbinas hidráulicas. Ele é chamado de cavitação e pode causar grandes transtornos no funcionamento de um sistema hidráulico. A pá de uma turbina submetida à cavitação pode perder eficiência devido à redução da sua superfície de contato com o fluido, porque esse fenômeno vai desgastando o metal, sendo que o material danificado deve ser reposto por meio de uma manutenção.
Entre um líquido e um gás, conforme está mostrado na Figura 1.2, ou entre líquidos que não se misturam, aparece como que uma membrana na superfície de contato, chamada tensão superficial.
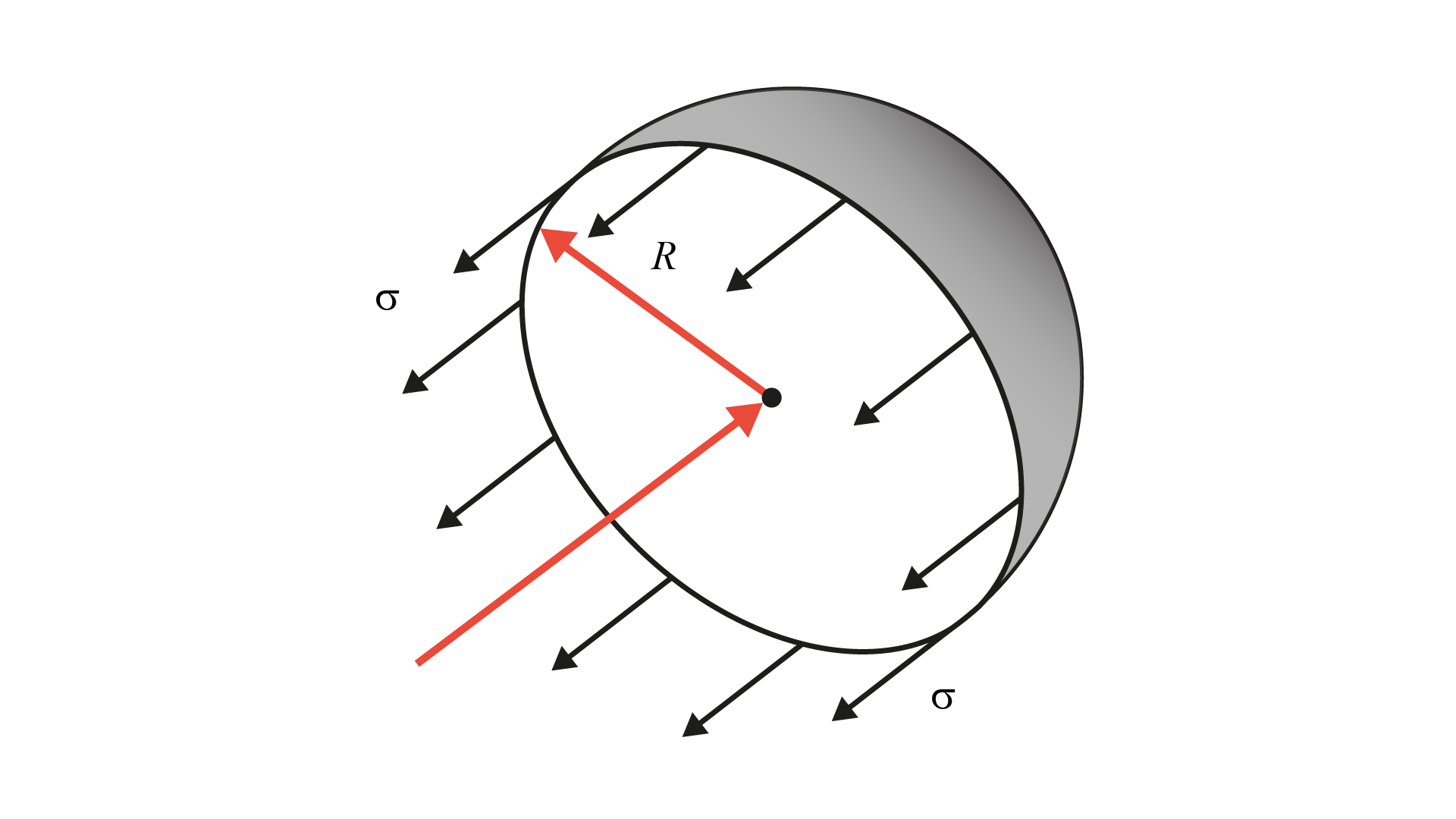
Por isso, são formadas gotas em uma superfície gordurosa, como ocorre quando a nossa pele é oleosa, por exemplo. Esse fenômeno ocorre porque um líquido é submetido a uma força diferente na superfície e no fundo do recipiente que o contém. Essa tensão é importante quando formos calcular como a água vai escoar no interior do solo em períodos chuvosos, por exemplo.
O ramo da mecânica dos fluidos que trata dos corpos em repouso é denominado estática, sendo que a dinâmica estuda os corpos em movimento. Na estática, a tensão, representada pela letra 𝜎 (lemos sigma), é definida como força por unidade de área, e pode ser dividida em dois tipos de tensão (normal e tangencial), conforme apresentado na Figura 1.3:
A tensão normal pode ser expressa por:
𝜎 = \(\frac{Fn}{A}\)(N/m2 = Pa) (Equação 1.10)
Em que a unidade é dada em N/m2, que equivale à unidade Pascal. Quando essa tensão é aplicada em um fluido em repouso, a tensão normal também pode ser denominada por pressão.
F\(_\text{n}\) = P (unidade Pascal) (Equação 1.11)
A força tangencial é também chamada tensão de cisalhamento 𝜏(lemos tau), e é dada por
τ =\(\frac{Ft}{A}\) (N/m2 = Pa) (Equação 1.12)
Os princípios da estática dos fluidos são utilizados no cálculo de forças sobre objetos submersos, como na análise da estabilidade de embarcações, no projeto de submarinos, na medição de pressão etc.
Com a definição da tensão de cisalhamento, podemos redefinir o fluido “como uma substância que não pode sustentar uma tensão de cisalhamento quando em repouso” (FOX et al., 2010, p. 27).
Para estudarmos os fenômenos de transportes, precisamos, na maioria das vezes, definir um volume no espaço por meio do qual o fluido escoa, e para fazer isso utilizamos o conceito de volume de controle. Desse modo, podemos estudar as turbinas, os compressores, as tubulações, os bocais etc. que constituem um sistema de transporte do fluido. Um volume de controle é um volume arbitrário no espaço através do qual o fluido escoa, e sua fronteira geométrica é denominada de superfície de controle, podendo ser real (no caso de tubulações) ou imaginária (como em rios). Já um sistema de controle pode ser aberto ou fechado.
Na Figura 1.4, temos um exemplo de um sistema de tubulação que apresenta exemplos físicos (como as tubulações e derivações) e exemplos imaginários (as entradas e saídas do fluido).

As cores das tubulações nos processos industriais nos indicam o fluido que estão transportando. As mais comuns são:
Além disso, é importante destacar que, nos edifícios, as tubulações em verde e em vermelho representam, respectivamente, os sistemas de abastecimento de água e os sistemas de combate a incêndio, as em amarelo, o sistema de gás, e as em cor-de-alumínio, o sistema de gás liquefeito.
Um fluido ideal é utilizado para simular um escoamento sem perdas por atrito, um escoamento com viscosidade zero. Esse fluido é utilizado para entendermos a equação de Bernoulli, que trata da conservação de energia em um escoamento fluido.
Dizemos que um fluido é incompressível quando “seu volume não varia ao modificarmos a pressão sobre ele”, ou seja, sua massa específica não varia com a pressão” (BRUNETTI, 2008, p. 10).
Sendo assim, esse comportamento pode ser aplicado para líquidos e gases no estudo da ventilação.
Uma pressão de 88 Pa deve ser aplicada à válvula de uma comporta, conforme a figura a seguir, para que ela permaneça na posição fechada. A força normal exercida por essa pressão está situada no intervalo entre:
Assinale a alternativa correta:
A pressão é uma força exercida sobre uma unidade de área que pode realizar um trabalho no transporte de cargas pesadas, como no caso dos elevadores hidráulicos.
A pressão nada mais é do que a tensão normal dividida pela área de aplicação dessa força. Matematicamente, temos:
p = \(\frac{Fn}{A}\)(N/cm2) (Equação 1.13)
Devemos ter em mente que pressão e força são conceitos diferentes. Por exemplo, podemos ter uma força de 1 N aplicada em uma área de 10 ou 5 cm². A força será a mesma, mas a pressão, não. As pressões serão iguais a 0,1 e 0,2 N/cm², respectivamente, ou seja, quanto maior a área em que a força é exercida, menor é a pressão.
A diferença de pressão entre dois pontos de um fluido em repouso é igual ao produto do peso específico do fluido pela diferença de cotas dos dois pontos. Esse teorema é a explicação para o aumento de pressão conforme mergulhamos. A pressão na superfície, ao nível do mar, é menor do que a uma profundidade de 20 m, por exemplo. Matematicamente, essa lei pode ser escrita como:
\(\frac{dP}{dz}\) = - ρ g (Equação 1.14)
Essa equação também é conhecida como a equação fundamental da estática dos fluidos.
Podemos realizar um experimento simples para demonstrar o teorema de Stevin. Para isso, basta fazermos perfurações perto da tampa e embaixo, perto do fundo, em uma garrafa de refrigerante cheia de água, que está ilustrada na Figura 1.5, para constatarmos que os furos inferiores escoam a água com jatos mais potentes do que os furos superiores.

Devemos ressaltar que a diferença de pressão entre dois pontos quaisquer é igual ao produto do peso específico do fluido, multiplicado pela diferença de cotas entre esses pontos, não importando:
A pressão aplicada em um ponto de um fluido em repouso é transmitida integralmente a todos os pontos do fluido. Se a pressão aplicada é distribuída integralmente em todos os pontos do fluido, podemos amplificar ou reduzir a força aplicada, diminuindo ou aumentando a área de aplicação dessa força, respectivamente. Portanto, esse é o princípio do elevador hidráulico, que está ilustrado na Figura 1.6:
Utilizamos a pressão para indicar a força normal atuando sobre um ponto por unidade de área atuando sobre um fluido em um dado plano. Considerando o diagrama de corpo livre mostrado na Figura 1.7, construímos essa figura removendo um pequeno elemento do fluido, com a forma de uma cunha triangular. Para facilitar a visualização, não mostramos as forças na direção x e o eixo z foi referenciado como vertical (por causa da atuação do peso). Analisaremos primeiro o fluido em movimento acelerado para chegarmos à sua análise em repouso.
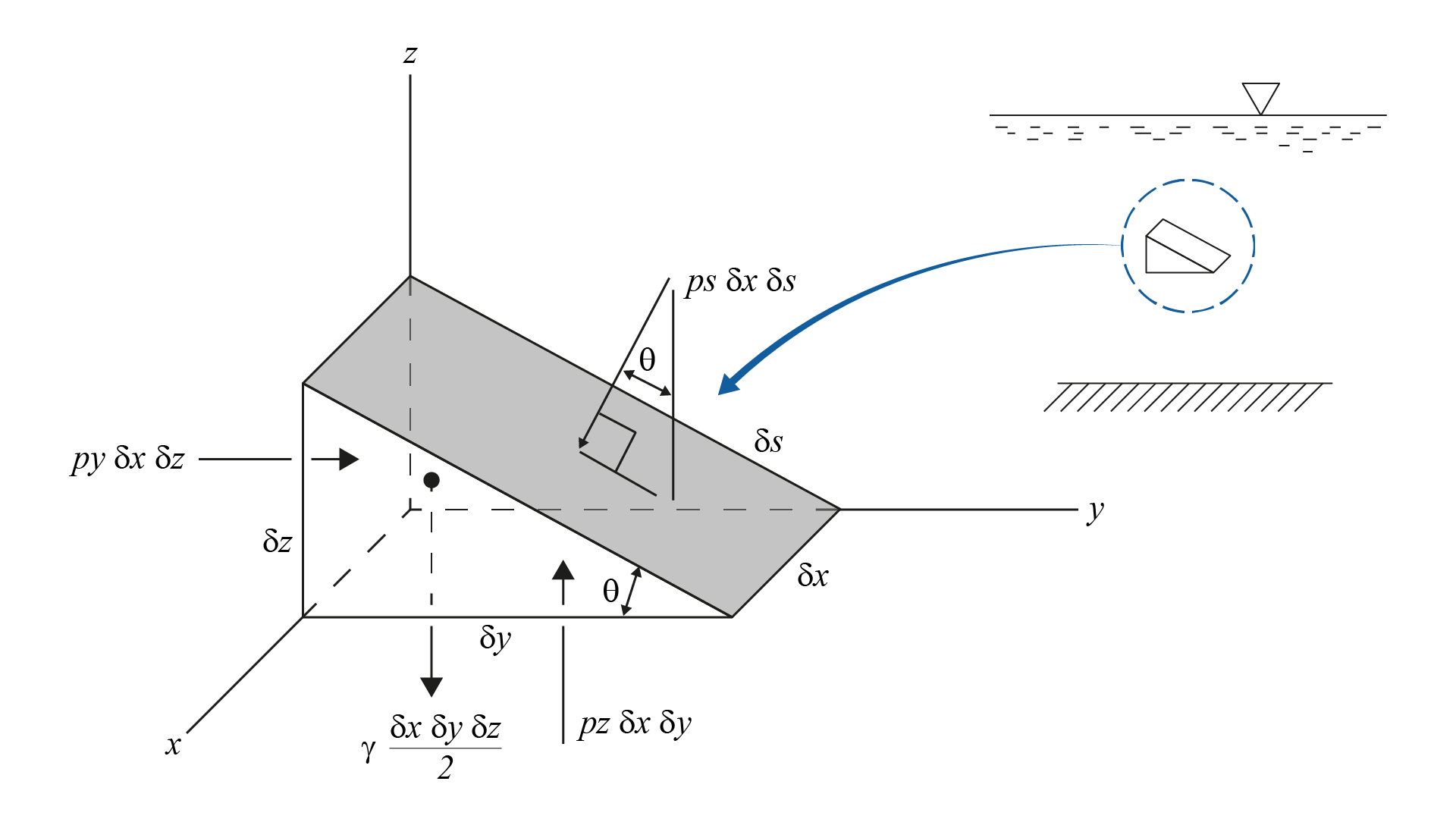
As equações do movimento (2ª Lei de Newton) nas direções y e z serão dadas por:
\(\sum F_y=p_y~\delta x \delta z - p_s~\delta x \delta s~~sen \theta = \rho \frac{ \delta x \delta y \delta z}{2} a_y\) (Equação 1.15)
\(\sum F_z=p_z~\delta x \delta y - p_s~\delta x \delta s~~cos \theta - \gamma \frac{ \delta x \delta y \delta z}{2}= \rho \frac{ \delta x \delta y \delta z}{2} a_z\) (Equação 1.16)
\(\mathop{\sum }_{{}}^{{}}{{F}_{z}}\)= pz \(\delta x\delta \)z - ps \(\delta x\delta \)s cos \(\theta \) - \(\gamma ~\frac{\delta x~\delta y~\delta z}{2}\) = \(\rho ~\frac{\delta x~\delta y~\delta z}{2}\)az (Equação 1.16)
onde:
A pressão necessita ser multiplicada por uma área para obtermos a força gerada por ela. Ao analisarmos a geometria da cunha, constatamos que:
Podemos estender este raciocínio para a equação (1.15), onde:
\( \sum F_y=p_y~\delta x \delta z – p_s \delta x \delta s~~sen \theta=\rho \frac{ \delta x \delta y \delta z}{2} a_y\)
Como \( \delta z = \delta s~sen \theta\)
\(p_y \delta x \delta z – p_s \delta x \delta s = \rho~a_y \frac{ \delta x \delta y \delta z}{2}\)
Cancelando \(\delta x \delta z\) e sabendo que \(\frac{\delta z}{2}→0\)
\(p_y=p_s\)
Para a equação (1.16) temos que
\( \sum F_y=p_z~\delta x \delta y – p_s \delta x \delta s~~cos \theta-\gamma \frac{ \delta x \delta y \delta z}{2}\)
Como \(\delta y = \delta s cos \theta\) e \(\gamma= \rho~a_z\)
Então \(\sum F_y= p_z \delta x \delta y – p_s \delta x \delta y - \rho~a_z \frac{ \delta x \delta y \delta z}{2}\).
Então
\(p_z~\delta x \delta y – p_s \delta x \delta y - \rho~a_z \frac{ \delta x \delta y \delta z}{2}=\)
\(p~z~dx~dy-p~s~dx~dy=\rho~a_z \frac{ \delta x \delta y \delta z}{2}\)
Cancelando \(dx\) \(dy\)
\(P~z-p~s=\rho~a_z \frac{\delta z}{2}\)
E como \(\frac{\delta z}{2}→ 0\)
\(p_z-p_s=0\)
Logo \(p_z=p_s\)
Ou seja, como \(\delta y = \delta s~ cos \theta\) e \(\delta z = \delta s~sen \theta\) (Equação 1.17)
Então, podemos escrever as equações do movimento como sendo:
\(p_y - p_s = \rho a_y \frac{\delta y}{2}\) (Equação 1.18)
\(p_z - p_s = (\rho a_z + \gamma ) \frac {\delta z}{2}\) (Equação 1.19)
Para um ponto, vamos analisar o limite onde x, y e z tendem a zero e vamos manter constante. Logo,
\(p_y = p_s e p_z = p_s\) (Equação 1.20)
Então, \(p_s = p_y = p_z\). Podemos concluir que a pressão em um ponto de um fluido em repouso, ou em um movimento no qual as tensões de cisalhamento não existem, é independente da direção, ou seja, essa é a demonstração do teorema de Pascal.
Consideremos um elemento do fluido como o mostrado na Figura 1.8. Nesse elemento, atuam dois tipos de forças: as superficiais devidas à pressão, e as de campo que, nesse caso, é igual ao peso do elemento. Se chamarmos a pressão no centro geométrico por p, as pressões médias nas várias faces do elemento podem ser expressas em função de p e de suas derivadas (conforme está retratado na Figura 1.8). A força resultante na direção y é dada por:
\(\delta \)Fy = \(\left( p~-~\frac{dp}{dy}~\frac{\delta y}{2} \right)\delta \)x \(\delta \)z - \(\left( p~+~\frac{dp}{dy}~\frac{\delta y}{2} \right)\delta \)x \(\delta \)z (Equação 1.21)
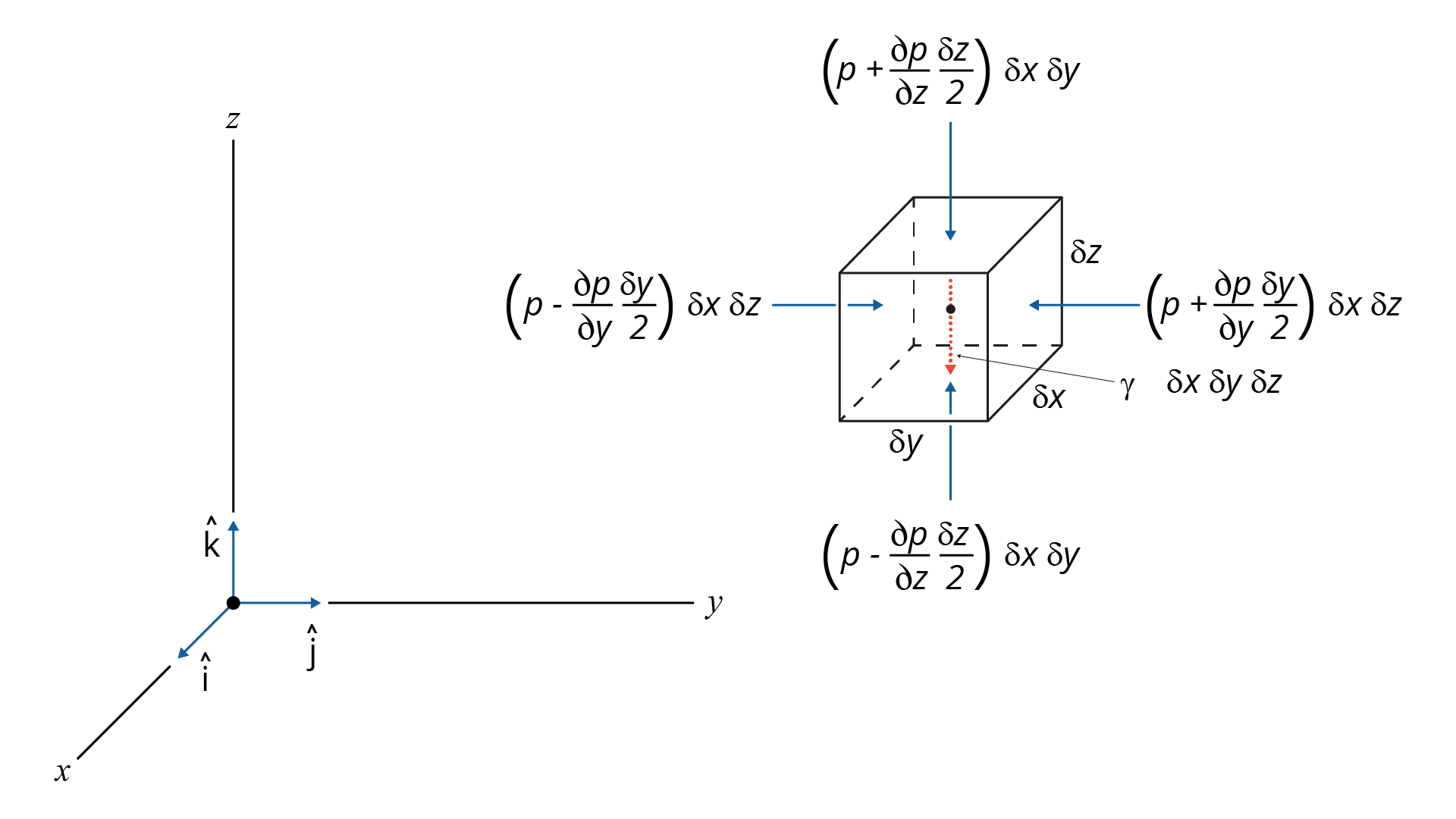
Reescrevendo a Equação 1.21, temos que:
δFy = - \(\frac{dp}{dy}\)δx δy δz (Equação 1.22)
Da mesma forma, as forças resultantes nas direções x e z serão obtidas das equações:
δFx = - \(\frac{dp}{dx}\)δx δy δz e δFz = - \(\frac{dp}{dz}\)δx δy δz (Equação 1.23)
A força vetorial da força superficial resultante que atua no elemento é:
δFs = δFx \(\hat{i}\) + δFy \(\hat{j}\) + δFz \(\hat{k}\) (Equação 1.24)
Reescrevendo novamente, temos que:
δFs = - \(\left( \frac{dp}{dx}~\widehat{i~}~+~\frac{dp}{dy}~\hat{j}~+~\frac{dp}{dz}~\hat{k} \right)\delta \)x δy δz (Equação 1.25)
onde \(\widehat{i~}\), \(\widehat{j~}\) e \(\widehat{k~}\) são vetores unitários do sistema de coordenadas da Figura 1.89.
O grupo entre parênteses da Equação 1.25 representa a forma vetorial do gradiente de pressão e pode ser reescrito como:
\(\frac{dp}{dx}~\widehat{i~}~+~\frac{dp}{dy}~\hat{j}~+~\frac{dp}{dz}~\hat{k}\) = ᐁp (Equação 1.26)
sendo que:
ᐁ( ) = \(\frac{d\left( ~~ \right)}{dx}~\widehat{i~}~+~\frac{d\left( ~~ \right)}{dy}~\hat{j}~+~\frac{d\left( ~~ \right)}{dz}~\hat{k}\) (Equação 1.27)
e o símbolo ᐁ representa o operador gradiente. Assim, a força superficial por unidade de volume pode ser expressa por
\(\frac{\delta {{F}_{s}}}{\delta x~\delta y~\delta z}\)= - ᐁp (Equação 1.28)
Como o eixo z é vertical, o peso do elemento de fluido que estamos analisando é dado por
- δW \(\hat{k}\) = - \(\gamma \)δx δy δz \(\hat{k}\) (Equação 1.29)
O sinal negativo indica que a força devida ao peso aponta para baixo (sentido negativo do eixo z).
Agora, vamos aplicar a 2ª Lei de Newton no fluido:
\(\mathop{\sum }_{{}}^{{}}\delta F\)= δm a (Equação 1.30)
onde \(\mathop{\sum }_{{}}^{{}}\delta F\)representa a força resultante que atua no elemento, a é a aceleração do elemento e δm é a massa do elemento (que pode ser escrita como \(\rho \gamma \delta \)x δy δz). Desse modo, a Equação 1.30 resulta em:
\(\mathop{\sum }_{{}}^{{}}\delta F\)= δFs - δW \(\hat{k}\) = δm a (Equação 1.31)
ou
- ᐁp δx δy δz - \(\gamma \) δx δy δz \(\hat{k}\) = ρ δx δy δz a (Equação 1.32)
Dividindo a Equação 1.21 por δx δy δz, obtemos:
- ᐁp - \(\gamma \hat{k}\) = ρa (Equação 1.33)
A Equação 1.33 é chamada equação geral do movimento. Ela é válida para os casos em que as tensões de cisalhamento no fluido são nulas. Ela será muito utilizada para calcularmos a pressão nos fluidos em movimento.
Geralmente o sistema de abastecimento de uma cidade capta a água de um rio, riacho ou córrego
perto da cidade onde é realizado o tratamento desta água dentro dos padrões estabelecidos por normas,
como o valor do flúor que deve ser injetado na água para que a mesma possa ser então distribuída.
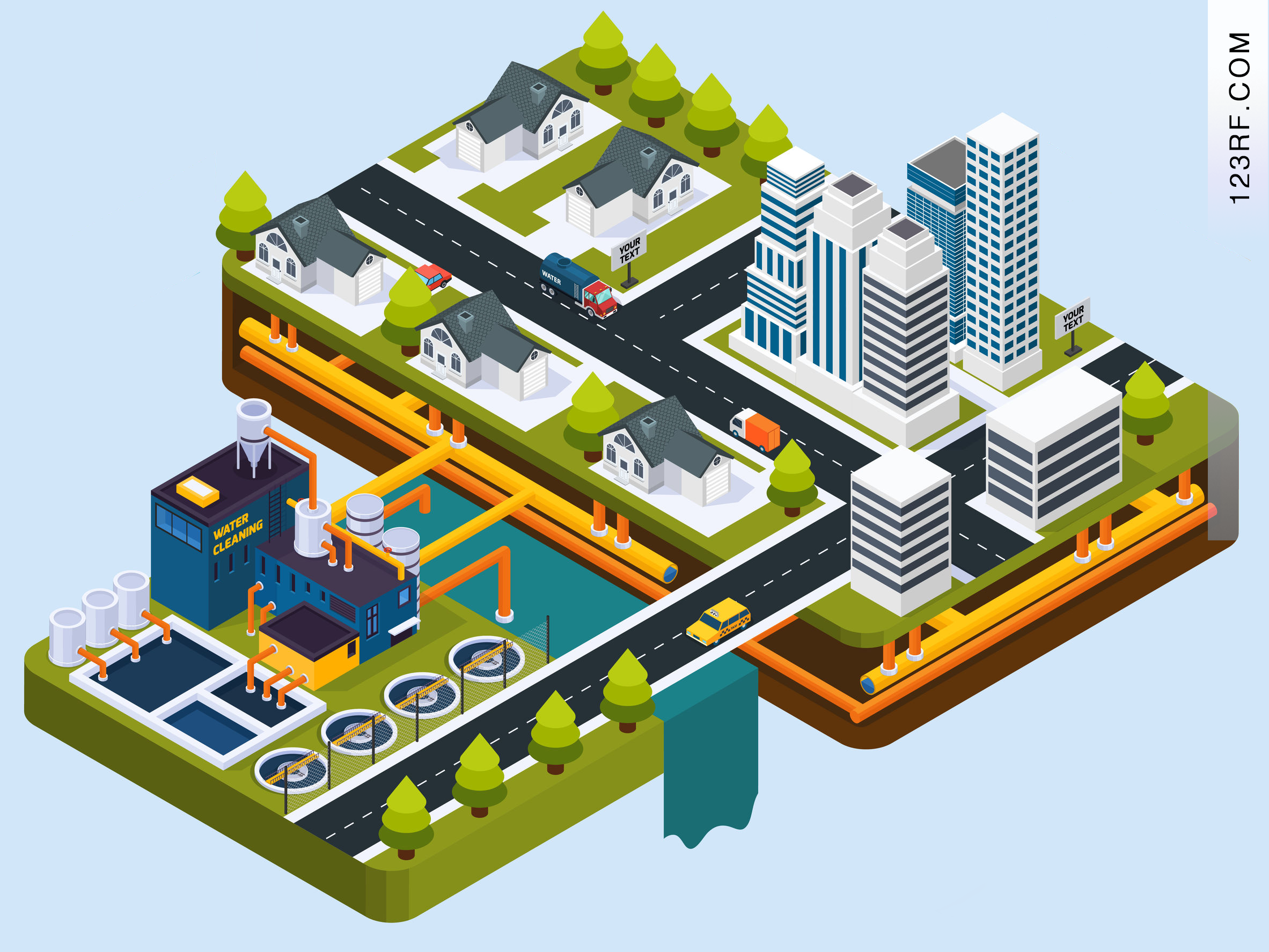
A água é levada até às nossas casas através de tubulações, bombas e caixas d’água. Na maioria das
vezes o sistema de distribuição funciona somente por gravidade, mas em lugares onde isto não é possível temos que instalar bombas.

As válvulas ajudam o sistema a regular o fluxo da água permitindo que no horário de maior consumo o fluxo seja maior e no horário de menor consumo o fluxo seja menor para evitarmos perda de água nas
tubulações devido aos vazamentos.
Deste modo a água chega na nossa casa em condições próprias para consumo.

Quando um fluido está em repouso, a aceleração é nula (a = 0 m/s²). O gradiente de pressão se reduz a
- ᐁp - \(\gamma \hat{k}\) = 0 (Equação 1.34)
Os componentes da Equação 1.34 são:
\(\frac{dp}{dx}\)= 0 \(\frac{dp}{dy}\)= 0 \(\frac{dp}{dz}\)= - \(\gamma \) (Equação 1.35)
Essas equações mostram que a pressão não é função de x ou de y. Assim, não detectamos qualquer variação no valor da pressão quando mudamos de um ponto para outro situado no mesmo plano horizontal. Logo, a equação de p se torna:
\(\frac{dp}{dz}= - \gamma\) (Equação 1.36)
A Equação 1.36 é de fundamental importância para o cálculo da distribuição de pressão nos casos em que o fluido está em repouso e pode ser utilizada para determinar como a pressão varia com a elevação. Essa equação indica que o gradiente de pressão na direção vertical é negativo, ou seja, a pressão decresce quando nos movemos para cima em um fluido em repouso. Essa equação é uma comprovação do teorema de Stevin.
A variação do peso específico de um fluido é provocada pelas variações de sua massa específica e da aceleração da gravidade. Isso ocorre porque \(\gamma \) é igual ao produto da massa específica do fluido pela aceleração da gravidade (\(\gamma \) = ρ g, peso específico N/m³). Como a variação de g não será considerada neste estudo, vamos analisar somente as variações de ρ (massa específica, kg/m³). A variação de massa específica dos líquidos normalmente pode ser desprezada. Nos casos em que a hipótese de peso específico é constante, a Equação 1.36 pode ser integrada diretamente, resultando em:
\(\int\limits_{p_1}^{p_2}dp=- \gamma \int\limits_{z_1}^{z_2}dz\) (Equação 1.37)
onde p1 e p2 são as pressões nos planos com cota z1 e z2, conforme é mostrado na Figura 1.9:
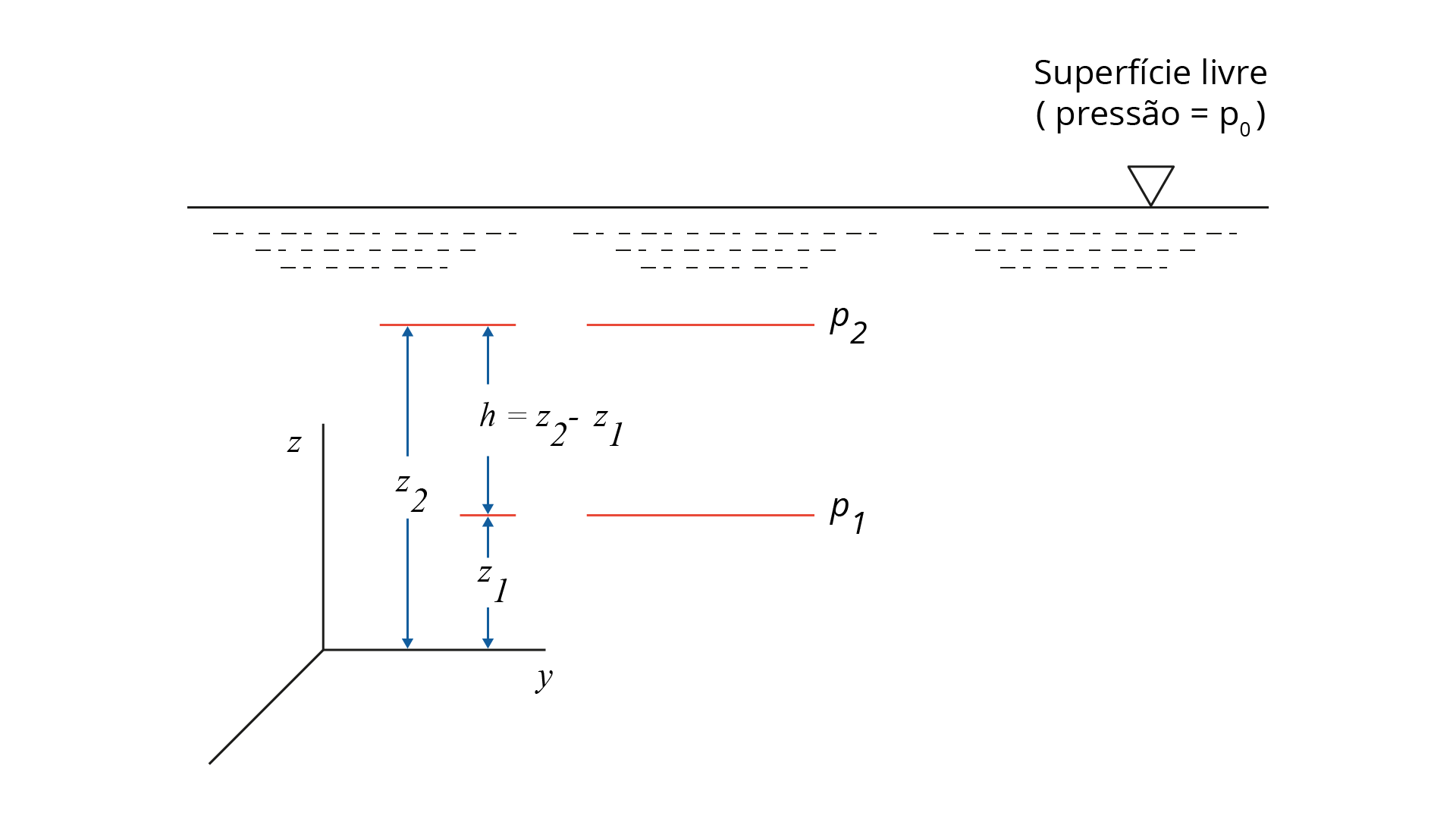
A Equação 1.37 pode ser reescrita como:
\(p_1- p_2 = 𝛾 (z_2 - z_1)= 𝛾 h\)
(Equação 1.38)
onde h é igual a distância z2 - z1 (profundidade medida a partir do plano que apresenta p2). A Equação 1.38 mostra que a pressão em um fluido incompressível em repouso varia linearmente com a profundidade. Essa distribuição de pressão é chamada de pressão hidrostática. Essa equação também comprova o teorema de Stevin.
Da Equação 1.38 temos que a diferença de pressão entre dois pontos pode ser especificada pela distância h, ou seja:
\(h = \frac{{{p}_{1}}~-~{{p}_{2}}}{\gamma }\) (Equação 1.39)
Sendo que h é chamada de carga e é interpretada como a altura da coluna de fluido com peso específico \(\gamma \) necessário para provocar uma diferença de pressão p1 - p2. A pressão p\(_0\) é utilizada para nos referirmos à pressão atmosférica e, muitas vezes, é representada por uma superfície livre.
A distribuição de pressão em um fluido homogêneo, incompressível e em repouso é função apenas da profundidade (em relação a um plano de referência), e ela não é influenciada pelo tamanho ou forma do tanque ou recipiente que contém o fluido. Pela aplicação da Equação 1.39, temos que a pressão será a mesma em todos os pontos da linha AB da Figura 1.10. O valor real da pressão ao longo da linha AB depende apenas da profundidade, h, da pressão na superfície livre, p\(_0\) e do peso específico do fluido contido no reservatório.
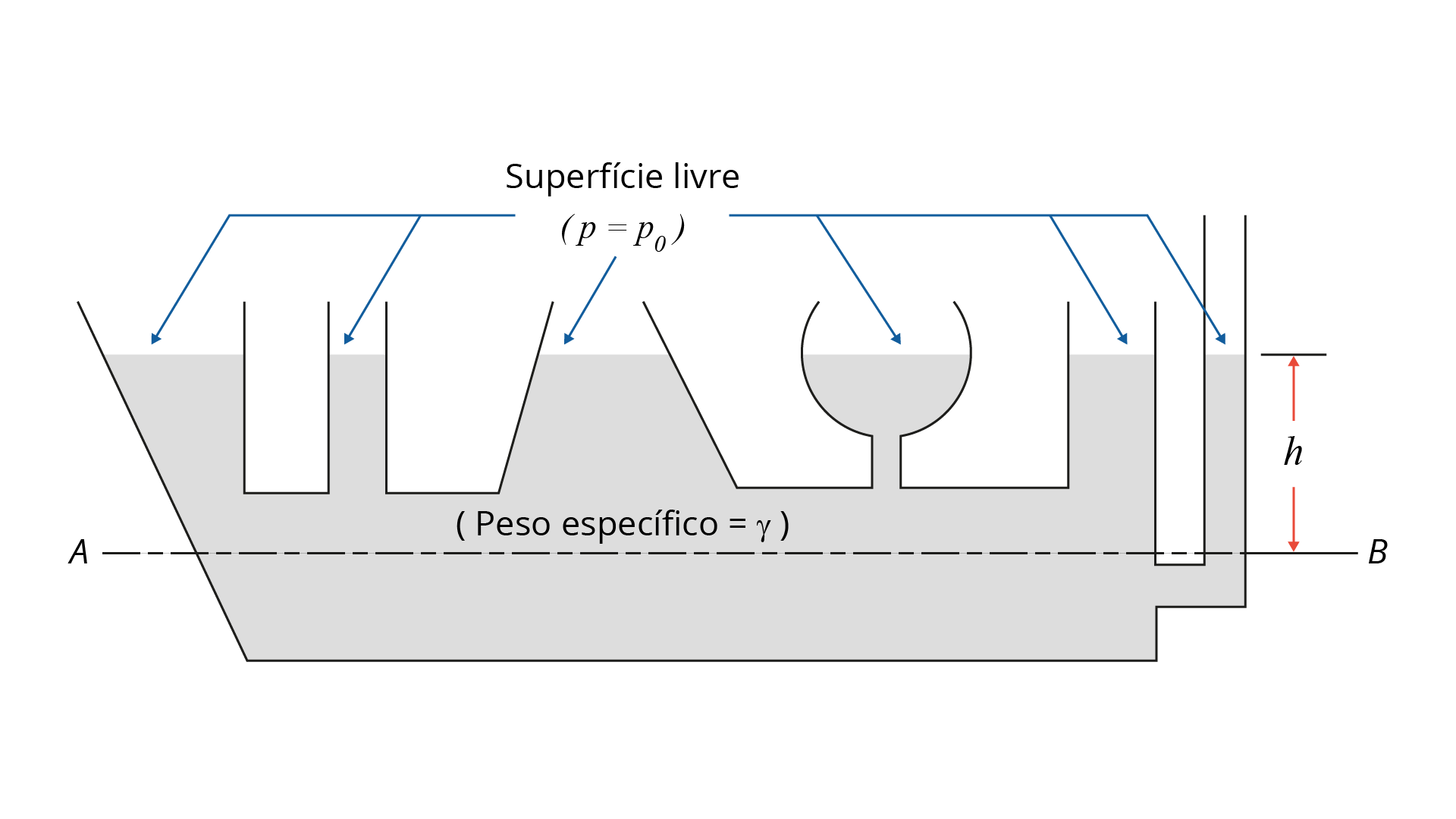
O fato de a pressão ser constante em um plano com mesma elevação é fundamental para a operação de dispositivos hidráulicos, como macacos, prensas, controles de aviões e de máquinas pesadas.
Os fenômenos de transporte são fundamentais no nosso dia a dia. Graças a eles, temos água nas nossas casas. Com as mudanças climáticas, está ficando cada vez mais difícil o abastecimento de água nas grandes cidades. Com o aquecimento global, esse fenômeno pode se agravar, demandando projetos cada vez com menores perdas e mais eficientes. Será que no futuro um país poderá desperdiçar água com vazamentos em suas tubulações como ocorre com 30% da água tratada no Brasil?
Fonte: Cirilo (2015).
Os gases, como o oxigênio e o nitrogênio, são modelados como fluidos compressíveis porque suas massas específicas variam de modo significativo com as alterações de temperatura e pressão. Por isso, temos de considerar a possibilidade da variação do peso específico do fluido antes de integrarmos a Equação 1.31. Na maioria das vezes, essa aproximação não precisa ser feita porque o gradiente de pressão do ar é muito pequeno quando comparado com o dos líquidos. Só a título de ilustração, o peso específico do ar ao nível do mar a 15 ºC é 1,2 x 10¹ N/m³, enquanto que o da água, nas mesmas condições, é de 9,8 x 10³ N/m³.
Se tivermos de considerar a variação do peso específico devido a uma grande diferença de altura, da ordem de milhares de metros, devemos considerar a variação do peso específico do fluido nos cálculos das variações de pressão por meio da fórmula:
p = ρ R T (Equação 1.40)
onde R é a constante do gás e T é a temperatura absoluta (em Kelvin).
Combinando as Equações 1.40 com a Equação 1.37, temos que
\(\frac{dp}{dz}\) = - \(\frac{g~p}{R~T}\) (Equação 1.41)
Separando as variáveis, ficamos com
\(\mathop{\int }_{{{p}_{1}}}^{{{p}_{2}}}dp\) = ln \(\frac{{{p}_{1}}}{{{p}_{2}}}\) = - \(\frac{g~}{R}\mathop{\int }_{{{z}_{1}}}^{{{z}_{2}}}\frac{dz}{T}\) (Equação 1.42)
onde g e R foram admitidos constantes no intervalo de integração.
O artigo sobre “Abordagem didática e prática da ação do vento em edificações”, apresentado na ConstruMetal de 2016, trata de uma forma simples e precisa sobre os cuidados que devemos tomar nos projetos de grandes edifícios, devido à pressão que a força do vento exerce nos andares superiores.
Também podemos utilizar a expressão
p2 = p1 exp \(\left[ -~\frac{g~\left( {{z}_{2}}~-~{{z}_{1}} \right)~}{R~{{T}_{0}}} \right]\) (Equação 1.43)
A Equação 1.43 fornece a relação entre a pressão e a altura numa camada isotérmica de um gás perfeito. Para tubulações de gases, como a de gás natural, esse efeito não precisa ser considerado, porque as distâncias verticais envolvidas no projeto são pequenas.
A figura a seguir apresenta esquematicamente uma prensa hidráulica, em que os dois êmbolos têm, respectivamente, as áreas A1 = 10 cm² e A2 = 100 cm².
BRUNETTI, F. Mecânica dos fluidos. 2. ed. rev. São Paulo: Pearson Prentice Hall, 2008.
Considerando que uma força de 200 N seja aplicada no êmbolo (1), assinale a alternativa que indica qual será a força transmitida ao (2).

Ano: 2016
Comentário: essa é a história da plataforma de extração de petróleo no Golfo do México que, por vários motivos, explodiu e foi responsável pelo maior desastre ambiental daquela região. A reconstrução da plataforma, a tubulação de extração do petróleo e a pressão com que o acidente ocorre são aspectos imperdíveis.

Yunus A. Çengel e John M. Cimbala
Editora: McGraw-Hill
Comentário: o livro indicado traz muitas aplicações novas para a área de mecânica dos fluidos. Cada capítulo apresenta um estudo de caso relacionado a uma preocupação ambiental como a geração de energia eólica, os transplantes de órgãos e a aerodinâmica dos carros.
Chegamos ao final do estudo dos conceitos fundamentais para o entendimento dos fenômenos de transporte. Nesta unidade, estudamos as propriedades dos fluidos, como a massa específica e, inclusive, os vários sistemas de unidades que podemos utilizar.
Depois iniciamos o estudo da estática dos fluidos, em que aprendemos que fluidos são líquidos e gases e que a estática é a parte da ciência que estuda os líquidos em repouso.
Vimos, também, que a viscosidade é uma propriedade fundamental dos fluidos. Cada fluido tem uma determinada viscosidade que apresenta importância fundamental no projeto de tubulações e de equipamentos como os elevadores hidráulicos.
Também estudamos o conceito de pressão e a variação da pressão com a posição em líquidos homogêneo e heterogêneo.
E, finalmente, aprendemos a equação fundamental da estática dos fluidos, com um exemplo ilustrativo.
BRAGA FILHO, W. Fenômenos de transporte para engenharia. 2. ed. São Paulo: LTC, 2012.
BRUNETTI, F. Mecânica dos fluidos. 2. ed. rev. São Paulo: Pearson Prentice Hall, 2008.
CIRILO, J. A. Crise hídrica: desafios e Superação. Revista USP, São Paulo, n. 106, p. 45-58, jul./ago./set. 2015. Disponível em: https://www.revistas.usp.br/revusp/article/download/110102/108685/. Acesso em: 20 dez. 2019.
ÇENGEL, Y.; CIMBALA, J. M. Mecânica dos fluidos: fundamentos e aplicações. Tradução de K. A. Roque e M. M. Fecchio. Revisão técnica F. Saltara, J. L. Baliño e K. P. Burr. Consultoria Técnica H. M. Castro. São Paulo: McGraw-Hill, 2007.
FOX. R. W. et al. Introdução à mecânica dos fluidos. 8. ed. Tradução e revisão técnica R. N. Koury. São Paulo: LTC, 2010.
HIBBELER, R. C. Mecânica dos fluidos. Tradução de D. Vieira. São Paulo: Pearson Education do Brasil, 2016.
MUNSON, B. R.; YOUNG, D. F.; OKIISHI, T. H. Fundamentos da mecânica dos fluidos. Tradução da quarta edição americana de Euryale de Jesus Zerbini. São Paulo: Edgard Blucher, 2004.
NASCIMENTO, B. M.; MORATTI, D. G.; OLIVEIRA JR., J. L.; SCOTÁ, N. M., BROETTO, R. B.; SAGRILO, R. G.; FERREIRA, W. G. Abordagem didática e prática da ação do vento em edificações. In: CONGRESSO LATINO-AMERICANO DA CONSTRUÇÃO METÁLICA, 7., 2016, São Paulo. Anais [...]. São Paulo: ABCEM, 2016. Disponível em: https://www.abcem.org.br/construmetal/downloads/Anais-do-7-Construmetal2016-EBook.pdf. Acesso em: 23 dez. 2019.