Laboratório de Matemática e Física
Noções introdutórias, Funções afins e Movimento Retilíneo Uniforme
Laboratório de Matemática e Física
Noções introdutórias, Funções afins e Movimento retilíneo uniforme
Nesta unidade, o leitor inicialmente irá aprender a trabalhar com o sistema de coordenadas cartesianas de modo a localizar espacialmente pontos no plano, e por conseguinte irá aprender a calcular a distância entre dois pontos pertencentes a este plano. Essas noções geométricas serão importantes para o leitor compreender como utilizar essas ferramentas em representações gráficas de funções matemáticas bem como em representações de problemas físicos do nosso cotidiano, tais como o movimento retilíneo uniforme.
Em seguida, o leitor será introduzido a conceito de funções matemáticas e suas representações gráficas, onde ferramentas gráficas, discutidas previamente, serão utilizadas para representar funções matemáticas com o objetivo de familiarizar o leitor com a representação gráfica de funções.
Finalmente, com os conhecimentos previamente acumulados sobre funções e representações gráficas, e com a introdução dos conceitos de distância percorrida, deslocamento, velocidade média e aceleração média, o leitor passará a estudar o movimento retilíneo uniforme de corpos físicos.
Vale lembrar que, ao final de cada seção desta unidade o leitor terá uma atividade para ser respondida relacionada com o conteúdo apresentado.
O sistema de coordenadas são importantes para determinar a posição de um ponto no espaço em relação a um dado referencial. O caso mais simples de um sistema de coordenadas é identificar um ponto sobre uma linha real utilizando o eixo dos números reais.
Nesta construção, dado um ponto arbitrário O posicionado sobre a reta real, o qual constitui a origem do eixo coordenado, a posição de qualquer ponto P desta reta é definida por sua coordenada. A figura 1.1 mostra a reta coordenada, onde a distância ao ponto P pode ser positiva ou negativa dependendo de qual lado o ponto se encontra com relação a posição da origem - pontos localizados à esquerda do ponto de origem O são, por construção, considerados negativos, e a direita positivos. Outro aspecto importante desse sistema de coordenadas é o de que cada ponto na reta é identificado unicamente por uma coordenada.
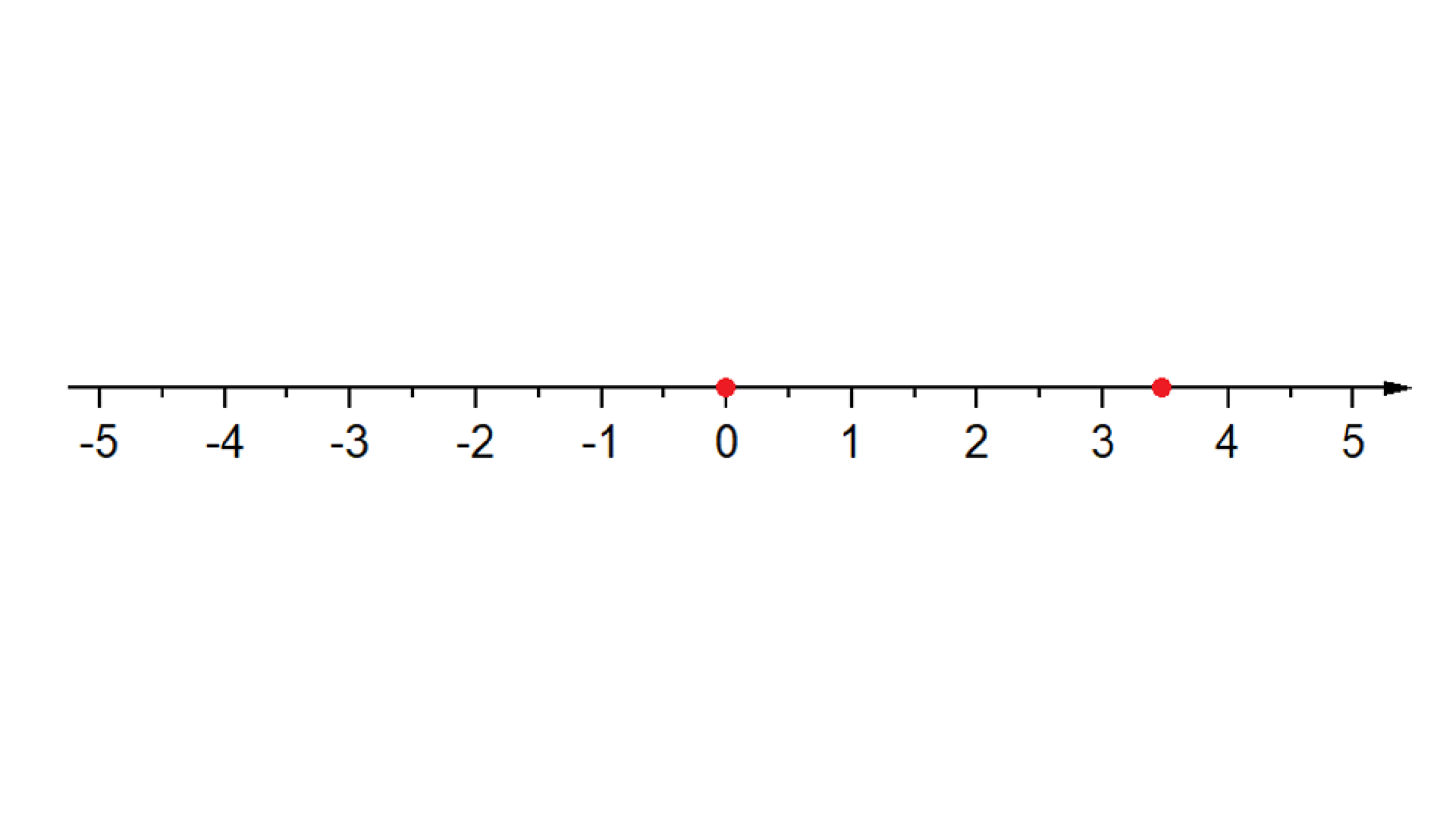
De forma análoga a reta coordenada em uma dimensão, para se determinar a posição de um ponto sobre uma superfície plana em duas dimensões, utiliza-se o plano cartesiano ortogonal. Esse sistema de coordenadas é definido por dois eixos coordenados ortogonais, como mostra a figura 1.2, os quais se cruzam no ponto de origem. Os dois eixos dividem o plano em quatro regiões denominadas quadrantes como mostrado na figura 1.2. Assim, uma vez estabelecido o sistema de coordenadas cartesianas, a posição de um ponto pertencente a este plano será definida por um único par de coordenadas \(\left( x,y \right)\), onde \(x\) pertence ao eixo da abscissa, e \(y\) ao eixo da ordenada.
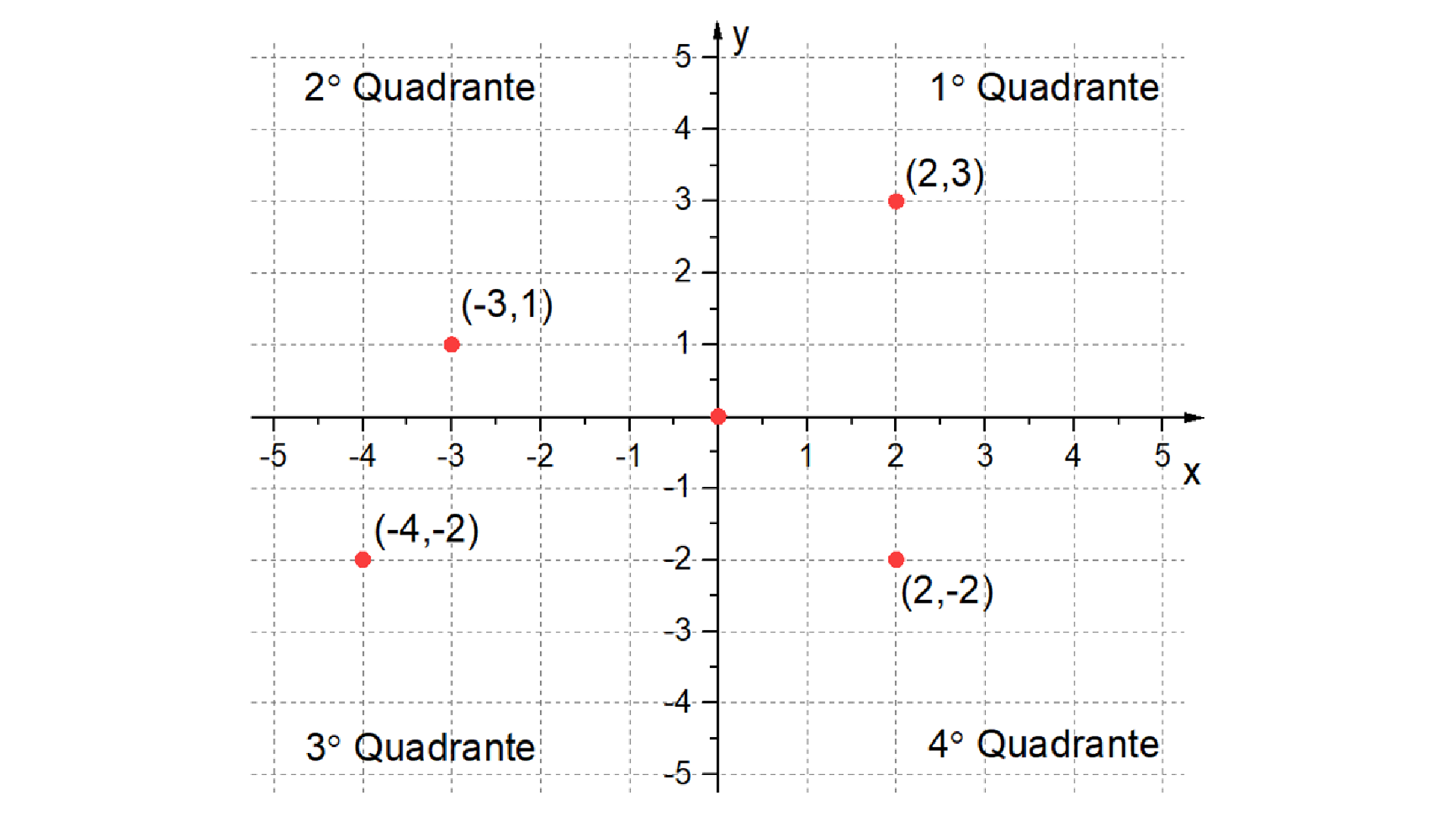
A figura mostra as coordenadas de 4 pontos no plano: (2,3), (-3,1), (-4,2) e (2,-2) localizados no \(1{}^\text{o}\), \(2{}^\text{o}\), \(3{}^\text{o}\) e \(4{}^\text{o}\)quadrante respectivamente.
Quando conhecemos as coordenadas de dois pontos A e B no plano cartesiano, é possível calcular a distância \(d\left( A,B \right)\) entre os dois pontos. Desse modo, sejam as coordenadas do ponto A dadas por (\(x1,y1\)) e B por \(\left( x2,y2 \right)\), a distância entre os pontos é dada pela hipotenusa do triângulo retângulo formado como mostra a figura 1.3, e pode ser calculada através do teorema de pitágoras da seguinte forma:
\(d\left( A,B \right)=\sqrt{{{\left( x2-x1 \right)}^{2}}+{{\left( y2-y1 \right)}^{2}}}\)
A distância entre os pontos \(d\left( A,B \right)\) é dado pelo valor da hipotenusa formado pelo triângulo retângulo no gráfico.
Além do plano cartesiano ortogonal, podemos representar um ponto sobre uma superfície de duas dimensões através das coordenadas polares. Ou seja, as coordenadas polares são um sistema de coordenadas bidimensional com coordenadas \(r\) e \(\theta \). Podemos relacionar as coordenadas cartesianas \(x\)e \(y\) com as coordenadas polares \(r\) e \(\theta ,\) com auxílio das funções trigonométricas seno e cosseno, através das fórmulas:
\(x=r~cos~\theta \) e \(y=r~~sen~\theta \).
Fonte: Elaborado pela autora.
Como ficará claro nas seções seguintes, sistemas de coordenadas como o plano cartesiano estão presentes em diversas aplicações em física e matemática, tornando se também um instrumento importantes para diversas aplicações em computação gráfica.
Imagine um espectador assistindo ao lançamento do ônibus espacial Discovery a uma distância de \(1200m\) da plataforma de lançamento. Supondo que o ônibus espacial se desloca verticalmente, e que após um certo tempo atinge a altitude \(x\) como mostra a figura abaixo:
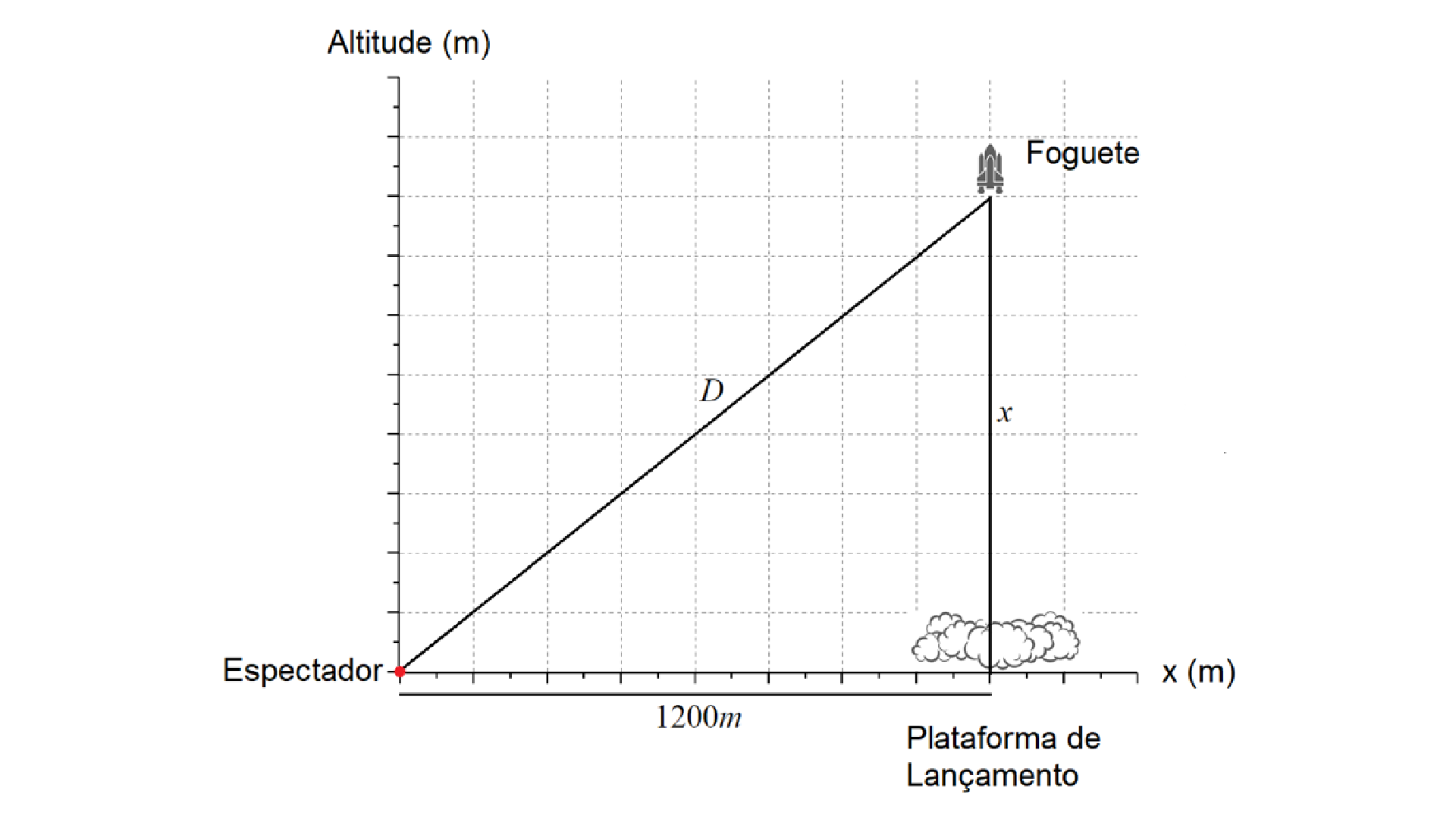
Qual será a distância entre o espectador e o ônibus espacial quando o foguete atingir a altitude de \(x=6000~m?\) Assinale a alternativa correta:
Muitas vezes, ocorre que o valor de uma quantidade depende do valor de outra quantidade. A relação entre tais quantidades é dada por uma função. Assim, uma variável \(y\) é uma função de outra variável \(x\), \(\left[ y=f\left( x \right) \right]\), se a cada valor do domínio de \(x\) corresponde a um único valor no conjunto da variável \(x\). Desse modo, considera-se que o número real \(y\) no conjunto \(Y\) como uma função do número real \(x\) no conjunto \(X\) se houver uma regra pela qual um valor específico de \(y\) seja atribuído a um valor de \(x\) como ilustra a figura 1.4.
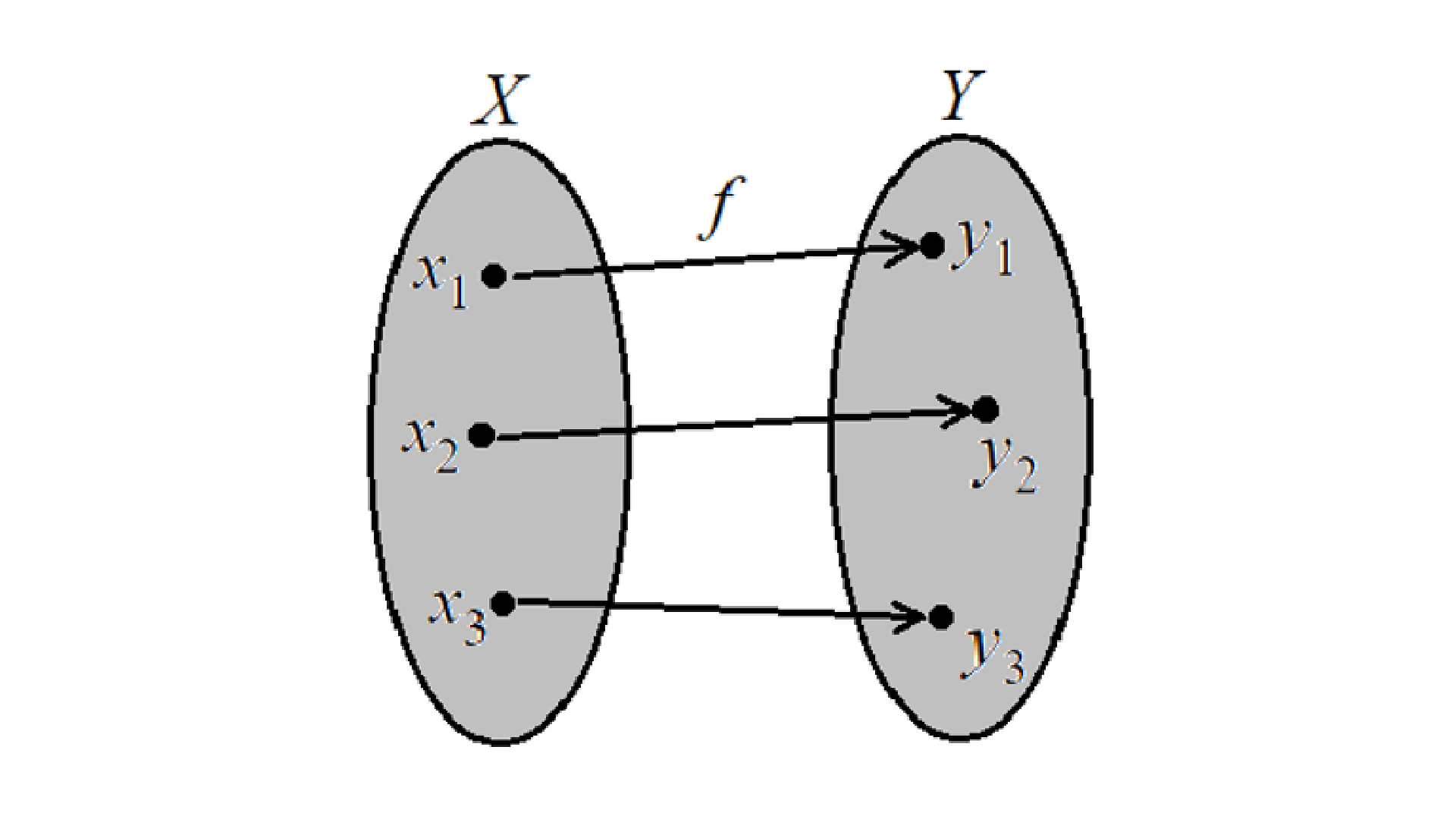
Definição: Uma função é um conjunto de pontos \(\left( x,y \right)\) onde ao se comparar quaisquer pares ordenados distintos de \(f\), nenhum terá o mesmo valor para o primeiro número \(x\). O conjunto dos valores de \(x\) é chamado de domínio da função, e o conjunto dos valores de \(y\) é chamado de imagem da função.
Essa definição assegura que \(y\) seja único para valores específicos de \(x\), o que garante que \(y\) seja uma função unívoca ou univalente de \(x\).
Os números \(x\) e \(y\) são variáveis, onde \(x\) é denominado variável independente e \(y\), a variável dependente a qual depende \(x\). O conceito de função como um conjunto de pares ordenado permite construir a seguinte definição para o gráfico de uma função.
Definição: Se \(f\) for uma função, então o gráfico de \(f\) será o conjunto dos pontos \(\left( x,y \right)\) no plano R2 para os quais \(\left( x,y \right)\) é um par ordenado de \(f\).
Lembre-se de que para uma função é preciso existir exatamente um valor da variável dependente para cada valor da variável independente. Em termos geométricos isso significa que ao se traçar uma reta vertical, o gráfico de uma função pode ser interceptado em no máximo um ponto. Observe que essa situação é verificada no gráfico da função na Fig. 1.5.
Observe que a linha vertical no gráfico intercepta o gráfico da função em um único ponto marcado em vermelho. Quando uma função é definida, o domínio da função deve ser dado explicitamente. Por exemplo se \(f\left( x \right)\) é uma função definida por:
\[f\left( x \right)~=~\frac{5x-2}{x+4}\]
isso implica que o conjunto \(x~\ne ~-4\), pois o quociente não está definido para \(x~=~-4\), logo o domínio de \(f\left( x \right)\) é o conjunto de todos os números reais exceto -4.
Subsequentemente, é possível definir operações com funções. Neste processo novas funções são formadas a partir de funções conhecidas através das quatro operações; soma, subtração, multiplicação e divisão.
Definição: Dadas duas funções \(f\left( x \right)\) e \(g\left( x \right)\):
(i)
a sua soma
,
denotada por f + g, é a função definida por
(f + g) (x) = f(x) + g(x)
(ii)
a sua soma
, denotada por f + g, é a função definida por
(f - g) (x) = f(x) - g(x)
(iii)
o seu produto
, denotada por f * g, é a função definida por
(f * g) (x) = f(x) * g(x)
(iv)
o seu quociente,
denotada por f / g, é a função definida por
(f / g) (x) = f (x) / g(x)
Para cada caso, o domínio da função resultante consiste nos valores de x comuns aos domínios de \(f\left( x \right)\) e \(g\left( x \right)\). Para o caso (iv) os valores de x onde \(g\left( x \right)=0\) são excluídos.
Outra operação importante consiste em obter a função composta de duas funções dadas. Essa operação é definida como:
Definição: Dadas duas funçõe s \(f\left( x \right)\) e \(g\left( x \right)\), a função composta denotada por \(f~\circ ~g\), é definida por
\[\left( f~\circ ~g \right)\left( x \right)=~f\left( g\left( x \right) \right)\]
onde o domínio de \(f~\circ ~g\) é o conjunto de todos os números x no domínio de \(g\) tal que \(g\left( x \right)\) esteja no domínio de \(f\) .
Como indica a definição, para calcular \(f~\circ ~g\), primeiro aplica-se a função \(g\) a \(x\) e em seguida a função \(f\) a \(g\left( x \right)\).
Um caça bombardeiro voa horizontalmente a \(A=500m\) de altitude, com uma velocidade constante de \(100m/s\), quando seu piloto recebe a ordem de seu radar para bombardear alvos que se encontram no nível do solo e a frente do avião como mostra a figura a seguir.
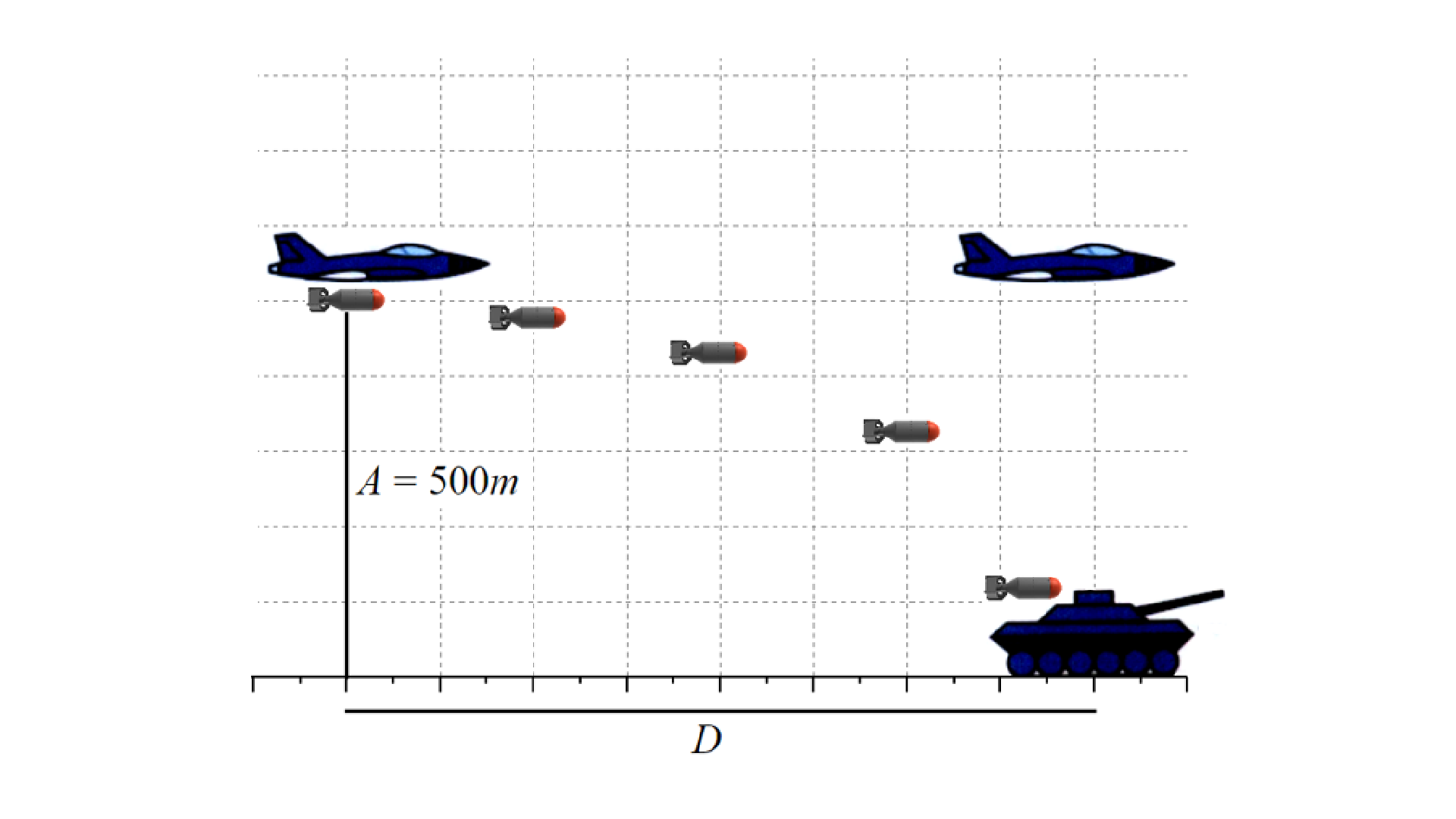
O piloto executa a ordem imediatamente atinge o alvo. Sabendo que dessa altitude a bomba leva \(10s\) para atingir o solo, e que a distância horizontal percorrida pela bomba obedece a função \(D\left( t \right)=vt~=~100t\), a qual está programada em seu radar, qual a distância horizontal \(D\), em metros, entre o avião e os alvos no instante que a bomba foi liberada?
A análise do movimento de um corpo físico é um problema fundamental em física. Das nossas experiências diárias, nos reconhecemos que o movimento é a mudança continua na posição de um objeto. Desse modo, se uma partícula está se movendo de uma posição inicial \({{x}_{0}}~\) para uma posição final \({{x}_{1}}\), é possível determinar a distância percorrida por um objeto através da diferença entre a posição final e a posição inicial na forma,
\[\Delta x={{x}_{1}}-~{{x}_{0}}\]
dessa definição, quando é atribuído os valores às posições \({{x}_{0}}\) e \({{x}_{1}}\), o deslocamento será positivo quando seu sentido for para a direita onde \({{x}_{1}}>{{x}_{0}}\), como ilustra a Fig. 1.8. Da mesma forma um deslocamento no sentido oposto, para a esquerda, onde \({{x}_{1}}<{{x}_{0}}\) resultará em um deslocamento negativo. Para exemplificar, imagine uma partícula que se move de \({{x}_{0}}=2m\) para =\({{x}_{1}}=10m\), seu deslocamento será \(\Delta x=10-2=+8m\), o resultado positivo indica que o deslocamento e no sentido positivo. Do mesmo modo, se a partícula se move de \({{x}_{0}}=15m\) para \({{x}_{1}}=-3m\), \(\Delta x=-3-15=-18m\), onde o resultado negativo indica que o movimento é para a esquerda.
Além da distância percorrida por um objeto, outra quantidade importante para o estudo do movimento é uma quantidade chamada deslocamento. Essa grandeza envolve apenas as posições inicial e final do objeto. Assim, por exemplo, imagine que um atleta de corrida que se move da posição \(x=10m\) para \(x=210m\) e , em seguida, volta para a posição \(x=10m\), o deslocamento desse atleta é \(D=10m-10m=0m\) mesmo tendo percorrido um percurso total de \(400m\).
Nesta seção, para simplificar a discussão, será considerado apenas o movimento em uma dimensão, como por exemplo o movimento de um automóvel em uma linha reta como ilustra a figura 1.6.
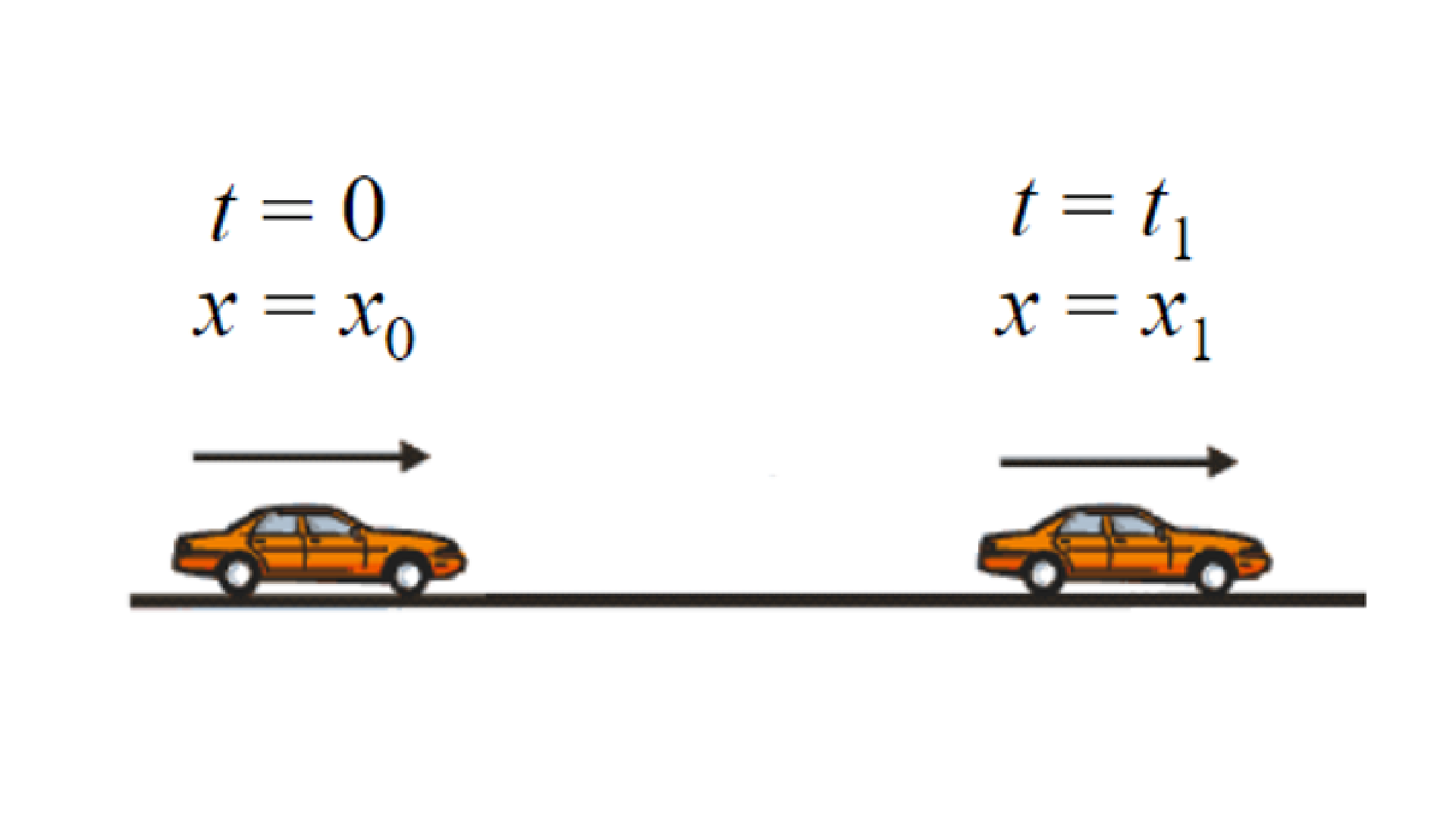
Para descrever o movimento é necessário adotar um referencial a partir do qual o movimento é descrito em relação a esse referencial. No caso do movimento unidimensional, o referencial é simplesmente uma reta orientada onde uma origem é escolhida. Neste referencial a posição de um corpo em movimento no instante \(t\) é descrita pelo valor da coordenada abscissa correspondente \(x\left( t \right)\).
De forma exemplificada, se considerarmos um carro em movimento em linha reta ao longo de uma estrada, \(x\left( t \right)\) é a posição ocupada pelo parachoque dianteiro do veículo no instante \(t\), é possível determinar a função \(x\left( t \right)\) através da medida da posição do automóvel em intervalos de tempo definidos \(\Delta t\). Pode-se assim obter o valor de x nos instantes \(0,~\Delta t,~2\Delta t,...\), de modo construir a tabela horária do movimento do tipo.
Da tabela horária é possível determinar a velocidade média do movimento que é definida por:
\[v~=~\frac{\Delta x}{\Delta t}~=~\frac{x\left( {{t}_{2}} \right)~-~x\left( {{t}_{1}} \right)}{{{t}_{2}}~-~~{{t}_{1}}}\]
ou seja, é a razão entre a distância percorrida \(\Delta x\) pelo veículo e o intervalo de tempo que o leva para essa distância percorrida ser produzida.
A velocidade média é medida em unidades de \(m/s\), no sistema internacional, ou \(km/h$\) conforme o problema em questão. Perceba que \(v\) pode ter valores positivos ou negativos. Avaliando a equação da velocidade média \(v~<~0\) quando \(\Delta x~<~0~\) ou seja quando o movimento se dá no sentido dos \(x\) decrescentes (o veículo está em marcha à ré).
Em seguida, para as situações onde a velocidade do automóvel varia aumentando ou diminuindo o seu valor durante um intervalo de tempo \(\Delta t\), esse movimento é tido como um movimento acelerado, e a aceleração média é definida como:
\[a=\frac{v\left( {{t}_{2}} \right)~-~v\left( {{t}_{1}} \right)}{{{t}_{2}}~-~{{t}_{1}}}=~\frac{\Delta v}{\Delta t}\]
essa fórmula indica que a aceleração é medida em unidades de \(m/{{s}^{2}}\) e mede a rapidez com que a velocidade varia em um dado intervalo de tempo.
Assim é comum dizer por exemplo que um veículo tem boa aceleração se ele é capaz de acelerar de \(0\) a \(30m/s\) em 3 segundos como ilustra a figura 1.7. Conforme esse experimento a aceleração média do veículo é de \(10m/{{s}^{2}}\), o que significa que a variação da velocidade do carro entre \(0\) e \(3s\) é de \(10m/s\) a cada 1 segundo.
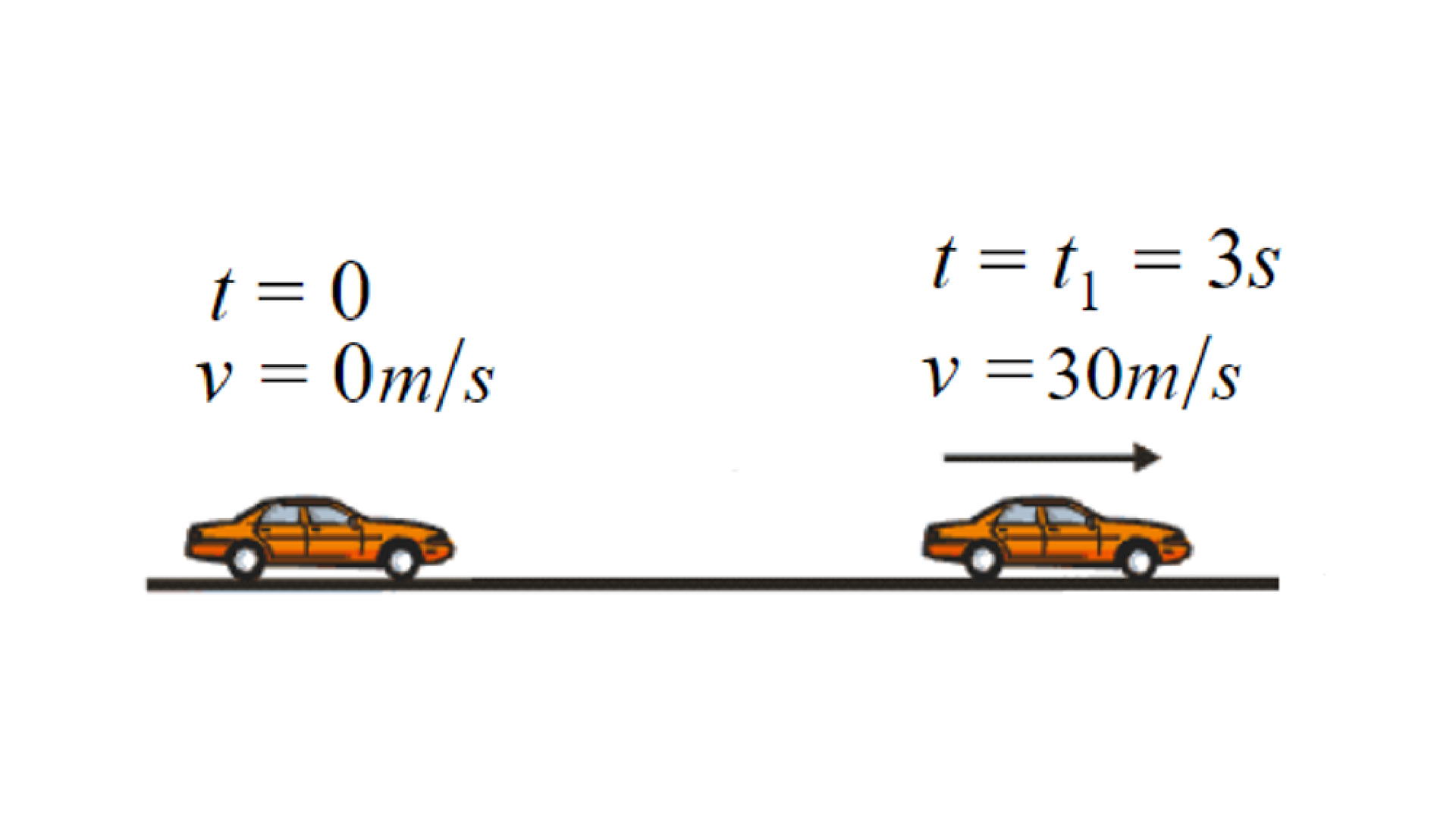
Através da equação da aceleração é possível observar que a aceleração é positiva quando a velocidade cresce no intervalo de tempo (carro acelerando), e negativa quando decresce (frenagem do carro).
Imagine um experimento onde um veiculo percorre uma trajetória retilínea e fotografias estroboscópicas, que permitem fotografar a posição do carro em intervalos de tempo iguais e constantes, são retiradas para o conjunto de três tipos de movimentos como ilustra os diagramas da figura a seguir:
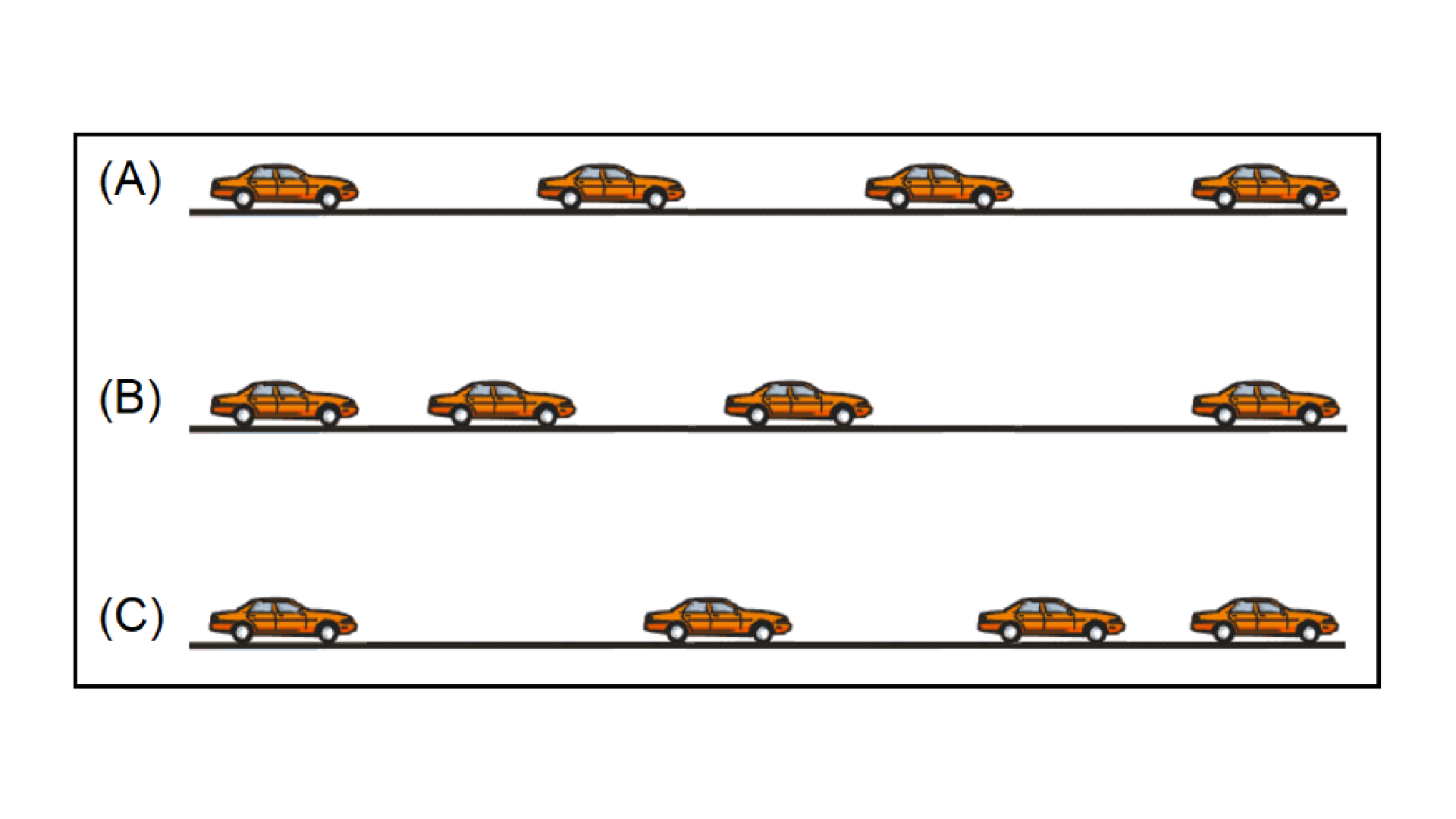
No diagrama A, as imagens do veículo estão igualmente espaçadas, mostrando que a distância percorrida pelo carro é a mesma para intervalos de tempos iguais. Neste caso a velocidade do veículo é constante?
No diagrama B, as imagens do veículo tornam-se mais distantes umas das outras com a progressão do tempo, mostrando que a cada intervalo de tempo adjacente o carro percorre uma distância maior. Neste caso a velocidade do veículo é constante? neste caso qual é o sinal da aceleração do veículo? o veículo está sendo acelerado ou desacelerado?
No diagrama C, a distância entre imagens adjacentes diminui com a progressão do tempo. Neste caso a velocidade do veículo está aumentando ou diminuindo? o veículo está sendo acelerado ou desacelerado?
Nosso objetivo neste tópico é estudar o movimento retilíneo uniforme. Para isto, primeiro vamos trabalhar com os conceitos sobre funções afins e suas propriedades.
A função afim, também denominada de função polinomial de 1º grau, é uma função \(f\) a qual é definida como:
Definição : É chamada função afim toda toda função polinomial de 1º grau na forma.
f) \[f\left( x \right)~=~ax+b\]
sendo \(a\) e \(b\) números reais .
Neste tipo de função, o número \(a\) é denominado coeficiente angular, e representa a inclinação da reta ou a taxa de crescimento ou variação da função. E \(b\) é chamado coeficiente linear e representa o ponto onde a reta intercepta o eixo \(y\) sendo também denominado por intercepto \(y\) da reta. A Fig. 1.8 trás graficamente a função de uma reta com o significado dos coeficiente \(a\) e \(b\).
O significado geométrico do coeficiente angular \(a\) e do coeficiente linear \(b\) são mostrado na figura. Agora será ilustrado alguns casos particulares da função afim com respeito aos valores adotados para as constantes \(a\) e \(b\).
Para o caso onde \(a\ne 0\) e \(b=0\) tem-se a chamada função linear. Seu gráfico intercepta a origem do plano cartesiano como ilustra a Fig. 1.9-A, onde temos o gráfico da função \(f\left( x \right)~=~2x\)
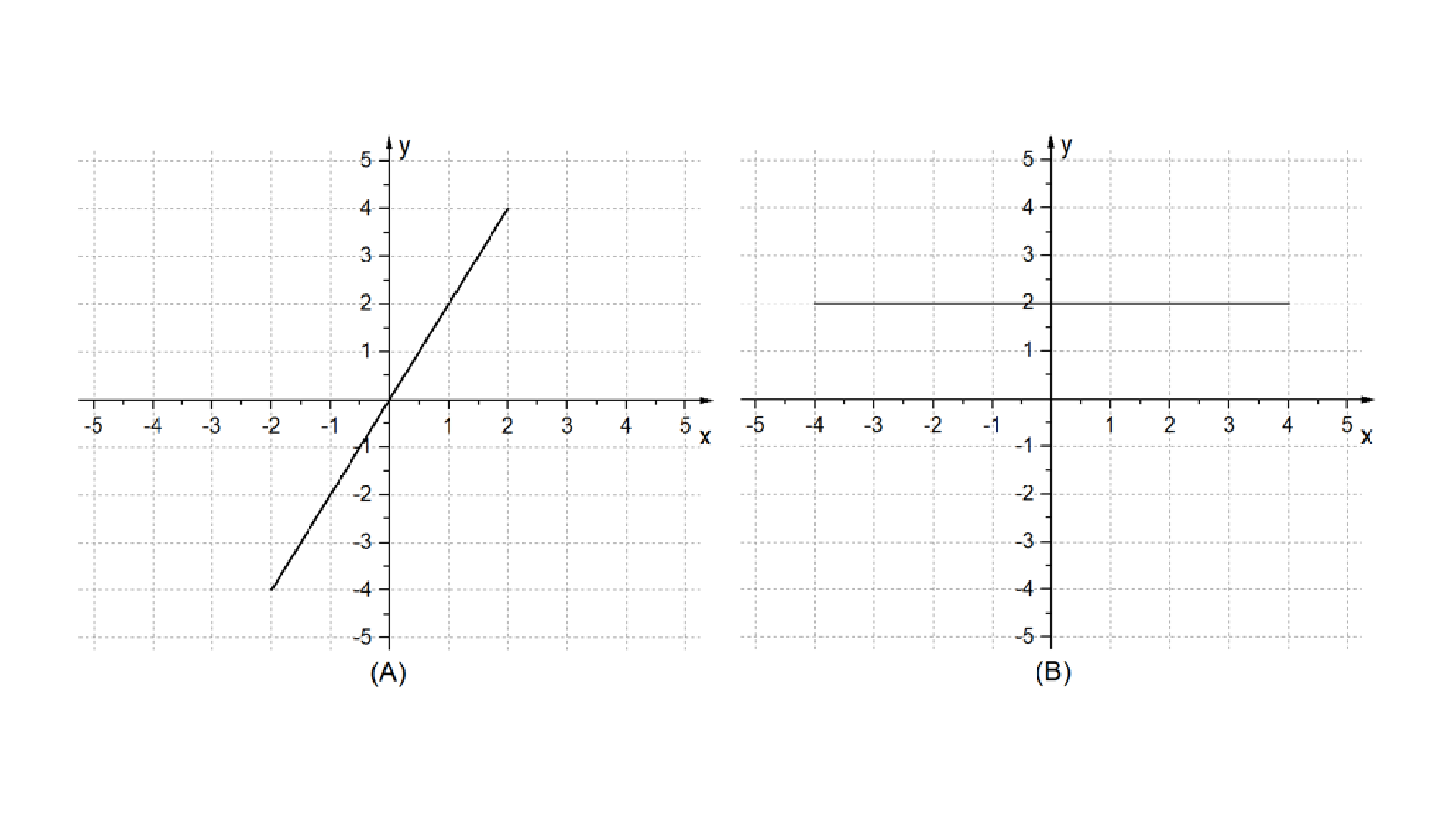
Para o caso onde \(a=0\) e \(b\ne 0\) tem-se a chamada função constante. Seu gráfico será sempre uma reta paralela ao eixo \(x\) e que intercepta o eixo \(y\) num ponto \(b\). A Fig. 1.9-B- mostra o gráfico da função \(f\left( x \right)~=~2\).
Observe o gráfico de uma função afim \(f\):
Sabemos que toda função afim é escrita na forma \(y=ax+b\). Então, através do gráfico ( Figura 1.10), podemos determinar os valores dos coeficientes \(a\) e \(b\) e a lei de formação da função \(f\).
Com efeito, conseguimos identificar os pontos \(\left( 2,0 \right)\) e \(\left( 0,2 \right)\) na Figura 1.10. Substituindo esses valores na fórmula geral \(f\left( x \right)=y\), temos:
Substituindo 2. em 1., obtemos \(a=~-1.\)
Logo, a lei de formação da função afim descrita graficamente pela Figura 1.13 é dada por \(f\left( x \right)=~-x+2\).
Como já podemos perceber durante nossos estudos até aqui, matemática e física são duas áreas de conhecimento que caminham lado a lado. Muitas fórmulas e conceitos matemáticos são utilizados para explicar fenômenos físicos. Por exemplo, o campo da física que estuda os movimentos dos corpos, denominado cinemática utiliza as funções afins para relacionar a posição de um movél com velocidade constante. Neste caso, o móvel possui aceleração?
Fonte: Elaborado pela autora.
O movimento mais simples é o movimento retilíneo uniforme onde a velocidade do corpo em movimento é constante. Esse movimento se caracteriza pelo fato de que percurso ou caminho percorrido iguais \(\Delta x~=~{{x}_{4}}~-{{x}_{3}}~=~{{x}_{2}}~-~{{x}_{1}}\) são descritos em intervalo de tempos iguais \(\Delta t~=~{{t}_{4}}~-{{t}_{3}}~=~{{t}_{2}}~-~{{t}_{1}}\). Isso implica que a função horária da posição é descrita por uma função afim na forma.
\[x\left( t \right)=at+b\]
onde como mostra a Figura 1.11, o coeficiente angular da reta \(a\) no gráfico \(x\left( t \right)\) versu \(t\) é idêntico a velocidade média \(v=~\Delta x/\Delta t\).
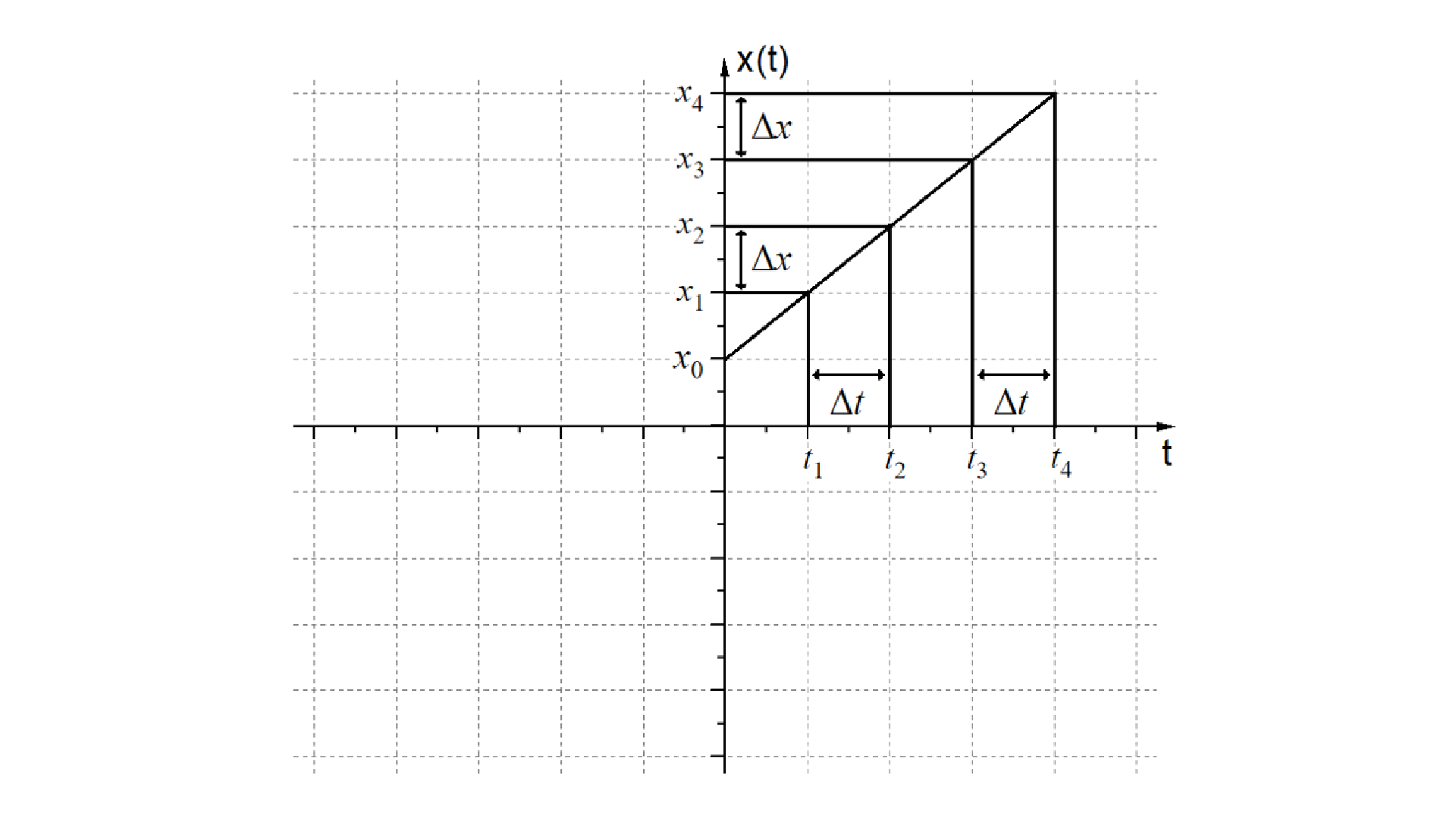
Em seguida considerando que no instante inicial do movimento, \({{t}_{0}}\), o veículo ocupa a posição \({{x}_{0}}\) chegaremos a conclusão que o coeficiente linear \(b={{x}_{0}}\) resultando na seguinte função horária para o movimento retilíneo uniforme.
\[x\left( t \right)={{x}_{0}}+v\left( t-{{t}_{0}} \right)\]
Com essa função é possível calcular a posição que veículo irá ocupar em instantes de tempo futuros, e desse modo determinar a sua trajetória.
Em uma tacada de um jogo de bilhar a bola branca é impulsionada com velocidade \(v\) em direção a bola amarela de acordo com a figura abaixo.
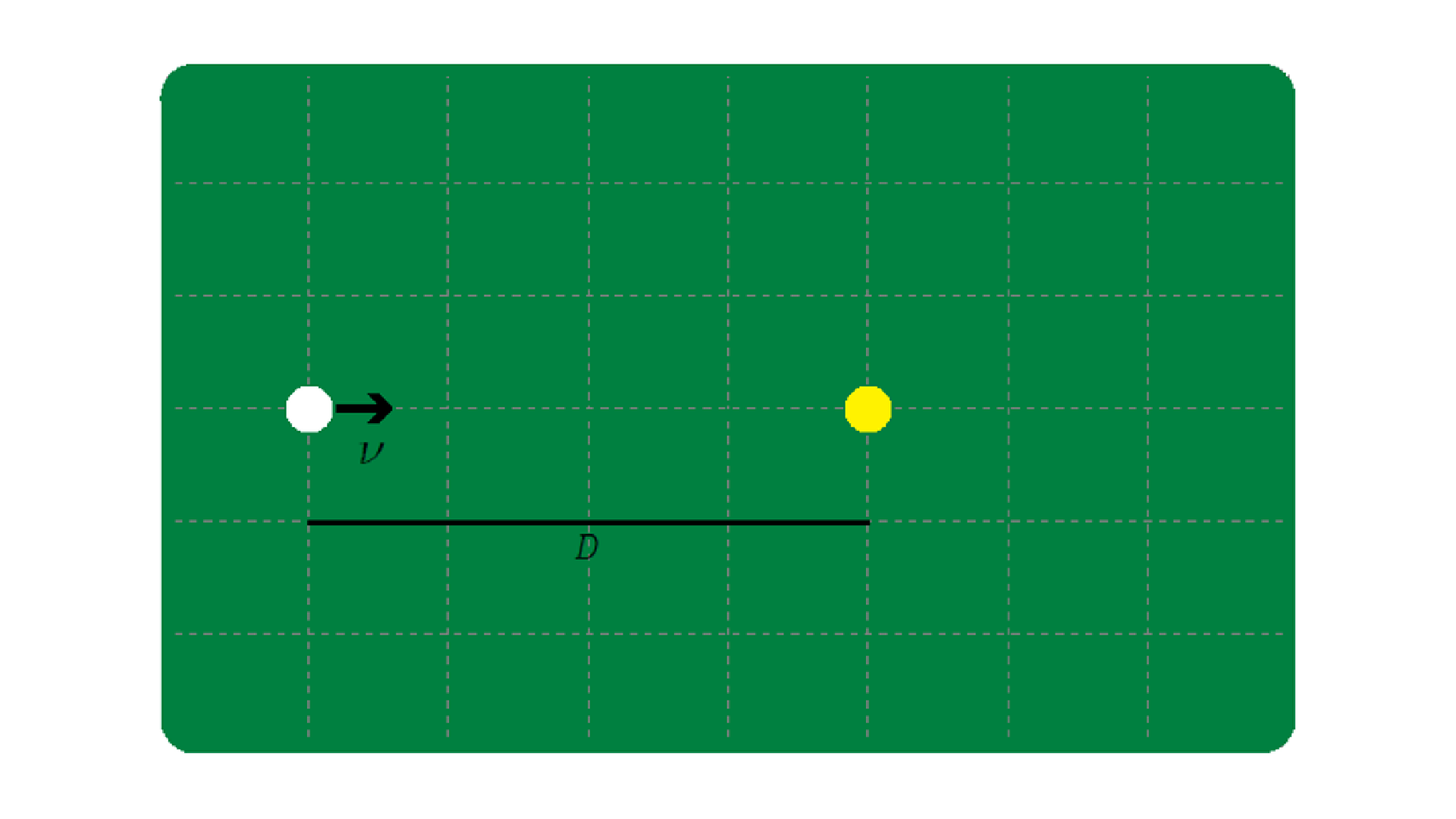
Assumindo que a bola branca se move com velocidade constante \(v=4m/s\), e que a distância entre as bolas é de \(D=12m\). O tempo que a bola branca leva até colidir com a bola amarela é de?

David Halliday, Robert Resnick e Jearl Walker
Editora: LTC-Livros Técnicos e Científicos Editora Ltda.
ISBN: 978-85-216-1903-l
Comentário: No capítulo II o leitor irá encontrar diversos exemplos relacionados com o estudo do movimento retilíneo uniforme.

Louis Leithold
Editora: Harbra.
ISBN: 85-294-0094-1
Comentário: Neste livro, no capítulo I o leitor encontrará maiores detalhes sobre o plano cartesiano e funções.
Tipo: Canal do YouTube
Comentário: Neste vídeo, o professor Marcelo Boaro discute o Movimento Uniformemente Variado, apresentando a equação da velocidade para este movimento.
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Tellus pellentesque eu tincidunt tortor aliquam nulla facilisi cras fermentum. Purus faucibus ornare suspendisse sed. Euismod quis viverra nibh cras pulvinar mattis nunc. At in tellus integer feugiat scelerisque. Porttitor lacus luctus accumsan tortor posuere. Nibh tortor id aliquet lectus proin nibh nisl condimentum.
CARVALHO, J. R. (Tradução). Coleção Schaum Cálculo diferencial integral: São Paulo: McGRAW-HILL do brasil Ltda. 1976.
HALLIDAY, D; RESNICK, R; WALKER, J. Fundamentos de Física, Volume 1, 9th edição: Rio de Janeiro: LTC-Livros Técnicos e Científicos Editora Ltda, 2012.
KAPLAN, W. Cálculo Avançado, Volume 1, 1st edição: São Paulo: Edgard Bluncher Ltda, 1972.
LEITHOLD, L. O Cálculo com Geometria Analitica Volume 1, 3th edição: São Paulo: Harbra, 1990.
NUSSENZVEIG, M. H. Curso de Física Básica Volume 1, 3th edição: São Paulo: Edgard Bluncher Ltda, 1997.