Ead.br

Equações e Funções Exponenciais

Na matemática, uma equação é uma igualdade entre duas expressões. Temos diversos tipos de equações, como, por exemplo, as equações do 2º grau, que são da forma $ax{}^\text{2}+bx+c=0,~a\ne 0$, onde x re presenta a incógnita, e a,b,c são constantes.

As equações exponenciais são outro tipo de equação, na qual a incógnita aparece no expoente. Por exemplo, ${{5}^{x}}=25$ é uma equação exponencial.

Geralmente, para solucionarmos uma equação exponencial, utilizamos propriedades de potenciação para igualar as bases das potências. Feito isso, usamos a propriedade

${{a}^{t}}={{a}^{x}}?t=x(a>0ea\ne 1)$

para obter o resultado.

saiba mais

Saiba mais

Para solucionarmos as equações exponenciais das mais diversas formas, precisamos conhecer e aplicar de forma correta as propriedades de potenciação aprendidas no ensino fundamental. Caso não se recorde dessas propriedades e/ou queira praticá-las, sugiro que faça uma revisão deste conteúdo. Em diversos sites, você encontra o conteúdo de potenciação com exemplos resolvidos e exemplos. Para saber mais, acesse o link a seguir.

ACESSAR

Observe os exemplos resolvidos a seguir:

${{2}^{x}}=32$

Note que $32={{2}^{5}}$, logo:

${{2}^{x}}={{2}^{5}}\Rightarrow x=5$.

${{3}^{x-2}}=81$

Como $81={{3}^{4}}$, temos:

${{3}^{x-2}}={{3}^{4}}\Rightarrow x-2=5\Rightarrow x=6$.

${{16}^{x}}=\frac{1}{{{4}^{x}}}$

Temos que:

${{16}^{x}}={{4}^{-x}}\Rightarrow \left( {{2}^{4}} \right){{~}^{x}}=\left( {{2}^{2}} \right){{~}^{-x}}\Rightarrow {{2}^{4x}}={{2}^{-2x}}\Rightarrow 4x=-2x\Rightarrow x=0~$

Também podemos resolver este exemplo da seguinte forma:

${{16}^{x}}={{4}^{-x}}\Rightarrow \left( {{4}^{2}} \right){{~}^{x}}=4{{~}^{-x}}\Rightarrow {{4}^{2x}}={{4}^{-x}}\Rightarrow 2x=-x\Rightarrow x=0~$.

${{\left( \frac{2}{5} \right)}^{3x}}=\frac{25}{4}$

De $\frac{25}{4}={{\left( \frac{5}{2} \right)}^{2}}={{\left( \frac{2}{5} \right)}^{-2}}$, obtemos

${{\left( \frac{2}{5} \right)}^{3x}}={{\left( \frac{2}{5} \right)}^{-2}}$

Donde, 3x=-2, ou seja, $x=-\frac{2}{3}$.

Também temos diversos tipos de funções. Quando a variável da função está no expoente, chamamos a função de função exponencial. Nesse caso, a base é maior que zero e diferente de um. Por exemplo, $h\left( x \right)~=~{{2}^{x}}$ e $g\left( x \right)=~{{\left( \frac{2}{5} \right)}^{x}}$ são funções exponenciais.

Sendo uma função exponencial qualquer dada por $f\left( x \right)~=~{{a}^{x}}$, temos que:

se a>1, f é uma função crescente. Logo, $h\left( x \right)~=~{{2}^{x}}$ é uma função exponencial crescente.

Graficamente temos:

Figura 3.1 - Função Exponencial Crescente
Fonte: Elaborada pela autora.

Se 0<a<1, f é uma função decrescente, logo, $g\left( x \right)=~{{\left( \frac{2}{5} \right)}^{x}}$ é uma função exponencial decrescente.

Graficamente:

Figura 3.2 - Função Exponencial Decrescente
Fonte: Elaborada pela autora.

Pelas Figuras 3.1 e 3.2, podemos observar que toda função exponencial passa pelo ponto (0,1), uma vez que todo número elevado a zero é 1. Também notamos que seu domínio é formado pelo conjunto dos números reais e que a imagem de qualquer função exponencial é sempre positiva.

Existem diversas aplicabilidades das funções exponenciais. Podemos utilizá-las no cálculo de juros compostos, para descrever a multiplicação de bactérias ou o decaimento radioativo, dentre outros.

Agora, vamos resolver um exemplo envolvendo função exponencial.

Suponha que um agricultor aplicou R$ 15 000,00 em uma cooperativa a uma taxa anual de 6,5% ao ano. Após 3 anos, qual será o montante a ser resgatado pelo agricultor?

Recordemos que a fórmula de juros compostos é dada por $M=C{{(1+i)}^{t}}$, onde C representa o capital, M representa o montante final, i taxa de juros em decimais e t o tempo de aplicação. Substituindo os dados, temos que:

$M=15~000~{{(1+0,065)}^{3}}=18~118,50$,

Ou seja, o agricultor terá um saldo de R$ 18 118,50 para resgatar.

praticar

Vamos Praticar

A função exponencial pode expressar um decrescimento ou crescimento presente em diversos experimentos na área da biologia, como na multiplicação de bactérias de uma cultura. Suponha que o número de bactérias de uma cultura pode ser previsto pela função f(t)=1200 $\times ~{{2}^{0,4~t}}$, onde o tempo está descrito em horas. Depois de quantas horas teremos 19 200 bactérias?

a) 2 horas. Feedback: alternativa incorreta , Pelos dados do enunciado, devemos determinar t que satisfaça a: N(t)=19 200, ou seja, $1200\times {{2}^{0,4~t}}=19~200$. Desta igualdade, temos que:
${{2}^{0,4t}}=\frac{19~200}{1~200}\Rightarrow {{2}^{0,4~t}}=16\Rightarrow {{2}^{0,4~t}}={{2}^{4}}\Rightarrow 0,4t=4\Rightarrow t=10$

b) 7 horas. Feedback: alternativa incorreta , Pelos dados do enunciado, devemos determinar t que satisfaça a: N(t)=19 200, ou seja, $1200\times {{2}^{0,4~t}}=19~200$. Desta igualdade, temos que:
${{2}^{0,4t}}=\frac{19~200}{1~200}\Rightarrow {{2}^{0,4~t}}=16\Rightarrow {{2}^{0,4~t}}={{2}^{4}}\Rightarrow 0,4t=4\Rightarrow t=10$

c) 8 horas. Feedback: alternativa incorreta , Pelos dados do enunciado, devemos determinar t que satisfaça a: N(t)=19 200, ou seja, $1200\times {{2}^{0,4~t}}=19~200$. Desta igualdade, temos que:
${{2}^{0,4t}}=\frac{19~200}{1~200}\Rightarrow {{2}^{0,4~t}}=16\Rightarrow {{2}^{0,4~t}}={{2}^{4}}\Rightarrow 0,4t=4\Rightarrow t=10$

d) 10 horas. Feedback: alternativa correta , Pelos dados do enunciado, devemos determinar t que satisfaça a: N(t)=19 200, ou seja, $1200\times {{2}^{0,4~t}}=19~200$. Desta igualdade, temos que:
${{2}^{0,4t}}=\frac{19~200}{1~200}\Rightarrow {{2}^{0,4~t}}=16\Rightarrow {{2}^{0,4~t}}={{2}^{4}}\Rightarrow 0,4t=4\Rightarrow t=10$

e) 15 horas. Feedback: alternativa incorreta , Pelos dados do enunciado, devemos determinar t que satisfaça a: N(t)=19 200, ou seja, $1200\times {{2}^{0,4~t}}=19~200$. Desta igualdade, temos que:
${{2}^{0,4t}}=\frac{19~200}{1~200}\Rightarrow {{2}^{0,4~t}}=16\Rightarrow {{2}^{0,4~t}}={{2}^{4}}\Rightarrow 0,4t=4\Rightarrow t=10$

Parabéns! Respostas enviadas. Aguarde.

Oops! Something went wrong while submitting the form.

Logaritmos e Funções Logarítmicas

Considere dois números reais positivos a e y, com a≠1. Denominamos logaritmo de y na base a o expoente x que satisfaz à igualdade ${{a}^{x}}=y$.

A notação utilizada para representar o logaritmo de y na base a é dada por $lo{{g}_{a}}~y$. Então, pelo que definimos anteriormente,

1. $lo{{g}_{a}}~y=x\Leftrightarrow {{a}^{x}}=y$.

Utilizando 1. para calcular $lo{{g}_{0,25}}~32$, temos que:

$lo{{g}_{0,25}}~32=x\Leftrightarrow {{(0,25)}^{x}}=32\Leftrightarrow {{\left( \frac{1}{4} \right)}^{x}}={{2}^{5}}\Leftrightarrow {{2}^{-2x}}={{2}^{5}}\Leftrightarrow -2x=5\Leftrightarrow x=-\frac{5}{2}$

ou seja, $lo{{g}_{0,25}}~32=-\frac{5}{2}$.

Podemos observar, na resolução deste exemplo, que, para determinar o logaritmo, precisamos resolver uma equação exponencial.

Usualmente, temos que log y representa o logaritmo de y na base 10.

Como consequência da definição, temos as seguintes propriedades:

i. $lo{{g}_{a}}~1=0$;

ii. $lo{{g}_{a}}~\left( ~x~.~y \right)=lo{{g}_{a}}~x~+~lo{{g}_{a}}~y$;

iii. $lo{{g}_{a}}~\left( \frac{x}{y} \right)=lo{{g}_{a}}~x-lo{{g}_{a}}~y$;

iv. $lo{{g}_{a}}~{{x}^{n}}=n~lo{{g}_{a}}~x$;

v. $lo{{g}_{~a}}~a=1$.

Estas propriedades podem ser úteis na resolução de exercícios. Por exemplo: considerando que log 2=0,3, log 3 = 0,45 e log 5 =0,6, vamos determinar log 7,5. Temos que:

$log~3,75~=~log\left( \frac{15}{4} \right)=log~15~-~log~4~=log~\left( 3.5 \right)-log~2{}^\text{2}=log~3~+log~5~-~2~logo~2=0,6$

Ainda supondo que log 2=0,3 e log 3 = 0,45, se desejarmos calcular $lo{{g}_{2}}~3$, devemos realizar a mudança de base. A mudança de base a para a base m de um logaritmo qualquer $lo{{g}_{a}}~y$ é dada por

$lo{{g}_{a}}~y=\frac{lo{{g}_{m~}}y}{lo{{g}_{m}}~a}$.

Então,

$lo{{g}_{2}}~3=\frac{log~3}{lo{{g}_{{}}}2}=\frac{0,45}{0,3}=1,5$.

Agora que sabemos trabalhar com os logaritmos, podemos definir a função logarítmica de base a como $f\left( x \right)~=~lo{{g}_{a}}~x$. Seguem diretamente da definição de logaritmo as seguintes propriedades:

a>0 e a≠1;
o domínio da função logarítmica é dado pelo conjunto dos números reais positivos.

As propriedades que acabamos de citar são conhecidas como condição de existência para uma função logarítmica, pois as usamos para determinar quais valores reais a função está definida.

Por exemplo, para determinar o domínio de $f\left( x \right)=lo{{g}_{x-1}}\left( 2x-x{}^\text{2} \right)$, devemos analisar quais valores de x satisfazem simultaneamente a

x-1>0; x-1≠1 e $x{}^\text{2}-1>0$,

Concluindo que o domínio de $f\left( x \right)=lo{{g}_{x-1}}\left( 2x-x{}^\text{2} \right)$ é formado pelo conjunto D(f)=[1,2[.

Assim como as funções exponenciais, se $f\left( x \right)=lo{{g}_{a~}}x$ é uma função logarítmica qualquer, temos que:

f é crescente se a>1.

Graficamente:

Figura 3.3 - Função logarítmica crescente
Fonte: Elaborada pela autora.

Por exemplo, $F\left( x \right)=lo{{g}_{2}}~x$ é uma função logarítmica crescente.

f é decrescente se 0<a<1.

Graficamente temos:

Figura 3.4 - Função Logarítmica Decrescente
Fonte: Elaborada pela autora.

Logo, $H\left( x \right)=~lo{{g}_{0,5}}~x$ é uma função logarítmica decrescente.

reflita

Reflita

Seja $f\left( x \right)=lo{{g}_{a~}}x$ uma função logarítmica e $g\left( x \right)={{a}^{x}}$ uma função exponencial. Utilizando as propriedades do logaritmo, temos que:

$f\left( g\left( x \right) \right)=f\left( ~{{a}^{x}} \right)=lo{{g}_{a~}}{{a}^{x}}=x~lo{{g}_{a}}~a=x$.

Com isso, podemos perceber que a função logarítmica é a inversa da função exponencial.

Também temos que a função exponencial é a inversa da função logarítmica. Então, quais propriedades de potenciação utilizamos para verificar que g(f(x))=x?

As aplicações da função logarítmica estão presentes em diversas áreas, como a matemática, física, química, biologia, entre outras.

praticar

Vamos Praticar

Uma empresa, contratou uma emissora de televisão para anunciar seu produto. O anúncio aparecerá diariamente no mesmo horário. Após t dias do início da exposição, estima-se que $y=3-9{{(0,5)}^{t}}$ milhões de pessoas terão conhecido o produto. Após quantos dias 1,2 milhões de pessoas conhecerão este produto? ( Utilize: log 2=0,2 e log 5 = 0,6)

a) 10 dias. Feedback: alternativa incorreta , Queremos encontrar t para y(t)=1,2, isto é, $3-9{{(0,5)}^{t}}=1,2$. Então:
$9{{(0,5)}^{t}}=1,8\Rightarrow {{0,5}^{t}}=0,2\Rightarrow log~{{0,5}^{t}}=log~0,2~\Rightarrow t~\left( log~5~-~log~10 \right)=log~2~-~log~10\Rightarrow 0,4~t=0,8$
⇒t=2.

b) 7 dias. Feedback: alternativa incorreta , Queremos encontrar t para y(t)=1,2, isto é, $3-9{{(0,5)}^{t}}=1,2$. Então:
$9{{(0,5)}^{t}}=1,8\Rightarrow {{0,5}^{t}}=0,2\Rightarrow log~{{0,5}^{t}}=log~0,2~\Rightarrow t~\left( log~5~-~log~10 \right)=log~2~-~log~10\Rightarrow 0,4~t=0,8$
⇒t=2.

c) 5 dias. Feedback: alternativa incorreta , Queremos encontrar t para y(t)=1,2, isto é, $3-9{{(0,5)}^{t}}=1,2$. Então:
$9{{(0,5)}^{t}}=1,8\Rightarrow {{0,5}^{t}}=0,2\Rightarrow log~{{0,5}^{t}}=log~0,2~\Rightarrow t~\left( log~5~-~log~10 \right)=log~2~-~log~10\Rightarrow 0,4~t=0,8$
⇒t=2.

d) 3 dias. Feedback: alternativa incorreta , Queremos encontrar t para y(t)=1,2, isto é, $3-9{{(0,5)}^{t}}=1,2$. Então:
$9{{(0,5)}^{t}}=1,8\Rightarrow {{0,5}^{t}}=0,2\Rightarrow log~{{0,5}^{t}}=log~0,2~\Rightarrow t~\left( log~5~-~log~10 \right)=log~2~-~log~10\Rightarrow 0,4~t=0,8$
⇒t=2.

e) 2 dias. Feedback: alternativa correta , Queremos encontrar t para y(t)=1,2, isto é, $3-9{{(0,5)}^{t}}=1,2$. Então:
$9{{(0,5)}^{t}}=1,8\Rightarrow {{0,5}^{t}}=0,2\Rightarrow log~{{0,5}^{t}}=log~0,2~\Rightarrow t~\left( log~5~-~log~10 \right)=log~2~-~log~10\Rightarrow 0,4~t=0,8$
⇒t=2.

Parabéns! Respostas enviadas. Aguarde.

Oops! Something went wrong while submitting the form.

Cálculo de Áreas, Volumes e Sistemas de Unidades

Quando vamos calcular a área ou o volume de uma superfície, precisamos verificar se as grandezas estão na mesma unidade de medida.

De acordo com o Sistema Internacional de Medidas (SI), a principal unidade de medida de comprimento é o metro (m). Depois, temos seus múltiplos que são o quilômetro (km), hectômetro (hm), decâmetro (dam) e seus submúltiplos decímetro (dm), centímetro (cm) e milímetro (mm).

A principal medida de capacidade, segundo o SI, é o litro (l). O litro também possui múltiplos, sendo eles o quilolitro (kl), hectolitro (hl), decalitro (dal) e submúltiplos dados por decilitro (dl), centilitro (cl) e mililitro (ml).

Como o sistema padrão de comprimento e capacidade é decimal, as transformações entre os múltiplos e submúltiplos são realizadas multiplicando ou dividindo por 10, como podemos observar nos Quadros a seguir:

	Múltiplos		Medida base		Submúltiplos
km	hm	dam	m	dm	cm	mm
1000m	100m	10m	1m	0,1 m	0,01 m	0,001m

Quadro 3.1 - Unidades de Medida de Comprimento
Fonte: Elaborado pela autora.

	Múltiplos		Medida base		Submúltiplos
kl	hl	dal	l	dl	cl	ml
1000 l	100 l	10 l	1 l	0,1 l	0,01 l	0,001 l

Quadro 3.2 - Unidades de Medida de Capacidade
Fonte: Elaborado pela autora.

Similarmente, nas medidas de comprimento, a principal medida de área é o metro quadrado, e a principal medida de volume é o metro cúbico. Os múltiplos e submúltiplos também seguem essa semelhança. As transformações entre os múltiplos e submúltiplos, por sua vez, são realizadas multiplicando ou dividindo por 100 para as unidades de áreas e por 1000 para as unidades de volume. Por exemplo, 5 $m{}^\text{2}$ equivale a 10 00 $cm{}^\text{2}$ e 8,132 $km{}^\text{3}$ é igual a 8 132 $hm{}^\text{3}$.

Como os líquidos preenchem a forma do recipiente que estão inseridos, as medidas de capacidade e volume possuem uma relação entre si, donde temos que 1 000 l = 1 $m{}^\text{3}$, ou equivalentemente, 1 l = 1 $dm{}^\text{3}$. Logo, se uma piscina possui volume igual a 10 $m{}^\text{3}$, sua capacidade é de 10 000 litros de água.

A área é a medida de uma superfície, logo trabalhamos com duas dimensões. Já o volume é a medida que um corpo ocupa no espaço. Então, para calcular o volume, consideramos três dimensões. Com isso, não conseguimos calcular o volume de uma figura plana, somente sua área. Entretanto, para as figuras do espaço conhecidas como sólidos geométricos, podemos determinar a área e o volume.

Recordemos as fórmulas para calcular a área de uma figura plana:

Figura 3.5 - Fórmulas para Área de Figuras Planas
Fonte: Elaborada pela autora.

A seguir, reunimos alguns sólidos geométricos com suas respectivas fórmulas:

Figura 3.6 - Fórmulas para Área e Volumes de Sólidos Geométricos
Fonte: Elaborada pela autora.

Agora, vamos resolver alguns exemplos:

Considere um cubo de área igual a 24 $m{}^\text{2}$. Qual é o volume desse cubo, em centímetros cúbicos?

Pela fórmula da área do cubo, temos que:

$6~l{}^\text{2}~=24\Rightarrow l=2~$

Logo, o lado desse cubo mede 2 metros. Substituindo este valor na fórmula do volume, obtemos:

$V=2{}^\text{3}=8~m{}^\text{3}$.

Porém, $8m{}^\text{3}~=~8~000~000~cm{}^\text{3}$. Assim, o volume do cubo é $8~000~cm{}^\text{3}$.

Esta não é a única forma de resolver este problema. Também poderíamos ter transformado a unidade de medida de comprimento do lado do cubo para centímetros antes de calcular o volume, ou seja, transformado 2 metros em centímetros. Como 2 m =200 cm, pela fórmula do volume, teríamos:

$V=\left( 200 \right){}^\text{3}=8~000~000~cm{}^\text{3}$,

Como anteriormente.

Observe a figura a seguir:

Figura 3.7 - Trapézio
Fonte: Elaborada pela autora.

Qual é a área do trapézio anterior?

Nesse caso, temos que a base maior do trapézio mede 0,6 hm. A base menor mede 15 dm, e a altura é igual a 3 m. Para calcular a área, precisamos trabalhar com a mesma unidade de medida. Então, antes do cálculo da área, precisamos transformar as medidas de comprimento para uma unidade em comum. Como o enunciado não especificou qual unidade de área a resposta precisa estar, podemos escolher uma. Temos que,

0,6 hm=6 m 15dm=1,5 m

Substituindo esses valores na fórmula da área, obtemos:

$A=\frac{\left( 6+1,5 \right)~3}{2}=11,25~m{}^\text{2}$.

Assim, este trapézio possui área igual a 11,25 metros quadrados.

praticar

Vamos Praticar

Um reservatório está sendo construído para estudantes realizarem experimentos. Suas dimensões são: 7 metros de comprimento, 4 metros de largura e 1,5 metros de profundidade. Os alunos precisam comprar uma substância líquida que ocupará um terço da capacidade deste reservatório. Quantos litros desta substância eles devem comprar?

a) 4 200 litros. Feedback: alternativa incorreta , Pela fórmula do volume, V = 7 . 4. 1,5 = 42 $m{}^\text{3}$. Porém, 1 $m{}^\text{3}$ = 1000 l, logo a capacidade do reservatório é de 42 000 litros. Como a substância ocupa um terço da capacidade do reservatório, e 42 000 dividido por 3 é 14 000, temos que os alunos precisam comprar 14 000 litros desta substância.

b) 14 000 litros. Feedback: alternativa correta , Pela fórmula do volume, V = 7 . 4. 1,5 = 42 $m{}^\text{3}$. Porém, 1 $m{}^\text{3}$ = 1000 l, logo a capacidade do reservatório é de 42 000 litros. Como a substância ocupa um terço da capacidade do reservatório, e 42 000 dividido por 3 é 14 000, temos que os alunos precisam comprar 14 000 litros desta substância.

c) 28 000 litros. Feedback: alternativa incorreta , Pela fórmula do volume, V = 7 . 4. 1,5 = 42 $m{}^\text{3}$. Porém, 1 $m{}^\text{3}$= 1000 l, logo a capacidade do reservatório é de 42 000 litros. Como a substância ocupa um terço da capacidade do reservatório, e 42 000 dividido por 3 é 14 000, temos que os alunos precisam comprar 14 000 litros desta substância.

d) 35 000 litros. Feedback: alternativa incorreta , Pela fórmula do volume, V = 7 . 4. 1,5 = 42 $m{}^\text{3}$. Porém, 1 $m{}^\text{3}$ = 1000 l, logo a capacidade do reservatório é de 42 000 litros. Como a substância ocupa um terço da capacidade do reservatório, e 42 000 dividido por 3 é 14 000, temos que os alunos precisam comprar 14 000 litros desta substância.

e) 42 000 litros. Feedback: alternativa incorreta , Pela fórmula do volume, V = 7 . 4. 1,5 = 42 $m{}^\text{3}$. Porém, 1 $m{}^\text{3}$ = 1000 l, logo a capacidade do reservatório é de 42 000 litros. Como a substância ocupa um terço da capacidade do reservatório, e 42 000 dividido por 3 é 14 000, temos que os alunos precisam comprar 14 000 litros desta substância.

Parabéns! Respostas enviadas. Aguarde.

Oops! Something went wrong while submitting the form.

Áreas e Volumes de Regiões Compostas

Como vimos no tópico anterior, as figuras planas de três ou quatro lados possuem fórmulas para determinar sua área. Porém, existem diversas figuras planas que não possuem fórmula, como a figura a seguir.

Figura 3.8 - Região Plana
Fonte: Elaborada pela autora.

Nesse caso, devemos decompor a região em regiões planas que sabemos como calcular a área, e, para determinar a área da região original, devemos calcular a áreas das regiões decompostas e somá-las. Observe a figura a seguir:

Figura 3.9 - Região Plana Decomposta
Fonte: Elaborada pela autora.

A Figura 3.9 mostra a decomposição da Figura 3.8 em duas figuras planas que temos fórmulas para calcular a área. A região I é um triângulo, e a região II é um trapézio. Considerando as medidas do triângulo e trapézio são, respectivamente b=h=3 cm e B=6cm,b=4cm e h=3cm, temos que a área da região I e II são, respectivamente:

${{A}_{I}}=\frac{3.3}{2}=4,5~cm{}^\text{2}$ e ${{A}_{II}}=\frac{\left( 6+4 \right)~3}{2}=15~cm{}^\text{2}$.

Entretanto, como a região da Figura 3.8 é a junção das regiões I e II, sua área é igual a:

$~A={{A}_{I}}+{{A}_{II}}=4,5~cm{}^\text{2}+15cm{}^\text{2}=19,5~cm{}^\text{2}$.

Vale ressaltar que, para realizar esta soma, precisamos prestar atenção se estamos trabalhando com a mesma unidade de medida. Caso não esteja, antes de somarmos, precisamos transformá-las.

Podemos utilizar o mesmo raciocínio para o cálculo do volume de regiões que não possuímos uma fórmula. Por exemplo, podemos decompor o sólido:

Figura 3.10 - Sólido Geométrico
Fonte: Elaborada pela autora.

Como dois paralelepípedos com medidas a=b=3 e c=1, e um paralelepípedo de medida a=b=1e c=3. Os volumes dos paralelepípedos são dados, respectivamente, por:

V=3.3.1=9 e V=1.1.3=3

Então, o volume do sólido geométrico da Figura 3.10 é igual a:

V= 9+9+3=21 unidades de volume.

praticar

Vamos Praticar

Uma praça da cidade de Marialva será revitalizada. Na Figura, podemos ver a região da praça que será cultivado um jardim.

Figura 3.11 - Região Da Praça
Fonte: Elaborada pela autora.

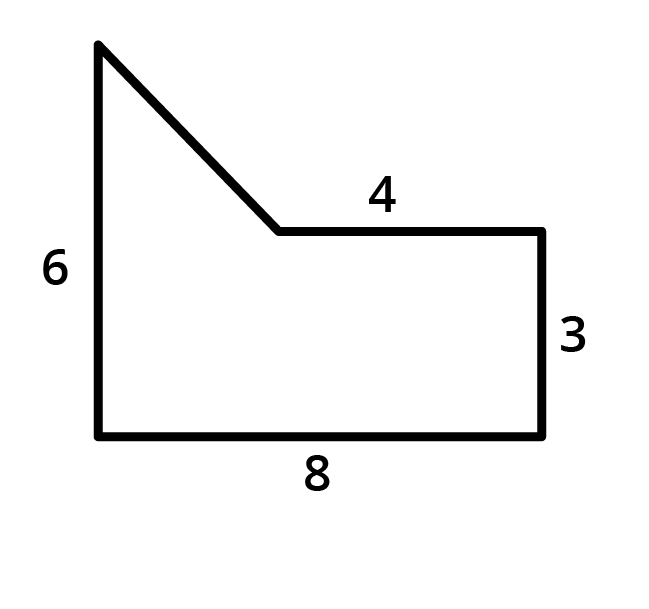
Considerando que as medidas anteriores estão em metros, qual será a área do jardim?

a) 30 metros quadrados. Feedback: alternativa correta , Podemos decompor a Figura em um triângulo de base, medindo 4 metros, e altura medindo 3 metros, e um retângulo com base medindo 8 metros, e altura medindo 3 metros. A área do triângulo é 6 $m{}^\text{2}$, e a área do retângulo é 24 $m{}^\text{2}$ . Logo, a área do jardim será de 6 + 24 = 30 metros quadrados.

b) 30 metros. Feedback: alternativa incorreta , Podemos decompor a Figura em um triângulo de base, medindo 4 metros, e altura medindo 3 metros, e um retângulo com base medindo 8 metros, e altura medindo 3 metros. A área do triângulo é 6 $m{}^\text{2}$, e a área do retângulo é 24 $m{}^\text{2}$. Logo, a área do jardim será de 6 + 24 = 30 metros quadrados.

c) 30 centímetros quadrados. Feedback: alternativa incorreta , Podemos decompor a Figura em um triângulo de base, medindo 4 metros, e altura medindo 3 metros, e um retângulo com base medindo 8 metros, e altura medindo 3 metros. A área do triângulo é 6 $m{}^\text{2}$, e a área do retângulo é 24 $m{}^\text{2}$. Logo, a área do jardim será de 6 + 24 = 30 metros quadrados.

d) 30 centímetros. Feedback: alternativa incorreta , Podemos decompor a Figura em um triângulo de base, medindo 4 metros, e altura medindo 3 metros, e um retângulo com base medindo 8 metros, e altura medindo 3 metros. A área do triângulo é 6 $m{}^\text{2}$, e a área do retângulo é 24 $m{}^\text{2}$. Logo, a área do jardim será de 6 + 24 = 30 metros quadrados.

e) 30 quilômetros. Feedback: alternativa incorreta , Podemos decompor a Figura em um triângulo de base, medindo 4 metros, e altura medindo 3 metros, e um retângulo com base medindo 8 metros, e altura medindo 3 metros. A área do triângulo é 6 $m{}^\text{2}$, e a área do retângulo é 24 $m{}^\text{2}$. Logo, a área do jardim será de 6 + 24 = 30 metros quadrados.

Parabéns! Respostas enviadas. Aguarde.

Oops! Something went wrong while submitting the form.

Cálculo

QUEBRANDO A BANCA