Começamos nossos estudos com as noções geométricas dos vetores. Considere um segmento orientado \(\left( A,B \right)\), ou seja, um par de pontos no espaço em que \(A\) é a origem do segmento e \(B\) a extremidade, como na figura a seguir:

O módulo ou norma de um segmento orientado é sua medida e é representado por \(\left| AB \right|.\) Note que os segmentos orientados \(\left( A,B \right)\) e \(\left( B,A \right)\) possuem o mesmo módulo, a mesma direção e sentidos opostos. Dois segmentos orientados são equivalentes se possuem a mesma direção, o mesmo sentido e o mesmo módulo. Chamamos de vetor determinado por um segmento orientado \(\left( A,B \right)\) a classe de equivalência de todos os segmentos orientados equivalentes a \(\left( A,B \right)\) e representamos por \(\underline{AB}\). Logo, qualquer segmento orientado \(\left( X,Y \right)\) equivalente a \(\left( A,B \right)\) é um representante do vetor \(\underline{AB}\).

Observações:

• Também podemos representar um vetor por letras minúsculas  encimadas por uma seta, por exemplo \(\vec{v},~\overrightarrow{a,}~\vec{b}\). Para simplificar a notação, quando não houver ambiguidade, denotaremos os vetores apenas por letras minúsculas \(v,~a,~b.\)
• Vamos representar o vetor nulo por \(\underset{\scriptscriptstyle-}{0}\). Ele é determinado pelo segmento nulo.
• Dado um vetor \(v=\underline{AB}~\), o vetor \(\underline{BA}~\) é o oposto de \(\underline{AB}~\) e é representado por \(-v=-\underline{AB}~\).
• Um vetor que possui norma igual a \(1\) é chamado de unitário.
• Dois vetores \(u~\)e \(v\) são paralelos se seus representantes são paralelos. Como o vetor nulo não possui direção, é paralelo a qualquer vetor. No próximo tópico veremos a representação algébrica dessa condição.

Como os vetores são elementos matemáticos, é natural nos perguntarmos se podemos realizar operações com eles. A resposta é: sim!

Considere o representante \(\left( A,B \right)\) do vetor \(u\) e o representante \(\left( B,C \right)\) do vetor \(v\).  Como a extremidade do vetor \(u\) coincide com a origem do vetor \(v\), a soma entre os vetores \(u\) e \(v\)é determinada pelo segmento orientado \(\left( A,C \right)\). Logo, o vetor soma tem a origem igual do primeiro vetor e extremidade igual ao segundo vetor. Geometricamente, o vetor \(u+v\) fecha o triângulo, como podemos observar na imagem a seguir.

A subtração entre \(u\) e \(v\) representados respectivamente por \(\left( A,B \right)\) e \(\left( A,C \right)\) é dada pela soma do vetor \(u\) com o oposto do vetor \(v\). Se construirmos o paralelogramo \(ABCD\), como na Figura 4.3, vemos que o vetor  \(u-v=u+\left( -v \right)=\underline{CB}.\)  Nesse caso, como ambos os vetores possuem a mesma origem, \(u+v=\underline{AD}.\)

Agora vamos considerar um vetor \(v\ne \underset{\scriptscriptstyle-}{0}\) e um número real \(k\) não nulo. A multiplicação de um vetor por um número real é um novo vetor \(u=~k.~v\), onde:

i) \(\left| u \right|=\left[ k \right].\left| v \right|\), onde \(\left[ k \right]\) representa o valor absoluto de \(k\);

ii) \(u\) possui a mesma direção de \(v\);

iii) \(u\) possui o mesmo sentido de \(v\) se \(k>0\) e u possui o sentido oposto de \(v\) se \(k<0.\)

A Figura 4.4 apresenta um exemplo da multiplicação de vetor por escalar.

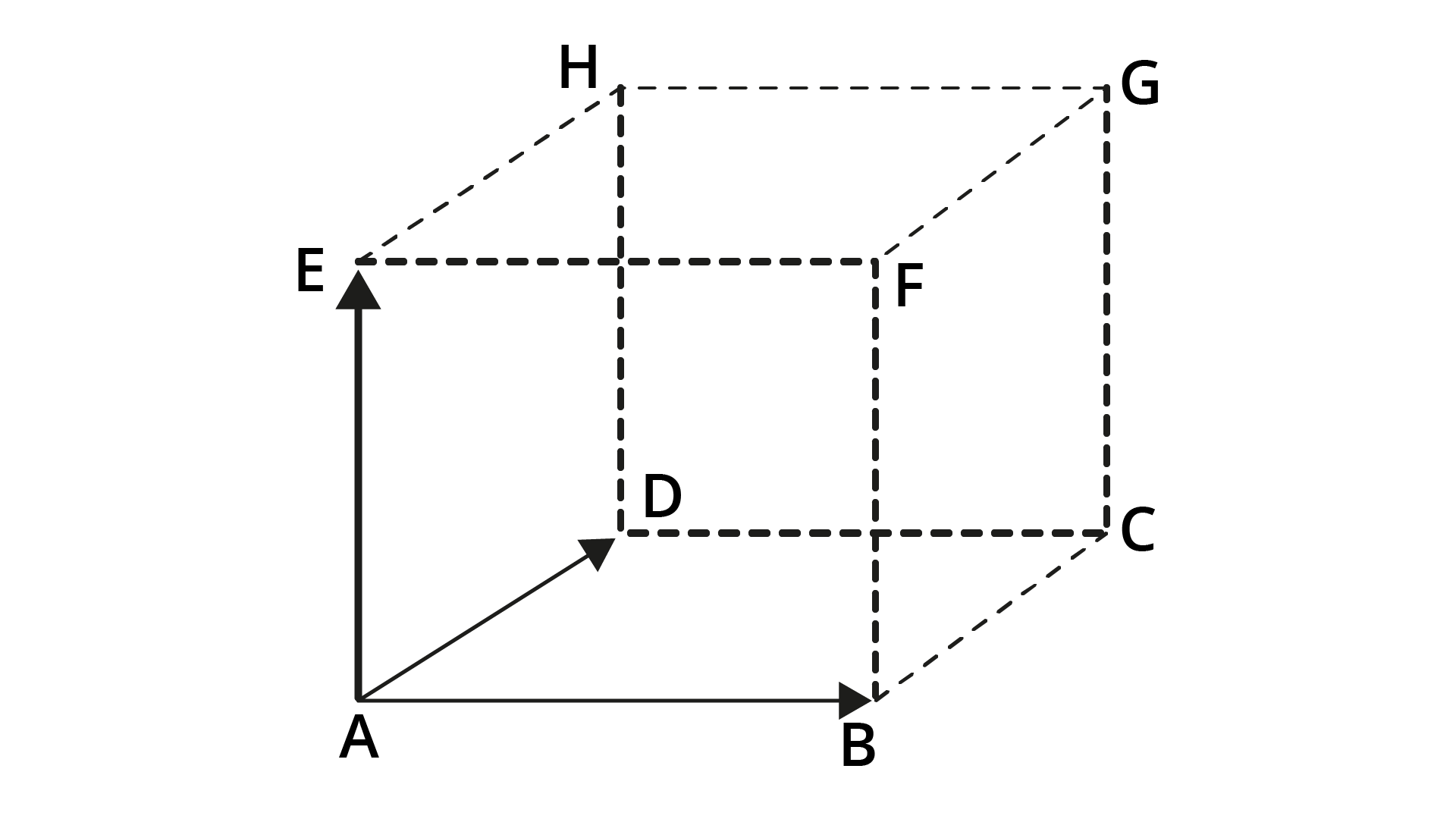
Neste tópico trataremos dos vetores na forma algébrica. Com isso, estaremos representando algebricamente fatos geométricos. Isso auxilia a aplicação do conceito de vetores em diversas áreas. Os conceitos apresentados para vetores no plano são estendidos para vetores no espaço.

A base ortonormal formada pelos vetores \(i=\left( 1,0 \right)\) e \(j=\left( 0,1 \right)\) determina o plano cartesiano. Então, dado qualquer vetor \(v\) no plano existe uma única dupla de números reais \(x\) e \(y\) satisfazendo: \(v=x~i~+~y~j\).

Nesse caso, também podemos representar o vetor \(v\) por: \(v=\left( x,y \right)\) e chamamos os números \(x\) e \(y\) de coordenadas do vetor \(v\).

Como as coordenadas são determinadas de maneira única, dois vetores \(u\) e \(v\) são iguais, se e somente se, suas coordenadas são iguais. Então, se \(u=\left( x+1,~2y-3 \right)\) e \(v=\left( -3,~11 \right)\) são iguais, para determinar os valores de \(x\) e \(y\), devemos igualar as coordenadas, ou seja,

\(x+1=~-3~\)     e      \(2y-3=11\)

Disso , obtemos:

\[x=~-4~ \text{e} ~y=7.~\]

O vetor nulo possui coordenadas iguais a \(\underset{\scriptscriptstyle-}{O}=\left( 0,0 \right)\).

Dados dois vetores \(u~=~\left( a,b \right)\) e \(v=\left( c,d \right)\) e \(k\) um número real, temos que:

• o oposto do vetor \(u\) é dado por:

\[-u=\left( -a,-b \right)\]

• a soma dos vetores \(u\) e \(v\) é dada por:

\[u+v=\left( a+c,~b+d \right);\]

• a subtração dos vetores \(u\) e \(v\) é dada por:

\[u-v=\left( a-c,~b-d \right);\]

• a multiplicação do vetor \(u\) e do número real \(k\) é dada por:

\[k~u~=\left( ka,~kb \right);\]

• a norma do vetor \(u\) é dada por:

\[\left| u \right|=\sqrt{a{}^\text{2}+b{}^\text{2}};\]

• os vetores \(u\) e \(v\) serão paralelos se existe \(c\in \Re \) tal que:

\[u=~c.~v\]

Dados os vetores \(u=\left( -3,2 \right)\) e \(v=\left( 4,-1 \right)\), vejamos alguns exemplos:

a) \(u+v=\left( -3,2 \right)+\left( 4,-1 \right)=\left( -3+4,~2+~\left( -1 \right) \right)=\left( 1,1 \right)\)

b) \(u-v=\left( -3,2 \right)-\left( 4,-1 \right)=\left( -3-4,~2-\left( -1 \right) \right)=\left( -7,3 \right);\)

c) \(2u~-~3v=2\left( -3,2 \right)-3\left( 4,-1 \right)=\left( 2.~\left( -3 \right),~2.~2 \right)-\left( 3.4,~3.\left( -1 \right) \right)=\left( -6,4 \right)-\left( 12,-3 \right)\) \(=~\left( -6-12,~4~-\left( -3 \right) \right)=\left( -18,~7 \right);\)

d) \(\left| -2v \right|=\left[ -2 \right]\left| v \right|=2\sqrt{4{}^\text{2}+\left( -1 \right){}^\text{2}}=2\sqrt{16+1}=2\sqrt{17};\)

e) O vetor \(w=\left( -9,~6 \right)\) é paralelo ao vetor \(u\), pois

\[w=\left( -9,6 \right)=3\left( -3,2 \right)=3.u,\]

Ou seja, existe um número real \(c=3\) tal que \(w=c.u\).

Também podemos definir as coordenadas de um vetor através da diferença de dois pontos. O vetor \(\underline{AB}~\)com origem em \(A\left( {{a}_{1}},{{a}_{2}} \right)\) e extremidade em \(B\left( {{b}_{1}},{{b}_{2}} \right)\) possui coordenadas dadas por \(x={{b}_{1}}-{{a}_{1}}\) e \(y={{b}_{2}}-{{a}_{2}}\), isto é,

\[\underline{AB}~=B-A=\left( {{b}_{1}}-{{a}_{1}},{{b}_{2}}-{{a}_{2}} \right).\]

Por exemplo, sendo \(A\left( -1,3 \right),~B=\left( 5,2 \right)\) temos que o vetor \(\underline{AB}=\left( 6,-1 \right)\), uma vez que:

\[\underline{AB}=\left( 5-\left( -1 \right),2-3 \right)=\left( 6,-1 \right).\]

Neste tópico, vamos tratar da multiplicação entre dois vetores. A primeira multiplicação que apresentaremos é o produto escalar de dois vetores. Como o nome indica, o resultado dessa operação é um escalar, um número. Depois, trabalharemos com o produto vetorial de dois vetores e, como veremos, o resultado do produto vetorial é um novo vetor. Por fim, estudaremos o produto misto entre vetores, que combina o produto escalar e o produto vetorial. No que segue, trabalharemos com vetores no espaço. Sejam \(u={{x}_{1}}i+{{y}_{1}}~j+{{z}_{1}}k=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\) e \(v={{x}_{2}}i+{{y}_{2}}~j+{{z}_{2}}k=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\), dois vetores.

O produto escalar entre \(u\) e \(v\) é representado por \(\left\langle u,v \right\rangle \) e é determinado por:

\[\left\langle u,v \right\rangle ={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}.\]

Por exemplo, se considerarmos os vetores \(u=\left( 2,~3,~1 \right)\) e \(v=\left( 3,~-1,~-1 \right)$\)temos que o produto escalar entre \(u\) e \(v\) é dado por:

\[\left\langle u,v \right\rangle =2.3+3.\left( -1 \right)+1.\left( -1 \right)=6-3-1=2.\]

O produto vetorial entre os vetores \(u\) e \(v\) é um vetor representado por \(u\times v\) com coordenadas \(x,~\left( -y \right)\) e \(z\), ou seja, \(u\times v=x~i+\left( -y \right)~j+z~k=\left( x,-y,z \right)\), onde coordenadas são determinadas por:

\[x=\det \left( \left| \begin{matrix}   {{y}_{1}} & {{z}_{1}}  \\   {{y}_{2}} & {{z}_{2}}  \\ \end{matrix} \right| \right)~;~~y=\det \left( \left| \begin{matrix}   {{x}_{1}} & {{z}_{1}}  \\   {{x}_{2}} & {{z}_{2}}  \\ \end{matrix} \right| \right)~;~~z=\det \left( \left| \begin{matrix}   {{x}_{1}} & {{y}_{1}}  \\   {{x}_{2}} & {{y}_{2}}  \\ \end{matrix} \right| \right)\]

Utilizando o cálculo de determinantes, concluímos que o produto vetorial entre dois vetores \(u={{x}_{1}}i+{{y}_{1}}~j+{{z}_{1}}k=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\) e \(v={{x}_{2}}i+{{y}_{2}}~j+{{z}_{3}}k=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\) pode ser determinado por:

\[u\times v=\left( {{y}_{1}}{{z}_{2}}-{{y}_{2}}{{z}_{1}} \right)~i~-\left( {{x}_{1}}{{z}_{2}}-{{x}_{2}}{{z}_{1}} \right)~j~+~\left( {{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}} \right)~k\]

\[~~~~~~~~=\left( {{y}_{1}}{{z}_{2}}-{{y}_{2}}{{z}_{1}},~-~\left( {{x}_{1}}{{z}_{2}}-{{x}_{2}}{{z}_{1}} \right),~{{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}} \right)~.\]

Então, sendo \(u=\left( 2,~3,~1 \right)\) e \(v=\left( -1,~0,~3 \right)\) temos que:

\[u\times v=\left( 3.3-0.1,~-~\left( 2.3-\left( -1 \right).1 \right),~2.0-\left( -1 \right).3~ \right)=\left( 9-0,~-\left( 6+1 \right),~0+3 \right)=\left( 9,-7,3 \right).\]

Geometricamente, o módulo do produto vetorial representa a área do paralelogramo determinado por \(u\) e \(v\). Esta é uma das aplicações dos vetores.

Exemplificando, se desejarmos calcular a área do paralelogramo formado pelos vetores \(u=\left( 3,1,2 \right)\) e \(v=\left( 4,-1,0 \right)\), devemos iniciar pelo cálculo do produto vetorial desses vetores: \(u\times v=\left( 0-\left( -2 \right),-\left( ~0-8 \right),~-3-4 \right)=\left( 2,8,-7 \right)\). Feito isso, precisamos determinar o módulo do vetor encontrado: \(\left| u\times v \right|=\sqrt{2{}^\text{2}+8{}^\text{2}+\left( -7 \right){}^\text{2}}=\sqrt{117}\). Então, a área do paralelogramo formado pelos vetores \(u\) e \(v\) é igual a \(\sqrt{117}~u.a.\)

Para finalizarmos este tópico, vamos falar sobre o produto misto. Além dos vetores \(u={{x}_{1}}i+{{y}_{1}}~j+{{z}_{1}}k=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\) e \(v={{x}_{2}}i+{{y}_{2}}~j+{{z}_{2}}k=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\) utilizados até aqui, vamos considerar o vetor \(w={{x}_{3}}i+{{y}_{3}}~j+{{z}_{3}}k=\left( {{x}_{3}},{{y}_{3}},{{z}_{3}} \right).\) O produto misto entre os vetores \(u\),\(v\) e \(w\) é igual ao produto escalar de \(u\) pelo vetor resultante do produto vetorial entre os vetores \(v\) e \(w\), ou seja,

\[\left\langle u,~v\times w \right\rangle \]

Logo, o resultado do produto misto é um número. Utilizando as fórmulas apresentadas para o cálculo do produto escalar e o produto vetorial, concluímos que:

\[\left\langle u,~v\times w \right\rangle ~= \det \left( \left| \begin{matrix}   {{x}_{1}} & {{y}_{1}} & {{z}_{1}}  \\   {{x}_{2}} & {{y}_{2}} & {{z}_{2}}  \\   {{x}_{3}} & {{y}_{3}} & {{z}_{3}}  \\ \end{matrix} \right| \right)={{x}_{1}}\left( {{y}_{2}}{{z}_{3}}-{{y}_{3}}{{z}_{2}} \right)-{{y}_{1}}\left( {{x}_{2}}{{z}_{3}}-{{x}_{3}}{{z}_{2}} \right)+{{z}_{1}}\left( {{x}_{2}}{{y}_{3}}-{{x}_{3}}{{y}_{2}} \right).\]

Então, sendo \(u=2i+3j+5k\), \(v=~-i+3j+3k\) e \(w=4i-3j+2k\) temos que o produto misto dos vetores \(u\),\(v\) e \(w\) é dado por:

\[\left\langle u,~v\times w \right\rangle ~=2\left( 3.2-\left( -3 \right).3 \right)-3\left( -1.2-4.3 \right)+5\left( -1.\left( -3 \right)-4.3 \right)\]

\[=2\left( 6+9 \right)-3\left( -2-12 \right)+5\left( 3-12 \right)=2.15-3.\left( -14 \right)+5.\left( -9 \right)=27\]

Seja \(A,~B,~C\) e \(D\) pontos que não estão num mesmo plano e considere o tetraedro formado por eles.

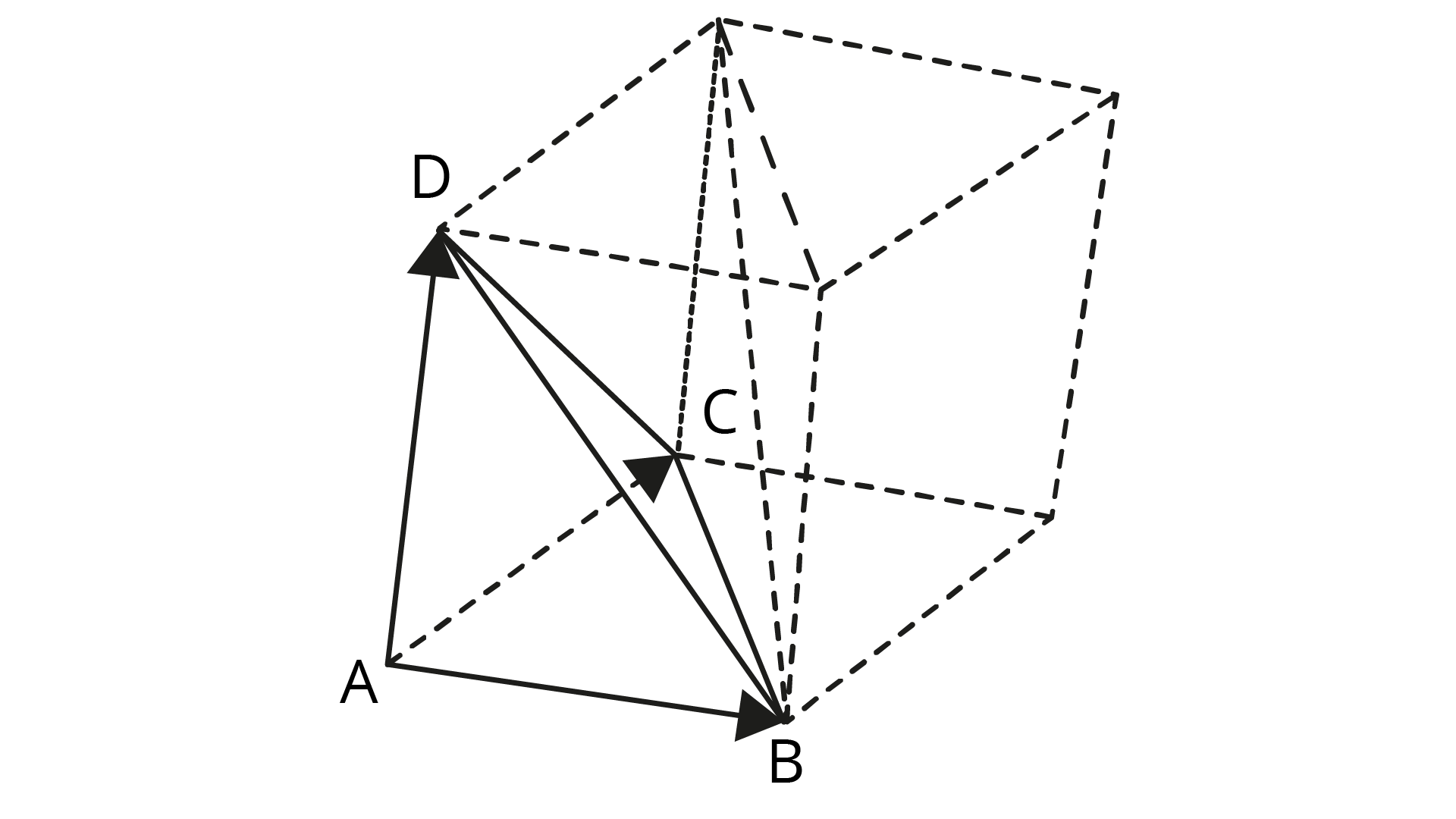
O valor absoluto do produto misto entre os vetores \(\underline{AB},~\underline{AC}\) e \(\underline{AD}~\)é igual ao volume do paralelepípedo formado por eles. Essa é a interpretação geométrica para o produto misto e outra aplicação dos vetores.

Como já pudemos perceber, os vetores estão presentes na Física quando precisamos representar grandezas que possuem módulo, direção e sentido como por exemplo o deslocamento, a velocidade, a aceleração, a força, dentre outras.

Na Física, podemos utilizar o produto escalar para determinar o trabalho realizado por uma força no decorrer de um deslocamento.

O produto vetorial também possui aplicações na Física, como obter o torque. O torque é um vetor e significa a possibilidade de um corpo alterar seu movimento de rotação ou de sofrer uma torção. Um exemplo cotidiano de torque é quando abrimos uma porta ou quando usamos uma chave de fenda.

Esse vetor pode ser determinado pelo produto vetorial entre os vetores força e distância, ou seja,

\[\tau =r~x~F\]

Onde \(\tau \) representa o torque, \(\left| r \right|\) a distância do ponto de aplicação da força ao eixo e \(F\) denota a força.

Se o produto vetorial dos vetores força e distância for nulo, dizemos que o corpo se encontra em equilíbrio rotacional. Pelo Sistema Internacional de medidas, a unidade do torque é o Newton vezes metro, representada por \(N.m\).

Por exemplo, considere uma com origem em A e extremidade em B, onde o vetor \(\underline{AB}=2j\), com unidade de medida em metros e uma força \(F=10~i\), com unidade de medida em Newtons. Sendo \(Oz\) o eixo de rotação, qual o valor do torque sobre a barra?

Pelo que mencionamos anteriormente,

\[\tau =r~x~F=\left( 0,2,0 \right)\times \left( 10,0,0 \right)=\left( 2.0-0.0,-\left( 0.0-10.0 \right),0.0-10.2 \right)=\left( 0,0,-20 \right)~N.m\]

ou, equivalentemente

\[\tau =-20~k~N.m.\]