QUÍMICA GERAL E
CIÊNCIA DOS MATERIAIS
Estrutura e propriedades dos sólidos
Os materiais que se encontram em estado sólido estão com seus átomos, íons ou moléculas distribuídos de tal maneira que garantem estabilidade entre si, propiciando essa estado da matéria. Grande quantidade dos materiais que são utilizados na engenharia no dia a dia, em especial o metal (existe uma gigantesca quantidade de diferentes tipos de metais), possui um arranjo geométrico muito bem definido entre os seus átomos, constituindo o que chamamos de estrutura cristalina. Um material é chamado de cristalino quando possui um agrupamento de átomos, íons ou moléculas que se repete nas três dimensões, independentemente do tipo de ligação.
O tipo de ligação química, a distribuição espacial dos átomos e o elemento químico em si estão fortemente correlacionados com as propriedades do material. Por menor que seja a alteração em qualquer um desses três fatores, há uma grande mudança nas propriedades. Neste capítulo, são abordados os assuntos que servem de suporte teórico para compreender a relação citada.
Os materiais sólidos são classificados em função da regularidade com que os átomos ou íons estão organizados entre si. Dizemos que um material é cristalino quando essa organização se repete ou possui periodicidade em grandes distâncias atômicas, ou seja, não basta que algumas dezenas de átomos organizados de maneira tridimensional estejam se repetindo, é necessário que esse padrão de organização se repita para alguns milhares de átomos.
É necessário ter em mente a importância de se conhecer a estrutura dos sólidos cristalinos, uma vez que as propriedades dos materiais estão intimamente ligadas à sua estrutura cristalina. Dependendo da estrutura cristalina, determinado material pode se apresentar como frágil, a exemplo do magnésio e do berílio, ou como dúctil, a exemplo do ouro e do cobre. Segundo Callister Junior e Rethwisch (2008), há diferenças significativas entre as propriedades dos materiais cristalinos e não cristalinos, mesmo sob composições idênticas.
Os átomos, no estado sólido, podem assumir diversos arranjos, a partir dos quais é possível compreender os conceitos de cristalinidade e não cristalinidade. O conceito de cristalinidade está diretamente relacionado à regularidade dos arranjos entre os átomos ou, mais precisamente, ao seu posicionamento. Ao longo de uma cadeia, os átomos alinham-se periódica ou repetitivamente, estabelecendo uma espécie de ordem . Quando esse alinhamento se estende e ocorre a solidificação, eles adotaram um padrão tridimensional. Os metais, alguns polímeros e alguns dos materiais cerâmicos possuem essa característica e, quando solidificados, formam o que se chama de estrutura cristalina.

A estrutura cristalina nada mais é do que a maneira como esses átomos estão organizados no espaço, sob diferentes formas e graus de complexidade (Figura 2.1).
A partir da definição de cristalinidade, verifica-se que existe uma ordem entre os átomos presentes nos sólidos cristalinos e que formam um padrão ao longo das estruturas. Ao dividir essas grandes estruturas em pequenas partes e considerar as unidades que se repetem, temos as menores frações cristalinas, que são denominadas células unitárias. Na maioria das estruturas cristalinas, as células unitárias possuem o formato de um paralelepípedo ou de um prisma, com três conjuntos de faces paralelas, conforme mostrado na Figura 2.2 (CALLISTER JUNIOR; RETHWISCH, 2008).
A célula unitária é a unidade básica de formação da estrutura cristalina que representa sua simetria, demonstrando todas as posições dos átomos do cristal por meio de translações integrais dos comprimentos ao longo de cada uma das arestas, definindo toda estrutura pela geometria e posição desses átomos. É importante salientar que se convencionou afirmar a coincidência entre os centros dos átomos e os vértices do paralelepípedo como representação de uma esfera rígida e a adoção de apenas uma única célula unitária para uma estrutura cristalina, apesar da possibilidade de termos mais de uma célula representando uma mesma estrutura.
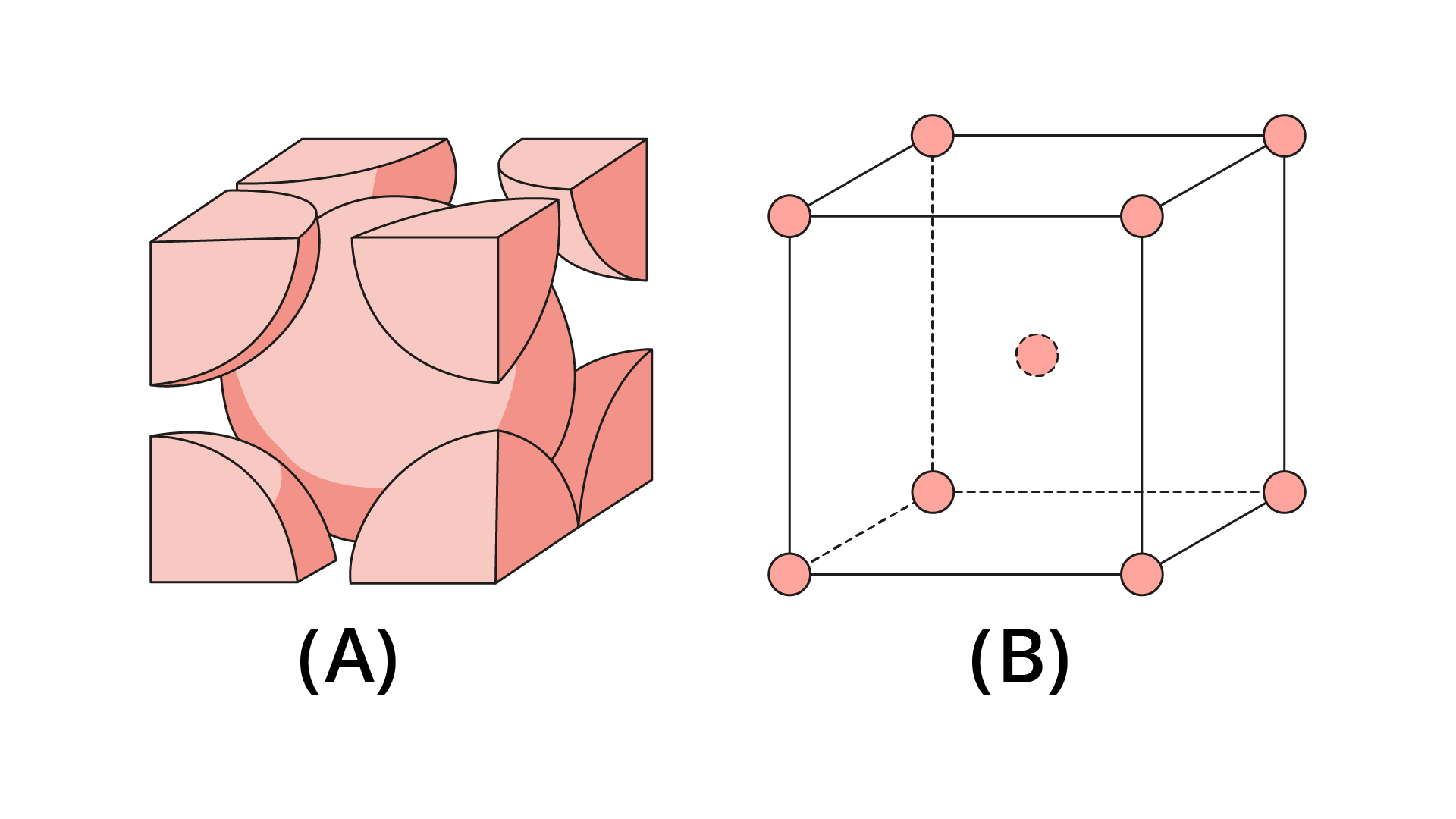
Existe uma quantidade bastante elevada de estruturas cristalinas diferentes, desde as mais simples, como as dos metais, até as mais complexas, como os polímeros e as cerâmicas. Entre as todas estruturas existentes, destaca-se a estrutura cúbica de faces centradas (CFC).
A estrutura CFC é caracterizada por possuir um átomo centralizado em cada uma das faces, conforme mostrado na Figura 2.3.
Em todas as estruturas, existem características que precisam ser analisadas. Entre elas, destacam-se o número de átomos dentro da célula unitária, o parâmetro de rede, o número de coordenação e o fator de empacotamento atômico.
Inicialmente, é necessário definir o comprimento da aresta (a), o raio atômico (R) que é uma grandeza geométrica tabelada para todos os átomos, e a relação geométrica entre esses dois. Na Figura 2.4, está demonstrada uma estrutura do tipo CFC com a respectiva relação entre “a” e “R”, denominada parâmetro de rede (CALLISTER JUNIOR; RETHWISCH, 2008).
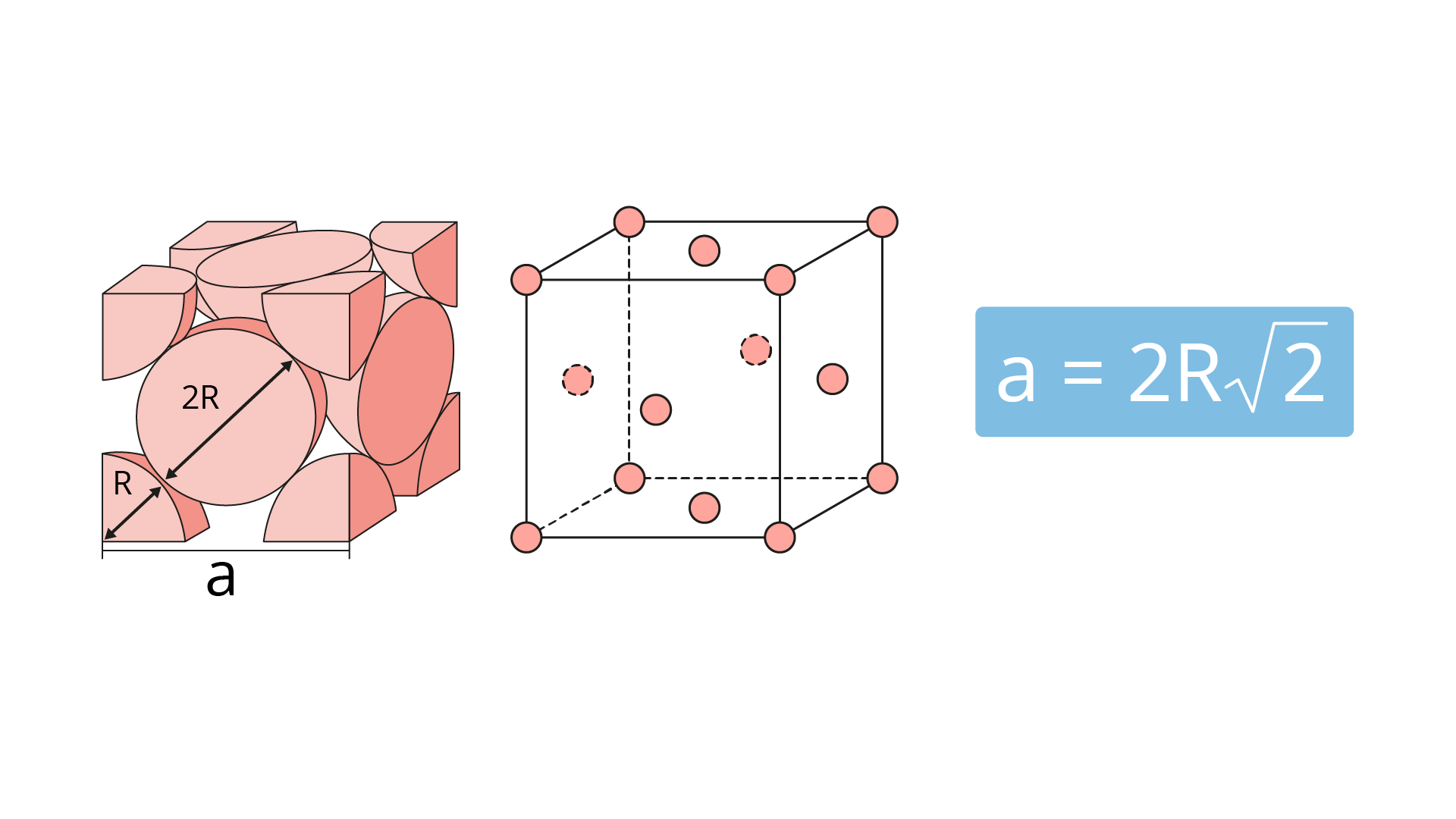
Em seguida, determina-se a quantidade de átomos dentro da célula unitária, utilizando o modelo das esferas rígidas.
Logo, em uma estrutura cristalina do tipo CFC, teremos o total de quatro átomos inteiros dentro da célula unitária.
Esta estrutura é caracterizada por possuir um átomo na parte central da célula unitária (Figura 2.5).
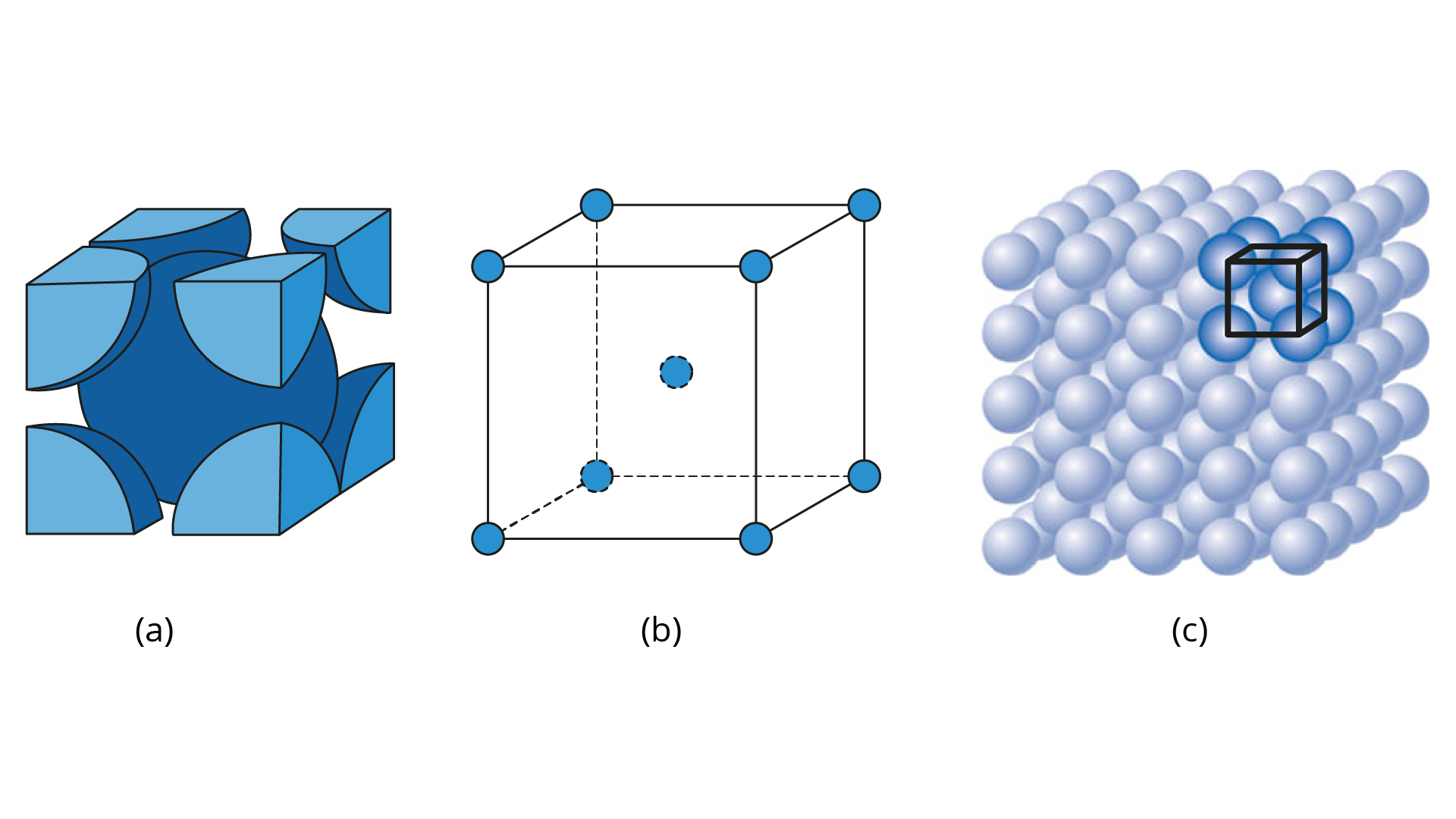
Logo, em uma estrutura cristalina do tipo CCC, teremos o total de dois átomos inteiros dentro da célula unitária.
Com relação à determinação do parâmetro de rede para essa estrutura, temos que: \((4R)^2=a^2+(a\sqrt{2})^2\)
\[16R^2=a^2+2a^2=3a^2\]
\[a^2=(16R^2)/3\]
\[a=(4R)/\sqrt{3}\]
A estrutura hexagonal compacta é representada por uma estrutura em forma de hexágono, que possui o comprimento da aresta “a” e a altura representada pela letra “c” (Figura 2.6).
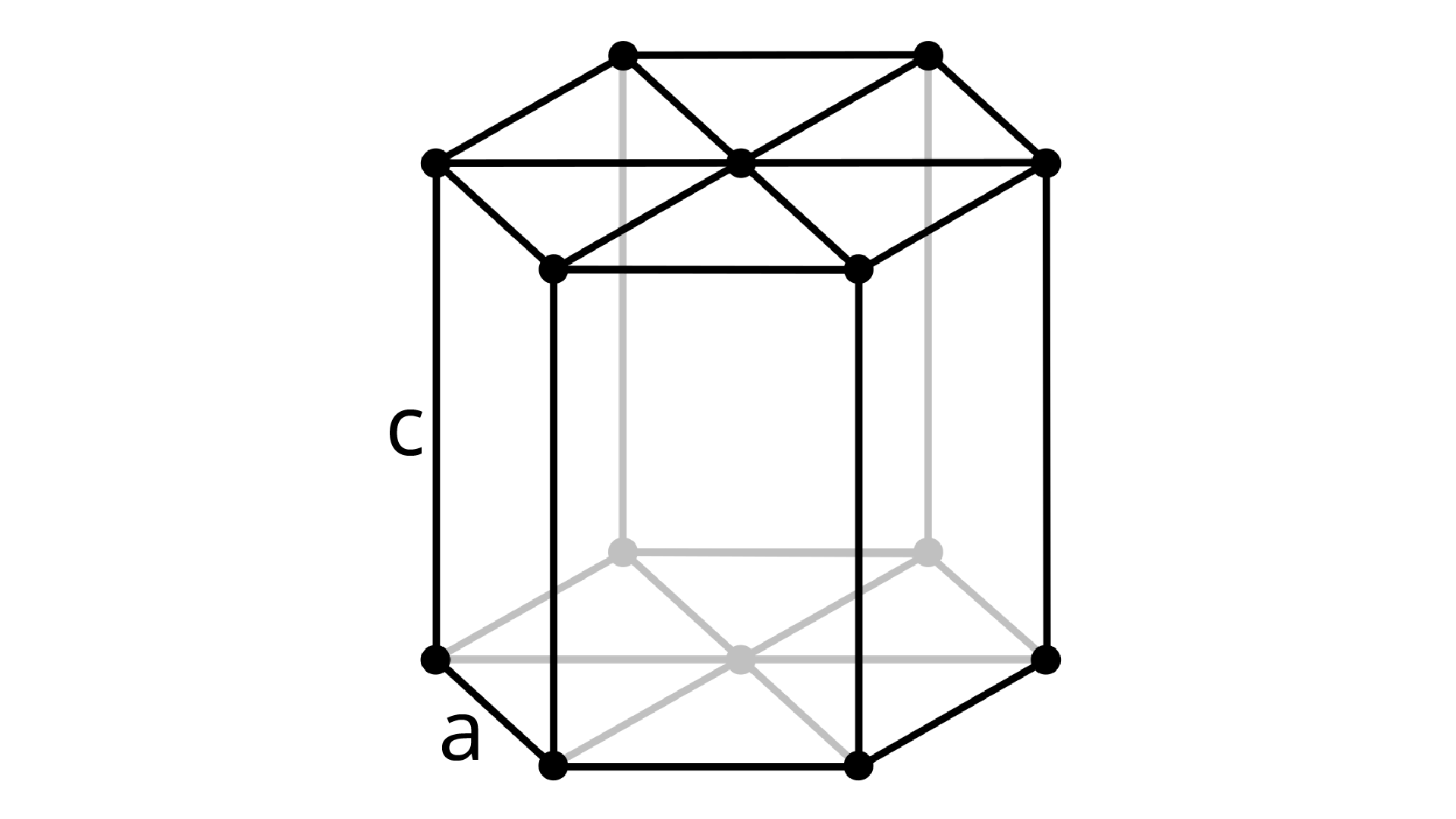
Até agora, temos um total de quatro átomos. Vamos analisar os vértices.
Logo, em uma estrutura do tipo hexagonal compacta, há um total de seis átomos internos.
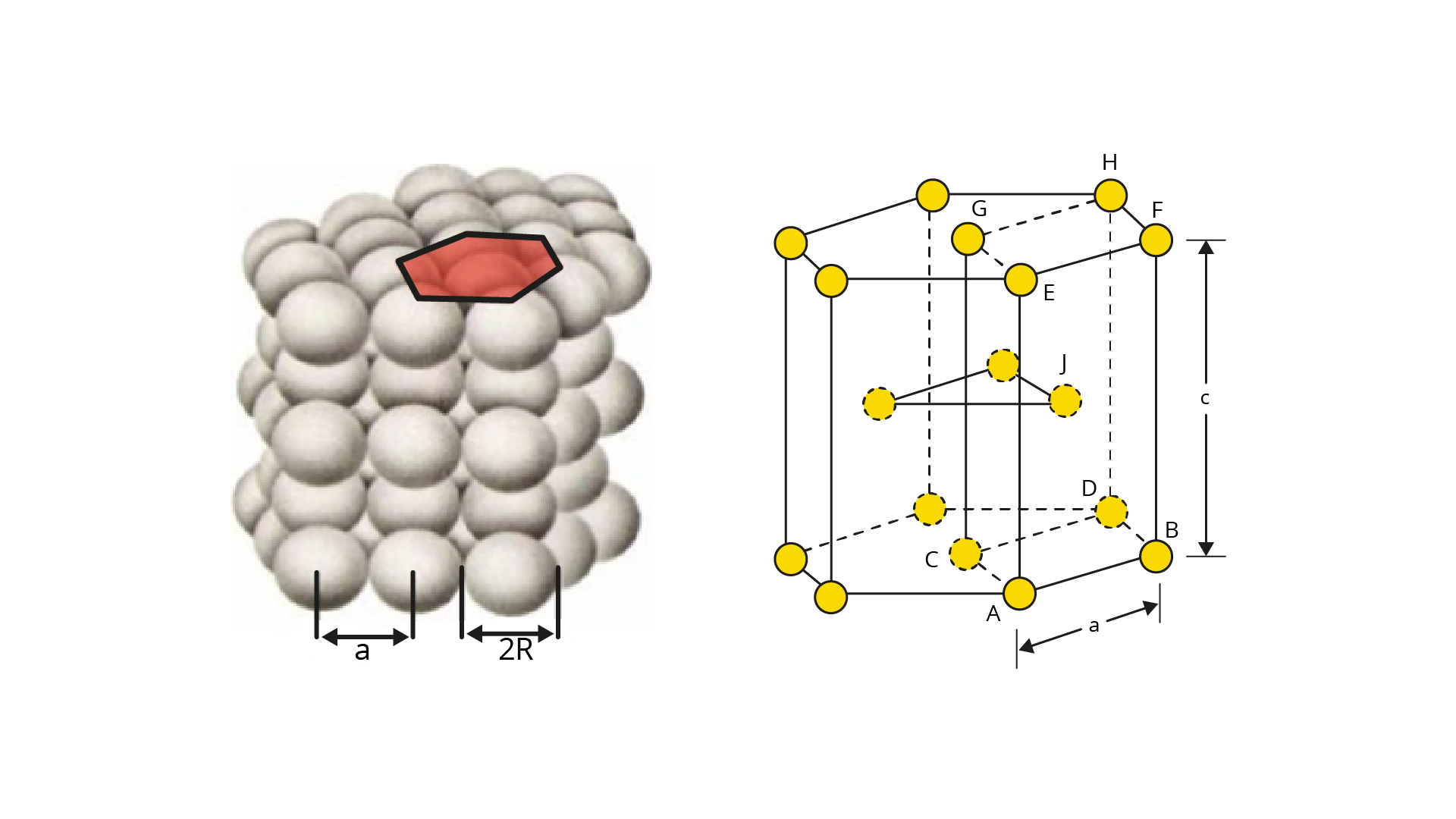
Conforme mostrado na Figura 2.7, existe uma razão entre os valores das arestas “a” e “c” para a estrutura HC, correspondente a c/a ⩬ 1,63, cujo valor é particular para que essa estrutura seja o mais compacta possível, ou seja, para que os átomos estejam o mais próximo possível uns dos outros (CALLISTER JUNIOR; RETHWISCH, 2008).
Por conta da existência de muitas estruturas cristalinas distintas entre si, com diversas configurações de organização, foi necessário agrupá-las mediante seus respectivos arranjos atômicos. A geometria da célula unitária, por exemplo, foi uma das formas de organização que foi definida a partir da forma do paralelepípedo, representando a célula unitária. Em meados do século passado, o cientista francês A. Bravais propôs que o estudo das estruturas cristalinas poderia ser realizado com a utilização de sete sistemas cristalinos básicos e que, partindo deles, seria possível descrever 14 células unitárias, as quais seriam capazes de identificar qualquer tipo de estrutura cristalina conhecida.
Alguns metais, assim como os não metais, podem ter mais de uma estrutura cristalina, um fenômeno conhecido como polimorfismo. Quando encontrada em sólidos elementares, a condição é frequentemente denominada alotropia. A estrutura cristalina depende da temperatura e da pressão externa. Um exemplo conhecido é encontrado no carbono: o grafite é o polimorfo estável nas condições ambientes, enquanto o diamante é formado sob pressões extremamente altas.
Além disso, o ferro puro possui uma estrutura de cristal (CCC) à temperatura ambiente; no entanto, muda sua estrutura para CFC à temperatura de 912 ºC. Na maioria das vezes, uma modificação da densidade e outras propriedades físicas acompanha uma transformação polimórfica.
Em resumo:
Polimorfismo : quando um mesmo material possui mais de uma estrutura cristalina.
Alotropia : quando o polimorfismo é observado em sólidos elementares.
Saiba mais sobre o assunto acessando o link a seguir, a partir da página 3.
Fonte: Adaptado de Muscelli (2012).
No Quadro 1.1, são mostradas as principais características desses sistemas no tocante a parâmetros de rede e ângulos entre eixos (CALLISTER JUNIOR; RETHWISCH, 2008).
O arranjo CFC caracteriza-se por exibir dois átomos nas arestas e mais três átomos no total das faces do cubo. A partir do parâmetro de rede já apresentado nesta unidade, determine o fator de empacotamento da estrutura CFC.
FEA = (16/3) π R3 / 16 R3 √2
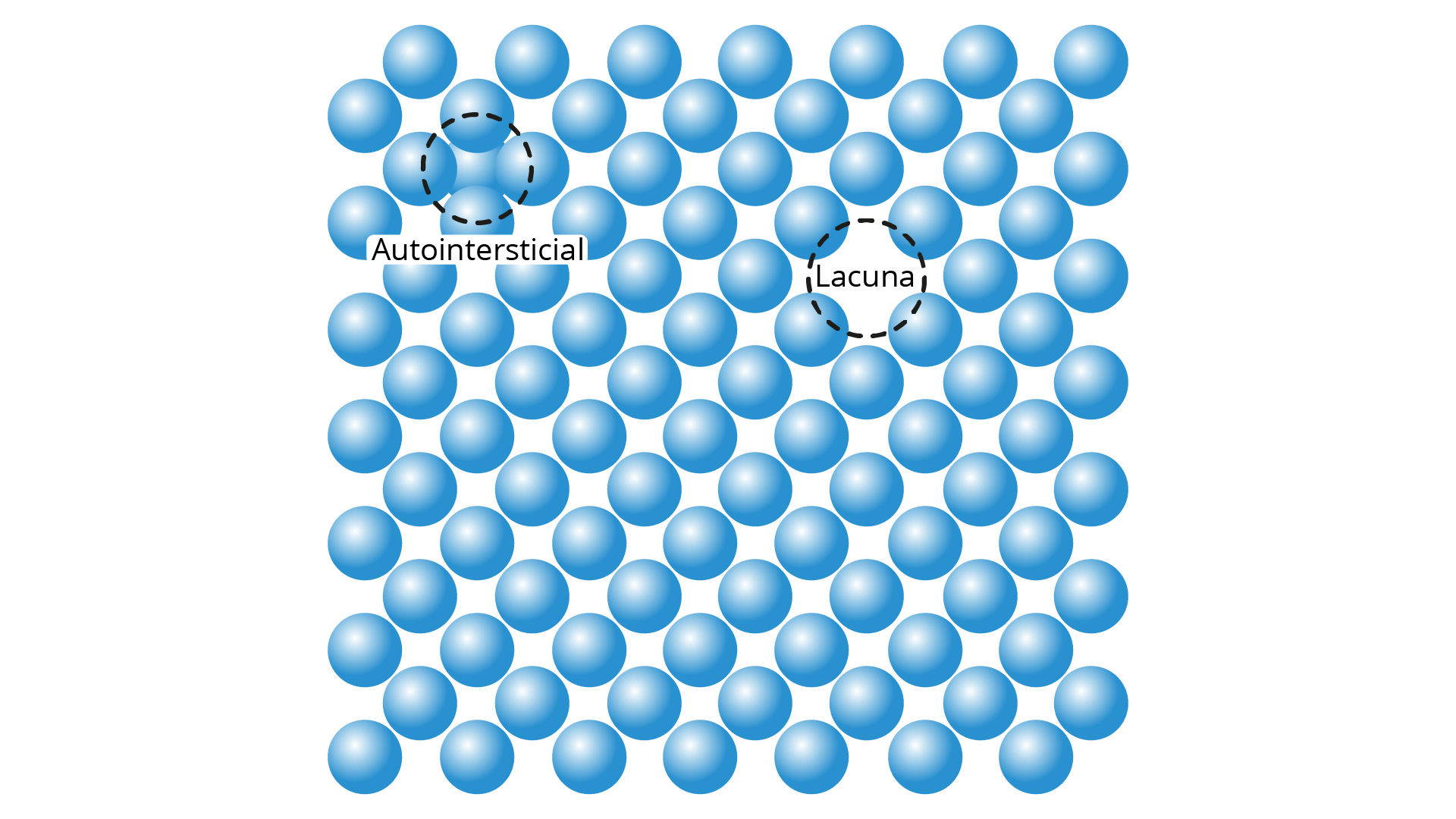
Até o momento, só se considerou a existência de uma ordenação perfeita entre os átomos para um material cristalino; entretanto, como nenhuma estrutura é completamente perfeita, faz-se necessário estudar as imperfeições presentes nos sólidos. Conhecer as imperfeições dos materiais é de fundamental importância para a compreensão do comportamento dos metais, inclusive do efeito que essas imperfeições causam. Todos os materiais possuem uma quantidade variada de imperfeições que impactam em suas propriedades. Esse impacto nem sempre é negativo, e, muitas vezes, características específicas desejadas podem ser alcançadas a partir do controle dessas imperfeições. A rede cristalina também pode possuir o que se chama defeito pontual, que corresponde a uma irregularidade na rede acerca das dimensões na ordem do diâmetro atômico. Entre os diversos defeitos abordados neste capítulo, tem-se, ainda, os defeitos lineares/unidimensionais e os defeitos interfaciais/bidimensionais. Como efeitos relacionados, os átomos de impureza, por exemplo, podem ser defeitos pontuais. A seguir, serão discutidas formas de examiná-los.
Os defeitos pontuais, também definidos como defeitos unidimensionais, estão relacionados a pontos específicos da rede cristalina, em apenas uma dimensão. Esses defeitos podem ser de diferentes tipos e são, geralmente, formados durante o processamento ou durante o processo de crescimento do cristal. Os defeitos pontuais apresentam as seguintes classificações.
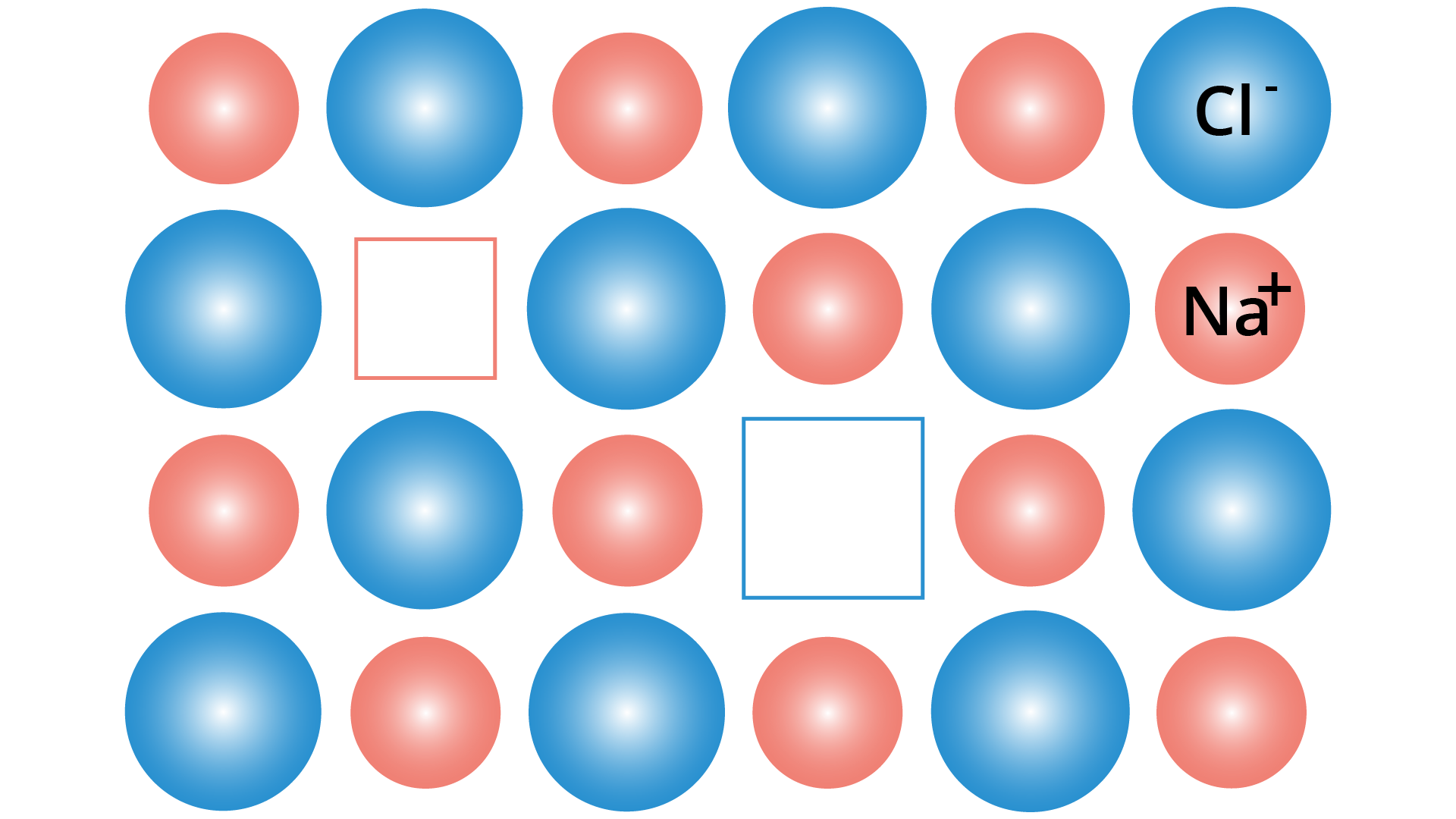
Um defeito de Schottky é um tipo de defeito pontual em uma rede cristalina. Recebeu esse nome devido ao Walter H. Schottky. Nos cristais não iônicos, refere-se a defeitos de vacância da rede. Nos cristais iônicos, esse tipo de defeito pontual se forma quando íons com carga oposta deixam seus locais da rede, criando lacunas. Essas lacunas são formadas em unidades estequiométricas, para manter uma carga neutra. Os átomos ao redor se movem para preencher essas lacunas, causando a formação de novas lacunas.
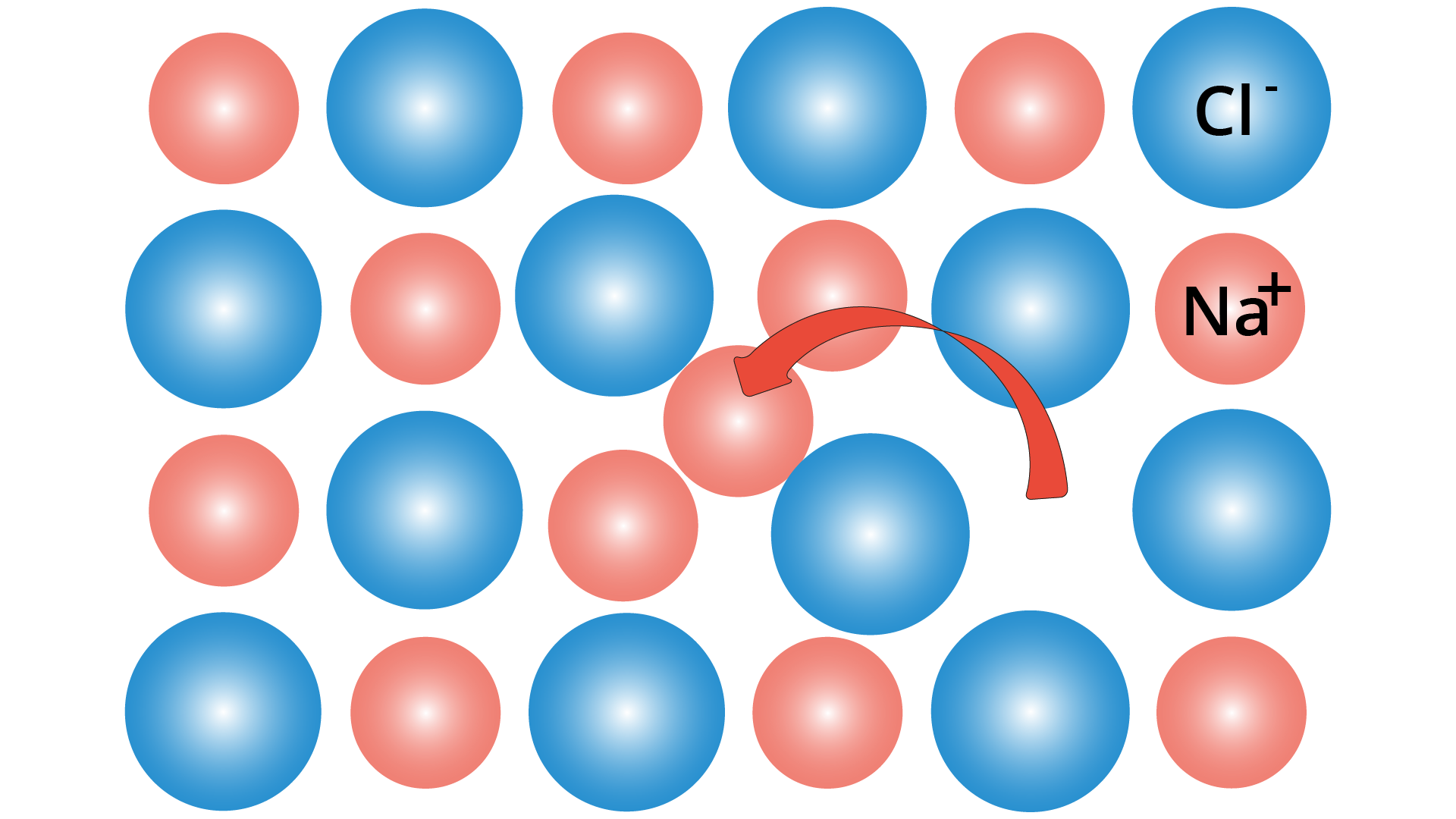
Um defeito de Frenkel, ou defeito de deslocamento, é um tipo de defeito pontual em sólidos cristalinos. Possui esse nome em homenagem ao seu descobridor, Yakov Frenkel. O defeito se forma quando um átomo ou íon menor (geralmente cátion) deixa seu lugar na rede, criando uma lacuna, e se torna um intersticial, por se hospedar em um local próximo.
Devido a limitações fundamentais dos métodos de purificação de materiais, os materiais nunca são 100% puros, o que, por definição, induz a defeitos na estrutura do material cristalino. No caso de uma impureza (defeito), o átomo é frequentemente incorporado em um local atômico regular na estrutura cristalina. Se este não é um local vago e o átomo não estiver em um local intersticial, é chamado de defeito substitucional.
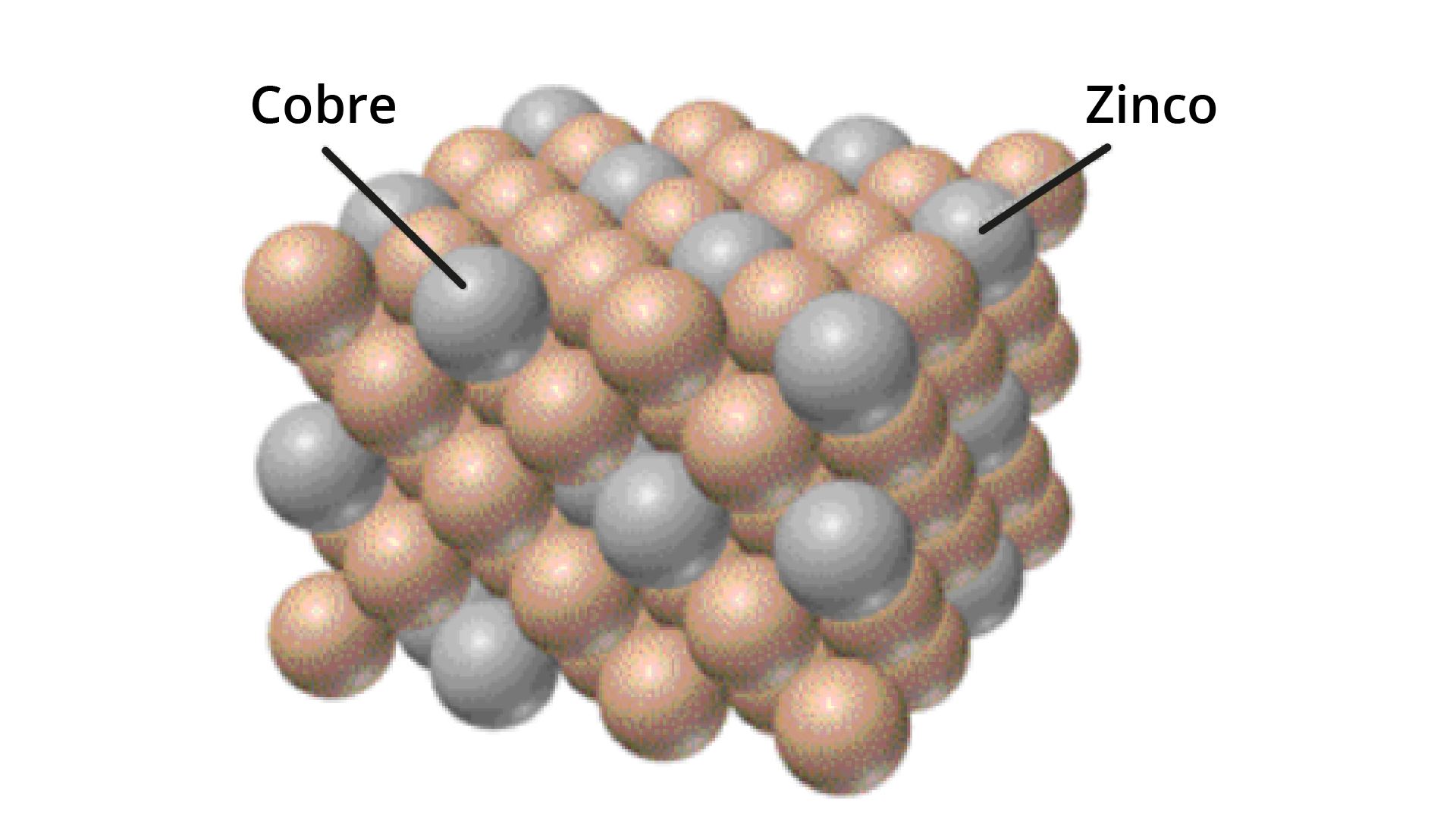
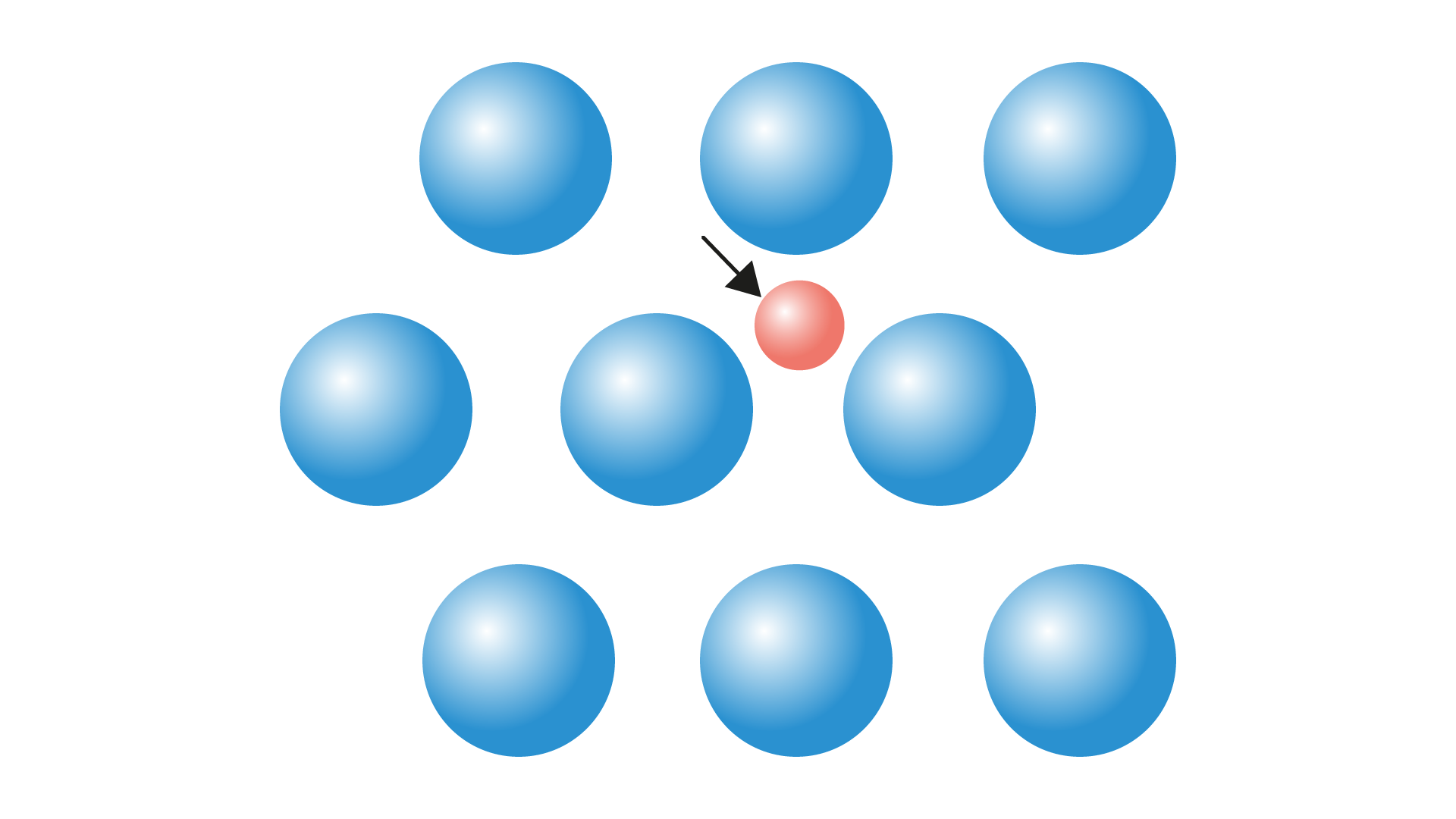
No caso de um átomo que é incorporado em um local atômico irregular na estrutura cristalina, se este fica localizado no “vazio” entre os átomos, é chamado de defeito intersticial.
Os materiais cristalinos podem apresentar defeitos que, muitas vezes, são alinhados e contínuos em sua estrutura, dando origem ao que se chama imperfeições em linha, ou imperfeições unidimensionais. Os defeitos em linha, também chamados de discordâncias, são imperfeições que proporcionam uma distorção da rede cristalina em torno de uma linha e caracterizam-se por envolver um plano extra de átomos. Essas imperfeições podem surgir durante o crescimento do cristal, em processos nos quais ocorre a deformação plástica do material cristalino ou, ainda, como resultado da interação de vacâncias. Existem dois principais tipos de discordâncias, que são conhecidos como discordância em cunha e discordância em hélice.
Estudar as imperfeições dos materiais é fundamental para a compreensão do comportamento, principalmente, dos metais, inclusive em relação ao efeito que essas imperfeições causam neles. A partir dos conhecimentos adquiridos, analise as seguintes sentenças relacionadas à estrutura cristalina dos materiais.
Está correto o que se afirma em:
Muitos dos materiais, quando utilizados, estão sujeitos a forças ou cargas, a exemplo da asa dos aviões, constituídas por uma liga de alumínio, e do eixo de um automóvel, fabricado com aço. Nessas situações, é necessário conhecer as características do material para que se possa projetar a peça utilizando o material adequado, de modo que qualquer deformação resultante não seja superior àquela que o material suporta e, consequentemente, não ocorram fraturas. O comportamento mecânico de um material corresponde à relação entre sua resposta ou deformação a uma carga ou força aplicada. Entre as principais propriedades mecânicas dos metais, destacam-se a resistência, a dureza, a ductilidade e a rigidez (GARCIA; SPIN; SANTOS, 2010).
As propriedades mecânicas são motivos de preocupação para várias partes (por exemplo, produtores e consumidores de materiais, organizações de pesquisa, agências governamentais) que têm interesses diferentes. Consequentemente, é imperativo que exista alguma consistência na maneira com que os testes são realizados, bem como nas suas respectivas interpretações dos resultados. Essa consistência é obtida usando técnicas de teste padronizadas. O estabelecimento e a publicação desses padrões são frequentemente coordenados por sociedades profissionais. Nos Estados Unidos, a organização mais ativa é a Sociedade Americana de Testes e Materiais (ASTM). Seu Livro Anual de Normas ASTM compreende numerosos volumes, que são emitidos e atualizados anualmente. Um grande número desses padrões refere-se a técnicas de teste mecânico (CALLISTER JUNIOR; RETHWISCH, 2008).
O papel dos engenheiros estruturais consiste em determinar as tensões e as distribuições de tensões nos membros sujeitos a cargas bem definidas. Isso pode ser realizado por técnicas de teste experimental e/ou por análises de estresse teórico e matemático. Esses tópicos são tratados na análise tradicional de estresse e na força dos textos dos materiais. Os engenheiros estão preocupados em fabricar materiais para atender aos requisitos de trabalho, conforme previsto por essas análises de tensão. Para tanto, é necessária a compreensão das correlações entre a microestrutura (isto é, características internas) dos materiais e suas propriedades mecânicas.
Este tópico discute os comportamentos de tensão-deformação de metais, cerâmicas e polímeros além de suas respectivas propriedades mecânicas.
O módulo de elasticidade é dado pela inclinação da curva tensão-deformação na região em que a deformação é puramente elástica, ou seja, na parte inicial do diagrama, na qual se tem apenas uma reta (GARCIA; SPIN; SANTOS, 2010).
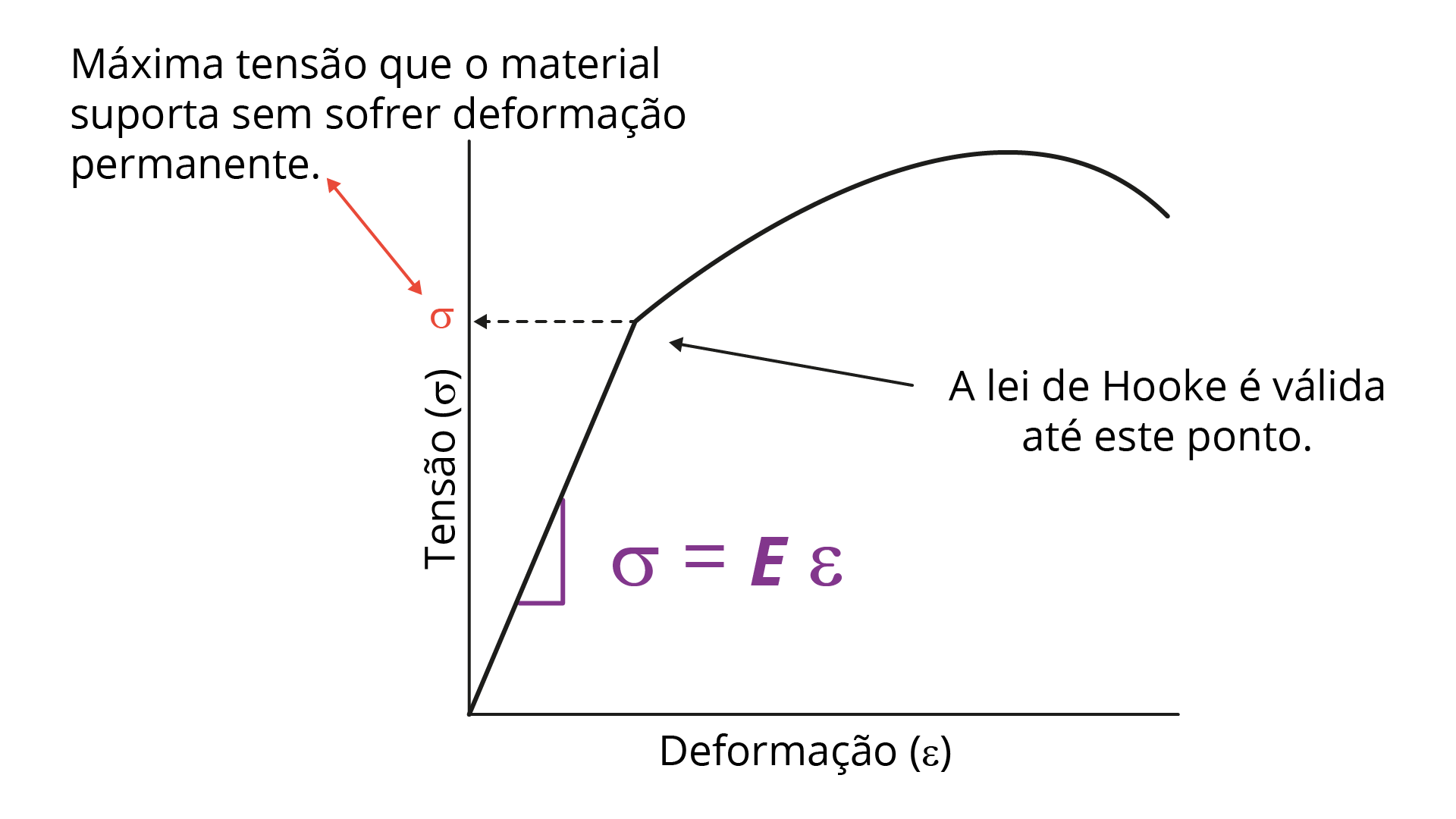
A Figura 2.13 mostra o diagrama de tensão-deformação, com destaque para o módulo de elasticidade, parte do diagrama em que se tem apenas um regime linear. Assim, o módulo pode ser determinado pela equação \(E=\frac{\sigma}{\epsilon}\)
O módulo de resiliência é dado pela área abaixo da curva tensão-deformação, na região em que a deformação é puramente elástica, e representa a quantidade de energia que o sólido é capaz de absorver deformando-se de forma puramente elástica. Depois, a remoção da carga permite a recuperação dessa energia.
A Figura 2.14 mostra o diagrama de tensão-deformação, explicitando o módulo de resiliência.
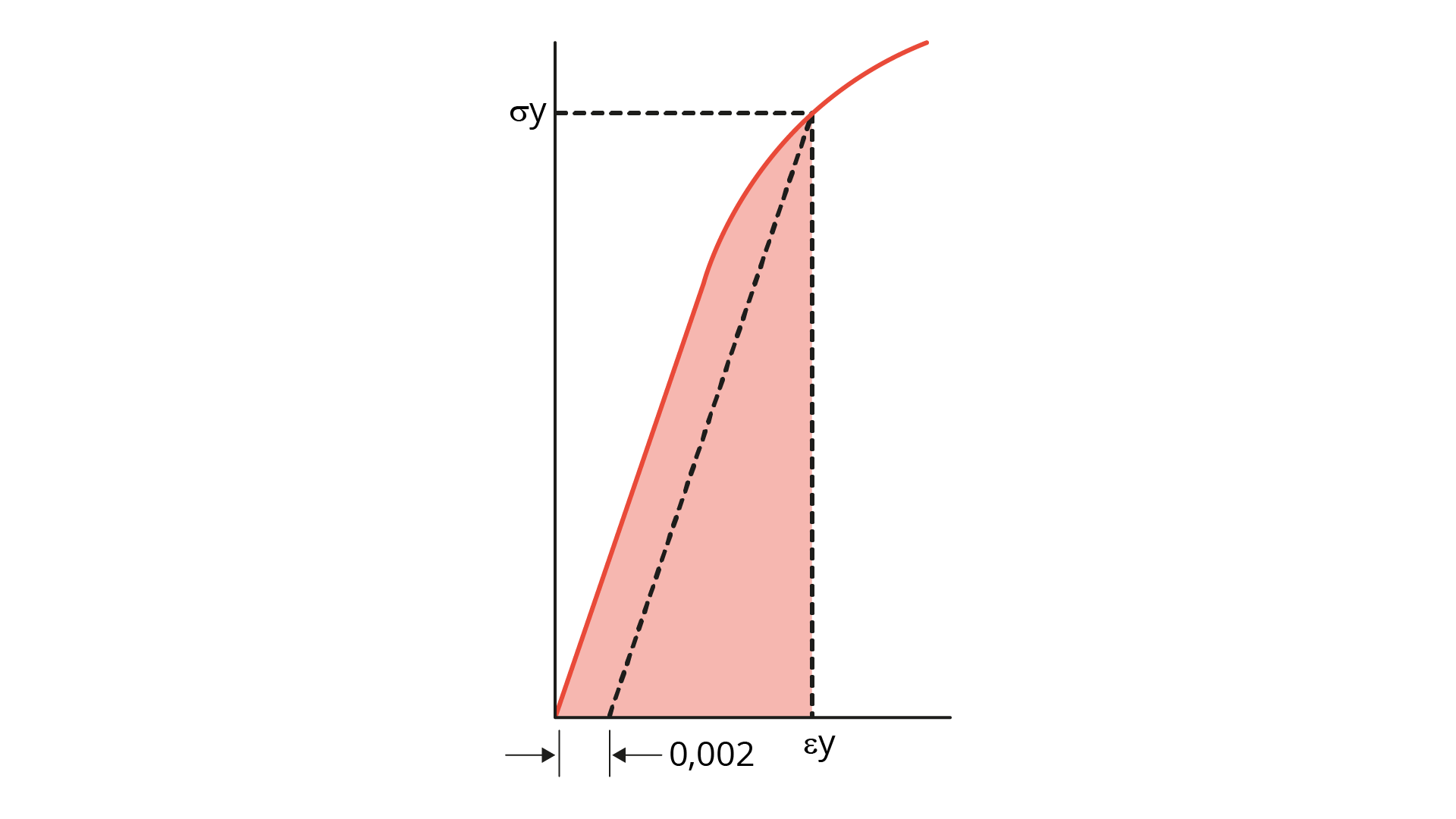
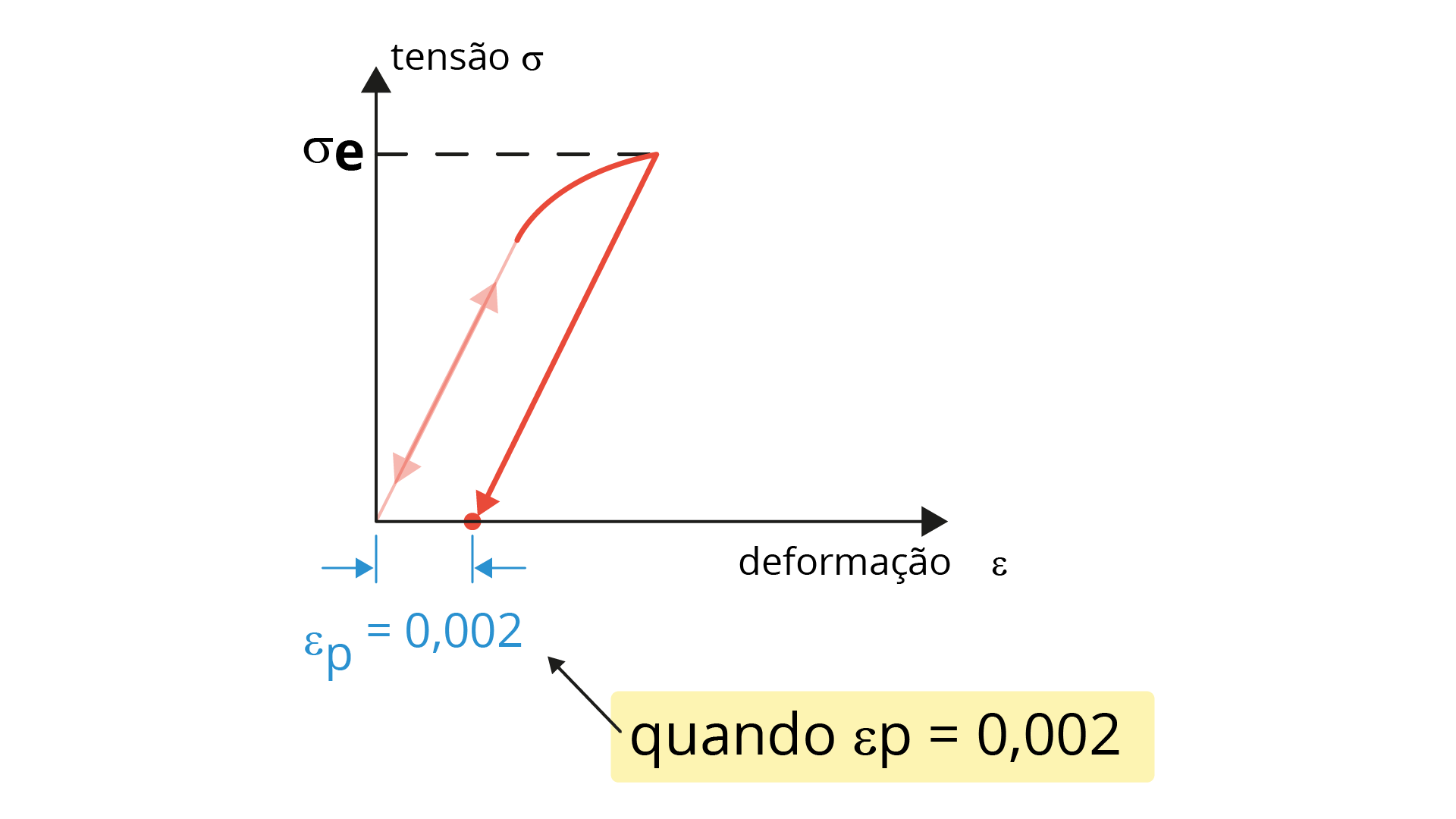
O limite de escoamento (LE) é definido a partir do valor de tensão no qual a deformação deixa de ser apenas elástica. Logo acima deste valor de tensão, conhecido como limite de proporcionalidade, já ocorre uma deformação plástica, ou seja, o material não tem mais a possibilidade de retornar ao seu comprimento inicial. Na prática, é difícil definir esse limite de proporcionalidade com precisão, de modo que é mais prático definir uma tensão conhecida como LE (𝜎e) como sendo a tensão necessária para se produzir uma pequena deformação plástica (𝜀p= 0,002). A Figura 2.15 mostra um diagrama de tensão-deformação, explicitando o LE de um material qualquer.
O limite de resistência (LR), ou limite de resistência à tração (LRT), é definido como a máxima tensão de engenharia analisada durante o ensaio de tração, ou seja, simplesmente o valor máximo de tensão atingido durante o ensaio. A Figura 2.16 representa um diagrama tensão-deformação, apresentando o LR de um determinado material.
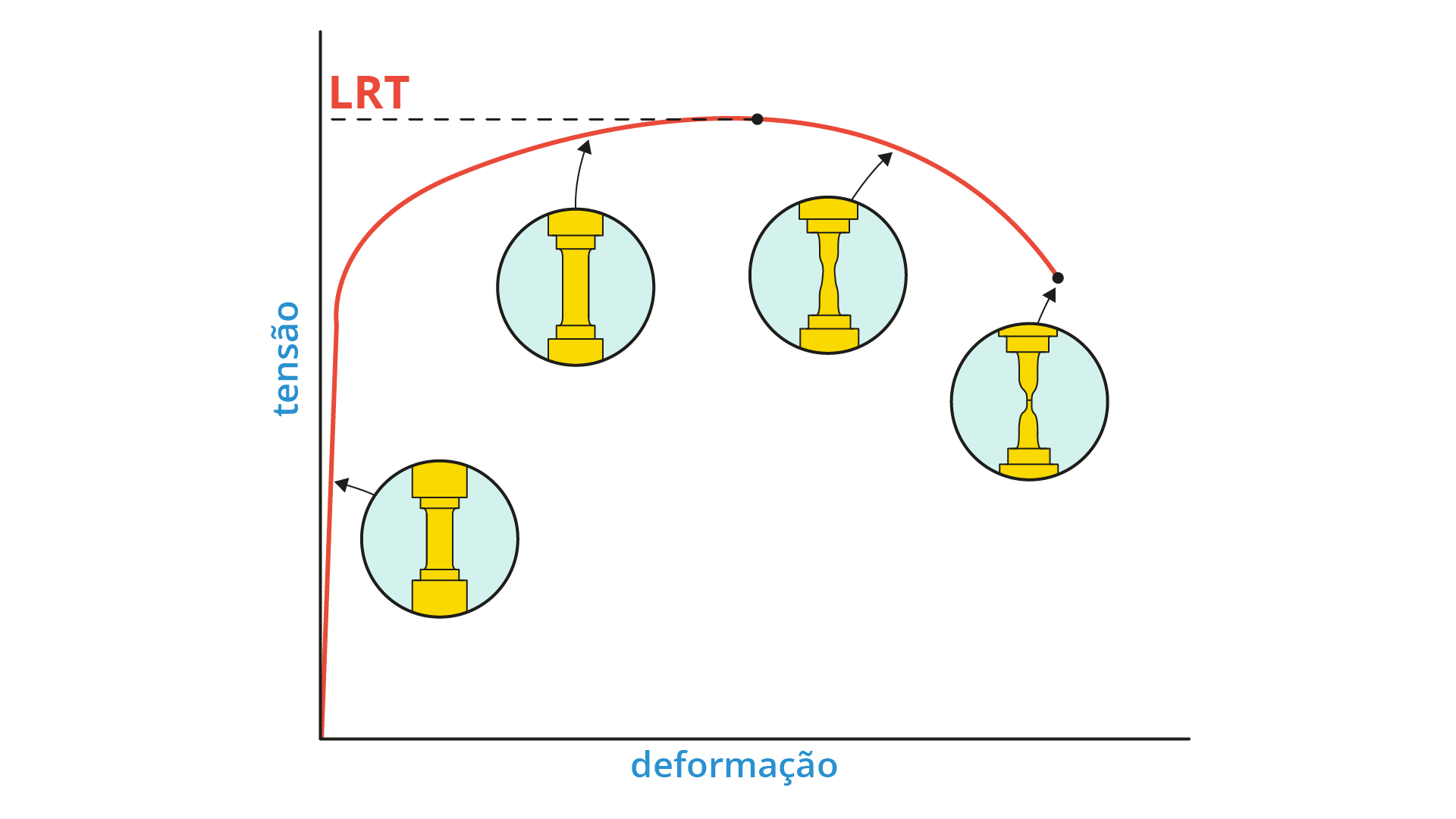
Pode-se identificar o tipo do material ensaiado a partir do local, no diagrama, em que ocorrer o LR.
A ductilidade representa a medida do grau de deformação plástica a qual o material suportou até a fratura. Caso tenha suportado uma pequena deformação plástica ao romper, este material é classificado como frágil ; porém, se suportou uma grande deformação plástica ao romper, trata-se de um material dúctil (GARCIA; SPIN; SANTOS, 2010). A Figura 2.17 mostra um diagrama tensão-deformação, apresentando a ductilidade de materiais do tipo: frágil, com pequena porcentagem de alongamento (%Al abaixo de 5%), e dúctil (se %Al for maior que 5%).

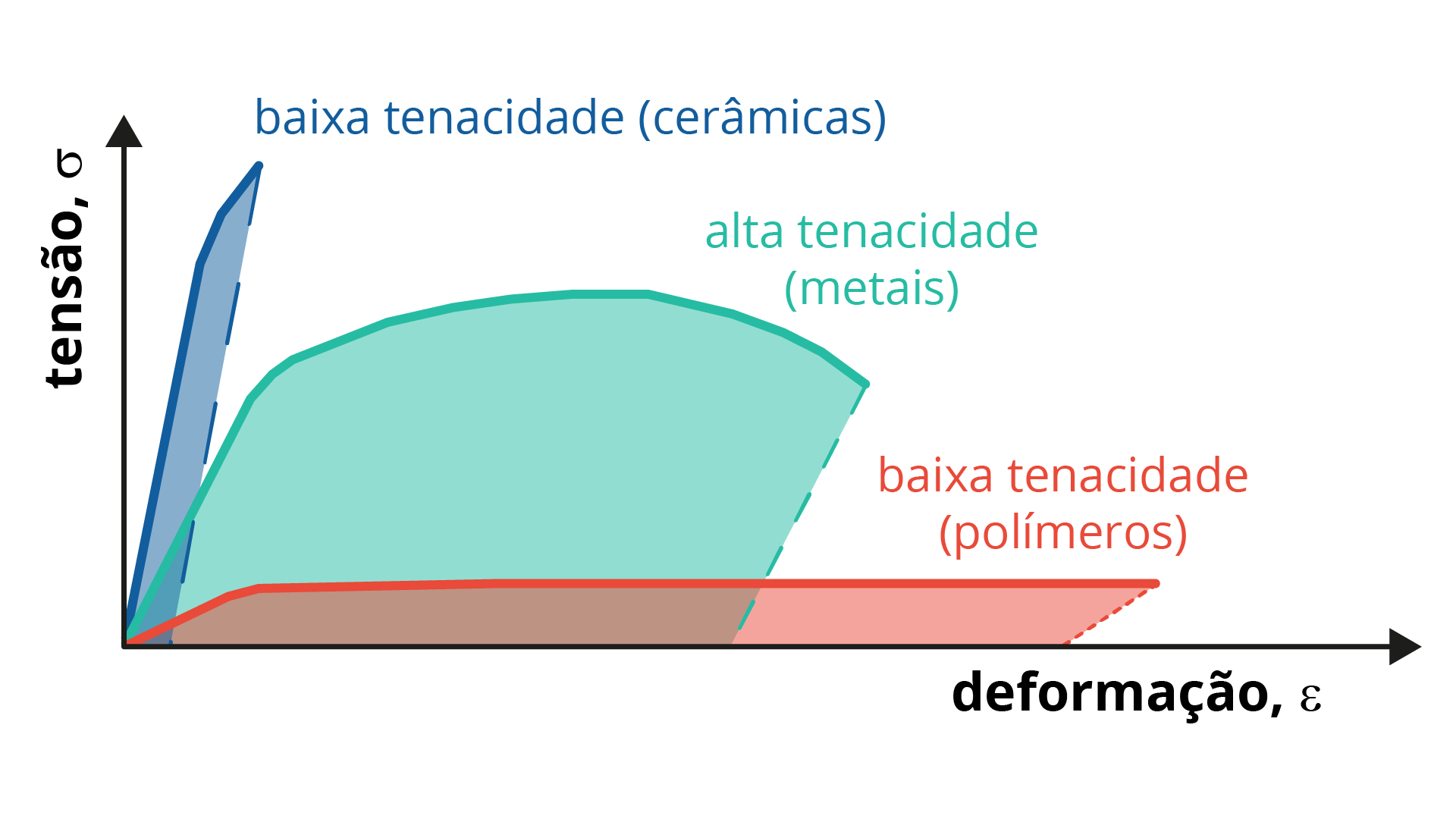
A tenacidade é uma medida da quantidade de energia absorvida por um material quando ele se deforma até a fratura, ou seja, é a energia total relacionada à deformação elástica, somada à deformação plástica, e é indicada pela área total sob a curva tensão-deformação de engenharia do ensaio de tração, ou seja, pode ser medida a partir da área sob a curva “tensão x deformação” até o ponto de ruptura (GARCIA; SPIN; SANTOS, 2010).
Baixa tenacidade, mesmo apresentando elevado módulo de elasticidade, possuem baixo alongamento;
Alta tenacidade, pois apresentam elevado módulo de elasticidade e elevado alongamento;
Baixa tenacidade, mesmo apresentando alongamento muito elevado, apresentam baixo módulo de elasticidade.
A Figura 2.18 mostra o diagrama tensão-deformação, apresentando a tenacidade para três diferentes tipos de materiais.
A dureza é a resistência de um material à deformação localizada, seja ao risco ou ao atrito. Considera-se o material mais duro aquele que é capaz de riscar o outro, por exemplo, se eu preciso lixar ou polir um diamante é necessário de outro diamante que seja tão duro quanto ele para realizar tal efeito. Dessa forma, a fim de quantificar a dureza de um mineral, utiliza-se a escala de Mohs, que é formada por dez minerais organizados em ordem crescente de dureza, que vai do material menos duro (talco) até o mais duro (diamante) (Figura 2.19).
Outra maneira de avaliar a dureza de um material é testar a sua capacidade de ser ou não penetrado (indentado) por outro.
Segundo Dias, Miranda e Godoy (2009), “o teste de indentação Vickers tem sido muito utilizado para avaliação da dureza superficial em diferentes tipos de materiais. Devido à sua versatilidade, esta metodologia também é utilizada para avaliar diferentes propriedades mecânicas, como o módulo de Young (E) e a tenacidade à fratura (KIC), principalmente em materiais sinterizados como, por exemplo, o carboneto de tungstênio com cobalto (WCCo)”.
Esse é um dos exemplos de milhares de trabalhos publicados que apresentam dados do teste de indentação. Reflita sobre o assunto.
Fonte: Dias, Miranda e Godoy (2009).
O ensaio de indentação, ou ensaio de dureza, consiste em escolher uma ponta, com todas suas características previamente conhecidas, e fazê-la penetrar no material cuja dureza se deseja conhecer, aplicando uma carga (força) conhecida (GARCIA; SPIN; SANTOS, 2010).
O comportamento mecânico de um material corresponde à relação entre sua resposta ou deformação a uma carga ou força aplicada. Considere que a curva apresentada na figura a seguir corresponde à curva de tensão versus deformação de engenharia de um aço comumente empregado nas construções.
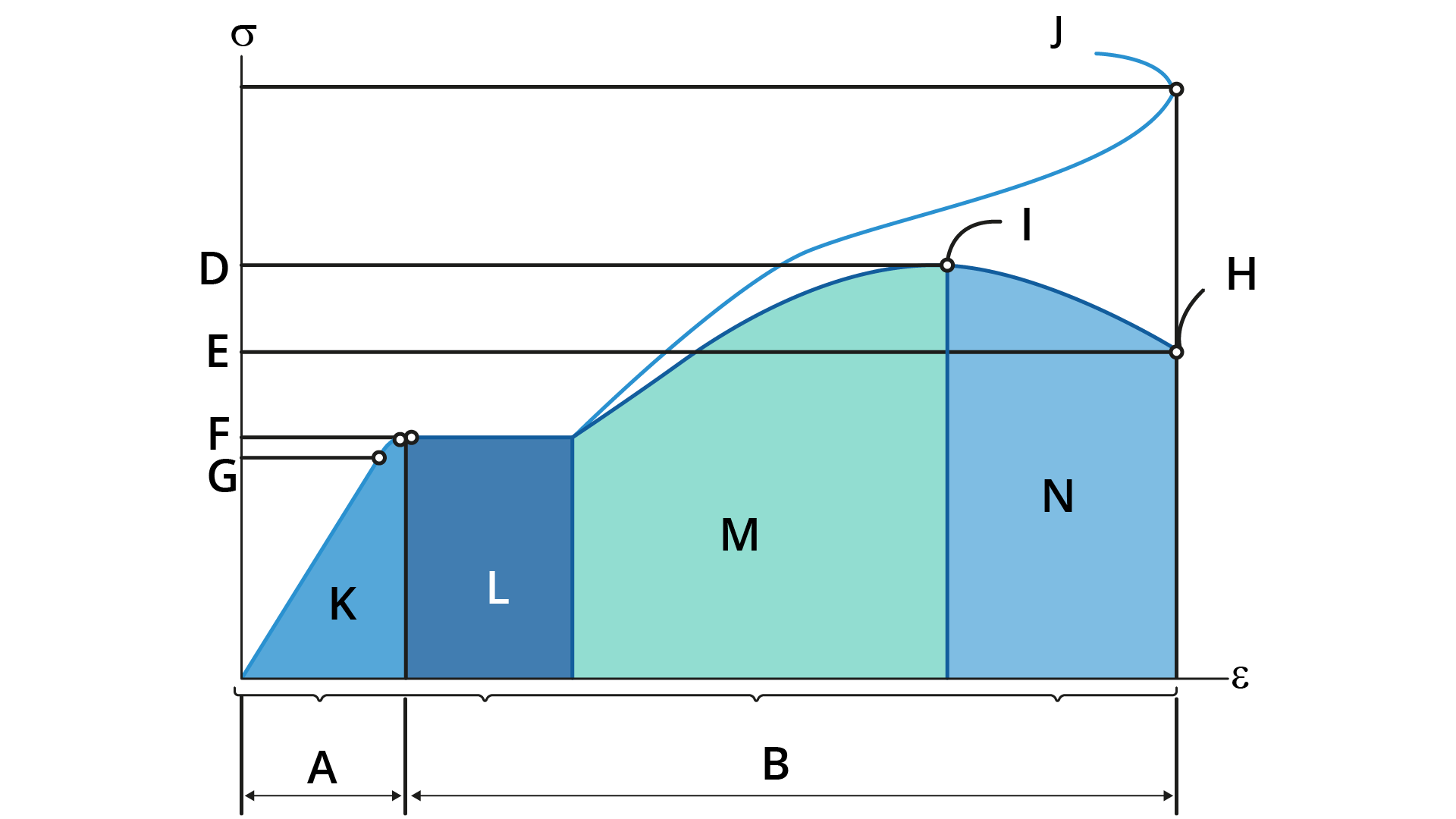
Considerando o diagrama apresentado, avalie as afirmações a seguir.
Está correto o que se afirma em:
A compreensão do diagrama de fases é imprescindível para a engenharia, pois é importante conhecer as propriedades dos materiais para a correta execução de um projeto e o controle dos procedimentos. As microestruturas e as propriedades mecânicas estão relacionadas entre si, e o diagrama de fases oferece informações acerca dessa relação e dos fenômenos aos quais são submetidos os materiais. Este tópico objetiva apresentar as terminologias que estão ligadas aos diagramas de fases e às suas transformações, os diagramas de pressão-temperatura para materiais puros, a interpretação desses diagramas, os diagramas mais recorrentes e as microestruturas de equilíbrio sob diversas circunstâncias (VAN VLACK, 1984).
Para falarmos sobre ligas, fases e equilíbrio, é preciso se apropriar de algumas terminologias comuns do diagrama de fases. Os componentes serão apresentados como metais puros e/ou compostos que compõem uma determinada liga. Um sistema pode ser compreendido como um corpo específico de um material específico ou pode ser uma série de possíveis ligas compostas pelos mesmos componentes, de maneira independente à composição da liga (CALLISTER JUNIOR; RETHWISCH, 2008).
O limite de solubilidade pode ser definido como o ponto máximo em que um sistema de ligas, sob uma determinada temperatura, pode se dissolver em um solvente. A adição excessiva do soluto gera uma outra formação ou um novo composto que não o esperado. O exemplo mais simples apresentado para ilustrar o limite de solubilidade é o da água e do açúcar. Até um dado momento, o açúcar (soluto) na água é plenamente dissolvido e compõe um xarope (CALLISTER JUNIOR; RETHWISCH, 2008). No entanto, a partir de uma dada quantidade, o açúcar já não se dissolve plenamente no solvente (água), gerando a composição de xarope e cristais de açúcar que não foram dissolvidos. A Figura 2.20 mostra o efeito da temperatura nessa relação de solubilidade.
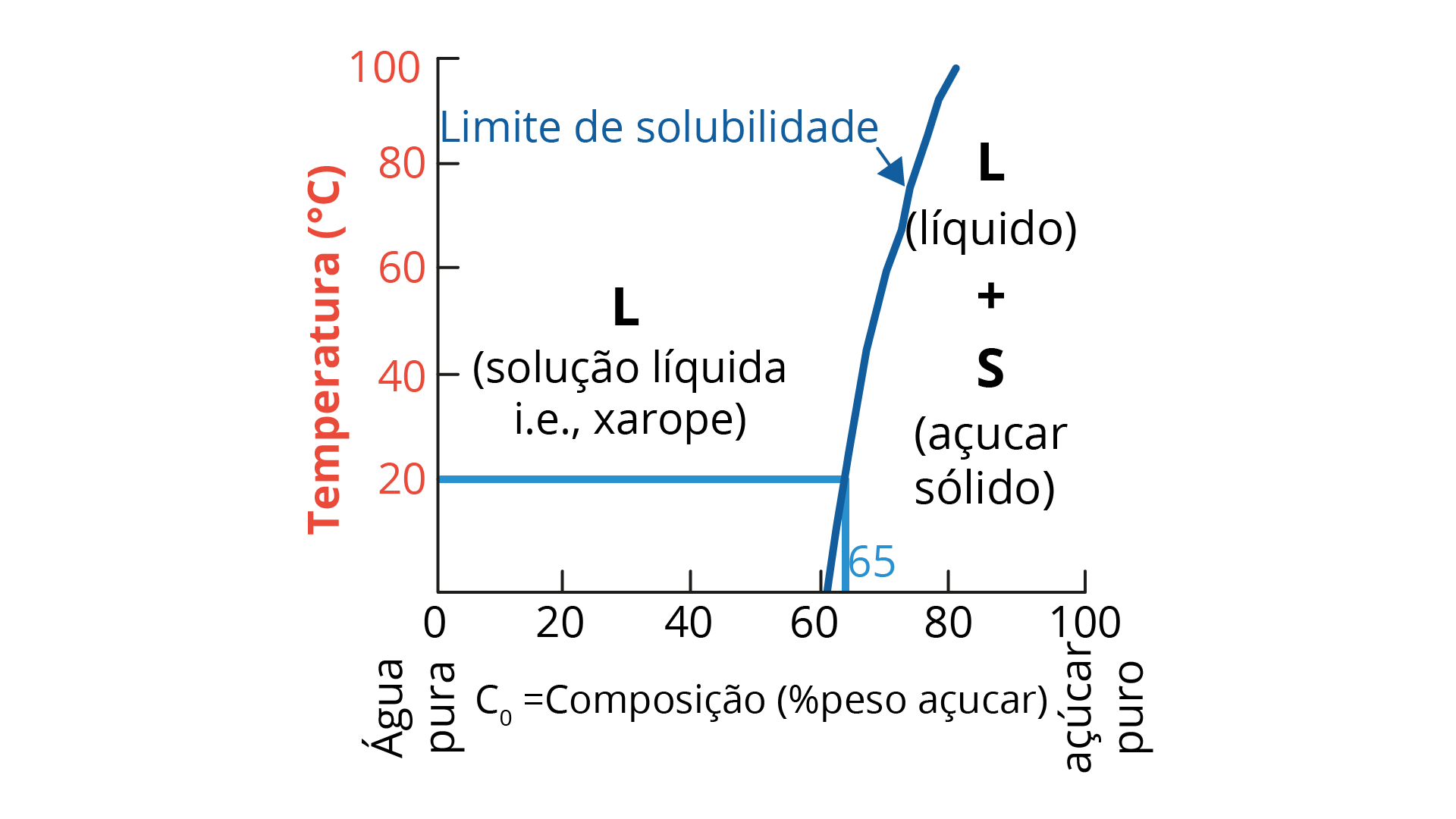
O conceito de fase é determinante para a compreensão do diagrama de fases. Em uma fase, é possível identificar uma porção homogênea de um sistema com características semelhantes e uniformes, química e fisicamente. Os materiais puros são considerados unifásicos, assim como as soluções em estado líquido, sólido ou gasoso. Para cada fase, haverá características próprias, com propriedades físicas e químicas distintas. Mesmo que haja diferentes fases em um mesmo sistema, para cada uma delas haverá propriedades individuais, e será possível observar uma mudança brusca que as separam uma das outras. Nesses casos de diferentes fases em um mesmo sistema, a mera distinção em relação a uma das propriedades (seja ela física ou química) já implica a separação entre elas, não sendo necessário que haja diferença nas duas. Os sistemas heterogêneos, como são conhecidos os sistemas compostos por duas fases ou mais, contemplam a maioria das ligas metálicas e os sistemas cerâmicos, poliméricos e compósitos.
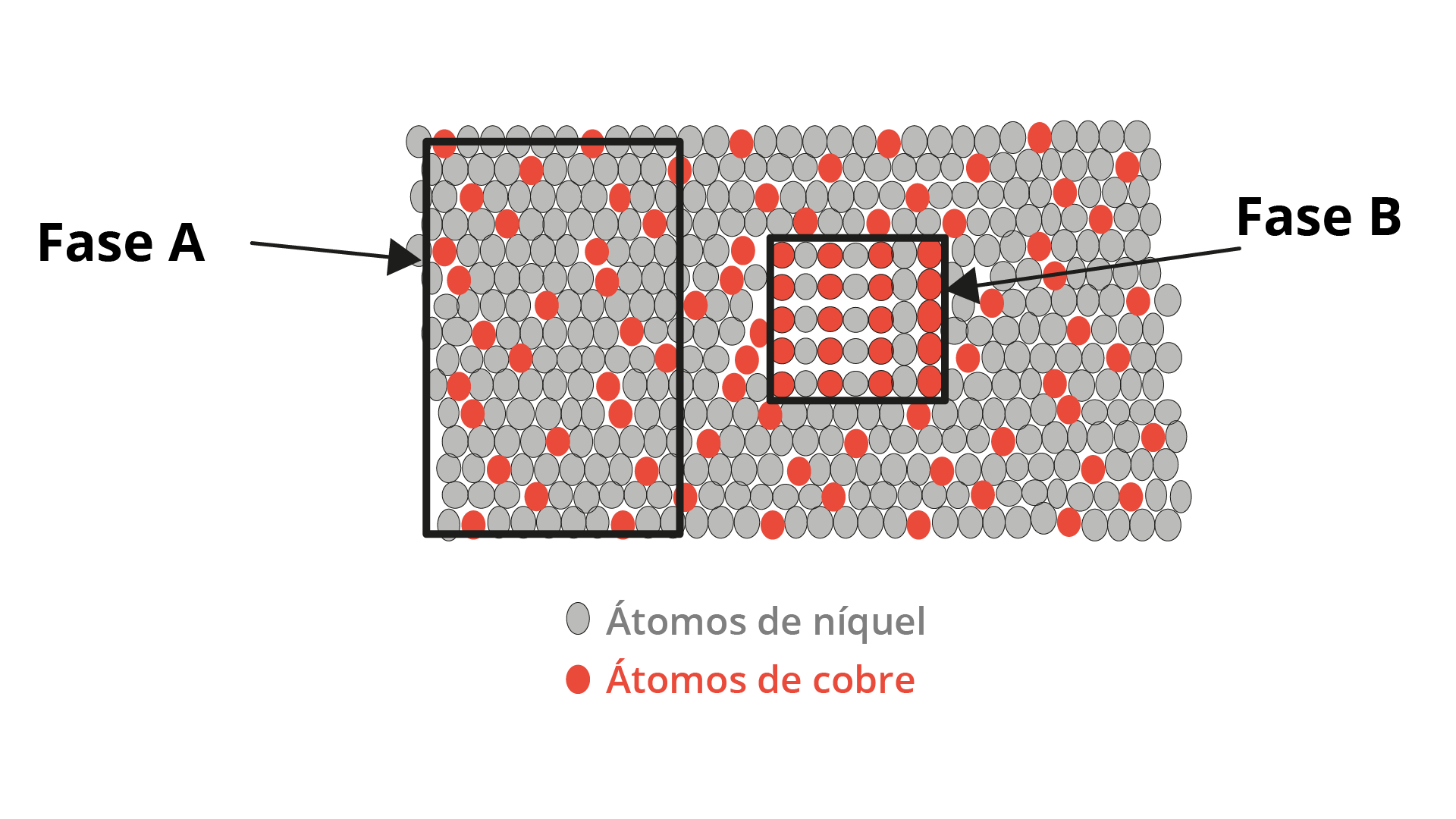
O próprio sistema multifásico gera, devido à interação entre as fases, características diferentes e mais atrativas do que as de uma fase separada (CALLISTER JUNIOR; RETHWISCH, 2008) (Figura 2.21).
Compreendendo o conceito de fase, fica mais simples a definição da microestrutura, uma vez que essa é caracterizada pela quantidade de fases, suas propriedades e proporções, bem como pela maneira como se organizam e se distribuem. A microestrutura só pode ser observada a partir do auxílio de aparelhos ópticos e eletrônicos. A microestrutura de uma liga está diretamente relacionada aos elementos contidos nela, assim como às suas concentrações e ao tratamento térmico dado (GARCIA; SPIN; SANTOS, 2010). A Figura 2.22 mostra uma microestrutura de liga chumbo-estanho com duas fases distintas.

No estudo das ligas, em especial as ligas metálicas, é muito importante a identificação das fases e da sua microestrutura. Parte desse estudo consiste na determinação da quantidade relativa de uma fase para uma dada condição, o que é realizado utilizando a regra da alavanca . A Figura 2.23 representa o diagrama de fases de uma liga hipotética do sistema A-B, com a aplicação da regra da alavanca.
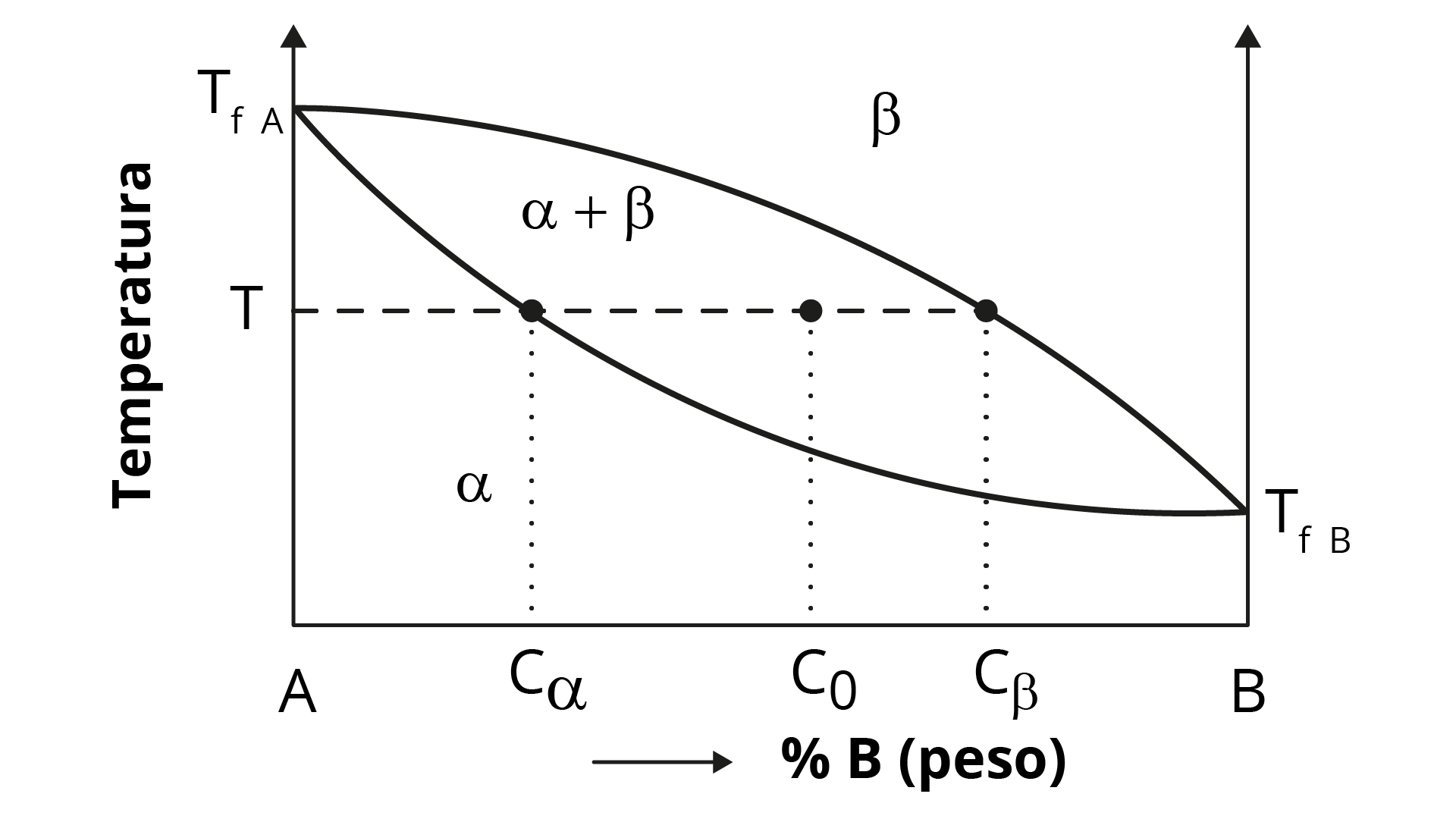
A partir do diagrama que possui duas fases, alfa (𝛼) e beta (𝛽), e da aplicação da regra da alavanca, pode-se determinar a quantidade de cada fase utilizando as equações a seguir.
\[\text{%}\alpha =\frac{C\beta ~-C{{o}_{{}}}}{C\beta ~-C{{\alpha }_{{}}}}~x~100\text{%}\]
\[\text{%}\beta =\frac{C𝛼~-C{{o}_{{}}}}{C\beta ~-C{{\alpha }_{{}}}}~x~100\text{%}\]
onde:
Co: concentração da liga;
C𝛼: concentração de B na fase 𝛼
C𝛽: concentração de B na fase 𝛽
%α: quantidade relativa da fase 𝛼
%β: quantidade relativa da fase 𝛽 (CALLISTER JUNIOR; RETHWISCH, 2008).
O diagrama de fases do sistema de ferro-carbeto de ferro é, possivelmente, de todos os sistemas de ligas binárias, o mais importante. Esse diagrama está representado na figura a seguir.
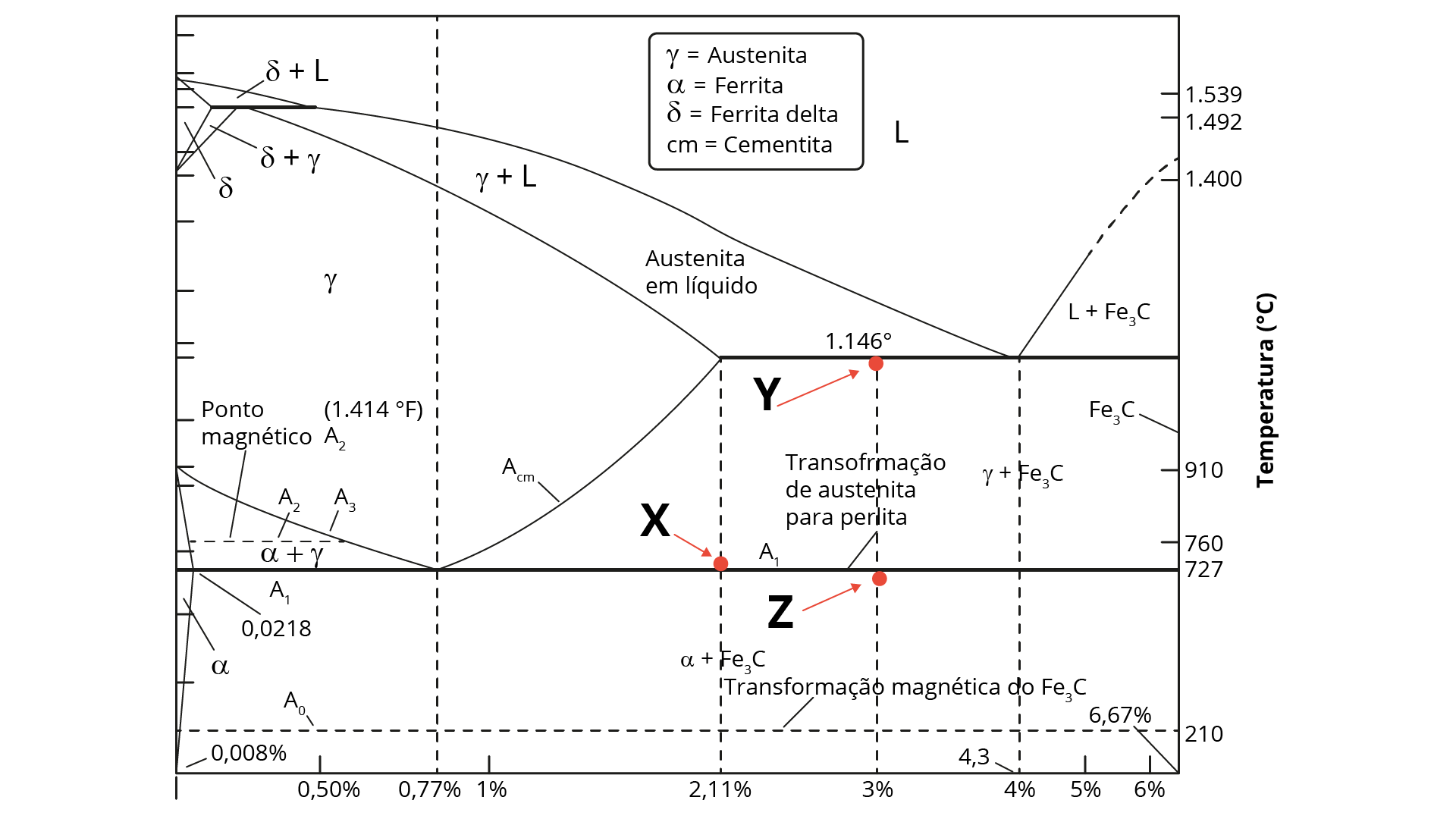
Considerando o diagrama de fase apresentado, analise as afirmações a seguir.
Está correto o que se afirma em:

William F. Smith e Javad Hashemi
Editora: AMGH
Edição : 5
ISBN: 13: 978-8580551143
Comentário: O livro, já na versão em português, é de grande ajuda na compreensão dos conteúdos abordados nesta unidade. Para o tema de diagramas de fases, em em especial, recomenda-se a leitura do capítulo 8.

Ano: 2004
Comentário: O filme apresenta um resumo sobre a produção do aço em escala industrial e faz uma relação com todo o avanço tecnológico que a humanidade obteve a partir do domínio das técnicas de fabricação e processamento dos aços.
Para conhecer mais sobre o filme, acesse o trailer disponível. Acesso em: 27 jan. 2020.
Esta unidade apresentou uma breve visão sobre a estrutura básica dos materiais cristalinos, que se formam a partir de uma unidade básica conhecida como célula unitária, formando, na sequência, um sistema cristalino e, depois, o que chamamos de estrutura cristalina, bem as diferenças entre os materiais cristalinos e amorfos. Durante a formação dos materiais, sempre haverá a presença de defeitos, que nem sempre irão proporcionar ao material características negativas, sendo sua presença desejada, sejam eles pontuais, lineares ou de outros tipos. Na seção que apresenta as propriedades mecânicas, foi apresentada a tensão e a deformação, em especial as propriedades relacionadas com o ensaio de tração, a exemplo do comportamento elástico - comportamento reversível, que comumente mostra uma relação linear entre a tensão e a deformação e do comportamento plástico -, que resulta em deformação permanente quando a tensão atinge um valor suficiente para provocar o deslizamento das discordâncias.
CALLISTER JUNIOR, W. D.; RETHWISCH, D. G. Ciência e engenharia de materiais: uma introdução. 7 ed. Rio de Janeiro: LTC editora, 2008.
DIAS, A. M. S.; MIRANDA, J. S.; GODOY, G. C. Avaliação da tenacidade à fratura através do ensaio de indentação em pastilhas de metal duro. Revista Matéria , v. 14, n. 2, p. 869-877, 2009. Disponível em: http://www.scielo.br/pdf/rmat/v14n2/a09v14n2 . Acesso em: 20 jan. 2020.
ESCOLA Politécnica da Universidade de São Paulo. Defeitos do sólido cristalino: difusão no estado sólido. São Paulo, 2014. (Slides). Disponível em: https://bit.ly/2uE1Ob8 . Acesso em: 20 jan. 2020.
GARCIA, A.; SPIN, J. A.; SANTOS, C. A. Ensaios dos materiais. Rio de Janeiro: LTC editora, 2010.
MUSCELLI, W. C. Preparação e caracterização de materiais de carbono via termopolimerização de pré-polímero fenol-formaldeído. 2012. 85f. Dissertação (Mestrado em Ciências) - Universidade de São Paulo, Ribeirão Preto, 2012. Disponível em: https://teses.usp.br/teses/disponiveis/59/59138/tde-14092017-164746/publico/Dissertacao.pdf . Acesso em: 20 jan. 2020.
VAN VLACK, L. H. Princípios de ciência e tecnologia dos materiais. Rio de Janeiro: Elsevier, 1984.