Caro aluno, existem vários exemplos de elementos carregados axialmente, como membros de suporte, hastes de conexão em motores, aros em rodas de bicicleta, colunas em prédios, elementos como molas, cabos e barras prismáticas.

O grande problema de elementos carregados axialmente é a determinação de sua deformação, como o alongamento, encurtamento e deslocamento causado pelos carregamentos axiais.

Nesse sentido, suponha que um elemento carregado axialmente tem o efeito de diminuir em seções mais afastadas das extremidades, conforme a Figura 2.1.

Como podemos observar, as deformações se nivelam e tornam-se uniformes em toda a seção média da barra. A tensão no interior da barra será distribuída uniformemente por toda a área da seção transversal (afastado do ponto de aplicação da carga externa). A seção a-a, próxima da extremidade e do carregamento, possui flechas que indicam vetores de força de intensidade média que, por sua vez, são distribuídas de forma não uniforme. A seção b-b, mais afastada da extremidade que a seção a-a, mostra uma diminuição na intensidade média das flechas e a discrepância na distribuição de intensidades é menor do que em a-a. Já a seção c-c, mais afastada da extremidade do que  a seção b-b, tem um perfil de distribuição de intensidades uniforme.

A distância mínima entre a extremidade e dita seção transversal é igual à maior dimensão da seção transversal carregada, isso não é regra geral.

Princípio de Saint-Venant

O Princípio de Saint-Venant afirma que:

• Efeitos localizados ou causados por cargas que agem no corpo são dissipados em regiões, suficientemente, afastadas do ponto de aplicação;
• A tensão e a deformação produzidas em pontos de um corpo suficientemente distantes da região de aplicação de carga e de vínculos serão iguais às tensões e deformações produzidas por qualquer carregamento aplicado, que possua a mesma resultante estaticamente equivalente e sejam aplicados ao corpo dentro da mesma região.

Molas Submetidas a Cargas Axiais

A mola submetida a carregamentos axiais é analisada observando os seguintes princípios:

• É feita de um material elástico linear;
• O material resiste à tração e compressão;
• A constante de rigidez k , que é definida como a força necessária para produzir uma unidade de alongamento;
• f é a flexibilidade (também chamada de compliância) definida como o alongamento produzido por uma carga unitária.

Dessa forma, temos as seguintes equações, eq. 1.1 de força necessária aplicada a uma mola para alongá-la a um valor \(\delta \), eq. 1.2 de uma deformação causada por uma força P e eq. 1.3 que resulta na rigidez de uma mola.

\(P~=~k\delta \) (eq. 1.1)   \(\delta ~=~fP\)(eq. 1.2)     \(k~=\frac{1}{f}\)(eq. 1.3)

Cabos Sujeitos a Cargas Axiais

Cabos são utilizados para transmitir cargas de tração e não resistem à compressão. Além disso, eles têm pouca resistência à flexão. Um cabo é composto de um grande número de fios que são entrelaçados, a fim de obter configurações diferentes. A área transversal (ou efetiva) é menor que a área de um círculo com o mesmo diâmetro que o cabo, portanto, o módulo de Young também é menor do que o material do qual ele é feito.

Barras Prismáticas Sujeitas a Cargas Axiais

Por sua vez, barras prismáticas são elementos estruturais como eixos longitudinais retilíneos com uma seção transversal que seja constante ao longo de seu comprimento e resistem tanto à tração quanto à compressão. As seções transversais possuem diversos tipos diferentes de geometrias, podendo ser ou não vazadas, com seções circulares e retangulares em I.

Nas barras prismáticas, uma carga denominada P age no centroide da seção. Logo, aplicando o conceito da tensão média (\({{\sigma }_{m\acute{e}d}}\)), temos que a força P age sobre uma área A , conforme eq. 1.4. Como o material é homogêneo, podemos aplicar o conceito da deformação média, conforme a eq. 1.5, em que \(\delta \) é o alongamento e \({{\varepsilon }_{m\acute{e}d}}\) é a deformação média. E, como o material é elástico linear, aplicamos a lei de Hooke, que relaciona a tensão com a deformação e o módulo de elasticidade, observe na figura eq. 1.6.

\({{\sigma }_{m\acute{e}d}}~=~\frac{P}{A}\)(eq. 1.4)    \({{\varepsilon }_{m\acute{e}d}}~=~\frac{\delta }{L}\)(eq. 1.5)  \({{\sigma }_{m\acute{e}d}}=E{{\varepsilon }_{m\acute{e}d}}\)(eq. 1.6)

A determinação da deformação elástica de uma barra carregada axialmente é calculada utilizando o seguinte conceito:

\[\delta =~\frac{PL}{AE}\]

Nesse sentido, existem  4 casos de barras prismáticos carregadas axialmente:

• Variações contínuas de cargas e dimensões;
• Seção transversal e força externas constantes;
• Carregamento axial em ponto intermediário;
• Segmentos prismáticos.

Convenção de sinais: P e δ são positivos em casos de tração e alongamento, eles são negativos apenas em casos de compressão e contração.

1.4.1 Procedimento de análise

O deslocamento relativo entre dois pontos, A e B, em um componente sujeito a uma carga axial pode ser determinado com uso do princípio de Saint-Venant e a Lei de Hooke, conforme a equação a seguir.

\[\delta =~\frac{PL}{AE}\]

• Determinação da força axial interna: método das seções para determinar a força interna P(x) em relação a uma extremidade e esboço do diagrama de força normal.
• Determinar o deslocamento relativo : especificar a força interna P(x) e o módulo elástico, em cada segmento; atribuir o sinal para P(x) conforme a convenção; calcular as deformações, da extremidade A em relação à B e do ponto A em relação ao ponto fixo B.

Exemplo 1

Uma barra de aço feita de aço A-36 é composta por dois segmentos, AB e BD, com áreas de seção transversal AB = 600 mm² e BD = 1200 mm². Nesse caso, precisamos determinar o deslocamento vertical da extremidade A e o deslocamento de B em relação a C.

Este caso, se trata de segmentos prismáticos, com vários segmentos, carga axial variável e áreas de seção transversal variáveis. O material é homogêneo, com E = 210 GPa.

As cargas internas são calculadas utilizando o método das seções e as equações de equilíbrio.

1. Deslocamento vertical da extremidade A (deslocamento de A em relação ao apoio fixo D).
   
   \({{\delta }_{A}}={{\delta }_{A/D}}=\underset{i=1}{\overset{3}{\mathop \sum }}\,{{\delta }_{i}}={{\delta }_{1}}+{{\delta }_{2}}+{{\delta }_{3}}\)
   
   \({{\delta }_{A}}=\underset{i=1}{\overset{3}{\mathop \sum }}\,\frac{{{P}_{i}}{{L}_{i}}_{{}}}{{{A}_{i}}E}=\frac{1}{E}\left( \frac{{{P}_{AB}}{{L}_{AB}}_{{}}}{{{A}_{AB}}}+\frac{{{P}_{BC}}{{L}_{BC}}_{{}}}{{{A}_{BC}}}+\frac{{{P}_{CD}}{{L}_{CD}}_{{}}}{{{A}_{CD}}} \right)\)
   
   \({{\delta }_{A}}=~+0,6101~mm\)
   ‍
2. Deslocamento da extremidade B em relação a C.
   
   \({{\delta }_{B/C}}={{\delta }_{2}}\)
   
   \({{\delta }_{B/C}}=\frac{{{P}_{BC}}{{L}_{BC}}_{{}}}{{{A}_{BC}}}\)= +0,1042 mm

Deformações Elásticas, Inelásticas e Térmicas

As Deformações Elásticas

Essas deformações são regidas pela Lei de Hooke, no regime elástico. Um exemplo de deformação elástica é aquele que ocorre em uma mola, que quando sujeita à uma força F, ela sofre deformação. Porém, quando a força F é removida, a mola volta a sua posição inicial.

As Deformações Inelásticas ou Plásticas

São aquelas em que não há capacidade de recuperação ao estado geométrico inicial. Suponha que um cilindro é sujeito a uma força compressiva axial F . O cilindro sofre deformações que vão além da deformação na direção da força de compressão. Nesses casos, a lei de Hooke não se aplica.

As Deformações Térmicas

Elas ocorrem quando uma mudança na temperatura provoca alterações nas dimensões do material. O aumento de temperatura tende a gerar uma expansão do material e uma diminuição tende a gerar uma contração no corpo. Considerando um material homogêneo e isotrópico, podemos calcular a deformação de um elemento com comprimento L por meio da fórmula a seguir.

\[{{\delta }_{T}}=\alpha \Delta TL\]

Em que, α é o coeficiente linear de expansão térmica, intrínseco ao material, ∆T é a variação de temperatura do elemento e L é o comprimento inicial do elemento.

A Torção é o efeito de rotação que o eixo longitudinal de uma peça sofre quando ela é solicitada por momentos/torques.

Torque ( T ) é o momento de rotação de um determinado corpo em torno de seu eixo longitudinal. O sentido do momento de torção é indicado pela regra da mão direita .

A torção pura é o tipo de torção que ocorre em peças que apresentam seção transversal idêntica ao longo de todo o seu eixo longitudinal, que são sujeitas ao mesmo torque interno. Nesse material, abordaremos casos de torção pura.

Considerando um elemento longo com seção transversal circular, como um eixo, é importante o estudo do efeito do torque nesse tipo de componente, pois ele tem aplicação em muitos mecanismos dentro da engenharia.

Se aplicarmos um torque na extremidade de um eixo que esteja preso na sua outra extremidade, como mostrado na figura a seguir, obteremos um ângulo formado entre uma linha radial localizada em uma seção transversal do eixo, antes e depois da deformação gerada pelo torque. Esse ângulo é denominado ângulo de torção ϕ, veja na Figura 2.6, ele variará ao longo do comprimento x do eixo.

Nesse sentido, é importante ressaltar que quando o ângulo de rotação entre as extremidades da barra é pequeno, o comprimento da barra e o raio da seção transversal permanecem inalterados, mesmo depois da deformação.

Se analisarmos somente um elemento isolado da barra da Figura 2.7 sendo torcido, veremos que devido a diferença de deformações entre a face anterior e posterior do elemento, ele ficará em cisalhamento puro.

A deformação por cisalhamento ( γ ) no interior do eixo varia de forma linear ao longo de qualquer linha radial, de zero na linha central do eixo até um valor máximo ( γ máx) em seu contorno externo . A deformação por cisalhamento em qualquer ponto da linha radial (ρ) pode ser obtida por meio da equação:

\[\gamma =\left( \frac{\rho }{c} \right){{\gamma }_{m\acute{a}x}}\]

Obs.: essa fórmula só pode ser utilizada em tubos circulares.

Fórmula de Torção

Quando um torque externo é aplicado a um eixo, ele cria um torque interno correspondente no interior do eixo.

Se o material for linear elástico, homogêneo, então a lei de Hooke será aplicada.

\[\tau =G\gamma \]

Por consequência, podemos afirmar que a variação linear na deformação por cisalhamento resulta em uma variação linear na tensão de cisalhamento correspondente ao longo de qualquer linha radial na seção transversal.

Assim, conforme mencionado anteriormente para a deformação por cisalhamento ( γ) , a tensão de cisalhamento (τ) variará de zero na linha central do eixo até um valor máximo (τmáx) na superfície externa. Para obtermos o valor da tensão de cisalhamento em qualquer ponto da linha radial (ρ), precisamos calcular:

\[\gamma =\left( \frac{\rho }{c} \right){{\gamma }_{m\acute{a}x}}\]

Cada elemento de área (dA), localizado em ρ, está sujeito a uma força de cisalhamento:

\[{{F}_{\tau }}=\tau dA\]

Podemos obter o momento de cisalhamento calculando a seguir equação:

\[{{M}_{\tau }}=\rho {{F}_{\tau }}=\rho \tau dA=\rho \left( \frac{\rho }{c} \right){{\tau }_{m\acute{a}x}}dA=\left( \frac{{{\tau }_{m\acute{a}x}}}{c} \right)\rho {}^\text{2}dA\]

Já o torque interno resultante ( T ) agindo na seção transversal é obtido por:

\[T=\underset{A}{\overset{{}}{\mathop \int }}\,{{M}_{\tau }}={{\left( \frac{{{\tau }_{m\acute{a}x}}}{c} \right)}_{{}}}\underset{A}{\overset{{}}{\mathop \int }}\,\rho {}^\text{2}dA\]

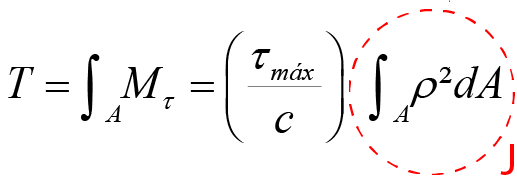
Logo, a integral destacada e identificada de J é conhecida como momento polar de inércia da seção transversal do eixo e depende somente da geometria do eixo. Com isso, a fórmula da tensão máxima de cisalhamento pode ser representada como a fórmula de torção.

\[{{\tau }_{m\acute{a}x}}=\frac{Tc}{J}\]

A tensão de cisalhamento para um ponto intermediário da linha radial (ρ) pode ser calculada por:

\[{{\tau }_{m\acute{a}x}}=\frac{Tc}{J}\]

Assim, a tensão de cisalhamento para um ponto intermediário da linha radial (ρ), por sua vez,  pode ser calculada por:

\[\tau =\frac{T\rho }{J}\]

• Nesse sentido, a Tensão máxima de cisalhamento do eixo, na superfície externa é obtida em Pa (N/m²);
• A Tensão de cisalhamento em um ponto intermediário da linha radial é obtida em (N/m²);
• O Torque interno resultante na seção transversal é obtido em N.m;
• O Raio externo do eixo é dado é obtido em m;
• O Raio intermediário do eixo é obtido em m ;
• O Momento polar de inércia é obtido em m⁴.

Para um eixo circular sólido, J é calculado por meio da igualdade a seguir.

\[J=\frac{\pi }{2}{{c}^{4}}\]

Já para um eixo circular tubular J é obtido pelo cálculo de:

\[J=\frac{\pi }{2}\left( c_{ext}^{4}-c_{int}^{4} \right)\]

Sendo “ c ext ” o raio externo do tubo e “ c int ” o raio interno do tubo. Ressaltamos que,  estas fórmulas de torção só devem ser utilizadas se o eixo for circular e o material se comportar conforme a lei de Hooke.

Diagrama de Torque

Nessa seção, encontraremos aplicações em que diferentes torques serão aplicados ao longo do comprimento de um eixo. A tensão de cisalhamento máxima neste eixo ocorrerá na região onde o maior torque agir. Para determinar essa região de maior torque, devemos montar o diagrama de torque .

Para se conseguir somar diferentes torques aplicados ao longo de um eixo, é necessário que haja uma convenção em seus sinais. Para isso, usamos a regra da mão direita, pela qual o torque e o ângulo serão positivos se a direção indicada pelo polegar for no sentido para fora ou se afastando da seção do eixo considerada, conforme mostrado anteriormente.

Exemplo 2

Observe o caso a seguir, em que quatro torques estão agindo sobre o eixo.

Para definir o torque de cada um dos trechos (LAB, LBC e LCD), usaremos o método das seções .

Logo,

\[{{T}_{A}}-{{T}_{AB}}=0\]

\[{{T}_{AB}}={{T}_{A}}=80~N.m\]

\[{{T}_{A}}-{{T}_{B}}+{{T}_{BC}}=0\]

\[80-150+{{T}_{BC}}=0\]

\[{{T}_{BC}}=70~N.m\]

\[{{T}_{D}}-{{T}_{CD}}=0\]

\[{{T}_{CD}}={{T}_{D}}=10~N.m\]

Obs.: O sentido de giro de TAB, TBC e TCD são atribuídos durante o cálculo, se o resultado for negativo isso indica que foi atribuído o sentido oposto ao real.

Outra forma de calcularmos os valores dos torques em cada região do eixo é montando o diagrama de torque , conforme figura a seguir.

Podemos notar que a região com maior torque está entre A e B, com T=80 N.m, logo, é nessa região onde teremos a tensão máxima de cisalhamento. Supondo que, o eixo seja maciço e tenha diâmetro de 30 mm, ou seja, raio de 15 mm, o momento polar de inércia pode ser obtido através do cálculo a seguir.

\(J=\frac{\pi }{2}{{c}^{4}}=\frac{\pi }{2}{{0,015}^{4}}=79,52\times {{10}^{-9}}{{m}^{4}}\)

E, a tensão máxima de cisalhamento no eixo será:

\({{\tau }_{m\acute{a}x,AB}}=\frac{{{T}_{AB}}c}{J}=\frac{80\times 0,015}{79,52\times {{10}^{-9}}}=15\times {{10}^{6}}Pa=~15~MPa\)

Transmissão de Potência

Na maioria das vezes, em uma transmissão de potência gerada por uma máquina, os eixos circulares serão aplicados. Dessa forma, o torque desenvolvido no eixo pela máquina depende diretamente da potência do motor. A relação entre potência e torque é dada pela equação:

\[P=T\omega \]

• ω representa a velocidade angular do eixo, dada em rad/s;
• P é a potência do motor dada em W (watts).

Outra importante relação é a de frequência de rotação do eixo (f), que pode ser expressada por meio da igualdade:

\[P=2\pi fT\]

• em que, f é a frequência de rotação do eixo, dada em ciclos/s ou Hz (Hertz);
• Lembrando que: 1 ciclo equivale a 2π rad;

Com isso, durante o projeto de um eixo, em caso de obtermos apenas algumas informações disponíveis como a potência do motor, a frequência de rotação e a tensão de cisalhamento admissível do material, podemos utilizar as fórmulas apresentadas para se obter o torque T desenvolvido, e assim determinar a dimensão do eixo conforme a necessidade.

Por exemplo, no caso de um eixo maciço, o raio do eixo pode ser determinado variando “c” até o valor da tensão de cisalhamento obtido seja menor que a tensão admissível do material. Para isso, utilize a seguir fórmula.

\[{{\tau }_{m\acute{a}x}}=\frac{Tc}{J}=\frac{Tc}{\left( \frac{\pi }{2}{{c}^{4}} \right)}\]

Ângulo de Torção

Em algumas aplicações, é necessário calcular o ângulo de torção ϕ, mencionado anteriormente, que é o ângulo formado entre uma extremidade de um eixo em relação a outra após a torção.

Considerando um eixo de material homogêneo, como módulo de elasticidade de cisalhamento (G) constante e área da seção transversal constante ao longo seu comprimento, a relação entre o torque aplicado e o ângulo de torção poder ser obtida por meio da igualdade a seguir.

\[\Phi =\frac{TL}{JG}\]

Em que:

• ϕ é o Ângulo de torção em radianos ( rad );
• T é o Torque interno determinado pelo método das seções, dado em N.m;
• L é o Comprimento do trecho do eixo analisado em m ;
• J é o Momento polar de inércia mm4.
• G é o Módulo de elasticidade ao cisalhamento do material em Pa.

Uma haste de roupeiro segura diversos cabides e cada cabide carrega consigo casacos, camisas, etc. A haste está sujeita um tipo de carregamento, ou seja, a haste pode ser considerada um elemento estrutural do roupeiro, pois tem a função de manter as roupas no seu devido lugar.

Nesse sentido, podemos transpor esse conceito para nosso contexto, quando uma viga é sujeita a um sistema de carregamentos ou força que age perpendicularmente ao eixo de simetria longitudinal, ela deformará. Em termos simples, a deformação que ocorre nesse sentido é chamada de flexão de uma viga. Devido à força de cisalhamento e ao momento fletor, a viga sofre deformação.

Para calcular a tensão de flexão de uma viga, considere os pontos listados a seguir.

• Inicialmente, a viga é reta e tem seção transversal constante;
• A viga é feita de um material homogêneo e tem um plano longitudinal de simetria;
• A resultante de cargas aplicadas fica no plano de simetria;
• A geometria do membro como um todo, em que a causa de falha é flexão e não flambagem;
• O limite elástico não é excedido e E é o mesmo em tensão e compressão;
• O plano da seção transversal permanece plano antes e depois da flexão.

A flexão é pura quando ocorre apenas por causa dos vínculos nas extremidades. Neste caso, não existe chances de tensão de cisalhamento na viga. A tensão que se propaga na viga é uma tensão normal, não ocasionando danos à viga.

Por outro lado, a flexão será simples quando ela acontecer por causa do próprio peso da viga e/ou um carregamento externo. Nesse caso, ela resulta em tensão de cisalhamento e tensão normal na viga.

\[\frac{M}{I}=\frac{\sigma }{y}=\frac{E}{R}\]

Em que M é o momento fletor, I é o momento de inércia da seção do eixo de flexão, R é o raio de curvatura da viga fletida e y é a distância perpendicular ao eixo neutro.

Diagramas de Força Cortante e Momento Fletor

Os diagramas de força cortante e momento fletor são ferramentas analíticas usadas na análise estrutural, com o objetivo de obter a noção dos pontos críticos em um elemento estrutural, como uma viga. Eles fornecem informações que determinam o tipo, o tamanho e o material que um membro estrutural deve possuir para suportar os carregamentos sem falhas.

Se a variação da força cortante V e do momento fletor M são escritos como funções de posição ( x ), e plotados, obtemos os diagramas de força cortante e momento fletor.

A inclinação do diagrama de força cortante corresponde a negativa do carregamento distribuído. A inclinação do diagrama de momento é o cisalhamento. A área negativa sob o diagrama de carregamento representa a mudança da força cortante e a área sob o diagrama de força cortante representa a mudança no momento fletor.

A seguir, veja um exemplo do procedimento de análise adotado para os diagramas de força cortante e momento fletor, considerando a viga.

• 1º passo: encontrar as reações de apoio. Para esse passo, utilize as seguintes igualdades:

\[\underset{{}}{\overset{{}}{\mathop \sum }}\,{{M}_{A}}=0=-P\left( L+2L \right)+{{B}_{y}}\left( 3L \right)\]

\[\underset{{}}{\overset{{}}{\mathop \sum }}\,{{F}_{Y}}=0={{A}_{y}}+{{B}_{y}}-2P\]

\[{{A}_{y}}={{B}_{y}}=P\]

\[\underset{{}}{\overset{{}}{\mathop \sum }}\,{{F}_{x}}=0={{A}_{x}}\]

• 2º passo: estabelecer os eixos V e x e plotar os valores de força cortante em cada extremidade. (x=0;V=P) e (X=3L;V=-P)
• No intervalo de 0 < x < L, a inclinação do diagrama é igual ao carregamento, que é w(x)=0. Portanto, obtemos uma linha reta.
• No ponto x = L, uma carga concentrada P de sinal negativo é aplicada. Há uma descontinuidade no diagrama e a cortante é 0.
• De L < x < 2L, w(x)=0 portanto a inclinação é nula também.
• Em 2L, há outra descontinuidade no diagrama, devido a aplicação da outra força P, também negativa. De 2L a 3L w(x)=0, portanto, a inclinação é nula.
• Em 3L, com a reação em B, o diagrama termina em 0.

Para o diagrama de momento fletor, considere os pontos listados a seguir.

• Estabeleça os eixos de M e x e as extremidades (x=0; M=0) e (x=3L; M=0);
• A inclinação de 0 < x < L é igual ao valor da cortante, nesse caso, V = P , indicando a inclinação positiva.
• A inclinação do momento de L < x < 2L é igual ao valor da cortante, nesse caso V = 0.
• A inclinação do momento de 2L < x < 3L é igual a V = - P.

Nesse sentido, podemos afirmar que, se um carregamento é dado por \(w\left( x \right)\), a inclinação de seu diagrama de força cortante será \(\frac{dV}{dx}=w\)e a inclinação de seu diagrama de momento fletor poderá ser obtida por \(\frac{dM}{dx}=V\).

Flexão Assimétrica

Em determinados casos, podemos encontrar carregamentos em que o momento interno não atue diretamente em torno dos eixos principais da seção transversal, mas em uma posição oblíqua em relação aos eixos. Na figura a seguir, um momento M é aplicado, formando um ângulo θ com o eixo principal z.

Neste caso, uma decomposição do momento oblíquo deve ser realizada para os eixos principais, de forma que a tensão gerada em um ponto (A, por exemplo) pela componente decomposta poderá ser calculada pela fórmula da flexão a seguir.

\[{{M}_{z}}=Mcos\theta \]

\[{{M}_{y}}=Msen\theta \]

\[\sigma {{A}_{z}}=-\frac{{{M}_{z}}{{c}_{y}}}{{{I}_{z}}}\]

\[\sigma {{A}_{y}}=\frac{{{M}_{y}}{{c}_{z}}}{{{I}_{y}}}\]

Logo, Iz e Iy correspondem aos momentos de inércia de área da seção transversal, dados em m⁴, mm⁴, etc.

Obs .: O sinal de negativo em σAz ocorre devido ao ponto A que é comprimido pelo Mz , ou seja, a sua tensão está no sentido negativo do eixo x estabelecido. Nesse sentido, podemos conferir, aplicando a regra da mão direita com o polegar apontando para a direção de Mz, notando que o restante dos dedos comprimem A. Se o ponto A estivesse abaixo do eixo z, ele seria tracionado por Mz , dessa forma, a tensão teria sinal positivo, como em σAz .

Por fim, utilizando a equação para determinação de tensões em uma flexão assimétrica, obtemos a tensão resultante para o ponto escolhido.

\[{{\sigma }_{A}}=-\frac{{{M}_{z}}{{c}_{y}}}{{{I}_{z}}}+{{\frac{{{M}_{y}}{{c}_{z}}}{{{I}_{y}}}}_{{}}}\]

A seguir, apresentamos uma representação gráfica da distribuição de tensões do caso analisado.

No exemplo, notamos que a linha neutra N do carregamento, ou seja, a linha em que as tensões são nulas. Nesse sentido, podemos ressaltar que o ângulo α não é o mesmo ângulo θ que o momento inicial M faz com o eixo z. O ângulo α pode ser determinado pela igualdade:

\[tg\alpha =\frac{{{I}_{z}}}{{{I}_{y}}}tg\theta \]