Resistência dos Materiais
Projeto de Vigas e Eixos, Deflexão e Flambagem em Colunas
Prezado(a) aluno(a), esta unidade é uma conclusão dos principais tópicos de Resistência dos Materiais e nela veremos tópicos que culminam em diversos assuntos que você já tem conhecimento. Aqui, a aplicação no projeto de eixos e vigas retoma diversos conceitos básicos para que o estudante possa, futuramente, planejar, analisar e projetar elementos estruturais solicitados por cargas diversas. Também veremos nesta unidade os conceitos de deflexão e flambagem, que são de suma importância na mecânica dos sólidos. Com o conteúdo aqui abordado, você vai adquirir conhecimento o suficiente para tornar-se autônomo na resolução de problemas, além de revisar tópicos de forma mais aplicada, e assim fixá-los.
O projeto de vigas e eixos tem como objetivo fazer vigas que resistam tanto ao cisalhamento quanto à flexão. Neste capítulo, vamos desenvolver métodos usados no projeto de vigas prismáticas e determinar a forma de vigas sujeitas à tensão, bem como o projeto de eixos sujeitos aos momentos fletores e torçores.
Primeiro, vamos contextualizar e fazer algumas considerações sobre vigas. O conceito de viga é bastante simples e compreende elementos estruturais que precisam suportar cargas perpendiculares ao seu eixo longitudinal (comprimento). Quando carregadas, existem a força interna de cisalhamento e o momento fletor que variam ao longo do eixo da viga, sendo que a tensão axial é negligenciada em projeto de vigas, uma vez que ela é muito mais baixa que o cisalhamento e o momento fletor. Para o projeto de vigas, utilizamos os conceitos de cisalhamento e flexão já conhecidos, apenas se a viga for homogênea e estiver no regime elástico linear.
A tensão de flexão e a tensão de cisalhamento não podem exceder a tensão admissível que são especificadas para a viga. Assim, vamos determinar o módulo de resistência à flexão da viga , dado por S :
\({{S}_{req}}=\frac{{{M}_{m\acute{a}x}}}{{{\sigma }_{adm}}}=\frac{I}{c}\) (eq. 4.1)
Onde \(M_{máx}\) é o momento fletor máximo, \({{\sigma }_{adm}}\) é a tensão admissível da viga, I é o momento de inércia da viga e c é a distância do eixo neutro até o ponto mais distante da seção transversal.
Conhecendo \({{S}_{req}}\), podemos determinar as dimensões da seção transversal da viga.
Opta-se por vigas de seção simétrica, caso a tensão de flexão admissível seja igual para tração e compressão. Caso contrário, opta-se por uma seção transversal assimétrica, que irá resistir aos diferentes momentos.
Desde que a viga satisfaça a equação de \({{S}_{req}}\), considera-se adequada para a aplicação. Busca-se sempre obter vigas com a menor área transversal possível, desde que não haja restrições de deformações.
Devemos, então, confirmar a escolha da viga pela análise do cisalhamento:
\({{\tau }_{adm}}\ge \frac{VQ}{It}\) (eq. 4.2)
Normalmente, esse passo não apresenta grandes problemas. Exceções incluem vigas feitas de madeira, uma vez que esta tende a dividir seus grãos devido ao cisalhamento. Caso a viga seja curta e suporte altas cargas concentradas, a tensão de cisalhamento pode ser crucial na escolha da viga.
Escolhendo a seção da viga : as vigas produzidas geralmente saem de um processo metalúrgico de laminação à quente. Vigas produzidas por esse processo são padronizadas e tabuladas pelo Instituto Americano de Construção em Aço (AISC).
As vigas são tabeladas e divididas de acordo com a sua seção transversal. Encontra-se comumente vigas de abas largas, as quais são descritas pela sua altura e peso por unidade de comprimento. Por exemplo, W 460 x 68 vai ter uma altura próxima a 460 mm e peso de 68 kgf/m. Veja na Figura 4.1 como essa viga de abas largas é representada.
Além da altura e do peso por unidade de comprimento, a área da seção, o momento de inércia e outras propriedades podem ser encontradas em tabelas de vigas.
Há ainda as vigas de aço de seções compostas produzidas por métodos de união, que juntam duas ou mais partes para formar uma viga única. Normalmente, são unidas por meio de parafusos ou soldas.
As vigas de madeira são normalmente retangulares, devido ao processo de fabricação, que é facilitado. Geralmente encontram-se as vigas do tipo caixão e as vigas compostas de lâminas coladas (madeira laminada).
Na análise de vigas, duas ferramentas que serão muito utilizadas são os diagramas de momento e de cisalhamento, a fim de encontrar os valores máximos de cisalhamento e momento. Para vigas compostas, esses diagramas servem para identificar pontos acumuladores de tensão que exigem reforços.
Caso a viga seja longa, encontramos o módulo de resistência à flexão utilizando a fórmula da flexão pela equação 4.1 e, com a mesma, computamos a seção transversal, uma vez que a equação nos diz que \(S_{req}= I/c\). Se vigas de perfis laminados forem usadas, vários valores de \(S\) podem ser selecionados, a partir de tabelas. Escolhe-se a viga com a menor área da seção transversal, uma vez que isso implica no menor peso e em uma maior economia.
Se estamos falando de uma viga curta, com altas cargas e, principalmente, vigas feitas de madeira , analisa-se primeiro a resistência ao cisalhamento, para depois checar os requerimentos quanto à tensão de flexão admissível. Para isso, utiliza-se a equação 4.2, a fim de verificar se a tensão admissível não foi excedida.
Caso a viga tenha uma seção retangular maciça , a fórmula é alterada, como vemos na equação 4.3:
\({{\tau }_{adm}}\ge 1,5\left( \frac{{{V}_{m\acute{a}x}}}{A} \right)\) (eq. 4.3)
Já no caso de uma viga com seção de abas largas , podemos assumir que o cisalhamento é constante na área da seção transversal da alma da viga, que é determinada pelo produto da altura da viga pela espessura da alma. Temos, portanto, um cisalhamento admissível dado pela equação 4.4:
\({{\tau }_{adm}}\ge \frac{{{V}_{m\acute{a}x}}}{{{A}_{alma}}}\) (eq. 4.4)
A adequação de elementos de fixação (como parafusos e pregos) depende da tensão de cisalhamento que os elementos podem resistir. O espaçamento entre esses elementos é determinado pelo fluxo de cisalhamento permitido, que é dado na equação 4.5, que deve ser calculada em pontos da seção onde há elementos de fixação:
\({{q}_{adm}}=\frac{VQ}{I}\) (eq. 4.5)
Exemplo 1:
Considere a viga feita de madeira laminada, conforme a Figura 4.2. Ela está sujeita a uma carga de 12 kN/m. É necessário que ela possua uma razão altura/largura de 1,5. Determine, com base nisso, a menor largura.
Considerando que para a viga, a tensão de flexão admissível é \({{\sigma }_{adm}}=9~MPa\) e a tensão de cisalhamento admissível é \({{\tau }_{adm}}=0,6~MPa\), sendo seu peso desprezível.
1º passo : construir diagramas de força cortante e momento fletor, conforme vemos na Figura 4.3.
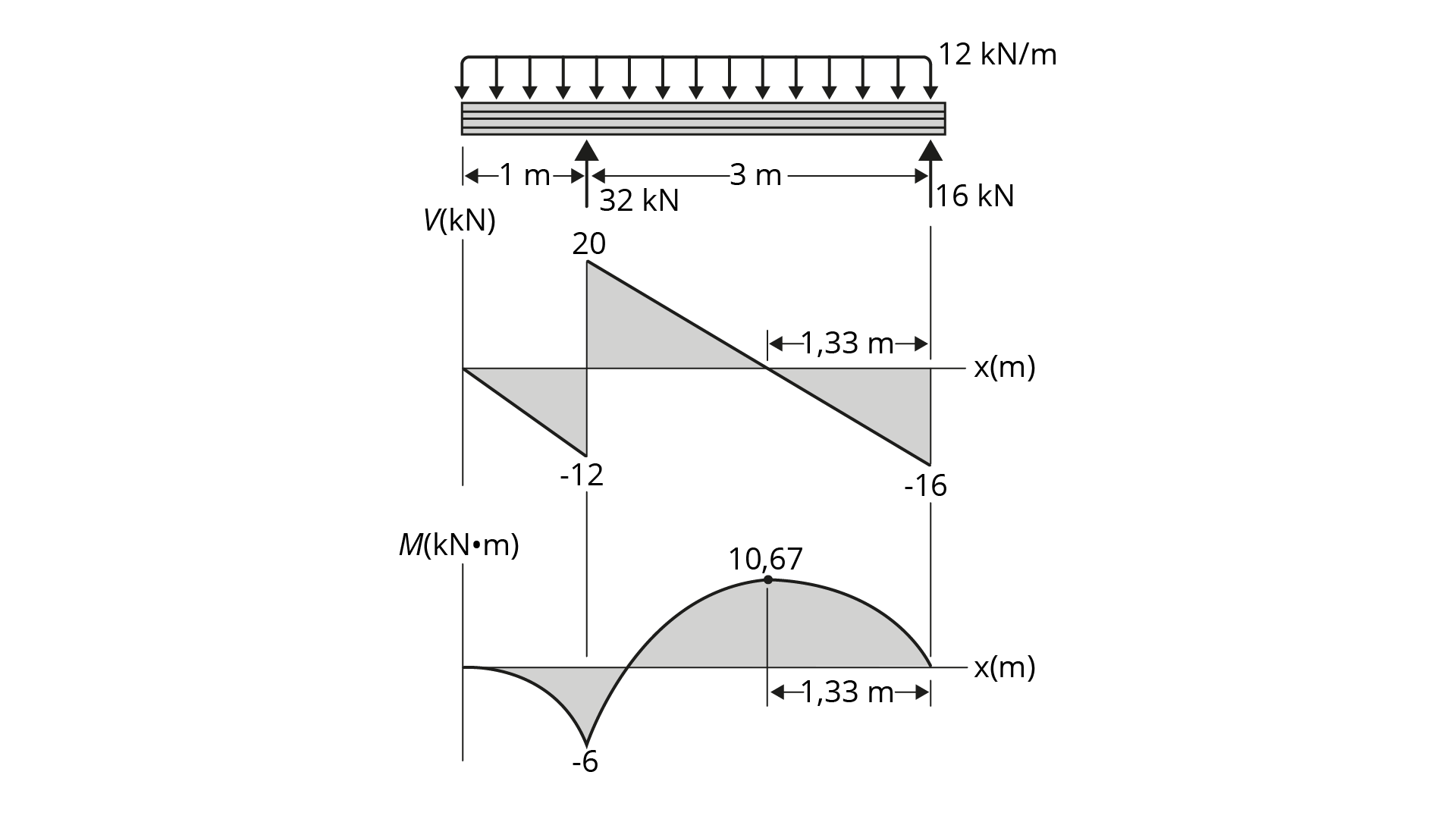
2º passo : Calcular o módulo de resistência à flexão e a largura:
\[{{S}_{req}}=\frac{{{M}_{m\acute{a}x}}}{{{\sigma }_{adm}}}=\frac{10,67\times {{10}^{6}}}{9}=1,19\times {{10}^{6}}mm{}^\text{3}\]
\[{{S}_{req}}=\frac{I}{c}=1,19\times {{10}^{6}}=\frac{\frac{1}{12}\left( a \right)\left( 1,5a \right){}^\text{3}}{\left( 0,75a \right)}\]
\[a{}^\text{3}=3,16\times {{10}^{6}}mm{}^\text{3}\]
\[a=147~mm\]
3º passo : Devemos lembrar que vigas de madeira precisam ser avaliadas em relação ao seu cisalhamento, portanto, calculamos o cisalhamento para seções retangulares, neste caso:
\[{{\tau }_{adm}}\ge 1,5\left( \frac{{{V}_{m\acute{a}x}}}{A} \right)=\left( 1,5 \right)\frac{20.000}{\left( 147 \right)\left( 1,5 \right)\left( 147 \right)}=0,93~>0,6~MPa\]
Podemos ver que com a largura projetada para flexão, ocorre falha por cisalhamento. Neste caso, devemos reprojetar a viga, de acordo com o critério de tensão de cisalhamento admissível.
\[{{\tau }_{adm}}=1,5\left( \frac{{{V}_{m\acute{a}x}}}{A} \right)\]
\[0,6=1,5\frac{20.000}{a\left( 1,5a \right)}\]
\[a=183~mm\]
Deste modo, a largura mínima para essa viga retangular de madeira laminada é de 183 mm.
O exemplo acima evidencia bem como vigas de madeira e, nesse caso, sujeita a uma carga distribuída ao longo de seu comprimento, pode falhar por cisalhamento e necessitar de reprojeto, para atender às propriedades do material.
Durante um projeto de viga, o engenheiro poderá optar por uma viga que economize peso. Para tal, utiliza-se vigas que possuem uma seção transversal variável, fazendo com que, em cada seção diferente, tensões de flexão atinjam seu valor máximo permitido. Essas vigas são chamadas de não prismáticas. A Figura 4.4 mostra dois exemplos de vigas não prismáticas.
De forma geral, o tamanho da seção transversal de tais vigas se dá pela fórmula. Vigas com esse design são chamadas de vigas totalmente solicitadas.
Eixos de seção transversal circular são amplamente utilizados em máquinas e demais equipamentos mecânicos. Esses elementos estão sujeitos a tensões cíclicas, que provêm de combinações de flexão e torção que eles devem transmitir, além de conterem concentradores de tensão como acoplamentos, polias, engrenagens, mudanças bruscas na área da seção etc.
Carregamentos em eixos podem ser resolvidos transformando-os em componentes estaticamente equivalentes e decompondo-os em dois planos perpendiculares. Isso implica no fato de que diagramas de momento podem ser desenhados para as cargas de cada plano e o resultante interno de momento em cada seção do eixo é determinado pela adição de vetores, como:
\(M=\sqrt{{{M}_{x}}^{2}+{{M}_{z}}^{2}}\) (eq. 4.6)
Além do momento, os eixos estão sujeitos a torques internos diferentes. Faz-se necessária também a construção do diagrama de torque. Com os diagramas, é possível analisar as condições críticas nas seções do eixo, onde a combinação de um momento M e um torque T cria a pior situação de tensão. Com isso, aplica-se a fórmula de flexão usando a resultante do momento no eixo principal de inércia.
Geralmente o elemento crítico está sujeito ao estado plano de tensões, assim sendo:
\(\sigma =\frac{Mc}{I}\) (eq. 4.7) e \(\tau =\frac{Tc}{J}\) (eq. 4.8)
Fazendo uso das equações de transformação de tensão, temos que:
\({{\tau }_{adm}}=\sqrt{\left( \frac{\sigma }{2} \right){}^\text{2}+\tau {}^\text{2}}=\sqrt{\left( \frac{Mc}{2I} \right){}^\text{2}+\left( \frac{Tc}{J} \right){}^\text{2}}\) (eq. 4.9)
E uma vez que \(I=\pi {{c}^{4}}/2\) e \(J=\pi {{c}^{4}}/2\), ficamos com:
\({{\tau }_{adm}}=\frac{2}{\pi c{}^\text{3}}\sqrt{M{}^\text{2}+T{}^\text{2}}\) (eq. 4.10)
Resolvendo para o raio do eixo, temos:
\(c={{\left( \frac{2}{\pi {{\tau }_{adm}}}\sqrt{M{}^\text{2}+T{}^\text{2}} \right)}^{1/3}}\) (eq 4.11)
Assim sendo, conhecendo a pior condição de tensão, a partir dos diagramas de momento fletor e torque, podemos obter o raio mínimo do eixo, para que ele possa suportar as cargas que são impostas.
Exemplo 2
Considere o eixo suportado por mancais radiais em A e B. Devido à transmissão de potência do e para o eixo, as correias e polias estão sujeitas a tensões, conforme a Figura 4.5(a). Determine o menor diâmetro para o eixo, utilizando a teoria de máxima tensão de cisalhamento, com \({{\tau }_{adm}}=50~MPa\)
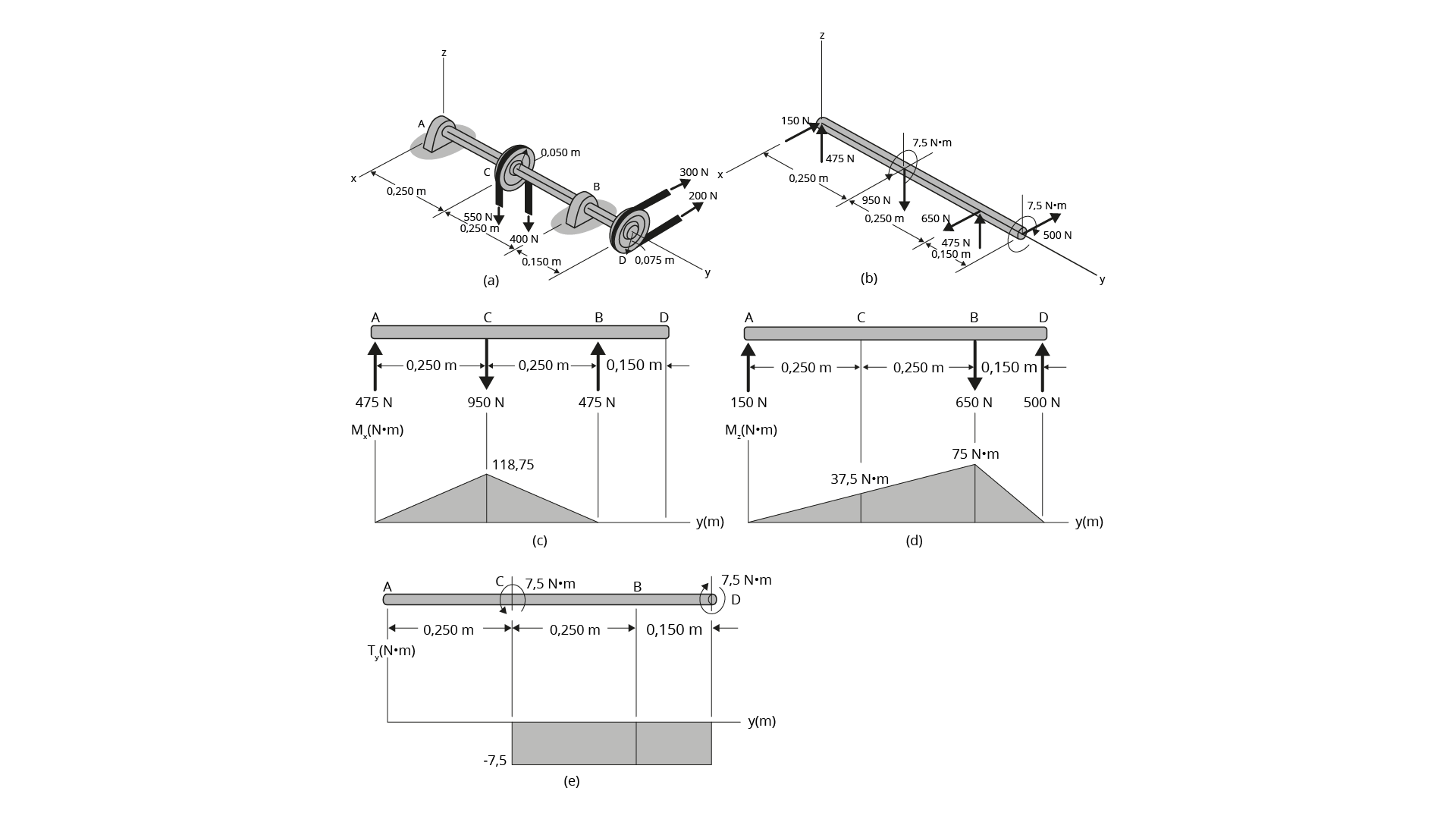
Por inspeção, os pontos críticos no diagrama de momento fletor ocorrem em B ou C. Também, à direita de C e no ponto B, o momento de torção é 7,5 N.m O momento resultante deve ser calculado para os dois pontos, portanto:
\[{{M}_{C}}=\sqrt{\left( 118,75~N.m \right){}^\text{2}+{{\left( 37,5~N.m \right)}_{{}}}^{2}}=124,5~N.m\]
\[{{M}_{B}}=\sqrt{\left( 75~N.m \right){}^\text{2}}=75~N.m\]
Assim, o ponto C contém os valores críticos para o projeto do eixo. Dessa forma, aplicamos a equação do raio do eixo para o caso.
\[c={{\left( \frac{2}{\pi {{\tau }_{adm}}}\sqrt{M{}^\text{2}+T{}^\text{2}} \right)}^{1/3}}=\left( \frac{2}{\pi \left( 50 \right)\left( {{10}^{6~}} \right)~}\sqrt{\left( 124,5 \right){}^\text{2}+\left( 7,5 \right){}^\text{2}} \right)_{{}}^{1/3}\]
\[c=0,0117~m\]
Como o exercício pede que se encontre o menor diâmetro, multiplicamos por 2 o raio do eixo. Assim, d = 2c =23,3 mm .
Dentro do contexto de vigas, devemos ter cuidado ao fazer as considerações sobre as solicitações e parâmetros de análise. Essas tarefas são imprescindíveis para um projetista e para tal, vamos exercitar alguns conceitos vistos neste capítulo da unidade, a fim de retomar alguns dos principais conceitos.
Vejamos as seguintes afirmações sobre o projeto de vigas. Leia-as atentamente e a seguir responda, baseado no conhecimento adquirido neste capítulo, quais afirmações são verdadeiras.
I - A falha da viga ocorre quando o cisalhamento interno ou o momento fletor na viga é máximo.
II - Para que a viga resista, a tensão máxima de cisalhamento e a tensão de flexão devem exceder valores de tensão admissível.
III - Deve-se primeiro verificar a tensão de cisalhamento da viga, para auxiliar na escolha da seção transversal.
IV - Um eixo mecânico deve resistir à torção e à flexão.
V - Para resolver o momento fletor de um eixo precisamos de dois diagramas, um para cada plano onde a carga é decomposta.
Em engenharia, deflexão é o grau de deslocamento de um elemento estrutural sob um carregamento, seja em ângulo ou em distância. A deflexão deve ser limitada, para prover estabilidade e evitar a propagação de trincas. Neste capítulo abordaremos métodos para computar deflexão em pontos específicos ao longo da viga ou a forma de deflexão de uma viga toda. Discutiremos o método de integração, que baseia-se na integração de equações diferenciais da linha elástica, o método da superposição e o método das áreas.
A linha elástica representa a linha de deflexão de um eixo ou viga. A linha elástica obrigatoriamente passa pelo centroide da seção transversal da viga. É relativamente fácil obter sua forma, porém alguns conceitos de estática precisam estar em mente, como, por exemplo, um suporte que resiste à força, tal como um pino, restringe deslocamento, e um suporte que resiste à momento, como um engaste, restringe rotação ou inclinação.
Para determinar sua forma, usa-se o diagrama de momento. Momentos positivos tornam-na côncava para cima e momentos negativos tornam-na côncava para baixo. O raio de curvatura (\(\rho\)), que é o raio de curvatura em um ponto específico sobre a linha elástica, é dado por:
\(\frac{1}{\rho }=\frac{M}{EI}\) (eq. 4.12)
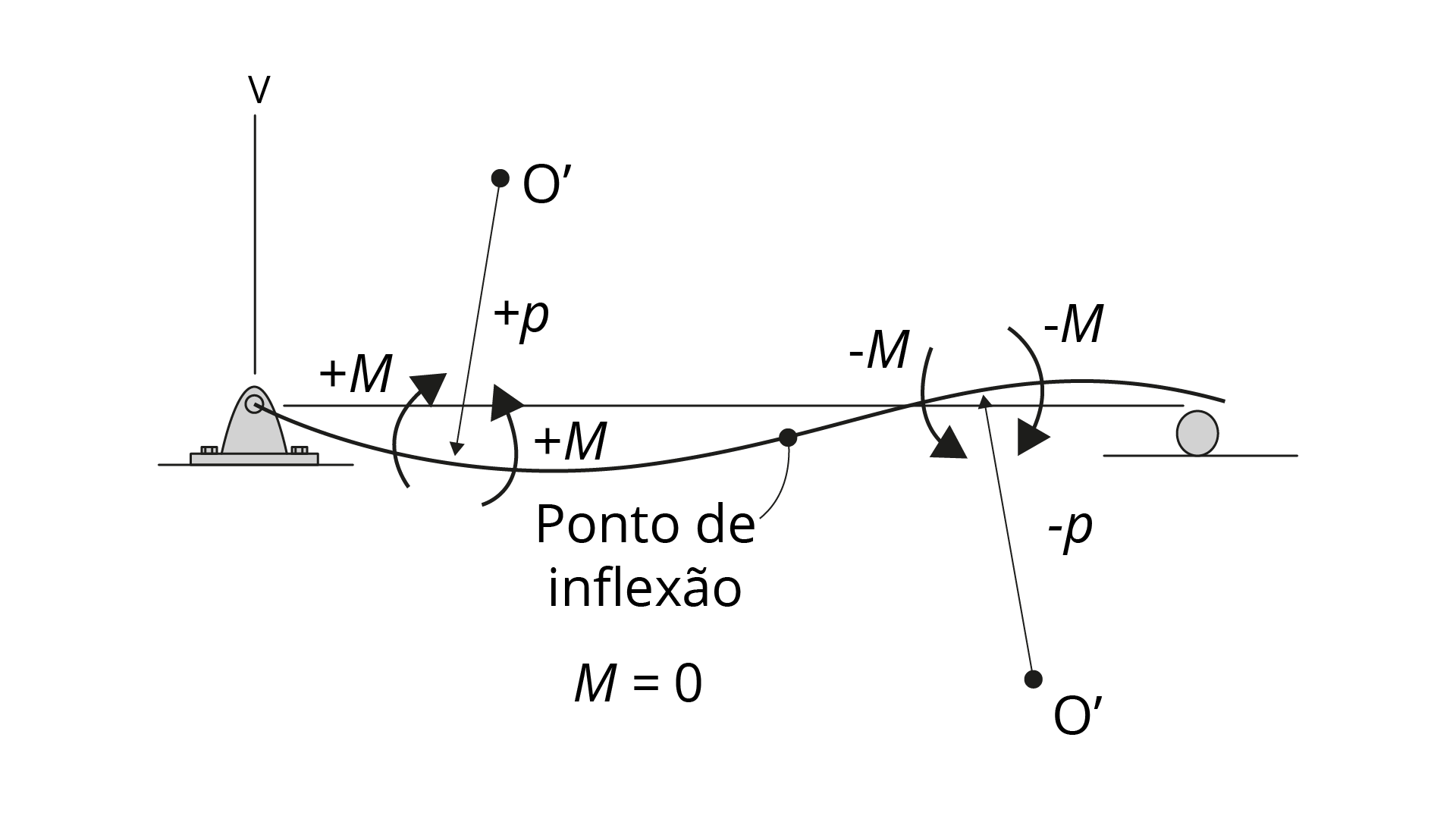
M é o momento interno no ponto onde quer se saber o raio, E o módulo elástico do material e I o momento de inércia em torno do eixo neutro. O deslocamento é representado por v .
As seguintes equações diferenciais são válidas no cálculo de deslocamento da linha elástica em uma viga.
\[EI\frac{d{}^\text{2}v}{dx{}^\text{2}}=M\left( x \right)\] (eq. 4.13) \[\frac{d}{dx}\left( EI\frac{d{}^\text{2}v}{dx{}^\text{2}} \right)=V\left( x \right)\] (eq. 4.14) \[\frac{d{}^\text{2}}{dx{}^\text{2}}\left( EI\frac{d{}^\text{2}v}{dx{}^\text{2}} \right)=-w\left( x \right)\] (eq. 4.15)
Essas equações nos dizem que uma função do momento M(x) , vista em 4.13, pode ser integrada para obter a equação da inclinação da linha elástica (4.14) e uma segunda integração nos retorna à equação da deflexão (4.15).
Para resolver um problema de linha elástica pelo método de integração, seguimos o seguinte roteiro:
Determine a deflexão máxima no eixo circular maciço. O eixo é feito de um aço com
E
= 200 GPa e
I
= 4,91 x 10\(^6\) mm\(^4\) (em metros,
I
= 4,91 x 10\(^{-6}\) m\(^4\)).
Inicialmente, encontramos as reações e traçamos um esboço da linha elástica, conforme vemos na Figura 4.8.
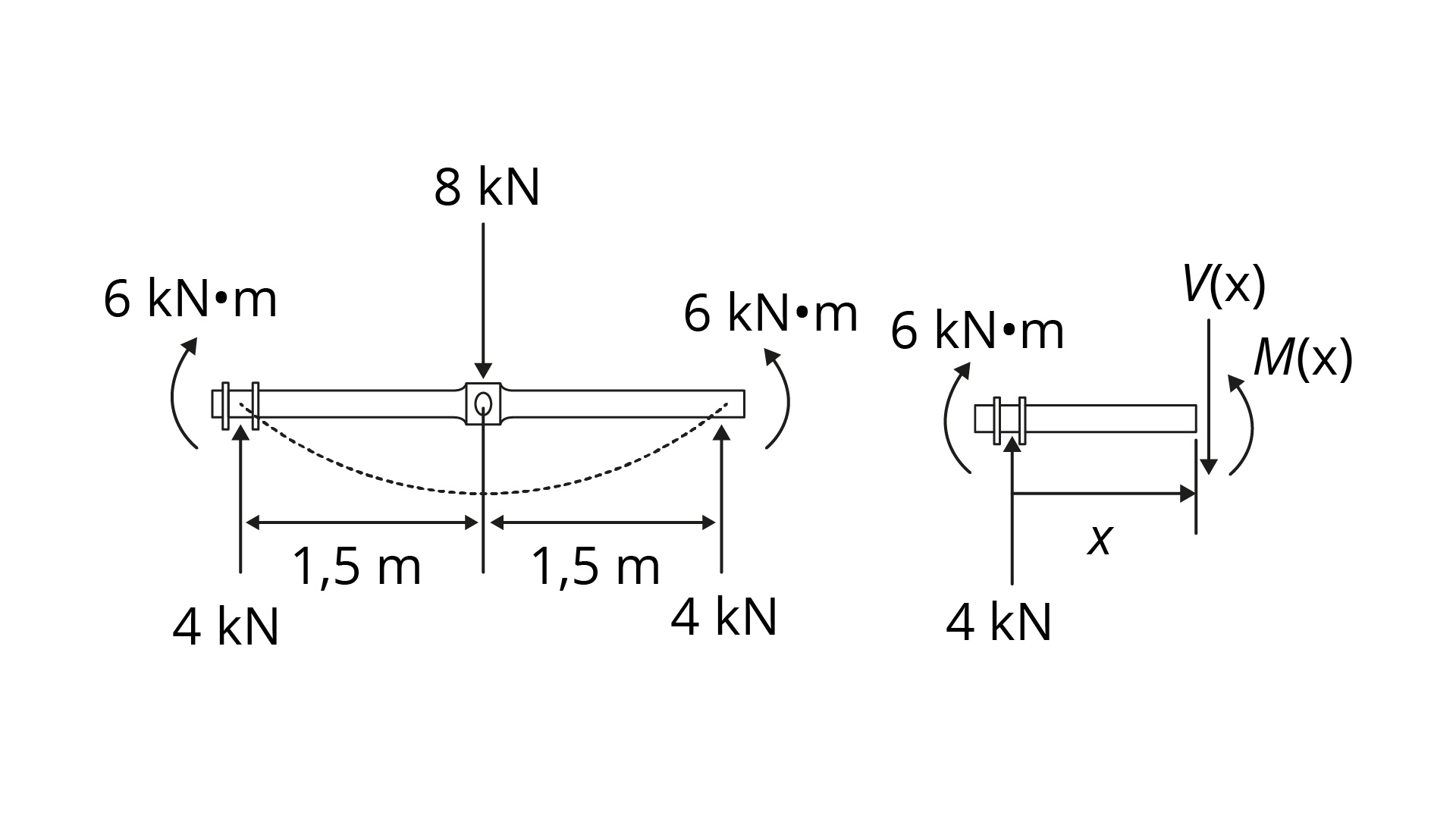
Com base no diagrama de corpo livre do segmento, encontramos as funções de momento. Devido a sua simetria, vamos analisar apenas as coordenadas x.
\[\mathop{\sum }_{{}}^{{}}{{M}_{O}}=0\] \[M\left( x \right)~-~4x~-~6~=~0\] \[M\left( x \right)~=~\left( 4x~+~6 \right)~kN.m\]
Com a função do momento, podemos encontrar as equações de inclinação e a linha elástica, integrando-a duas vezes:
\[EI\frac{d{}^\text{2}v}{dx{}^\text{2}}=M\left( x \right)=4x+6\] \[EI\frac{dv}{dx}=2x{}^\text{2}+6x+{{C}_{1}}\] \[EIv=\frac{2}{3}x{}^\text{3}+3x{}^\text{2}+{{C}_{1}}x+{{C}_{2}}\]
Devido à simetria, \(\frac{dv}{dx}=0\) no ponto x=1,5 m. Assim, temos:
\[EI\left( 0 \right)=2\left( 1,5 \right){}^\text{2}+6\left( 1,5 \right)+{{C}_{1}}\] \[{{C}_{1}}=-13,5~kN.m{}^\text{2}\]
Além disso, em x=0, v=0. Assim:
\[EI\left( 0 \right)=\frac{2}{3}\left( 0 \right){}^\text{3}+3\left( 0 \right){}^\text{2}+{{C}_{1}}\left( 0 \right)+{{C}_{2}}\] \[{{C}_{2}}=0\]
Substituindo os valores das constantes de integração, teremos:
\[v=\frac{1}{EI}\left( \frac{2}{3}x{}^\text{3}+3x{}^\text{2}-13,5x \right)\]
Como sabemos que a deflexão máxima ocorre em x = 1,5 m , onde a inclinação da linha elástica é nula , vamos ter que:
\[{{v}_{m\acute{a}x}}=\frac{1}{\left( 200\times {{10}^{9}} \right)\left( 4,91\times {{10}^{-6}} \right)}\left( \frac{2}{3}\left( 1,5 \right){}^\text{3}+3\left( 1,5 \right){}^\text{2}-13,5\left( 1,5 \right) \right)\times 10{}^\text{3}\]
\[{{v}_{m\acute{a}x}}=~-0,001146~m~=~11,5~mm~\downarrow\]
O método da superposição pode ser usado para resolver deslocamentos ou rotações em vigas ou carregamentos mais complicados; a viga estudada deve ser dividida em partes, as quais são casos mais simples e são disponibilizados em tabelas.
A equação diferencial \(EI{{d}^{4}}v/d{{x}^{4}}=-w\left( x \right)\) satisfaz os dois requisitos necessários para a aplicação do princípio da superposição: a carga w(x) está relacionada linearmente com a deflexão v(x) e w(x) não altera de forma significativa a geometria original da viga.
Veja o exemplo a seguir para melhor compreensão.
Exemplo 4
Determine o deslocamento em C e a inclinação do suporte A na viga vista na Figura 4.9. Considere EI constante.
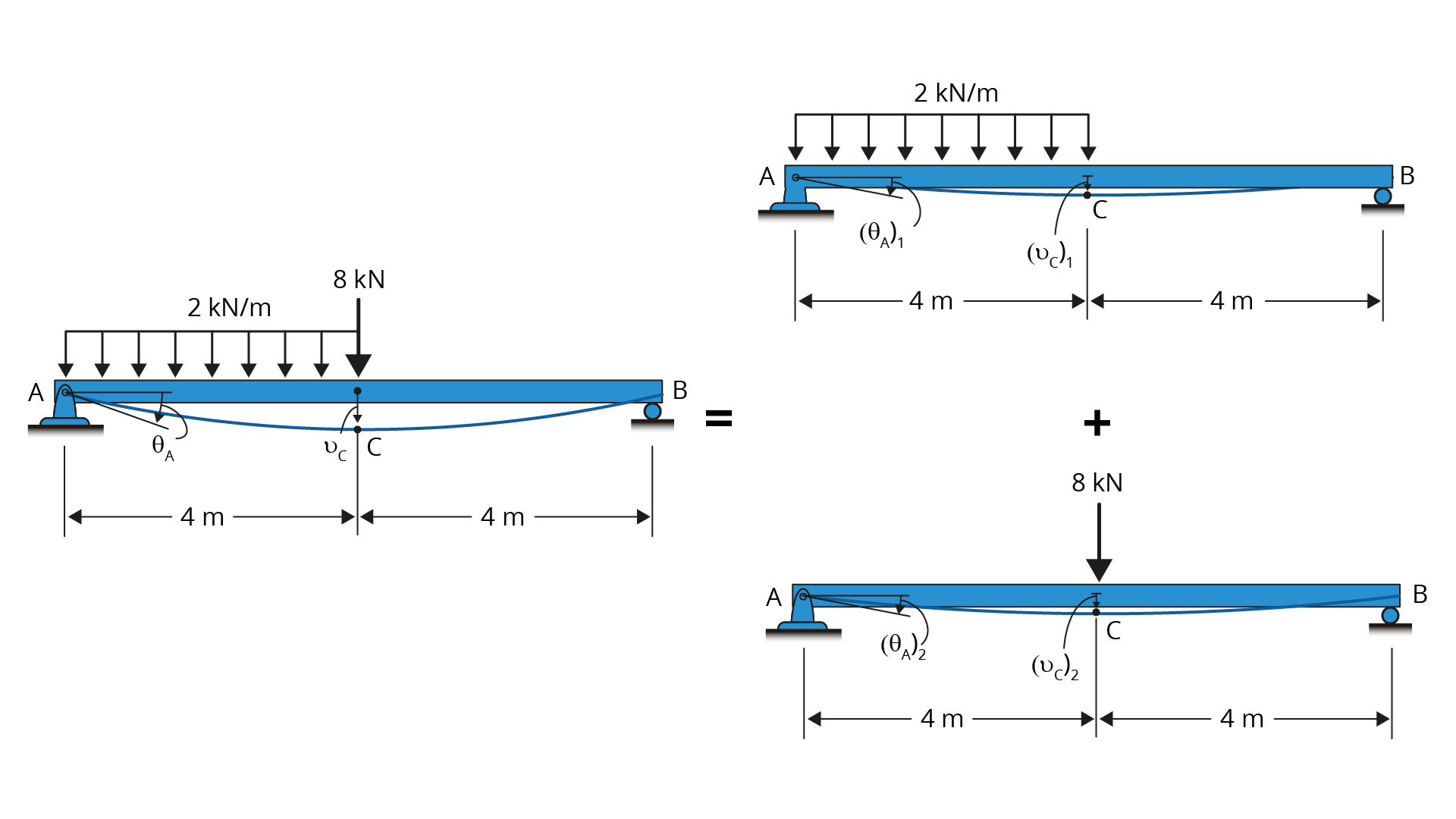
Como a figura anterior nos mostra, a viga é dividida em dois segmentos mais simples de se resolver. Esses são tabelados, podendo ser encontrados em apêndices de livros de Resistência dos Materiais. A figura a seguir traz os segmentos necessários para a resolução no nosso problema.
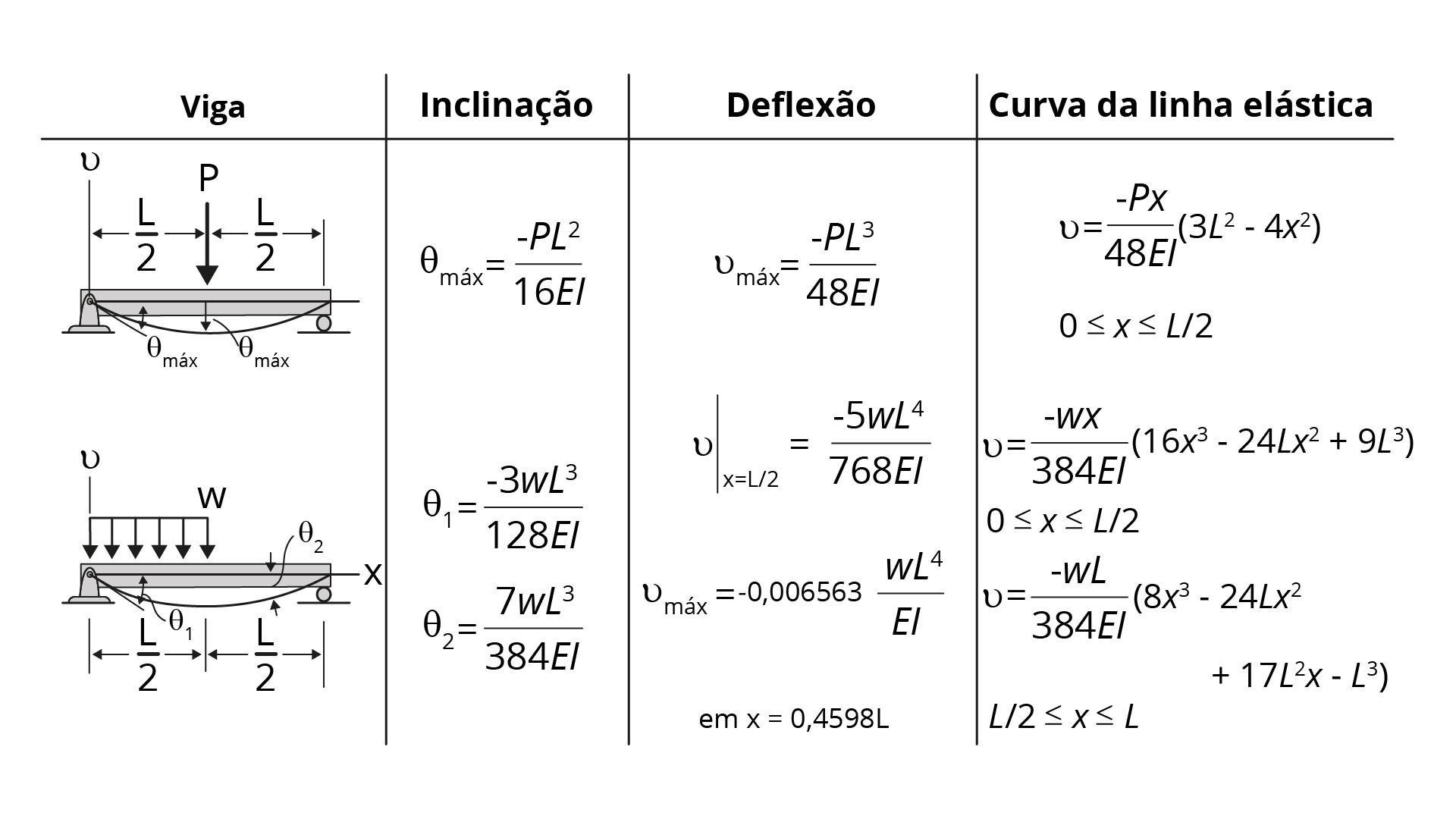
Com base nesses dados tabelados, podemos então calcular a inclinação e o deslocamento para a viga nos pontos A e C, respectivamente.
\[{{\theta }_{A}}={{\left( {{\theta }_{A}} \right)}_{1}}+{{\left( {{\theta }_{A}} \right)}_{1}}=\frac{3wL{}^\text{3}}{128EI}+\frac{PL{}^\text{2}}{16EI}=\frac{3\left( 2 \right)\left( 8 \right){}^\text{3}}{128EI}+\frac{8\left( 8 \right){}^\text{2}}{16EI}=\frac{56~kN.m{}^\text{2}}{EI}~\circlearrowright \]
\[{{v}_{c}}={{\left( {{v}_{c}} \right)}_{1}}+{{\left( {{v}_{c}} \right)}_{2}}=\frac{5w{{L}^{4}}}{768EI}+\frac{PL{}^\text{3}}{48EI}=\frac{53,33}{EI}+\frac{85,33}{EI}=\frac{139~kN.m{}^\text{3}}{EI}\downarrow \]
Só podemos aplicar esse método em vigas com pequenos deslocamentos, dentro do regime elástico.
O método da área do momento é uma abordagem alternativa para descobrir os deslocamentos de uma viga ou eixo. É baseado em dois teoremas que estão relacionados à área do diagrama de momento.
1º teorema : o ângulo, em radianos, entre as tangentes de quaisquer dois pontos na linha elástica é igual à área abaixo da curva M/EI entre esses dois pontos.
2º teorema : A distância vertical entre a tangente de um ponto na linha elástica e a tangente estendida de outro ponto é igual ao momento da área abaixo do diagrama M/EI entre esses dois pontos. Esse momento é calculado sobre o ponto onde a distância vertical deve ser determinada.
O procedimento de análise deve ser feito, seguindo a ordem:
A resolução de um problema nem sempre considera apenas números. Muitas vezes a solução analítica considera apenas variáveis e é então utilizada diversas vezes, alterando-se as incógnitas. A fim de exemplificar isso, considere a viga mostrada em (a). Com o diagrama M/EI em (b) e a linha elástica em (c).
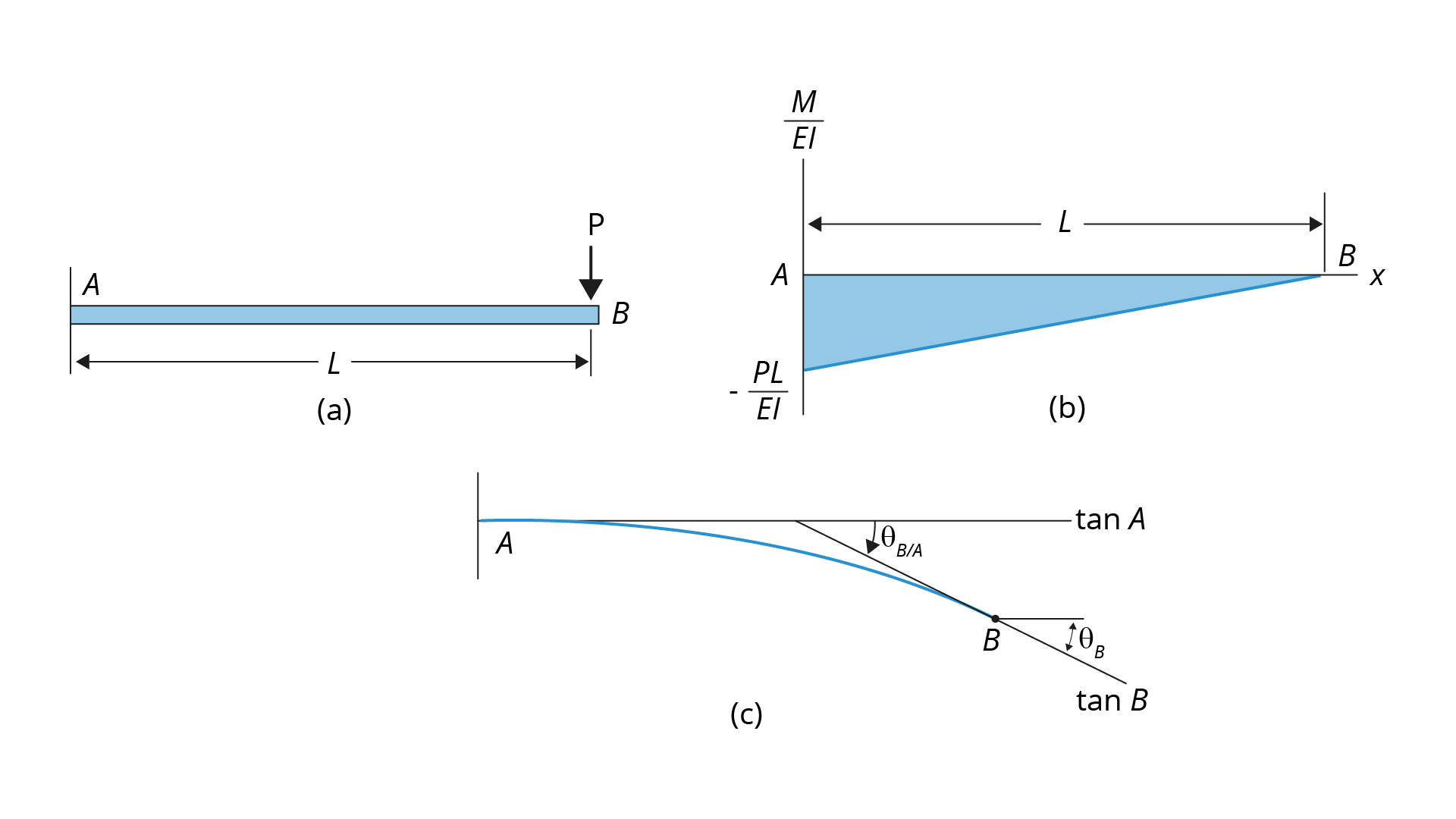
Determine sua inclinação pelo método da área.
Vigas e eixos estaticamente indeterminados possuem mais reações desconhecidas do que equações de equilíbrio. Para resolvê-los, devem-se identificar as reações redundantes. Os métodos de integração ou método dos teoremas de área do momento podem ser utilizados para resolver as incógnitas redundantes. Também se utiliza o método da superposição para determinar quais reações são redundantes.
Neste capítulo estudaremos a flambagem, que é um evento ativado por cargas axiais compressivas em colunas , que são elementos estruturais longos e esbeltos. Quando as colunas estão sendo comprimidas por essa força axial, elas podem sofrer uma deflexão lateral , que é denominada flambagem . Essa deflexão lateral pode ocasionar, em muitos casos, uma falha repentina na estrutura, sendo então de grande importância sua consideração durante o projeto de colunas.
Denomina-se
carga crítica
\((P_{cr})\) a carga axial máxima que uma coluna pode suportar, na iminência de sofrer flambagem.
A carga crítica não é a maior carga que uma coluna pode suportar, pois mesmo depois de flambada ela poderá aguentar cargas maiores que \(P_{cr}\) , porém, como consequência apresentará uma grande deflexão. Em geral, não se toleram grandes deflexões em projetos de estruturas, sendo assim, \(P_{cr}\) passa a ser a carga limite para a coluna.
O artigo Análise da fase de montagem de lajes treliçadas traz uma avaliação de lajes treliçadas, comumente utilizadas no Brasil. Entre os principais mecanismos de falha que são observados, um é a flambagem. A leitura recomendada aborda diversos tópicos da resistência dos materiais e os traz para a realidade da engenharia civil, mostrando ensaios e cálculos utilizados no dia a dia de tais avaliações.
Será considerada como coluna ideal a coluna que apresenta as características a seguir:
Na figura anterior, é apresentada uma coluna apoiada sobre pinos. Se aumentarmos a carga axial P , antes de a coluna falhar por escoamento ou ruptura, ela se encontrará na iminência de se tornar instável e sofrer flambagem ao se atingir a carga \({{P}_{cr}}\). Nesse momento, quando se aplica uma força F na lateral da coluna, a viga irá defletir e permanecerá defletida mesmo removendo a força F . Qualquer redução na carga axial P em relação a \({{P}_{cr}}\) fará com que a coluna volte à posição inicial. Qualquer aumento na carga axial P em relação a \({{P}_{cr}}\) provocará aumento da deflexão lateral da coluna.
Para se calcular a carga crítica \({{P}_{cr}}\) de uma coluna, leva-se em conta a sua rigidez à flexão, dada pela relação abaixo, entre o momento interno da coluna com sua forma defletida:
\(EI\frac{d{}^\text{2}v}{dx{}^\text{2}}=M\) (eq. 4.16)
O momento interno M é determinado pelo método das seções, com o auxílio do diagrama de corpo livre:
Sendo assim, igualando a zero a equação e reorganizando os termos:
\(\frac{d{}^\text{2}v}{dx{}^\text{2}}+\left( \frac{P}{EI} \right)v=0\) (eq. 4.17)
A equação acima é uma equação diferencial linear homogênea de segunda ordem, com coeficientes C1 e C2 constantes. A solução geral é dada por:
\(v=C1sen\left( \sqrt{\frac{P}{EI}x} \right)+C2cos\left( \sqrt{\frac{P}{EI}x} \right)\) (eq. 4.18)
Aplicando as condições de contorno na extremidade da coluna para se descobrir C1 e C2:
\(C1sen\left( \sqrt{\frac{P}{EI}x} \right)=0\) (eq. 4.19)
Essa igualdade é satisfeita se:
\(P=\frac{n{}^\text{2}\pi {}^\text{2}EI}{L{}^\text{2}}\) (eq. 4.20)
O menor valor de P é obtido com n=1 e essa carga crítica é conhecida como carga de Euler e será a fórmula utilizada para a flambagem de uma coluna apoiada por pinos:
\({{P}_{cr}}=\frac{\pi {}^\text{2}EI}{L{}^\text{2}}\) (eq. 4.21)
Onde:
● \(P_{cr}\) 🡪 carga crítica da coluna, dada em \(N\);
● \(E\) 🡪 módulo de elasticidade do material, dado em \(Pa (N/m²)\);
● \(I\) 🡪 momento de inércia de área da seção transversal, dado em \({{m}^{4}}\);
● \(L\) 🡪 comprimento da coluna, presa por pinos, dado em \(m\).
O
n
, tratado como 1 na equação 4.21, representa o número de ondas na forma defletida da coluna:
Importante observar que a carga crítica \(({{P}_{cr}})\) da coluna depende somente das suas dimensões, ou seja, do momento de inércia da área da seção transversal \((I)\) e de seu comprimento \((L)\). O módulo de elasticidade do material \((E)\) também é aplicado, porém, dentro de uma mesma categoria de materiais, aço por exemplo, quando se trata de flambagem elástica, não há vantagem em se usar um aço de alta resistência em relação a um aço de baixa resistência. Pode-se melhorar a resistência da coluna aumentando-se o momento de inércia da seção.
Outro ponto importante é o fato de que uma coluna sempre sofrerá flambagem em torno do eixo principal correspondente ao
menor momento de inércia
\((I)\), ou seja, o eixo menos resistente. Por exemplo, na imagem a seguir, a coluna retangular sofrerá flambagem em torno do eixo
a-a
. Na prática, busca-se sempre deixar os momentos de inércia em relação aos eixos principais (\({{I}_{x}}e~{{I}_{y}})~\) o mais próximo possível um do outro.
O momento de inércia da área da seção transversal da coluna também pode ser escrito como:
\(I=Ar{}^\text{2}\) (eq. 4.22)
Onde:
Substituindo a relação na fórmula da carga crítica e reorganizando os termos, obtém-se a fórmula para a tensão crítica de flambagem da coluna apoiada sobre pinos:
\({{\sigma }_{cr}}=\frac{\pi {}^\text{2}E}{\left( L/r \right){}^\text{2}}\) (eq. 4.23)
Onde:
\(r=\sqrt{I/A}\) (eq. 4.24)
A relação L/r é conhecida como índice de esbeltez da coluna e é muito utilizada na classificação das colunas em longas, intermediárias ou curtas.
Exemplo 4:
Considere um tubo redondo de aço ASTM A36 (\({{\sigma }_{e}}=250~MPa\)), com diâmetro externo de 152,4 mm, diâmetro interno de 139,8 mm e comprimento 7,31 m sendo utilizado como coluna, presa por pinos nas extremidades. Determine a carga crítica, ou seja, a carga axial máxima que a coluna suportará sem sofrer flambagem. Utilize como módulo de elasticidade do aço E = 207.000 MPa.
Solução:
Como é uma coluna apoiada sobre pinos, podemos aplicar a fórmula da carga de Euler vista:
\[{{P}_{cr}}=\frac{\pi {}^\text{2}EI}{L{}^\text{2}}\]
Inicialmente calcula-se o momento de inércia da área da seção transversal da coluna, neste caso, para um tubo redondo:
\[I~=~\frac{\pi {{({{D}^{4}}-{{d}^{4}})}_{{}}}}{64}=\frac{\pi \left( {{152,4}^{4}}-{{139,8}^{4}} \right)}{64}=7.729.615,2~m{{m}^{4}}~\]
Utilizando então a fórmula da carga de Euler, descobre-se a carga crítica para a coluna:
\[{{P}_{cr}}=\frac{\pi {}^\text{2}EI}{L{}^\text{2}}=\frac{\pi {}^\text{2}\times 207000\times 7729615,2}{7310{}^\text{2}}=295,5~kN\]
Pode-se descobrir também a tensão crítica para a coluna e comprovar que, conforme teoria, esta é menor que a tensão de escoamento do material \(({{\sigma }_{e}}=250~MPa)\):
\[{{\sigma }_{cr}}=\frac{\pi {}^\text{2}E}{\left( L/r \right){}^\text{2}}=\frac{\pi {}^\text{2}E}{\left( L/\sqrt{I/A} \right){}^\text{2}}=\frac{\pi {}^\text{2}207000}{\left[ 7310/\left( \sqrt{\frac{7729615,2}{\pi 76,2{}^\text{2}-\pi 69,9{}^\text{2}}} \right) \right]{}^\text{2}}=102,2~MPa\]
A fórmula da carga crítica mostrada anteriormente considerava a coluna apoiada por pinos, com as extremidades livres para girar. O procedimento de se obter a fórmula da carga crítica para uma coluna apoiada sobre diferentes tipos de apoio é o mesmo utilizado para a coluna apoiada sobre pinos. Frequentemente encontramos aplicações onde as colunas podem estar engastadas em uma extremidade e pinadas em outra, ou então com uma extremidade livre, por exemplo.
O que muda quando se trata de outros tipos de apoio é o comprimento da coluna (L) a ser considerado. Anteriormente o L considerado correspondia ao comprimento da coluna, ou também à distância na coluna sem os apoios, ou seja, à distância entre os pontos de momento nulo. Dependendo do tipo de apoio da coluna teremos um tipo diferente de distância L entre os pontos de momento nulo. Essa distância entre os pontos de momento nulo é chamada de comprimento efetivo \(\left( {{L}_{e}} \right)\) da coluna. Para uma coluna presa por pinos \({{L}_{e}}=L\).
Na aplicação das fórmulas da carga crítica \(({{P}_{cr}})\) para cada tipo de apoio, ao invés de se trabalhar com o comprimento efetivo \(\left( {{L}_{e}} \right)\), utiliza-se de um coeficiente adimensional K denominado fator de comprimento efetivo. A relação de K com \({{L}_{e}}\) é dada por \({{L}_{e}}=KL\).
O fator de comprimento efetivo
(K)
é tabelado e depende de cada tipo de apoio da coluna. Na sequência são mostrados casos com alguns fatores K comumente utilizados:
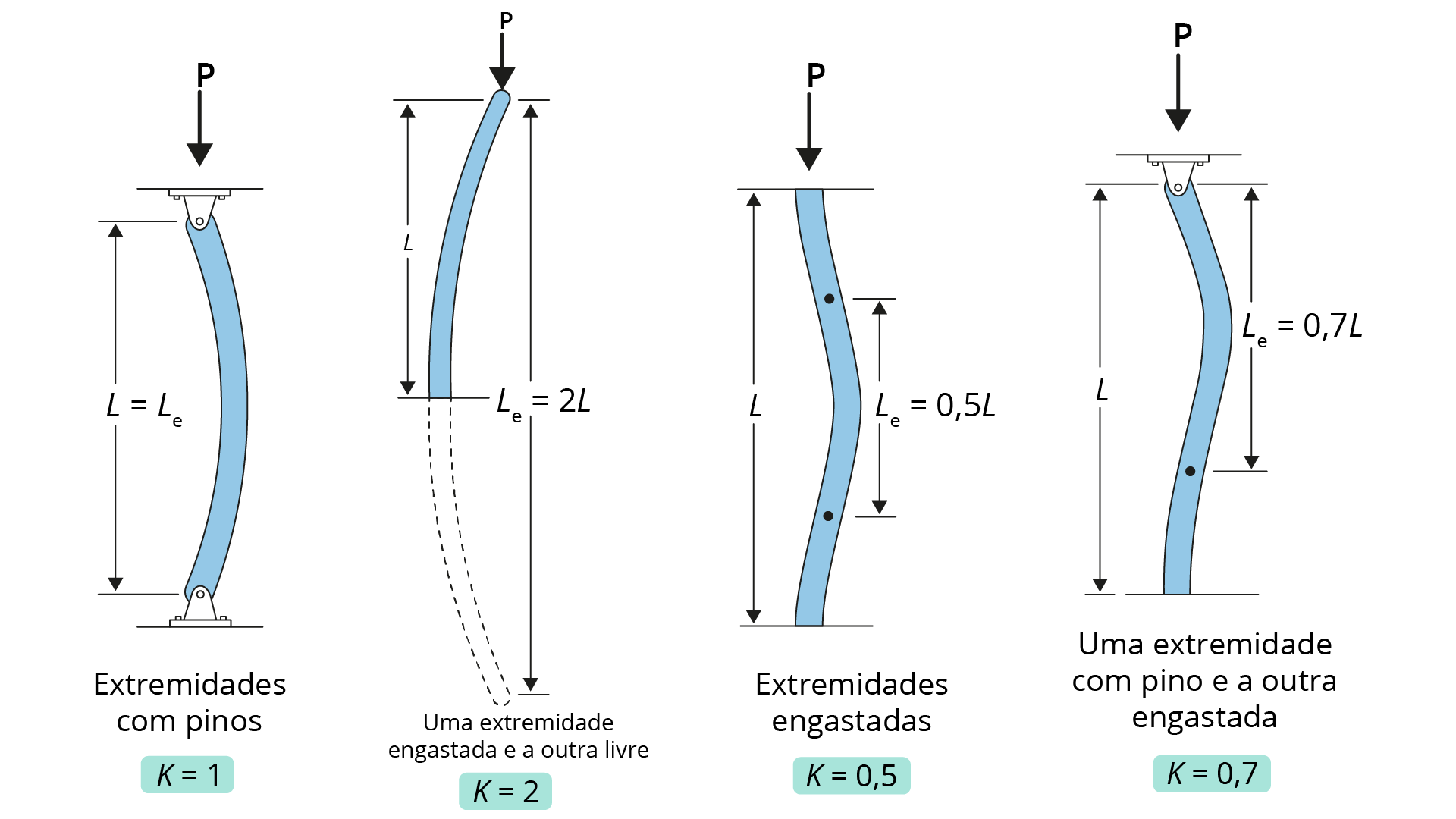
As fórmulas da carga crítica \(({{P}_{cr}})\) e da tensão crítica \(({{\sigma }_{cr}})\) para todos os casos são apresentadas abaixo, onde o fator K deve ser utilizado conforme o caso analisado:
\({{P}_{cr}}=\frac{\pi {}^\text{2}EI}{\left( K{{L}_{{}}} \right){}^\text{2}}\) (eq. 4.25) \({{\sigma }_{cr}}=\frac{\pi {}^\text{2}E}{\left( KL/r \right){}^\text{2}}\) (eq. 4.26)
Nessas novas fórmulas, o
índice de esbeltez
da coluna passa a ser representado pelo termo
(KL/r)
.
A flambagem é um problema visto em diversas situações, inclusive em materiais de pavimentação, especialmente o concreto, uma vez que o asfalto tende a ser mais flexível. A radiação solar é absorvida por esse material, que causa uma tendência de expansão. Caso a tensão seja o suficiente, pode acontecer um empilhamento do material asfáltico e sua subsequente trinca. Também se observa o efeito da flambagem em trilhos de ferrovias. Com base nisso, reflita a respeito de que propriedades um material para trilhos deve possuir, para que não falhe por flambagem dessa natureza.

Russell Hibbeler
Editora: Pearson
Capítulos: 11, 12 e 13
Comentário: Para um maior entendimento de alguns conceitos, recomenda-se a leitura dos capítulos 11,12 e 13 do livro mencionado, especialmente na parte de deflexão de vigas, onde o equacionamento pode ser um pouco mais complexo, trazendo abordagens mais analíticas, como o conceito de superposição e o método das áreas.
Ano: 2018
Comentário: Neste vídeo, uma comparação entre os tipos de víncula (engaste ou apoio) para vigas de concreto armado é feita. Aqui, o comentarista fala sobre as principais diferenças que o projetista deve considerar, com apoio de um kit mola para visualização dos esforços e como os vínculos reagem. Interessante vídeo dentro do contexto de projeto de vigas e eixos.
Prezado(a) aluno(a), inicialmente, esta unidade parece muito condensada, com muito conteúdo novo, porém, vale lembrar que muito do conteúdo aqui abordado é a aplicação de conhecimentos prévios da mecânica dos sólidos e da estática. Esse conteúdo serve como base para o projeto de vigas e eixos, que é um dos principais componentes da resistência dos materiais e, em vista de sua importância, esperamos que os tópicos aqui trazidos sirvam para que esses conhecimentos possam ser aplicados por você, de forma autônoma. Além do conteúdo supracitado, a falha por flambagem, importante mecanismo em colunas, foi aqui explicitado. Assim sendo, a abordagem analítica da resolução de problemas torna-se fundamental em problemas de projeto e é essa mentalidade que esperamos que você absorva e utilize no seu dia a dia como futuro projetista de estruturas e elementos estruturais.
GERE, James B. Mechanics of Materials : brief edition. Stamford: Cengage Learning, 2012.
HIBBELER, Russell. Resistência dos Materiais . 7. ed. São Paulo: Pearson, 2009.
HIBBELER, Russell. Mechanics of Materials . Hoboken, NJ: Pearson, 2015.
SARTORTI, A. L.; FONTES, A. C.; PINHEIRO; L. M. Análise da fase de montagem de lajes treliçadas. In: Revista Ibracon de Estruturas e Materiais , v. 6, n. 4, agosto 2013. p. 623-660. Disponível em: http://www.scielo.br/pdf/riem/v6n4/pt_08.pdf . Acesso em: 18 fev. 2020.